一题一课 举一反三*——关注“核心素养”的高考专题复习课
2016-12-12陈彬
●陈 彬
(诸暨中学 浙江诸暨 311800)
一题一课 举一反三*
——关注“核心素养”的高考专题复习课
●陈 彬
(诸暨中学 浙江诸暨 311800)
文章以二面角的专题复习为例,通过一个几何模型,经过大量变式不断变换问题情景,以问题串的形式引导学生循序渐进,在问题探究的过程中完成知识和方法的整合以及基础与能力的深化.
核心素养;能力提升;数学教育;复习课
高考复习课的基本任务是帮助学生整合已有的知识和方法,形成知识和方法系统,领会基本的数学思想.据笔者了解,“大题量、高密度、快节奏”已经成为高考复习课的基本特点,题型总结也被异化为高考复习课的基本任务.可喜的是,这种现象已经引起了广大教师的反思并在教学中加以改进.笔者认为,以“精选例题,注重变式,合理设问”为基本特点的一题一课式的复习课,对于知识和方法的整合非常有效,该做法以学生能力的提升为目标,是培养学生数学“核心素养”的有效手段.笔者以二面角专题复习课为例,展示笔者在这方面所做的一些尝试.
1 高考复习课的新范式——一题一课
笔者之所以寻求改变,源于对传统复习课的体会和思考.经过长期实践检验的传统教学模式有其合理性,在一定程度上能够使学生快速提高成绩,有实战意义,但不可否认的是,这种模式也存在着很多缺点.
1.1 传统复习课的模式与缺点
长期以来,高考复习课的基本模式是:复习基础知识→讲解基本题型和例题→练习与总结→习题操练.这种模式存在的主要问题有:
1)基础知识复习阶段以重复讲解知识点和强调易错点为主,总是在“重复昨天的故事”,学生的兴趣不大,授课效果事倍功半.
2)例题讲解阶段以题型归类为主,按照基本题型组织课堂,这样做有其合理性,具备一定的实效,但缺点也是非常明显的,首先是大量的例题割裂了方法系统的整体性,不利于学生形成知识和方法系统.
3)整个课堂容易陷入灌输式的泥潭,教师教得苦,学生学得累,经常是“讲台上老师眉飞色舞,课桌前学生昏昏欲睡”,教学效率极为低下.
1.2 “一题一课”模式的基本认识
为了克服上述缺点,笔者解决问题的基本策略是:
1)精简例题,争取做到“一课一题”,通过巧妙的变式练习,让学生在变式教学的过程中体会各种方法,明辨各类方式方法的思想实质及知识间的联系,从而形成知识系统;
2)打破传统的教学模式,将知识复习贯穿于例题教学中,通过解决问题达到回顾知识的目的;
3)以问题串的形式引导学生分析问题、解决问题,增强学生的参与度,提高教学的效率.
2 “一题一课”之例——二面角复习课
二面角是立体几何的重要知识和重要考点.笔者以正方体为基础模型和题根,通过变式设问,形成问题串,通过对问题串的探究和解答,回顾了二面角的平面角、二面角的平面角的常见作法、求二面角的基本方法等知识点,通过一个数学模型的不断变化,梳理了知识之间的联系,形成了知识系统.
2.1 二面角的平面角的概念复习
设问1 二面角的大小通过二面角的平面角来刻画,这是立体几何问题平面化的策略,那么,什么是二面角的平面角呢?通过如下的问题来回答:
1)请在如图1所示的正方体中,找出二面角A1-AB-D的平面角.
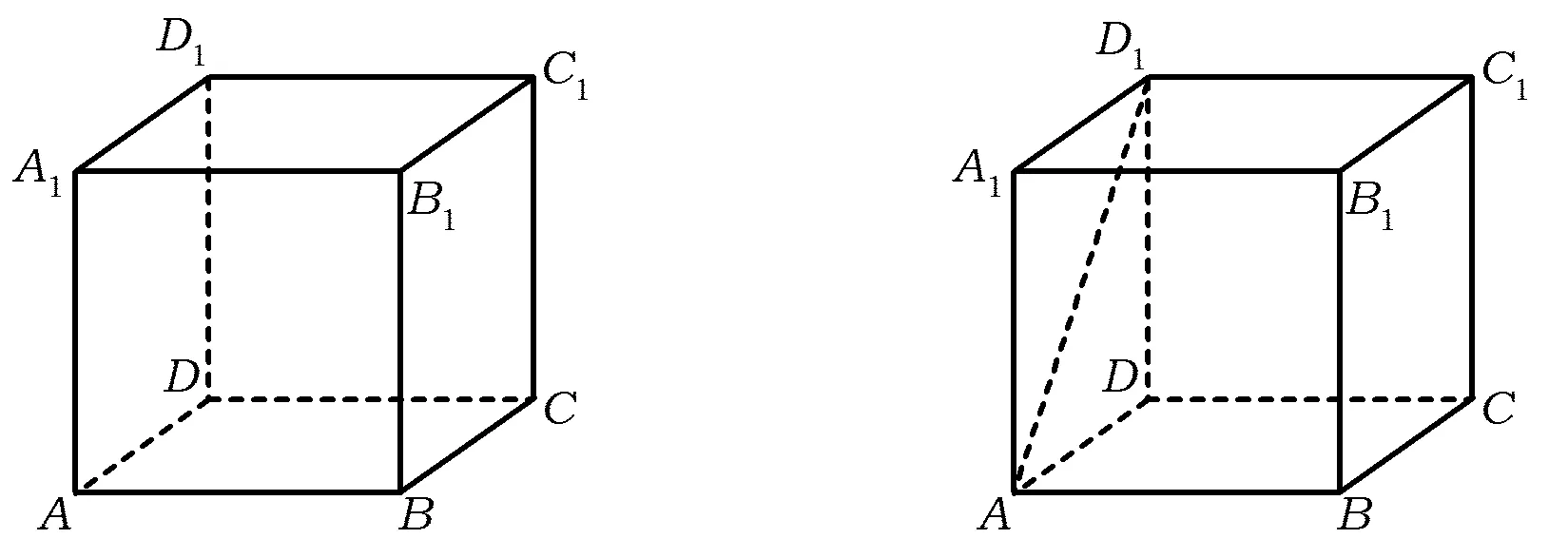
图1 图2
2)如图2,换成求二面角D1-AB-D的平面角呢?
3)如图3,再换成二面角D1-AC-D呢?根据前2个小题,该平面角是否就是现成的∠D1AD或∠D1CD呢?

图3 图4
2.2 二面角的平面角的作法
设问2 在没有现成平面角的情况下,如何作出二面角的平面角?
1)如何作二面角D1-AC-D的平面角?
2)如图4,若F是棱CD的中点,请作出二面角D1-AF-D的平面角.是否依旧只要取棱AF的中点再联结呢?
3)共棱AF的△DAF与△D1AF并非特殊的等腰三角形,那该怎么办呢?
设计意图 问题1)~3)的连续设置,通过转换问题情景,引导学生明确作二面角平面角的一般思路:寻找“现成的二面角”→通过“巧合点”(如同底的等腰三角形底边的中点)利用定义作出平面角→利用三垂线定理通过作“三垂线”作出二面角的平面角.通过设问巩固了求二面角的常用方法:定义法和三垂线法.以问题2)为例,该设问使学生意识到三垂线法作二面角的平面角的关键是找出或作出半平面的垂线.
4)如图5,若F是棱BB1的中点,请作出二面角C1-AF-B的平面角.
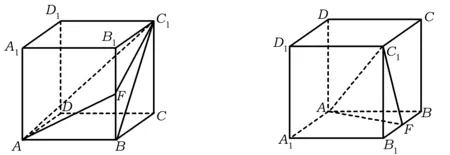
图5 图6
5)在如图6所示的正方体中,若F是棱BB1的中点,请作出二面角C1-AF-B的平面角.
通过师生、生生的互动交流,问题得以解决.
师:这就表明适时调整几何体的位置可简化问题.那么按照刚才的操作(如图7),是否可以确定∠C1GB1就是所求的角呢?
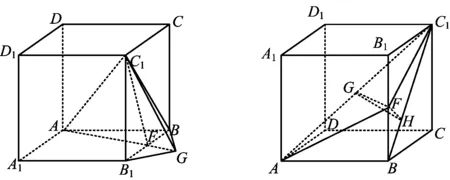
图7 图8
生:不是,应该是它的补角.
师:由此发现用三垂线法解决问题时只能求锐二面角,若要求钝二面角,就先求它的补角.
6)若更换4个顶点的顺序,则二面角就发生了相应的变化,当把“二面角C1-AF-B”改为“二面角F-AC1-B”时(如图8),请作出对应的平面角.
师:能否尝试过点B作公共棱的垂线呢?
生:过点B作BK⊥AC1于点K,再作KL⊥AC1交AF于点L,联结BL(如图9),则∠BKL即为所求角.

图9 图10
师:以上都是结合定义直接作出二面角,再构造三角形,利用余弦定理求解.同学们能否尝试找找面的垂线呢?
生:取BC中点G(如图10),联结FG,可证得FG⊥BC1,因为AB⊥面BC1,所以AB⊥FG,则FG⊥面ABC1,即FG为面ABC1的垂线.
师:怎么证明FG⊥BC1呢?
生:可通过△FBG∽△BB1C1来证明.
生:也可联结B1C.因为FG是△BCB1的中位线,所以FG∥B1C.又因为在正方形BCC1B1中,B1C⊥BC1,所以FG⊥BC1.
师:请作出该平面角.
生:记FG与BC1的交点为I,过点I作IT⊥AC1于点T,再联结FT(如图10),则∠FTI即为所求角.
7)若直接过点F作面ABC1的垂线有困难,则该怎么办?
通过师生、生生的对话,问题再次得以解决.
师:由此发现,若现成的线面垂直不好找,也可利用图形特征转化为找其他相关的线面垂直,或找面面垂直,再利用其性质定理转化为线面垂直.
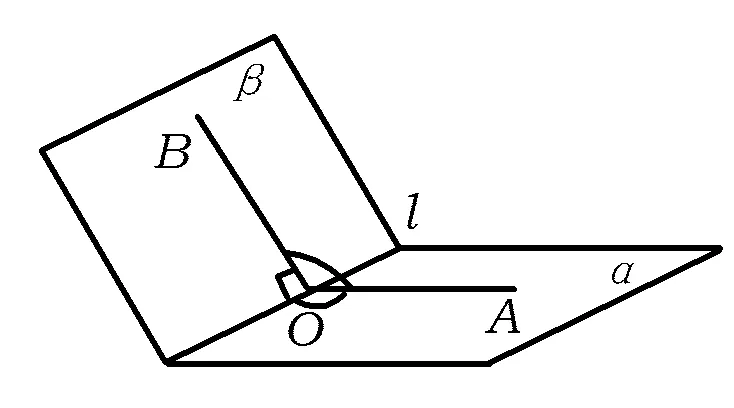
图11
8)如图11,结合二面角平面角的定义,在棱l上找一点O引2条射线OA,OB与棱l垂直(相当于棱垂直于2条射线确定的平面).换句话说,要找平面角也可以找棱的一个垂面与2个半平面的交线(2条射线)所成的角.能否试着去找棱AC1的垂面呢?
设计意图 问题4)和问题5)的设计目的是当“面的垂线”不容易作出时,可适时调整几何体的位置从而使问题转化为“熟悉的模型”.而问题6)和问题7)的设计目的是增强学生在作面的垂线时的灵活性.问题8)的设计意在使学生意识到作二面角的平面角,实际上是构造了一个棱的“垂面”,从而引出垂面法.
通过以上变式的探讨,逐一复习了二面角平面角的几种常见的作法:定义法、三垂线法、垂面法等.接下来,笔者继续进行变式,将求二面角的一些特殊情况加以展现:
设问3 如图12,若F是棱CC1的中点,请作出平面D1AF与平面ABCD所成的锐二面角的平面角.请观察该题与前面的设问1、设问2有什么区别?

图12 图13
生:没有现成的交线.
师:如何找到2个面的交线呢?
生:延长D1F,DC交于点E,联结AE即为交线.过点D作DG⊥AE于点G,联结D1G,则∠D1GD即为所求角.
师:面对无棱二面角,尽可能去作出棱,若作不出呢?譬如说如何求锐二面角的平面角的余弦值?
生:用射影法.因为点D1,F在面ABCD内的投影点分别为点D,C,则△DAC是△D1AF在面ABCD内的射影三角形.

生:向量法.
设计意图 设问3给学生展现了求二面角的一些特殊情况,当二面角的棱没有作出时,应当先作出棱再求解,若作棱有困难,则可直接用射影法和向量法.这样不仅使学生复习巩固了求二面角的基本方法,而且将各种方法灵活应用.
2.3 课堂小结
课堂小结部分,笔者也采用问题的形式进行:
设问4 通过本堂课的学习,你有怎样的收获呢?
通过师生的互动交流,本节课的收获如下:
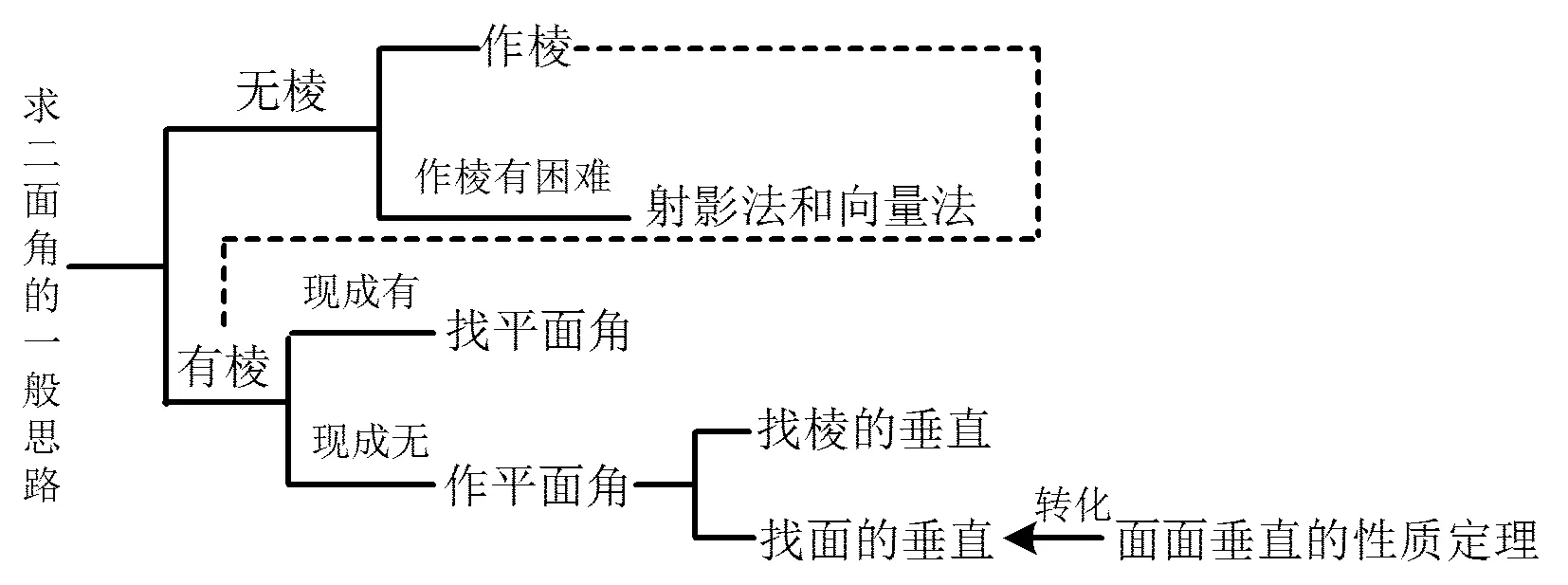
首先,师生一起巩固了求二面角的常用方法有:定义法、垂面法、三垂线法.若作角有困难,也可尝试用射影法或向量法.其次,明确了求二面角的一般思路:
1)应当先找平面角,若找不到,就作平面角.通过例题我们体会到找平面角实际就是作棱的垂面,最有利的情形是找棱的垂面或面的垂线,若没有,则根据面面垂直的性质定理,在一个面内作交线的垂线跟另一平面垂直.
2)若所求二面角没有画出棱,则可先作出棱再求解,若作棱有困难,则可直接用射影法和向量法.
3 几点反思
上述教学过程的成功促使笔者展开了思索:是什么原因使得我们获得更好的效果呢?
3.1 “一题一课”式复习课教学模式有利于学生形成知识与方法系统
以“精选例题,注重变式,合理设问”为基本特点的一题一课式的复习课教学,打破了碎片化知识点为中心的灌输式教学,整个探究过程对知识和方法的整合非常有效.本课例从最初的引导学生“寻找现成的二面角”本身,过渡到“找不到现成的二面角”就转移到“作二面角”,再亲身经历“作二面角”的种种难处,直到抓住构造二面角的本质——找棱的垂面或面的垂线.通过一系列问题串的设计,不断激起学生思维的冲突,让学生在变式过程中学会基本方法,体会方法间的联系,这为发挥学生的主体能动性创造了良好的条件.
3.2 “一题一课”式复习课成功的关键是母题的选择以及问题情景的转换
本课例以正方体为基础模型和题根,着眼于在学生认知水平的“最近发展区”内设置母题,这为发挥学生的主体能动性创造了良好的条件.随着对母题的深入研究,产生了鲜活的新问题,并始终依托正方体这个模型,通过不断更换中点的位置,为学生呈现了求二面角的各种情形,通过问题串架构起知识的脉络,使得复习课不再拘泥于就题论题,而是就题及类,连题成面,逐步实现“一题多变,一题多解,一法多用”的变化模式,从真正意义上既复习知识,学会方法,领会思想,又“活跃”课堂.
3.3 问题情景的转换过程中应当鼓励学生参与“变式活动”
在本课例中,教师不断转换问题的情景,使得学生灵活掌握求二面角的各种方法,并了解各种方法适用的情形.但是,通过反思,笔者认为在本节课的教学过程中还需要改进以下3个方面:
1)最突出的是问题情景的转换均在教师的掌控之下,使得教学活动完全按照教师的“预设”进行,缺少精彩的生成.如果在变式的过程中,能够引导学生参与变式、拟题活动,提出一些有探究价值的问题,一定会使本节课添彩不少.
2)本节课在注重思想与方法引导的同时,对计算能力的考查未能深入涉及.从课后的作业完成情况来看,思路准确性极高,但计算能力有待提高.
3)在教学过程中,学生的极高参与度造就了课堂的高密度,但有个别学生未能适应这种高容量课堂,课堂上偶有困惑神情,教学过程中期待适时“慢”节奏,有助于加深学生对知识的理解和掌握.
�2016-05-31;
2016-09-10
陈 彬(1983-),女,浙江诸暨人,中学一级教师.研究方向:数学教育.
O123.2
A
1003-6407(2016)12-07-04
