端框移动平台双驱同步控制系统设计

费少华 ,刘 丹 ,乔明杰,章 明,方 强

(1. 浙江大学 浙江省先进制造技术重点研究实验室, 浙江 杭州 310027; 2. 西安飞机工业(集团)有限责任公司,陕西 西安 710089)



端框移动平台双驱同步控制系统设计

费少华1,刘 丹1,乔明杰2,章 明1,方 强1

(1. 浙江大学 浙江省先进制造技术重点研究实验室, 浙江 杭州 310027; 2. 西安飞机工业(集团)有限责任公司,陕西 西安 710089)

在某型飞机数字化装配系统中,为了解决大尺寸、大负载端框移动平台两轴驱动位置不同步问题, 将交叉耦合技术引入自适应控制, 提出自适应耦合同步控制策略. 建立端框移动平台双驱机构的非线性数学模型; 设计端框移动平台的自适应耦合同步控制算法以及自适应律, 根据李雅普诺夫稳定性定理、Barbalat引理及LaSalle引理证明系统的稳定性和收敛性; 完成基于自适应耦合同步控制的双轴闭环控制系统设计, 在保证单轴跟踪精度的同时实现双轴同步控制. 实验结果表明, 基于自适应耦合同步控制的端框移动平台位置跟踪误差小于0.040 mm, 位置同步误差最大值为0.011 mm．

端框; 端框移动平台; 自适应耦合控制; 同步控制; 位置同步误差

飞机装配是飞机制造过程中最重要的环节[1], 目前的数字化装配技术已经在国内外航空制造业得到了广泛的研究和应用[2]. 在某型飞机中机身段装配中, 按照工艺要求,将前后端框作为壁板装配定位的基准. 由于机身段部件尺寸大、端框平板平面度要求高, 常常采用典型的龙门式框架结构作为端框平板的支架, 带动端框平板前后平移, 实现端框平板的精确定位. 该移动平台是装配系统的核心部件之一, 是实现机身段端框准确定位和预防机身端面变形的关键.端框移动平台的定位精度直接关系飞机部件的装配精度, 因此本文对端框移动平台的运动控制展开研究.

在实际装配过程中, 若采用单台电机驱动端框移动平台,驱动电机以及滚珠丝杠势必安装在靠近一侧导轨的内侧, 驱动力难以作用于端框移动平台的重心, 平台运动时将产生不对称的惯性力, 会对系统加减速和定位性能产生较大的影响, 甚至产生振动、变形和倾斜等情况. 端框平台采用双边驱动形式, 不仅克服了上述缺点, 还具有推力大、刚性高等优点. 当双轴同步驱动端框移动平台时, 由于端框定位系统的结构不是严格对称的, 尽管两驱动轴传动机构完全相同, 且用同一种控制方法, 但是由于两轴参数存在差异,系统模型经常发生非线性时变; 另外,受负载不均衡、外界干扰、两轴间的机械耦合等不确定因素的影响, 两驱动轴间不可避免地出现位置不同步的问题. 同时,系统承载较大, 精度要求较高, 使得实现两轴位置同步更加困难. 因此需要寻找一种有效的同步控制策略, 以满足系统大负载、高精度要求.

在同步控制方面, 国内外研究的热点是交叉耦合控制理论[3-4]. 上世纪80年代初, Koren[5]首次提出交叉耦合的控制方法, 通过附加速度差或位置差的反馈信号实现对轴间位置偏差的协调、补偿, 从而获得较好的轴间同步性能. 此后, 经过众多学者研究发现, 将自适应控制引入交叉耦合控制器中是一种有效的解决同步控制问题的途径[6]. Tomizuka等[7]基于两直流电机并行驱动结构, 设计和应用了自适应扰动补偿和自适应前馈控制技术.仿真结果表明, 运用该控制技术使速度同步误差从0.5 rad/s减小至0.3 rad/s.Sun[8]将自适应前馈控制技术进一步扩展应用到位置同步控制中, 研究发现系统的同步位置偏差可以快速地收敛为零, 但当系统负载较大或系统参数具有较大非线性时, 控制效果不佳.Sun等[9-12]研究提出自适应耦合控制策略, 将位置反馈和同步偏差反馈一起引入到控制器和参数适配器上, 实现了两机器人的协同控制.

本文以端框移动平台为研究对象, 将交叉耦合技术引入自适应控制, 设计自适应耦合双轴同步控制系统.在保证端框移动平台单轴跟踪精度的同时,实现双轴的同步运动控制.

1 端框定位装置同步控制原理

端框定位装置如图1所示, 由基座、移动平台、端框等组成, 其中移动平台呈龙门式横跨在基座上, 双边分别由两台伺服电机驱动. 驱动原理如图2所示. 在伺服电机驱动下, 通过减速器、联轴器、丝杠和螺母座的运动传递, 并由各自绝对光栅提供位置反馈, 构成两套位置闭环, 共同驱动端框定位装置的移动平台.

图1 端框定位装置示意图Fig.1 Schematic diagram of end-frame location equipment

图2 端框移动平台驱动原理图Fig.2 Schematic diagram of dual-drive of end-frame executed platform

当端框移动平台沿飞机航向运动时, 若驱动端框移动平台的两轴位置进给不同步, 由于双边存在机械耦合, 将无法达到给定的速度和加速度, 且导致端框及端框移动平台发生扭斜, 严重时甚至可能引起机械损毁. 对端框移动平台的控制不仅是单个驱动轴的控制问题, 端框两侧运动机构的精确同步运动也尤为重要.

研究双轴同步控制,须关注以下2个指标：位置同步误差和位置跟踪误差.这2个指标作为双轴位置伺服控制系统同步控制性能的指标.设计同步控制系统的最终目的是使上述2个指标尽可能快地收敛为零.定义第i(i=1, 2)轴的位置跟踪误差ei(t)为

(1)

在实际的装配过程中, 要求两轴运动的位移大小和方向均相同, 所以位置同步比例系数为a=1. 为了保证两轴同步运行, 要求在ei(t)→0的同时, 使

e1(t)=e2(t).

(2)

定义位置同步误差:

ε(t)=e1(t)-e2(t).

(3)

若ε(t)=0, 则可以实现系统性能指标(2). 根据上述位置跟踪误差和位置同步误差的定义, 双驱同步控制的问题可以描述如下: 设计控制器, 使ei(t)和ε(t)收敛趋于0.

2 自适应耦合同步控制算法设计

2.1 模型端框移动平台动力学建模

端框移动平台两运动轴均选用Kollmorgen公司的AKM33E型伺服电机, 是一款无刷直流电机,可以称之为梯形波永磁同步电机. 采用d-q轴模型对其永磁同步电机进行建模,q轴的电压方程可以表示为

(4)

式中:ui、Iqi分别为第i(i=1, 2)个电机q轴电压和电流；Li、Ri为定子每相绕组的等效电感和电阻；Kφi为反电动势常数；ωi为转子角速度.

根据牛顿第二定律, 运动方程列为

(5)

(6)

Tei=IqiKfi.

(7)式中:Ji为转动惯量；Bi为黏滞摩擦系数；Kfi为电磁转矩系数；Tei为电机输出转矩；Tfi为摩擦力矩；Tk是因机械耦合而产生的力矩, 称为机械耦合力矩.

减速器的传递函数可以看作比例环节, 即

(8)

式中:j为减速器减速比.

减速器的旋转运动经丝杠, 螺母座转化为端框移动平台的直线运动, 平台位移与减速器的累积输出有关, 因而将减速器其视为积分环节, 传递函数为

(9)

式中:l0为滚珠丝杠导程.

简化的双轴同步驱动系统的传递函数框图如图3所示.

图3 端框移动平台双驱系统模型Fig.3 Dual-drive system model of end-frame excuted platform

考虑到电枢电感较小, 忽略LidIqi/dt项的影响, 可得系统的状态方程为

(10)

(11)

2.2 耦合位置误差

考虑双轴运动控制系统, 由式(10)、(11), 将第i轴的动态特性描述如下：

(12)

(13)

(14)

式中:β是一个大于0的耦合系数, 可以用于权衡控制系统的跟踪性能和同步性能；τ为时间变量.

2.3 自适应耦合同步控制算法设计

2.3.1 控制函数定义 定义控制函数ci(t), 使

(15)

式中:

(16)

2.3.2 自适应耦合控制律设计 设计控制器的输出,即给定输入电压. 输入电压ui定义为

(17)

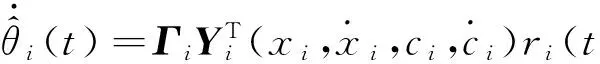
(18)

式中: Γi为自适应增益矩阵, 表征自适应速率, 为对称的正常数矩阵. 定义模型估计误差：

(19)

自适应律可以被改写成另一种形式:

(20)

2.3.4 闭环动态模型 将控制器(17)代入系统动力学模型(12),可得闭环动态模型:

(21)

2.4 自适应耦合控制算法的收敛性和稳定性研究

收敛性是判断一种控制算法能否获取优良控制性能的基础, 稳定性是系统正常运行的前提. 本文在2.3节中假定了模型参数估计的自适应律, 接下来根据李雅普诺夫稳定性理论调整并证明其正确性.

定理: 对于式(12)～(21)所设计的自适应耦合控制器, 两轴运动控制系统是稳定的, 并保证跟踪误差和位置同步误差渐进收敛为零, 即当时间t→∞时,ei(t)→0和ε(t)→0.

(22)

对V(t)关于时间t求导, 可得

(23)

将式(21)两边同时乘以ri(t), 可得

(24)

将式(24)代入式(23),可得

(25)

根据式(20)可得

(26)

由式(15)可得

(27)

将式(14)、(3)代入式(27),并整理可得

r1(t)-r2(t)=

(28)

将式(26)、(28)代入式(25),可得

(29)

(30)

将式(2)代入式(30),可得

e1(t)=e2(t)=0.

(31)

本文提出自适应耦合同步控制器, 控制器框图如图4所示. 与传统的非同步控制器相比, 优点是在两轴间建立了耦合关系, 实现了两轴协调运动. 换言之, 采用该同步控制算法不仅使e1(t)、e2(t)收敛为0, 同时两轴的同步误差ε(t)也收敛为0. 尽管两轴独立控制, 没有耦合关系时,可以使e1(t)→0,e2(t)→0, 最终ε(t)→0, 但是不能保证系统的瞬态同步性能.

3 双轴同步控制实验

自适应耦合同步控制策略最终在端框移动平台上实现.根据实际端框移动平台结构, 搭建两轴运动实验系统,验证自适应耦合控制策略的同步控制性能.

3.1 双驱同步实验系统

双驱同步实验系统如图5所示.两台型号一致的伺服电机(科尔摩根AKM系列)呈面对面安装, 两者之间装有旋转编码器, 用于反馈两电机的位置同步误差, 另外配有数字式驱动器、运动控制器和工业控制计算机等. 软件系统包括Danaher公司的Motion Console和MechaWare工具包等. 通过MechaWare工具包将自适应耦合控制算法加载到ZMP运动控制器, 从而进行系统测试.

3.2 控制器参数确定

基于自适应耦合控制算法设计的伺服控制系统的相关参数包括单轴运动的控制系数Λ、kr、自适应增益矩阵Γi以及两轴的耦合系数β、kε等.

首先确定自适应增益矩阵Γi, 矩阵Γi为对称的正定正常数矩阵, 故假设

(32)

(35)

图4 自适应耦合控制器框图Fig.4 Block diagram of adaptive coupling controller

图5 两轴同步控制实验平台Fig.5 Experimental platform of biaxial synchronous motion control

矩阵, 即

(36)

经过实验调试, 确定了矩阵Γi的对角元素值:

控制器参数值如表1所示.

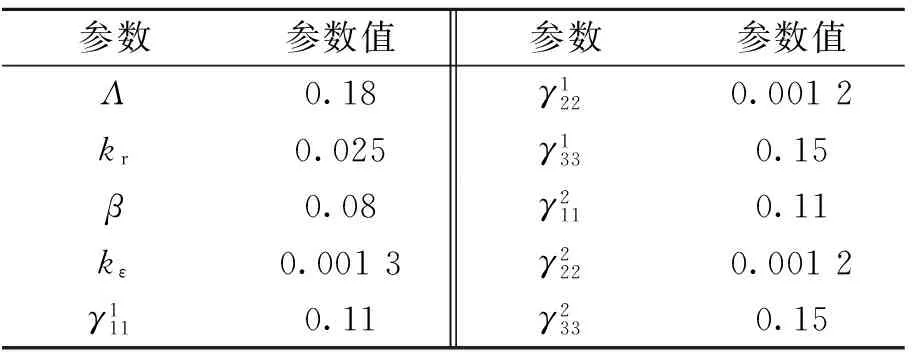
表1 自适应耦合控制器参数

3.3 实验设计与结果分析

根据端框定位装置对移动平台双驱同步控制系统的性能要求, 两轴的动态位置同步误差不超过0.020 mm, 单轴的跟踪误差上限为0.050 mm.

已知电机的旋转运动传递给减速比为3∶ 1的减速器, 然后减速器的旋转运动经导程为10 mm的滚珠丝杠转化为端框移动平台的直线运动, 可以计算出2台电机的动态位置同步误差不超过0.037 rad,单个电机的跟踪误差不超过0.094 rad.

为了验证设计的同步算法的性能, 实验选取了2种伺服信号: 频率为20 Hz、幅值为0.8 rad的正弦信号和转速为1 000 r/min、角加速度为104.5 rad/s2的斜坡信号, 分别在频率较高和转速较大2种情况下考察系统的同步控制性能.

图6 指令位置与实际位置Fig.6 Command position and actual position of two motors

图7 位置跟踪误差(正弦波指令)Fig.7 Position tracking errors of two motors with sinusoidal signal

图8 位置同步误差(正弦波指令)Fig.8 Position synchronization error with sinusoidal signal

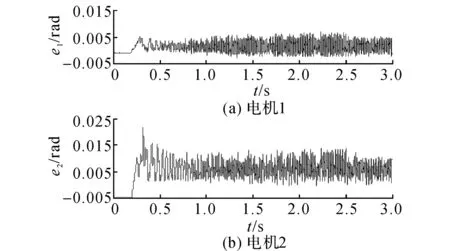
图9 位置跟踪误差(斜坡信号指令)Fig.9 Position tracking errors of two motors with ramp signal

图10 位置同步误差(斜坡信号指令)Fig.10 Position synchronization error with ramp signal

如图6～8所示为当伺服信号频率为20 Hz，幅值为0.8 rad时系统的响应情况. 图6、7反映了2台电机的位置跟踪情况.图中，t为时间,p1、p2表示两个电机的位置,xd、x分别表示电机的指令位置和实际位置,e为位置误差.整个运动过程的动态误差不超过0.050 rad, 也无明显的相位滞后. 观察图8可知, 两电机的位置同步误差始终小于0.003 rad. 如图9、10所示为当两电机转速为1 000 r/min, 角加速度为104.5 rad/s2时的跟踪误差和同步误差. 电机1的位置误差小于0.010 rad, 电机2小于0.025 rad, 两电机的位置同步误差在±0.014 rad的范围内波动. 2组实验充分证明了基于耦合位置误差的自适应耦合同步控制策略的有效性.

4 端框移动平台自适应耦合同步控制

图11 端框定位装置Fig.11 End-frame location equipment

实际的端框定位装置如图11所示, 主要由2台基座、整体式移动滑台以及直径约为5 m的端框组成. 2套基座与滑台之间各有1套基于位置反馈的闭环控制系统. 当端框以3 mm/s的速度、0.75 mm/s2的加速度运动时, 两轴的位置跟踪误差均小于0.040 mm, 如图12所示. 图13反映了两轴的同步控制效果, 同步误差最大值是0.011 mm, 满足设计要求.

图12 端框移动平台单轴位置跟踪误差Fig.12 Position tracking errors of platform’s motion axes

图13 端框移动平台两轴位置同步误差Fig.13 Position synchronization error between two axes of platform

5 结 论

(1) 建立端框移动平台双轴同步驱动系统动力学模型, 设计了端框移动平台的自适应耦合同步控制算法以及自适应律, 证明了系统的稳定性和收敛性.

(2) 通过实验验证了提出的控制系统.在跟踪频率为20 Hz、幅值为0.8 rad的正弦信号和角加速度为1 000 r/min、角加速度为104.5 rad/s2的斜坡信号下, 两电机的位置跟踪误差在±0.050 rad内, 同步误差小于0.014 rad.实验结果表明了自适应耦合控制算法的有效性.

(3) 将提出的自适应耦合控制算法应用于实际端框移动平台运动控制系统设计.当端框移动平台以3 mm/s的速度、0.75 mm/s2的加速度运动时, 基于自适应耦合同步控制的移动平台位置跟踪误差小于0.040 mm, 位置同步误差最大值为0.011 mm, 满足设计需求.

[1] 邹冀华, 刘志存, 范玉青. 大型飞机部件数字化对接装配技术研究[J]. 计算机集成制造系统, 2007, 13(7): 1367-1373． ZOU Ji-hua, LIU Zhi-cun, FAN Yu-qing. Large-size airplane parts digital assembly technology [J]. Computer Integrated Manufacturing Systems, 2007, 13(7): 1367-1373．

[2] 许国康.大型飞机自动化装配技术[J]. 航空学报, 2008, 29(3): 734-740． XU Guo-kang. Automatic assembly technology for large aircraft [J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 734-740．

[3] LIN F J, CHOU P H, CHEN C S, et al. DSP-based cross-coupled synchronous control for dual linear motors via intelligent complementary sliding mode control [J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1061-1073．

[4] LI Cong, YAO Bin, ZHU Xiong-cong, et al. Adaptive robust synchronous control with dynamic thrust allocation of dual drive gantry stage [C] ∥ASME International Conference on Advanced Intelligent Mechatronics. Besancon: IEEE, 2014: 316-321．

[5] KOREN Y. Cross-coupled biaxial computer control for manufacturing systems [J]. Journal of Dynamic Systems Measurement and Control, 1980, 102(4): 265-272．

[6] TEO C S, TAN K K, LIM S Y, et al. Dynamic modeling and adaptive control of a H-type gantry stage [J]. Mechatronics, 2007, 17(7): 361-367.

[7] TOMIZUKA M, HU J. Synchronization of two motion control axes under adaptive feedforward control [J]. Journal of Dynamic Systems, Measurement and Control, 1992, 114(2): 196-203．

[8] SUN Dong. Adaptive coupling control of two working operations in CNC integrated machines [J]. Journal of Dynamic Systems, Measurement and Control, 2003, 125(4): 662-665．

[9] SUN Dong, MILLS J K. Adaptive synchronized control for coordination of two robot manipulators [C]∥Proceedings of the 2002 IEEE International Conference on Robotics and Automation. Washington: IEEE, 2002: 976-981．

[10] SUN Dong. Position synchronization of multiple motion axes with adaptive coupling control [J]. Automatic, 2003, 39(3): 997-1005．

[11] SUN Dong, SHAO Xiao-yin, FENG Geng. A model-free cross-coupled control for position synchronization of multi-axis motions: theory and experiments [J]. IEEE Transaction on Control Systems Technology, 2007, 15(2): 306-314．

[12] SUN Dong, LU R, MILLS J K, et al. Synchronous tracking control of parallel manipulators using cross-coupling approach [J]. The International Journal of Robotics Research, 2006, 25(11): 1137-1147．

Synchronous control system design of dual-drive end-frame executed platform

FEI Shao-hua1, LIU Dan1, QIAO Ming-jie2, ZHANG Ming1，FANG Qiang1

(1.KeyLaboratoryofAdvancedManufacturingTechnologyofZhejiangProvince,ZhejiangUniversity,Hangzhou310027,China; 2.AVICXi’anAircraftIndustry(Group)LimitedCompany,Xi’an710089,China)

The synchronization control strategy of adaptive coupling was presented by incorporating cross-coupling technology into adaptive control architecture in order to solve the problem that the end-frame’s two axes with high precision and large load can’t synchronously move in the aircraft digital assembly system. The nonlinear model of dual-drive mechanism of the end-frame executed platform was conducted. The adaptive coupling control algorithm and adaptive law for end-frame executed platform were designed. Then the stability and convergence of the control system were analyzed by Lyapunov, Barbalat and LaSalle theory. A biaxial closed loop servo system was finished based on adaptive coupling synchronous control. Then the biaxial synchronous control was achieved under the high tracking accuracy of each axis. Experiments on end-frame executed platform indicate that the tracking error of two axes is below 0.040 mm, and the maximum synchronization error is 0.011 mm.

end-frame; end-frame executed platform; adaptive coupling control; synchronous control; position synchronization error

2014-12-04. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

中央高校基本科研业务费专项资金资助项目(2015FZA4005).

费少华(1986 -), 男, 助理研究员, 从事伺服控制技术的研究. ORCID: 0000-0002-2045-8831. E-mail: f307110@163.com 通信联系人: 章明, 男, 工程师. ORCID: 0000-0003-3529-4259. E-mail: zhgmg@163.com

10.3785/j.issn.1008-973X.2016.01.013

TP 273

A

1008-973X(2016)01-0085-08