高中数学常见三种解题思路的研究

常晓兵

（新疆大学附属中学 新疆乌鲁木齐830001）

高中数学常见三种解题思路的研究

常晓兵

（新疆大学附属中学 新疆乌鲁木齐830001）

高中数学题目繁多，很多学生都深陷题海，难以自拔。这就是在平时的训练中，只注重解题，而忽视了总结。造成学数学越学越累，感觉有做不完的题，直至筋疲力尽逐渐对数学失去兴趣。很多题目都是有共同的解题思路，这需要我们做完题后“回头看看”，把这些有共同特征的题目放在一起，就会看出他们的共同之处。

在浩瀚的题海中通过笔者的总结、归纳，以下三种方法在高中数学题目解题过程中出现的频率非常高，现将这三种方法的解题思路、过程及常见题型总结精炼出来，方便广大学子乘风破浪，在题海中扬帆远航。

一、待定系数法的应用策略

对于某些数学问题，如果得知所求结果具有某种确定的形式，则可引进一些尚待确定的系数（或参数）来表示这种结果，然后利用已知条件通过变形与比较，根据恒等关系列出含有待定系数的方程（组），解之即得待定的系数，进而使问题获解，这种常用的数学基本方法称之为“待定系数法”。待定系数法的实质是方程思想，这个方法是将待定的未知数与已知数统一在方程关系中，从而通过解方程（组）求得未知数。

运用待定系数法求解问题，其基本步骤是：第一步，确定所求问题含有待定系数的解析式；第二步，根据恒等的条件，列出一组含待定系数的方程；第三步，解方程组或者消去待定系数，从而使问题得到解决。

题型一：用待定系数法求函数的解析式

例1：已知函数f（x）＝x2，g（x）为一次函数，且一次项系数大于零，若f（g（x））＝4x2－20x＋25，求g（x）的表达式。

破题切入点：一次函数的解析式具有固定的形式y＝kx＋b，求函数的解析式就是求出参数k，b，根据f（g（x））＝4x2－20x＋25，比较函数两边的系数即可解决问题。

题型二：用待定系数法解几何问题

例2：若焦点在x轴上的双曲线的一个焦点到一条渐近线的距离等于焦距的，则该双曲线的渐近线方程是（ ）

答案：C

则它的一个焦点到一条渐近线的距离为d，

所以渐近线与x轴的夹角为30°，

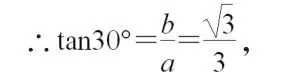
总结提高：待定系数法解题的关键是依据已知，正确列出等式或方程.要判断一个问题是否适用待定系数法求解，关键是看所求解的数学问题是否具有某种确定的数学表达式，如果有，就可以用待定系数法求解.例如数列求和、求函数式、求复数、解析几何中求曲线方程等，这些问题都具有确定的数学表达形式，所以都可以用待定系数法求解.

二、分析法与综合法应用策略

综合法：利用已知条件和某些数学定义、公理、定理等，经过一系列的推理论证，最后推导出所要证明结论成立，这种证明方法叫做综合法。

分析法：从要证明的结论出发，逐步寻求使它成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止，这种正面的方法叫做分析法。

综合法往往以分析法为基础，是分析法的逆过程.但更要注意从有关不等式的定理、结论或题设条件出发，根据不等式的性质推导证明.分析法是逆向思维，当已知条件与结论之间的联系不够明显、直接，或证明过程中所需要用的知识不太明确、具体时，往往采用分析法，特别是含有根号、绝对值的等式或不等式，从正面不宜推导时，常考虑用分析法.注意用分析法证题时，一定要严格按格式书写。

题型一：综合法在三角函数中的应用

题型二：综合法在立体几何中的应用

例4如图，如图，在三棱锥P－ABC中，D，E，F分别为棱PC，AC，AB的中点.已知PA⊥AC，PA＝6，BC＝8，DF＝5.

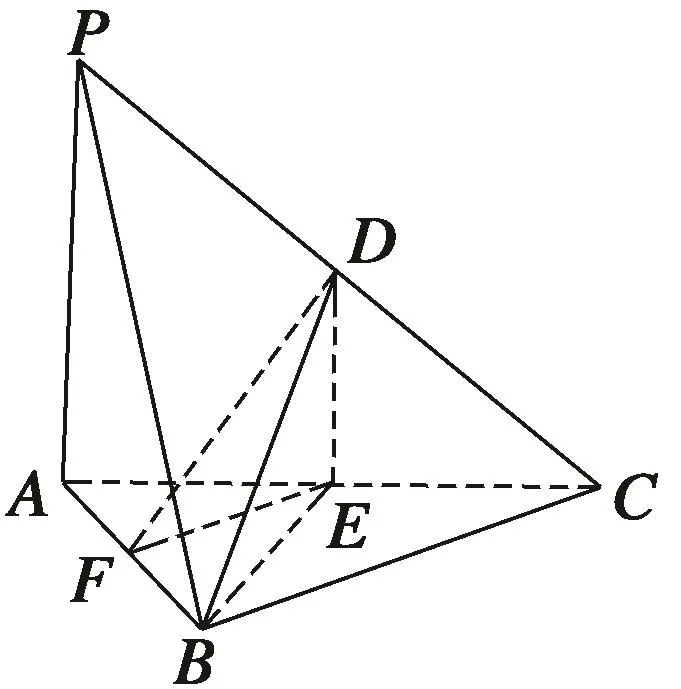
求证：（1）直线PA∥平面DEF；

（2）平面BDE⊥平面ABC.

证明：

（1）因为D，E分别为棱PC，AC的中点，

所以DE∥PA.

又因为PA⊄平面DEF，DE⊂平面DEF，

所以直线PA∥平面DEF.

（2）因为D，E，F分别为棱PC，AC，AB的中点，PA＝6，BC

又 因 为DF＝5，故DF2＝DE2＋EF2，所 以 ∠DEF＝90°，即DE⊥EF，又PA⊥AC，DE∥PA，所以DE⊥AC，因为AC∩EF＝E，AC⊂平面ABC，EF⊂平面ABC，所以DE⊥平面ABC，又DE⊂平面BDE，所以平面BDE⊥平面ABC。

综合法和分析法是直接证明中两种最基本的方法，也是解决数学问题时常用的思维方式.综合法的特点是由原因推出结果，分析法的特点是由结果追溯到产生这一结果的原因.在解决问题时，经常把综合法和分析法结合起来使用：根据条件的结构特点去转化结论，得到中间结论，根据结论的特点去转化条件，得到另一中间结论，根据中间结论的转化证明结论成立.

三、整体处理问题的策略

整体思想就是在研究和解决数学问题时，通过研究问题的整体形式、整体结构、整体特征，从而对问题进行整体处理的解题方法.从整体上去认识问题、思考问题，常常能化繁为简，同时又能培养学生思维的灵活性.所谓整体化策略，就是当我们面临的是一道按常规思路进行、局部处理难以奏效或计算冗繁的题目时，要适时调整视角，把问题作为一个有机整体，从整体入手，对整体结构进行全面、深刻的分析和改造，以便从整体特性的研究中，找到解决问题的途径和办法.

题型一：整体处理问题的策略在函数中的应用

例5：若函数y＝f（x）的定义域为[－1，1），则f（2x－1）的定义域为________.

破题切入点 本题是抽象函数的定义域问题，这类问题的解决要有整体意识，把2x－1作为一个整体，其取值范围与y＝f（x）中的x取值范围相同.解决这类问题要注意两个问题，①等范围代换，即将括号内的式子作为一个整体考虑，取值范围相同；②求定义域问题就是求自变量的取值范围.

答案：[0，1）

解析：由y＝f（x）的定义域为[－1，1），则－1≤2x－1＜1，

解得0≤x＜1.

所以f（2x－1）的定义域为[0，1）.

题型二：整体处理问题的策略在三角函数中的应用

破题切入点：

与已知条件2sinθ－cosθ＝1联立，即可用t的代数式表示sinθ、cosθ，再根据sin2θ＋cos2θ＝1求得t的值.

解得t＝0或t＝2.

所以所求的值为0或2.

用整体思想解题过程简洁明快，而且富有创造性，有了整体思维的意识，在思考问题时才能使复杂问题简单化，优化解题过程，提高解题的速度.强化整体意识，灵活选择恰当的整体思想方法，可以大大提高学习效率.