基于最小二乘法的反应釜参数整定系统设计
2016-12-10关宏伟李园梁立达马修水
关宏伟,李园,梁立达,马修水
(1.宁波大红鹰学院机械与电气工程学院,浙江宁波315175;2.浙江大学宁波理工学院,浙江宁波315100)
基于最小二乘法的反应釜参数整定系统设计
关宏伟1,李园2,梁立达2,马修水2
(1.宁波大红鹰学院机械与电气工程学院,浙江宁波315175;2.浙江大学宁波理工学院,浙江宁波315100)
反应釜具有工艺复杂,干扰量多且难以测量等特点,获得其模型较为困难。本文以反应釜为对象,运用最小二乘法对其进行辨识,获得模型参数。根据系统模型对其进行参数整定,系统的性能指标为超调量2%,峰值时间10min,上升时间6.5min,调整时间5min,衰减比为5。
反应釜;最小二乘法;动态性能
一、引言
在工业生产过程中,反应釜具有非线性、时滞性、时变性。为了取得良好的反应釜温度控制效果,张文丽和逢海萍将模糊控制算法与PID控制算法相结合,设计了一种自调整模糊PID控制器,该控制器具有使系统超调量小、调整时间短、鲁棒性好且算法简单等优点,是一种提高聚合反应釜温度控制效果的有效方法[1]。Barry和Sandro采用GMC方法控制反应釜温度,进一步考察了操作条件与过程参数变动时被控过程的鲁棒性,得出了GMC的鲁棒性明
显强于双模控制的结论[2]。周晓燕给出了冷剂流量对反应釜内温度的传递函数,设计了按偏差分档控制的智能控制系统。在控制方法上,采用了基于规则修改的自适应模糊控制和不完全微分PID控制算法相结合的方法[3]。综上所述,他们所设计的只针对个别反应的反应釜,不能面向多种类型的反应釜,因而存在着程序复杂、单一性等缺点。
本文利用计算机技术,获得反应釜的温度实时数据(采样),从这些数据中提取反应釜的模型特性,根据最小二乘法原理进行系统识别,获得τ、T、K等描述对象特性的参数,然后进行PID参数整定(比例系数P,积分时间Ti,微分时间Td)获得良好的温度控制效果。
二、系统结构及温度控制原理框图
反应釜是物理或化学反应的容器,实现工艺要求的加热、蒸发、冷却及低高速的混配功能。反应釜基本结构如图1所示,主要由加热系统、冷却系统、进出料三大系统组成,详见表1,包含的主要元器件详见表2。

图1 反应釜的基本结构

表1 反应釜系统组成

表2 反应釜元器件组成

图2 反应釜釜温控制框图
将单回路盘管冷却反应釜和执行器看做一个整体,称为广义被控对象,釜温控制框图如图2所示。
三、建模方法
PID参数整定分为两类。一是工程整定法,主要依赖于工程经验,直接在控制系统中进行调试。二是理论计算整定法,依据系统数学模型,经过理论计算确定控制器参数。理论计算法有机理建模法、作图法和最小二乘法等。
机理建模法以冷却剂流量对反应釜内温度的影响为例。通过机理获得系统模型,必须要知道反应物的浓度、盘管冷却液的流量和反应釜的传热面积等相关参数。很显然这些数据在测量中存在一定困难。这只是一个变量对反应釜温度变化的影响,还有其他的影响因素,比如加热棒的功率、进水的温度,冷却水的温度,反应釜的体积和形状等。因此:在工程中,通过机理法实现对被控对象的的数学建模可行性不大。
作图法开启实验操作,将系统置于开环,获得系统的阶跃响应曲线图,自衡对象曲线图近似S型。根据阶跃响应作图法[4]得τ=0.5,T=15,K=35。现知道被控对象的数学模型特性,故根据Ziegler-Nichols法[5]获得PID控制器的相关参数为P=14.8;Ti=1;Td= 0.25。
整定结果:温度一直处于振荡过程,振荡周期为
10min,振幅1.4℃。
分析原因如下:(1)阶跃响应曲线的拐点不易找准,切线的方向也具有一定的随意性。(2)做切线时,与横纵坐标交点读数需要估计,存在着一定的误差。(3)根据经验公式获得的PID参数需要重新调整,需要一定的经验。综上所述:作图法耗时较多,且对工程技术人员的素质要求较高。
最小二乘法由于反应釜内安装了热电偶,反应釜内的温度可以时刻在计算机上显示和记录,这些温度是反应釜在时间序列上的工作点,可以体现反应釜模型特性。将这些工作点画在坐标图上,近似一条S型曲线,而反应釜为自衡对象,其模型形式为,(其中K、T因不同反应对象而不同)故只要求出K、T、τ就可以进行参数整定。其一阶阶跃输出为,为此只要运用最小二乘法,拟合反应釜时间序列上的工作点就可以得到被控对象的模型。
应用中,选择冷却水阀开度为65%。待反应釜达到稳态时(70℃),施加阶跃扰动,记录实时数据,以时间为自变量,反应釜的温度为因变量,记录结果到附表1中(见P25页)。拟合曲线后可以得到模型对象的三个参数:K=36.7530,T=10.4611,τ=0.0281。求取最小均方差,得到最小均方差是36.4551。

表3 反应釜动态性能一览表
由于τ比较小,采用PI控制器,根据Ziegler-Nichols法,得到控制器相关参数为P=0.11,Ti=0.3。将PI串联到控制回路中,使之构成闭合回路,获得该系统的动态性能示于表3。
作图法的整定结果导致系统一直处于振荡状态,此状态虽处于稳定,但是始终达不到设定要求,此时反应釜的各个元器件的状态不断切换,长此以往将缩短系统的使用寿命。而利用最小二乘法的整定响应曲线在3个波峰之后基本趋于设定温度。综上所述:利用最小二乘法的控制效果明显优于作图法。
四、结果与讨论
反应釜的温度控制过程中需要工人即时监管和丰富经验,不能完全摆脱人工干预而完全实现自适应控制。此外,对于当前小批量生产的反应釜反应过程,每次生产工况都会有所不同,其具体反应机理都会产生变化。
运用最小二乘法进行建模,当设定不同参数时,该函数可代表不同受控对象。最小二乘法建模法的最大特点就是不针对个别反应,可面向多种类型的反应釜,即无论参数如何变化(即受控对象不断变化),均可通过此方法准确地进行温度控制操作并实现控制目标。
[1]张文丽,逢海萍.聚合反应釜自调整模糊PID控制器的设计及仿真[J].青岛科技大学学报(自然科学版),2005(2):132-135.
[2]M.Santos,A.l.Dexter.Control of Cryogenic Process Using Fuzzy PID Scheduler[J].Control Engineering Practice,2002,10: 1145-1152.
[3]周晓燕.反应釜智能控制器研究与开发[D].南京理工大学硕士学位论文,2005:1-73
[4]金以慧,方崇智.过程控制[M].北京:清华大学出版社,2001.
[5]Cheng Ching Yu.Autoturing of PID controllers:Relay Feedback Approach[M].Springer,1999.
(责任编辑:袁媛)
Design of the Parameter Adjusting System of Reaction Kettle Based on the Least Square Method
GUAN Hong-wei1,LI Yuan2,LIANG Li-da2,MA Xiu-shui2
(1.School of Mechanical and Electronic Engineering,Ningbo Dahongying University,Ningbo 315175,China; 2.Ningbo Institute of Technology,Zhejiang University,Ningbo 315100,China)
The reaction kettle has the characteristics of complicated process,much disturbance and measurement difficulty,so it is difficult to obtain its model.The least square method is used to identify and obtain the model parameters of the reaction kettle.According to the system model,the parameters of the system are adjusted,i.e.the system performance is over 2%;the peak time is 10min;the rise time is 6.5min;the adjusting time is 5min; and the attenuation ratio is 5.
reaction kettle;least square method;dynamic performance
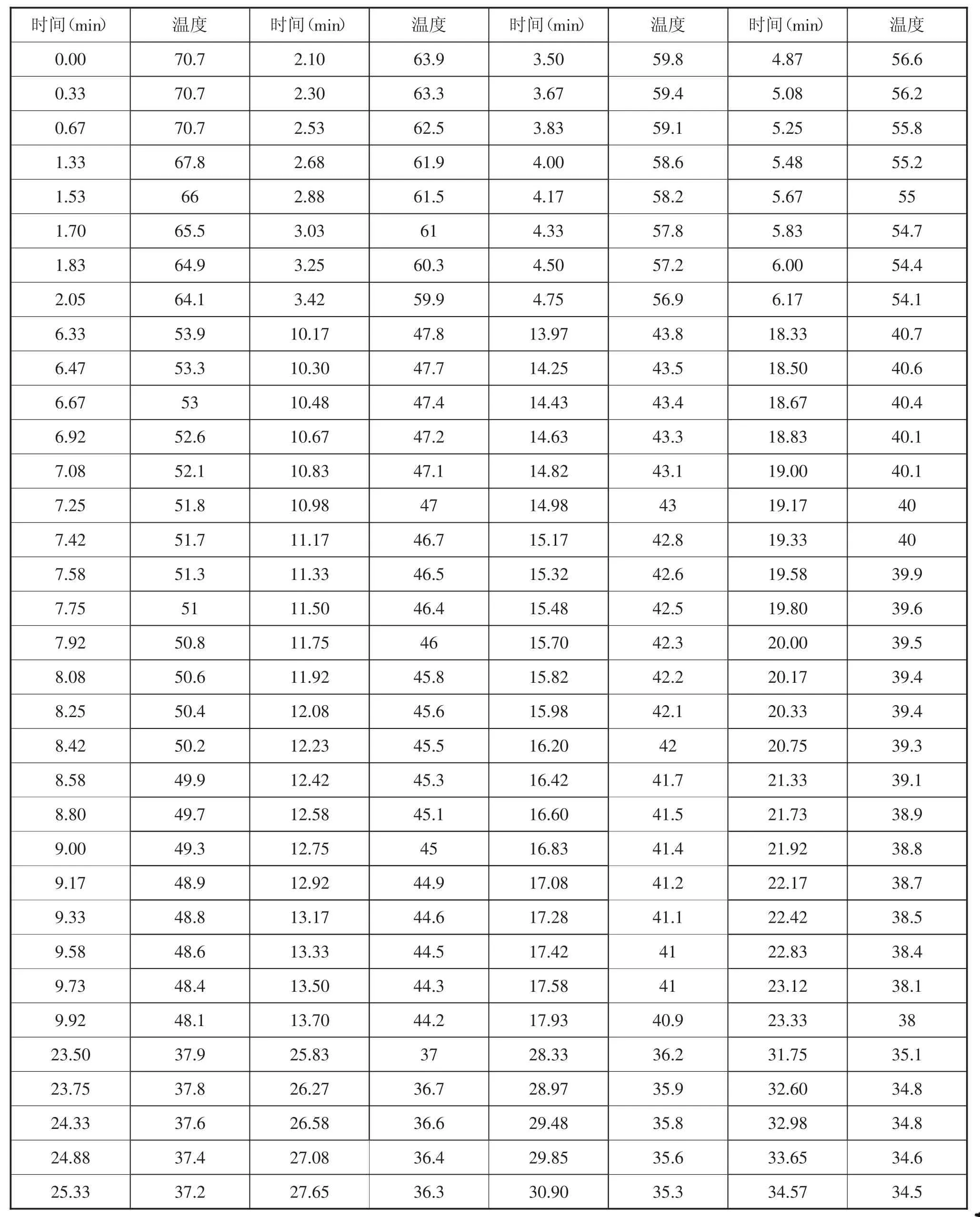
附表1 阀门开度65%反应釜实时温度
TG155
A
2016-08-15
关宏伟(1977—),男,吉林人,博士,讲师,研究方向:复杂系统建模。E-mail:ghw_nit@126.com.
浙江省教育厅科研项目(Y201432757),国家自然科学基金项目(61304081),浙江省自然科学基金资助项目(LQ13F030007);宁波市
创新团队资助项目(2012B82002,2013B82005)
1671-802X(2016)05-0022-04
