一种自适应变异子空间搜索演化算法研究

林广明，唐飞，卢鑫，陈三风

（1.深圳信息职业技术学院科研处，广东 深圳 518172; 2.深圳信息职业技术学院信息技术研究所，广东 深圳 518172）

一种自适应变异子空间搜索演化算法研究

林广明1，唐飞1，卢鑫2，陈三风2

（1.深圳信息职业技术学院科研处，广东 深圳 518172; 2.深圳信息职业技术学院信息技术研究所，广东 深圳 518172）

本文提出一种新的自适应变异子空间搜索演化算法，新算法包含如下性能：1）自适应选择变异算子，在变量子空间平衡局部搜索和全局搜索；2）通过多父体杂交交换全局搜索信息；3）用最好的个体替换最差个体的选择策略，降低选择压力确保找到全局最优解。这些优势增强了算法求解函数优化的鲁棒性和广泛性,并证明了算法的收敛性。

自适应变异；多父体杂交；子空间搜索

引言

随着日益将演化算法应用到实际问题中，人们越来越关注用遗传算法来求解实数优化问题[1,2,3,4,5]。近期研究[6,7,8,9]表明求解实数优化问题时用杂交算子得到较好的结果。因此目前对实数函数优化问题的研究中，人们主要集中于研究如何找到一个有效的杂交算子，而它们都有各自的优缺点。本文首先对这些算子进行分析，然后详细描述作者提出的自适应子空间重组算子，然后从理论和数据试验证明自适应子空间搜索算法SMSSEA（Selfadaptive Mutation and Subspace Searching Evolutionary Algorithm）不仅能求解带不等式约束的非线性的且有复杂场景的函数优化问题，而且本算法 也具有搜索的遍历性与收敛的单调性等特点。

1　常见的变异算子

在实数编码中，变异算子的重要性尚存在一定的争论，但是我们认为变异算子的产生种群多样性，或者说加强空间的探索能力的特征是必须保留的，这才是这个算子的精髓。

1.1均匀变异算子

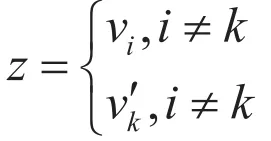
1.2正态变异算子

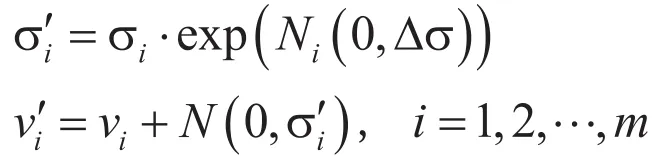
1.3非一致性变异算子

非一致性变异算子描述如下：

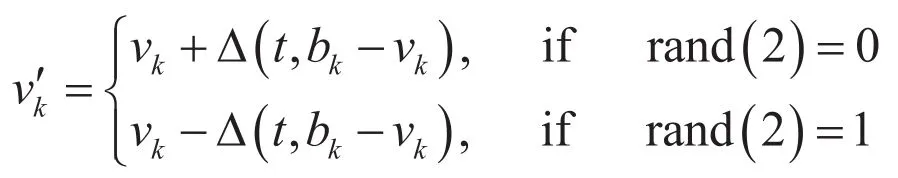
这里如果rand(2)表示将正整数模2所得的均匀产生的随机数，t为当前的演化代数控制变量，函数的值域是[0，y]，从表达式得出：并使得当不断t增大时，接近于0的概率也增加。也就是t的值越大，取值接近于0的值的可能性就越大，使得算法在演化初期能够搜索的范围较大，而在搜索的后期主要是进行局部搜索了。

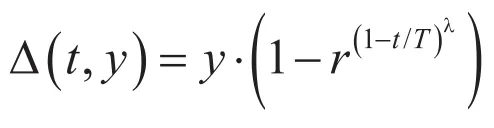
其中，r是[0，1]上的一个均匀随机数，T表示最大的代数，是决定非一致性程度的参数，起调整局部搜索区域的作用，其取值范围一般在2到5之间。

1.4自适应变异算子

自适应变异算子是更为合理的使得对于适应值大的个体在较小范围内搜索，而对于使适应值小的个体在较大范围内搜索。该算子类似于模拟退火中温度，引入了解的变异温度的概念。

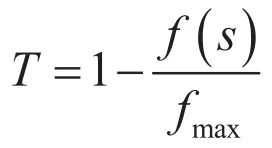
自适应变异算子的变异方式与前面介绍的非一致变异基本相同，只是将其中的演化代数t为T，函数的具体表达式改变为：

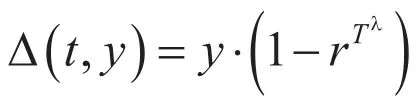
2　自适应子空间搜索算子

郭淘[14]多父体杂交算子引入了子空间的概念，并且将父体组合的空间从传统意义上的[0，1]范围扩展为[-0.5，1.5]，因此大大扩展了搜索的范围，由此也得到更为良好的结果。郭淘多父体杂交算子可以这样来描述：

设计一个多父体杂交算子时，有两点需要考虑：一是由于多父体导致的整个群体的割裂，。

由于GT多父体算子已经有多个实验证明它在收敛性方面的优良特性，因此，我们将以它作为基准，进行改进，以期得到更为优良的杂交算子。

引入子空间的概念，记D中M个点Xj，j＝1,2,…,M所张成的子空间为：，其中满足条件。然后从V中随机选取s个点，最后得到的后代个体为：。条件可保证当基函数时，它们组成的子空间VM能覆盖定义域S（包括S的边界）。这样一来，既可保证搜索的遍历性，也可保证子群体的多样性。

3　自适应子空间搜索算法SMSSEA

对于一个非线性规划问题，可以一般性地可表示如下：

习近平精准扶贫思想在中国取得了巨大成就，得到了国际社会的深度赞誉，是对世界扶贫理论的贡献，充分体现和发挥了中国的社会主义制度的优势；习近平精准扶贫思想是以习近平同志为核心的党中央治疆方略的重要内容，是对共产党治疆理论的创新与发展。南疆的特殊区情决定了南疆精准扶贫的复杂性和艰巨性。南疆精准扶贫虽然取得了显著的成效，但由于历史的欠帐太多，南疆精准扶贫的道路仍然漫长而艰巨。

满足条件:

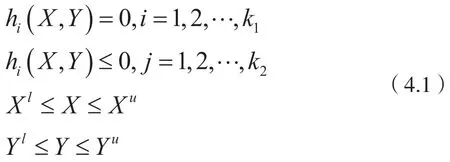
其中X是一个p维的实型向量，Y是一个q维的整型向量，且X在到间取值，Y在到间取值，目标函数、等式约束和不等式约束一般都是非线性函数，并且都包含了实型和整型变量。

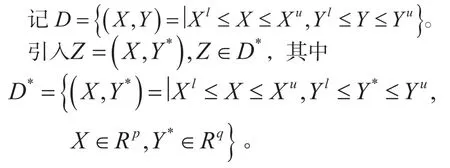
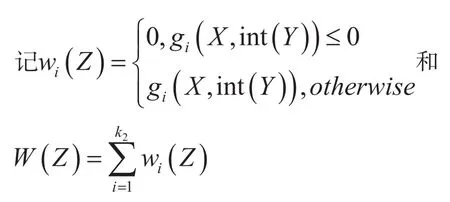
定义布尔型函数better：

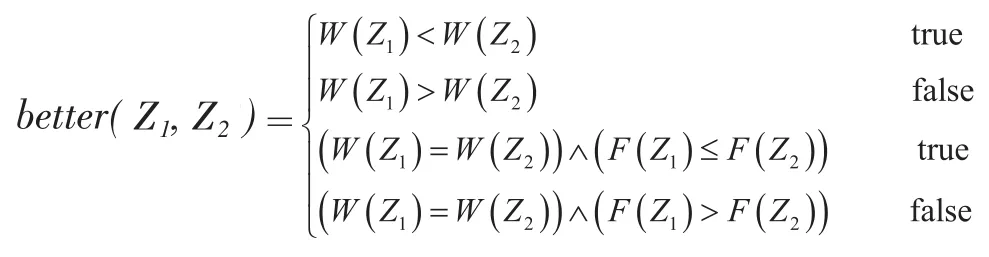
表达式（4.1）中既包含了不等式约束，又包含了等式约束。在处理约束时，我们采用的方法是惩罚函数，一个常用的函数形式是：

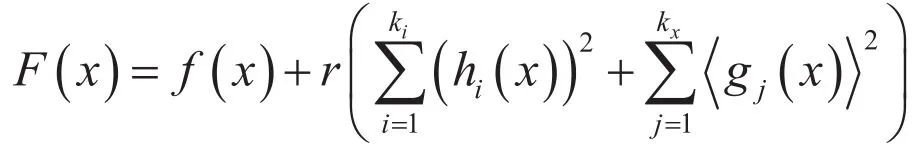
其中＜gj(x)＞表示max {0,gj(x)}，r为惩罚因子。

由于算法已将不等式约束条件计入better函数中，因此实际上采用的适应函数中只含有等式约束的惩罚项，即：

由此定义以下适应函数：

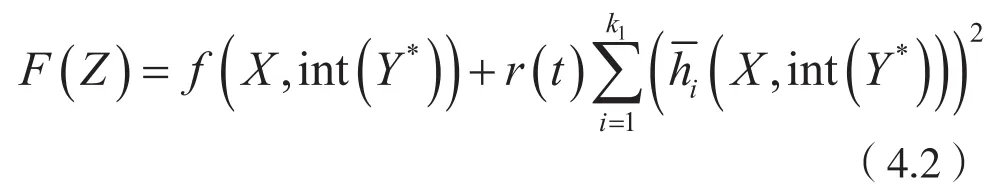
另外记D中M个点(Xj,Yj)，j＝1,2,…,M所张成的子空间为：

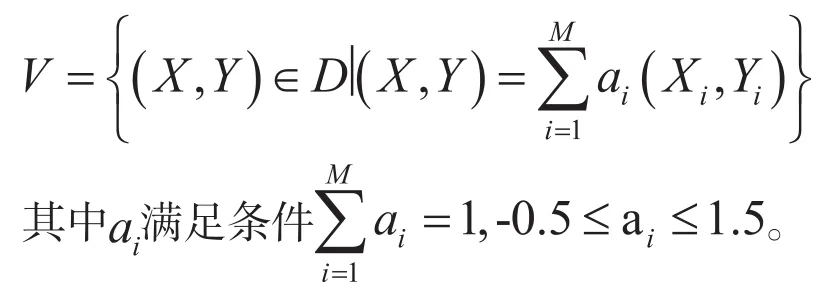
综上所述，自适应子空间搜索算法SMSSEA可描述如下：

Begin

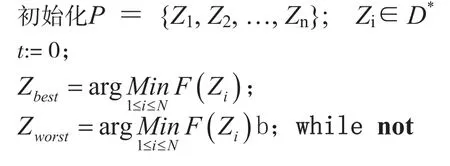
其中N为群体向量P的大小,（M-1）为子空间V的维数，t为迭代的次数。ε为解的精度。表示把 Xi(i=1,2,…,N) 中使f(X)最小的那个变量（个体）记作Xbest。

注1：采用SMSSEA算法中所描述的惩罚函数，它能对整个评估函数的值起决定性作用而影响问题的求解精度。因此，参照文献[15]，我们引入规范化方法。所谓规范化方法就是找到约束条件中系数绝对值最大的一个，然后用它的倒数去乘该约束条件。如[14]中例2.1的第三个约束条件：

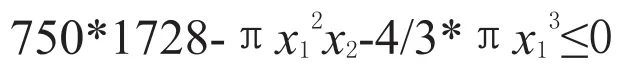
它的最大系数为750*1728=1296000，该约束条件除以1296000以后，变成

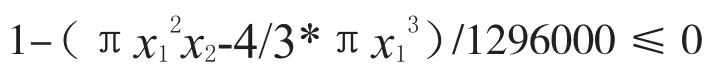
这时它对整个评估函数的影响就缩小了一百万倍。经过规范化处理后的等式约束条件记作，这时

有时我们也用约束函数的“绝对值”代替“平方”，以减少计算量：

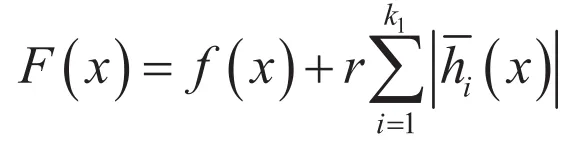
采用该方法进行的数值实验得到比较理想的结果。

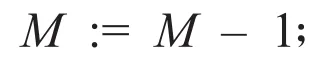
其中η是一个与计算精度要求有关的变量，且η＞ε。例如，如果计算精确要求是ε= 10-14，那么我们就可将η设为10-2或10-3。

注3：一般来说惩罚因子r都是设置为不变，但也有人将其设为可变的，如Cello Cello[16]应用自适应惩罚法，但其控制过程太过复杂（用两个群体）。我们也将其设置为可变化的（可调整的），即r = r(t),t为迭代参数，它根据计算过程的反馈信息进行调整，故又称r(t)为自适应惩罚因子。

注4：郭涛算法中只有重组算子而无变异算子，若对问题的性质有更多的信息可以利用的话也可以引入变异操作。如在[14]中例2.3中，由于最小值与个体的排列顺序有关，在算法中引入变异——对个体的分量按降序进行排列，这样得出的结果优于未排序时得出的结果。

注5：停机条件可根据用户要求选择下述条件之一：

（1）连续k代Zbest的数值不变；

（2）better（Zworst ,Zbest）=True；

（3）当t≥TMax时，TMax为一充分大的正整数，即设定的最大演化代数；

注6：最近吴志健等在文献中[17]提出了一种“精英子空间搜索策略”：即在选择子空间VM中的M个基点时，取，其余的（m-1）个基点，则从P（t）中随机地选取。这样可以加速算法的收敛性，但它有可能导致收敛到局部最优解。我们把这个策略也可用到SMSSEA算法中。即用：

来代替算法中的：

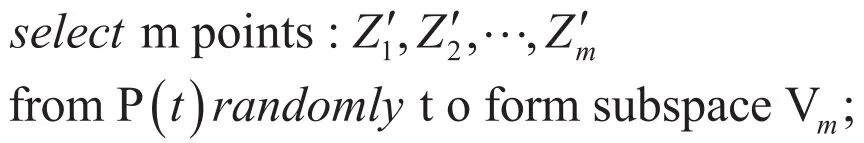
这时，我们称其为带精英自适应子空间搜索算法。

4　SMSSEA算法的收敛性分析

算法SSSEA可简记为一阶（齐次 Markov链）随机差分方程组：

其中p(0)为初始群体；算子selection是以算子better函数为标准每次仅淘汰群体中的一个最差个体；算子recombination是采用（多父体杂交）子空间搜索法，算子mutation只有在子空间搜索失利时才进行，而且只对群体中的最差个体进行变异运算：Z=Zworst+N（0,σ）I，其中I=（1,1,…,1），N（0,σ）是均值为0，方差为σ的正态分布随机变量,也就是说:向量N（0,σ）I的每个分量都是随机产生的。

由于SMSSEA算法中的选择运算S（selection算子）、变异运算M(mutation)与重组运算R（recombination算子）都与时间（代数t）无关。由（4.3）式可得：

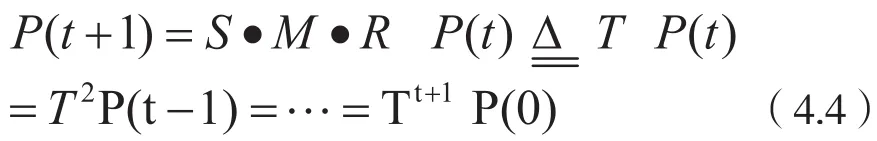
其中T＝S·M·R为随机转移算子，它是由重组算子R、变异算子M与选择算子S复合而成。

转移算子S·M·R实现的是将P(t)中的某一个体Zi（Zworst）转移到P(t＋1)的某一个体Zj，其余的个体不变化，Zj可以是VM中随机产生的S个个体中挑选出来的最佳个体，也可能是由Zi经过变异而产生的。由于VM是由P(t)中随机选取的M个点的非凸组合张成，故VM可以复盖P(t)中N个基点（线性无关）的凸组合张成的空间，如果M＞N，且P(t)中的个体均匀分布在D中的话。

引理1[18]具有不可分转移矩阵T的有限齐次马尔科夫链{P(t),t 0}以概率1无限次地访问Dε的每一状态（网格点）。

为了证明（4.4）的收敛性，我们将要应用上述引理，因此，首先要证明T是不可分的。如所周知：若存在正整数t，使得Tt ={ pij(t)}的元素pij(t)＞0，则T是不可分的。在证明下述定理时将要证明这一点。

定理1（算法SMSSEA的收敛性） 若算法SMSSEA的初始群体P（0）在Dε中均匀分布，则该算法依概率1收敛于问题（2.2）的全局最优解X*，即

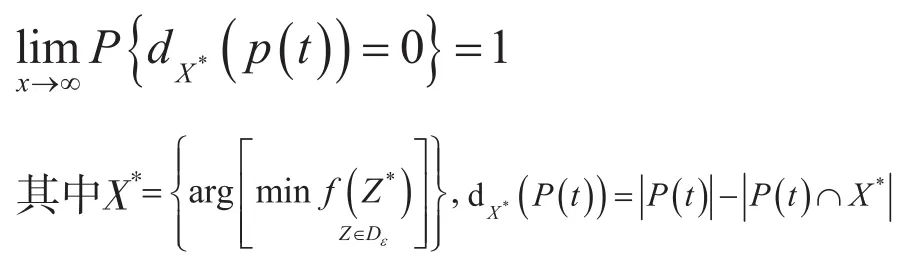
证明：首先证明T={pij},i,j∈Dε是不可分的。这就要证明存在正数t，对Dε中的任何解x*∈X*，从初始群体出发在t步内到达x*的概率P＞0。

不失一般性，对于2维问题，可设n=2，ε=1/2k。

Dε={Z∈D|Z=（iε,jε）,i,j 为整数}。

记P（0）={Z1，Z2，…，ZN}，Zi∈Dε，其中N＞n=2

设m=3，若随机选取的三个点为Zi、Zj与Zk。若它们线性无关，则形成的二维子空间，

它点a1Zi+a2Zj+a3Zk组成，由于a1+a2+a3=1且，故有。这就是说，如果解,那么从初始群体出发，下一代找到落在子空间V3中的解x*的ε邻域的概率，其中，s为在子空间V3中搜索的点的个数。即,如果x*落在三角形ΔABC上，那么经过有限代t1到达x* 的ε邻域的概率大于0。如果x*不落在ΔABC上，由于P(0)中的个体均匀分布于Dε中，而且N ＞＞n，故P(0)必存在不属于ΔABC中的个体，那么它可与P(0)中另外随机选取的两个个体形成新的子空间（三角形）。

下面证明：

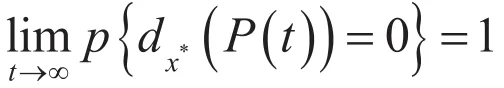
从上面的证明可知，从初始群体中的某一点出发，经过有限代t1到达的概率为1。由于SMSSEA算法每一代只淘汰群体中的最差个体，当t＞t1时，必有，即，以后永远保留在群体中，从P(t1)起，经过t2代，到达的概率为1。这时有两种可能：，或。不管是那种情况，根据SMSSEA的淘汰策略，在t≥t1+t2时，将有，如此下去，经过代后，P(t*)的全部个体的概率为1。这时，满足停机条件：better(Zworst,Zbest)=T。也就是说，

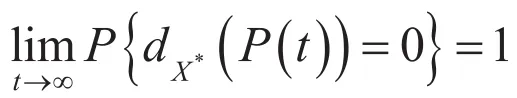
定理得证。

5　数值实验

用SMSSEA求解Shekel问题

Shekel's函数族:

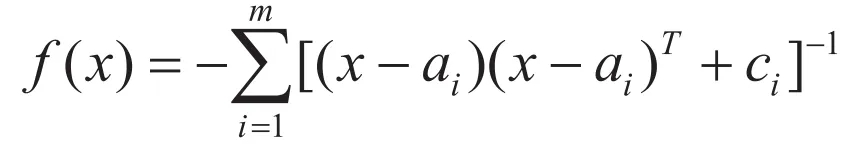
表6.1　Shekel函数，和[21]

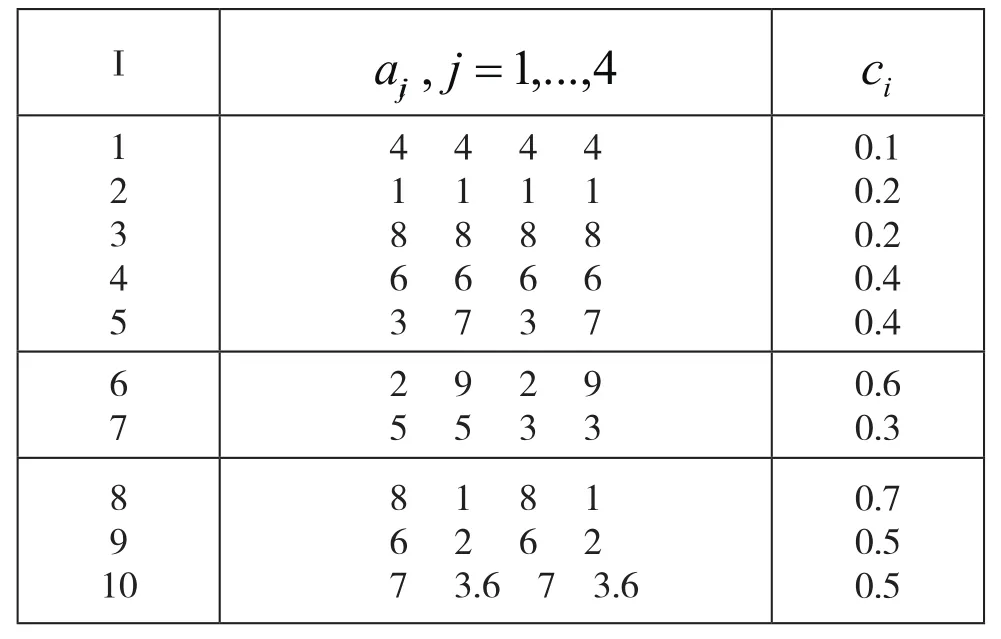
表6.1　Shekel函数，和[21]

I aij,j=1,...,4 ci1 2 3 4 5 4　4　4　4 1　1　1　1 8　8　8　8 6　6　6　6 3　7　3　7 0.1 0.2 0.2 0.4 0.4 6 7 2　9　2　9 5　5　3　3 0.6 0.3 8 9 1 0 8　1　8　1 6　2　6　2 7　3.6　7　3.6 0.7 0.5 0.5

在这节中，我们来比较CEP,FEP,IFEP 和SMSSEA来求解3个Shekel问题。测试函数的维数是n=2，代数为100。CEP,FEP,IFEP 和 SMSSEA的比较结果由表6.2给出，这里我们每个函数进行50次试验，种群大小为N=100，子空间的大小为M=8，我们从表6.2可以看到SMSSEA克服了EP家族在求解Shekel的困难.关键是通过多父体杂交交换全局搜索信息，避免了陷入局部最优不能自拔。

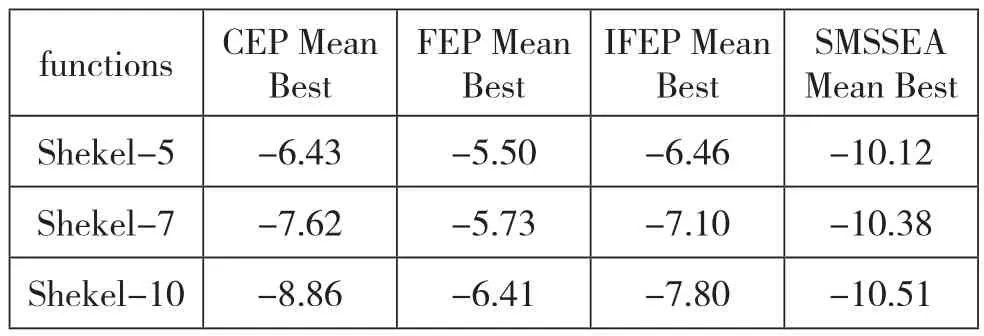
表6.2　CEP,FEP,IFEP [21]和 SMSSEA 在求解Shekel函数族的比较

其中“Mean Best”表示50次运算在最后一代发现函数最好值的平均。

6　小结

本文提出了一个新的以多父体杂交为主的演化算法——自适应子空间搜索算法SMSSEA。在研究已有的求解单峰单目标函数优化问题的演化算法的基础上，对该算法进行了收敛性分析，并通过数值试验验证了算法的有效性和可靠性。SMSSEA可以用来求解各种类型的复杂函数优化问题，无论是包括带约束（不等式约束与等式约束）条件，还是不带约束条件的函数优化问题、以及0-1型变量、整型变量、混合整数型变量的非线性规划问题。对不同的类型的优化问题只要输入求解问题的适应函数和约束条件的表达式以及变量的上、下界限即可，不需要修改算法步骤，且在一般情况下，可较快地找到优化问题的全局最优解。

[1]Z.Michalewicz and N.Attia:Evolutionary optimization of constrained problems,in Proceedings of 3rd Annu.Conf.Evolutionary Programming:World Scientific,1994,98～108

[2]Z.Michalewicz:Evolutionary operators for continuous convex parameters spaces,In Proceedings of 3rd Annu.Conf.Evolutionary Programming:World Scientific,1994,84～97

[3]Z.Michalewicz:Genetic algorithms,numerical optimization,and constrains,in Proceedings of 6th Annu.Conf.Evolutionary Programming,1995,151～158

[4]Z.Michalewicz:Handling constraints in genetic algorithms,in Proceedings of 4th Int.Conf.On Genetic Algorithms.1991,151～157

[5]D.Powell and M.M.Skolnick:Using genetic algorithms in engineering design optimization with nonlinear constraints,in Proceedings of 5th Int.Conf.On Genetic Algorithms.1993,424～430

[6]N.Srinivas and K.Deb:Multiobjective optimization using nondominated sorting in genetic algorithms.Dept.Mech.Eng.,Indian Inst of Technol.Kanput,India,Tech.Rep.,1993

[7]J.Paredis:Co-evolutionary constraint satisfaction,in Proceedings of 3rd Conf.Parallel Problem Solving from Nature.World Scientific,1994,46～55

[8]R.G.Reynolds:An introduction to cultural algorithms,in Proceedings of 3rd Annu.Conf.Evolutionary Programming:World Scientific,1994,131～139

[9]Z.Michalewicz and G.Nazhiyath:Genocop III:A coevolutionary algorithms for numerical optimization problems with nonlinear constraints,in Proceedings of IEEE Int.Conf.On Evolutionary Programming:IEEE Press,1995,647～651

[10]Goldberg,D.E.,Real-Coded Genetic Algorithms,Virtual Alphabets,and Blocking.Complex Systems 5(2),139-168,1991

[11]Deb,K.and Agrawal,R.B.,Simulated Binary Crossover for Continuous Search Space.Complex Systems 9(2),115-148,1995

[12]Ono,I.,and Kobayashi,S.,A Real-Coded Genetic Algorithm for Function Optimization Using Unimodal Normal Distribution Crossover.In Proceedings of the Seventh International Conference on Genetic Algorithms,246-253,1997

[13]Tsutsui,S.,Yamamura,M.,and higuchi,T.,Multi-Parent Recombination with Simplex Crossover in Real-Coded Genetic Algorithms,In Proceedings of the Genetic and Evolutionary Computation Conference(GECCO-1999),657-664.

[14]Guo Tao,Kang Lishan.A new evolutionary algorithm for function optimization.Wuhan University Journal of Nature Science.Vol.4 No.4 1999,409～414

[15]Kalyanmoy Deb.GeneAS:A robust optimal design technique for mechanical component design.Evolutionary algorithm in engineering application:Springer-Verlag,1997,497～514

[16]Carlos A.Cello Cello:Self-adaptive penalties for GA-based optimization,in Proceedings of the Congress on Evolutionary Computation,Washington,D.C USA,IEEE Press,1999,537～58

[17]吴志健，康立山，邹秀芬.一种解函数优化问题的精英子空间演化算法，计算机应用，No.2,13-15,2003.[18]Rudolph,G.,Convergence of Evolutionary Algorithm in General Search Spaces,In Proceedings of the Third IEEE Conference on Evolutionary Computation,50-54,1996.

[19]Sandgren,E:Nonlinear integer and discrete programming in mechanical design,ASME J.Mechanical Design,1990,112:223～229

[20]J.F.Fu,R.G.Fenton and W.L.Cleghorn:A mixed integer-discrete-continuous programming method and its application to engineering design optimization.Engineering Optimization, 1991,17(3):263～280

[21]Yao Xin,Liu Yong,Lin Guangming.Evolutionary programming made faster.IEEE Trans.Evolutionary Computation,1999,3(2):82-102

【责任编辑：毛蔚】

A Study of Self-adaptive Mutation and Subspace Search Evolutionary Algorithm

LIN Guangming1,TANG Fei1,LU Xin2,CHEN Sanfeng2
（1.Department of Scientific Research,Shenzhen Institute of Information Technology,Guangdong Shenzhen 518172,China; 2.Institute of Information Technology,Shenzhen Institute of Information Technology,Guangdong Shenzhen 518172,China）

This paper presents a Self-adaptive Mutation and Subspace Search Evolutionary algorithm(SMSSEA).It is the combination of the multi- parent crossover and the elimination rule of the worst individual.The population size and the crossover size will lead the population's evolvement to diversity or convergence.When SMSSEA is applied in the optimization of multimodal function,it runs in different forms during the global and local optimization phrases.

Self-adaptive mutation; multi-parent crossover; Subspace search

TP301.6

A

1672-6332（2016）03-0030-07

2016-09-11

广东省自然科学基金资助项目（基金批准号：2015A030313587）深圳市科技计划（基金批准号：JCYJ20130401095559825，JCYJ20150417094158025）

林广明（1963-），男，博士，教授，研究方向：人工智能，演化计算。E-mail:lingm@sziit.com.cn