波生沿岸流的数值模拟研究*

汪 鸿，李训强*，朱首贤，张文静

(1.解放军理工大学 气象海洋学院，江苏 南京 211101；2.河海大学 海洋学院，江苏 南京 210098)



波生沿岸流的数值模拟研究*

汪 鸿1，李训强1*，朱首贤2，张文静1

(1.解放军理工大学 气象海洋学院，江苏 南京 211101；2.河海大学 海洋学院，江苏 南京 210098)

采用完全非线性Boussinesq方程建立的FUNWAVE模型进行波生沿岸流数值模拟研究，通过对不同斜坡地形和波浪入射条件下波生流的物理模型实验结果进行比较，验证了该数值模型能较准确地计算沿岸流；通过改变波浪的不同入射条件，对不同入射条件的沿岸流数值模拟得出：当其他条件不变时，仅入射波高增大时，沿岸流的流幅和幅值增大，幅值位置向深水移动；仅增大入射周期时，沿岸流的流幅显著增加，幅值的增加较小；斜坡地形坡度的改变能显著影响波生沿岸流的流幅和幅值，但对沿岸流幅值位置的水深影响不大。采用窄缝法处理动边界时，选择合适的窄缝起始水深对沿岸流的准确计算是十分必要的。

沿岸流；数值模拟；Boussinesq方程；窄缝法

波生沿岸流是由于近岸波浪的波高和波向分布不均匀产生的沿岸水流，它对近岸地形的塑造、物质输运和海岸线演变有重要影响，长期以来波生沿岸流的研究受到极大的关注[1-2]。由于波生流场的易变性，其现场观测比较困难[3-4]，因此，采用数值模型模拟研究波生流是较为有效的手段[5]。

近年来，国内外学者对波浪数值模型的研究和应用开展了很多工作，目前用于模拟近岸波生流的数值模型可分为两类：一类为波浪时均模型，一类为波浪时域模型。第一类模型将流体运动方程在波浪周期上进行平均，求解时均方程直接得到波生流场，而波浪则通过相应的波浪理论或模型，应用辐射应力概念进行考虑，这类模型比较多见[6-8]。第二类模型则直接针对波浪质点运动进行求解，将结果在多个波浪周期内平均得到波生流场。Boussinesq类波浪模型为第二类模型的典型代表[9]。这两种模型各有优缺点，前者计算速度快，但不能充分考虑波流相互作用，仅通过辐射应力不能充分考虑短波(波浪)的尺度效应，如波浪非线性以及波浪-波浪之间的非线性相互作用等；后者计算速度相对较慢，但实现了波浪运动同水流运动的完全耦合求解，更能准确地反映近岸区域波流共存这一显著特征。

基于Boussinesq方程在近岸区域实际应用的优势，美国特拉华大学建立了FUNWAVE数值模式[10]，Shi等[11]和Chen等[12]为其发展做了许多贡献。李训强等[13]使用该模式对波浪近岸传播进行了数值模拟研究，效果比较理想。本文以沿岸流物理模型的实验数据为检验资料，利用该模式计算近岸沿岸流。同时设计了沿岸流的数值模型，针对不同的波浪入射条件，对沿岸流分布特征进行分析。

1 模式介绍

1.1 控制方程

本文采用Wei等建立的Boussinesq模型[14]，在该模型的推导中，没有做弱非线性假设，保留了O(μ2)和所有阶的ε。方程形式：

(1)

(2)

式中，η是表面高度；h是静止水深；uα是水深为zα=-0.531h处水质点的水平速度矢量；=(∂/∂x,∂/∂y)为水平梯度算子；g为重力加速度；下标t是对时间的偏导。上述方程在实际应用中应增加破碎项和摩擦项等进行改进。

1.2 波浪破碎

借鉴Kennedy[15]利用动量混合方程描述浅水区域波浪破碎的能量损耗：

(3)

(4)

式中，下标x，y表示空间导数；υ是破碎波前部的局部湍黏性应力，在非线性波计算中，参数υ非常重要。

1.3 子网紊动混合

本文采用Smagorinsky型子网模型[16]来考虑涡动黏性对波生流流态的影响，其表达式为

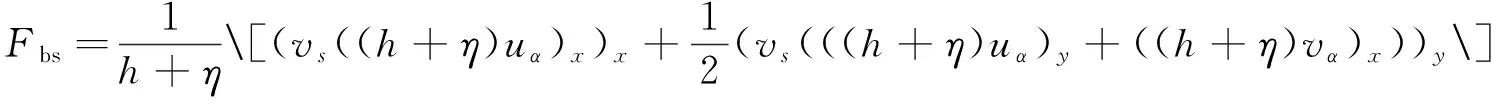
(3)

(4)

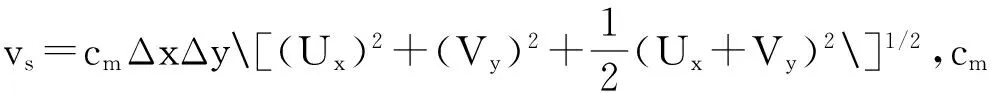
1.4 边界处理

动边界的处理方法有2种：一种是干湿网格法，一种是窄缝法[17]，本文的数值模型采用后者。窄缝法把整个计算区域作为具有窄缝或可渗透边界、可流入流出的活动型区域，将没有水或只有薄层水覆盖的固体底边界替换成可渗透的海床，或把固体海底假设具有窄缝，使得溢出的水位不会超过海滩高程。模式中设定了κ和Λ两个参数描述窄缝法对波浪计算的影响：

(7)

(8)

式中，κ是单位宽度海滩上的窄缝宽；δ是最小缝宽；λ是窄缝的形状参数；h0是窄缝起始的水深值；Λ是考虑窄缝影响后的等效水深。Madsen等对Carrier和Greeenspan的理论模型进行数值模拟[18]，发现上式中z*如果取为当地陆地高程，数值模拟的最大波浪爬高与理论解存在10%的误差。Kennedy等[15]则认为这是因为波浪上爬时首先要填满窄缝，从而引起水体质量的损失。波浪经过窄缝时，为了保持总的水体质量和没有窄缝时的水体质量相等，模式中z*表达式为

(9)

式中zs为陆地高程。

2 物理实验验证

邹志利等[19]在大连理工大学海岸和近海工程国家重点实验室的港池内进行波生流物理模型试验，实验水池部分长42.6 m，宽24.0 m。物理模型简图见图1，坡度均匀的平直海岸与造波板成30°角布置，海岸坡度为1∶100和1∶40，1∶100坡前水深为18.0 cm，1∶40坡前水深为45.0 cm。从造波机到模型的坡脚处布置了波导墙，并且在波导墙内侧放置了消浪网以防止波浪的反射。实验测量了坡度分别为1∶100和1∶40两种平直海岸上的波生沿岸流。波面升高由垂直岸线方向排列的三列电容式波高仪测量，沿岸流由应变式流速仪测量。选取如图1中所示沿岸线方向离岸距离13.0 m观测截面上的波高和流速实验值对模式进行验证。

图1 实验模型Fig.1 Diagram of the experiment setup

本文使用FUNWAVE模式对上述物理模型进行数值模拟，模式采用0.2 m×0.4 m的数值网格，造波源设置为数值模式的波浪入射边界，由于造波为双向造波，因此在造波源位置后侧设置海绵边界进行消波。斜坡上的移动边界采用上述窄缝法进行处理，为了减小FUNWAVE模式侧边界的影响，本文设置了长45.0 m，宽34.0 m的数值水槽模型，分别去除左右侧边界附近5 m的计算结果，选取数值模型中部区域的24.0 m的计算结果进行分析。由静止状态开始计算波浪运动，模式运行70 s后，波面呈现很有规律的变化，波高和流场基本稳定。选取与物理实验条件对应的一组数值模型计算结果，图2a,2b分别为波高H=0.09 m，周期T=1.0 s的规则波在1∶40平直海岸上波高和沿岸流模拟结果。图2a中，波浪波高在斜坡前变化不大，在斜坡起始线处波高分布出现变化。在岸线附近，波浪由于浅化过程出现破碎并在破碎后波高迅速衰减，辐射应力变化导致波生沿岸流的产生。图2b为数值模型计算的沿岸流分布，图中沿岸流在沿岸方向上的分布均匀合理。此外，源函数造波(计算区域左端)和海绵吸收层(计算区域左端)的处理结果比较有效。

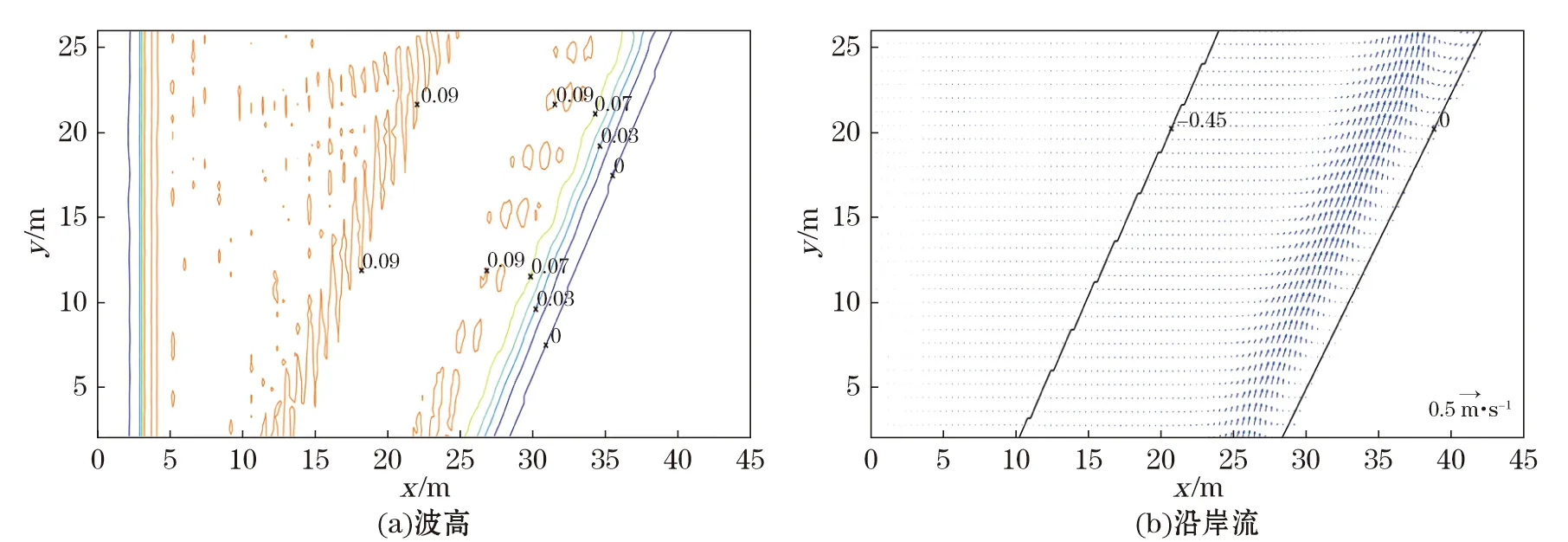
图2 FUNWAVE模拟波高和沿岸流分布Fig.2 Wave height and longshore current simulated by the FUNWAVE model

本文选取与实验观测截面一致的断面数值计算值与上述物理实验结果比较。图3为1∶100和1∶40地形下，两组入射波的波高和波生流在垂直于岸线断面上的实验观测值和数值模型计算值的比较结果。其中，图3a，图3b为1∶40坡度下，入射波高Hλ=0.09 m，周期T=1.0 s规则波的波高和沿岸流分布，图3c,3d为1∶100地形坡度下，波高为H=0.07 m，周期T=1.0 s规则波的波高和沿岸流分布。图3中，x轴为垂直岸线的水平距离，由图3可以发现，在两种坡度下，不同入射条件的波高和沿岸流数值模拟结果与实验模型的数据基本一致。在近岸区域，波浪由于浅化作用发生堆积破碎，破碎后波浪波高迅速减小。波生流的最大流速位置与波浪破碎线并不重合，而是落后于波浪破碎位置。通过图3对数值模式的验证，证明该模式可以较好地计算近岸波生流。

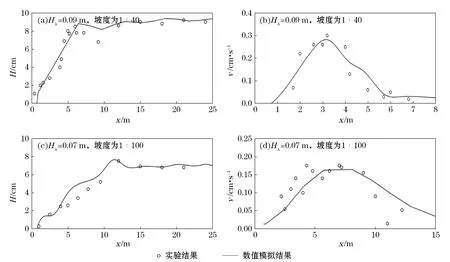
图3 数值模型和物理模型结果Fig.3 Simulated result by the FUNWAVE model versus that from experimental data

3 不同条件对波生沿岸流影响的数值分析

基于上述研究表明，FUNWAVE模式模拟近岸波生流和波高分布的效果较好。由于波生流物理模型实验的易变形性和复杂性，现采用FUNWAVE模式对不同波高、周期、坡度条件下的沿岸波生流进行数值模拟研究，从而对不同入射条件下近岸波生流的特征进行分析。

选择地形坡度1∶40进行数值实验，保持坡前水深0.45 m不变。图4a为1∶40坡度模型下，波浪入射周期T=1.0 s不变、不同入射波高条件下波生沿岸流在垂直岸线断面上计算结果。图4a中，从上往下依次为入射波高为0.13，0.11，0.09，0.07和0.05 m条件下沿岸流随离岸距离的分布。由图4a可知，当波浪的入射周期为1 s不变时，随着波浪入射波高的增大，波浪破碎线向深水处移动，波生沿岸流的幅值明显增大，沿岸流的最大值位置向深水处移动，且沿岸流的影响区域也相对增大。图4a中，波浪波高的增幅为0.02 m不变，可以发现，保持波浪波高的增幅一定，随着波高的增大，波生沿岸流的幅值及幅值的位置变化范围减小。参照上述设置，图4b为保持波浪入射波高H=0.09 m不变、不同周期下的波生沿岸流在垂直岸线断面上的数值计算结果。图4b中，3种周期条件计算的沿岸流幅值位置变化较小，随着波浪入射周期的增大，沿岸流的流幅显著变宽，幅值略微增大。周期的增加能显著改变沿岸流宽度，但对沿岸流幅值大小以及位置的影响较小。

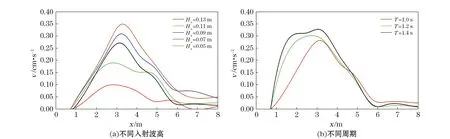
图4 不同入射波高、周期条件下波生沿岸流计算结果Fig.4 Simulated longshore current with different incident height and period

本文通过改变1∶40坡度地形下的坡前水深至0.18 m，保持其余参数不变，研究不同坡度下波生沿岸流的性质(图5)。图5为波浪入射波高Hλ=0.07 m，周期T=1.0 s不变，1∶40和1∶100两种地形坡度下，波生沿岸流在垂直岸线断面上的计算值。图5中1∶40较陡坡度下，波生沿岸流的流幅相对较小，且幅值较小。1∶40坡度下，沿岸流的幅值位置相对1∶100缓坡幅值位置向岸线偏移。通过两种坡度下幅值位置的离岸距离计算两种坡度下幅值位置的水深可以发现，1∶40和1∶100坡度下的沿岸流幅值位置附近的水深几乎相同，为0.073 m。地形坡度的变化能显著改变沿岸流的流幅和幅值，但对沿岸流幅值位置水深的影响不大。

图5 不同坡度下波生沿岸流计算结果Fig.5 Simulated longshore current with different slopes

选择1∶40坡度下，入射波高Hλ=0.09 m、周期T=1.0 s的规则波数值模型，保持其余参数不变，通过改变平直海岸与造波源的夹角，研究不同入射角条件的波生流性质(图6)。图6中，由上到下分别为夹角为30°，25°和20°条件下，波生沿岸流在垂直于岸线断面上的计算结果。图6所示，随着入射角的增大，波生流的幅值相对增大，幅值位置和流幅区向深水处偏移。

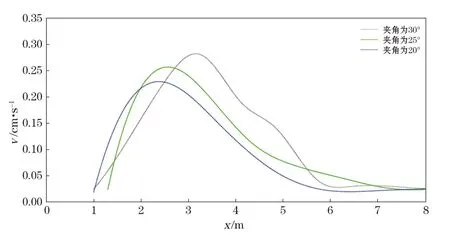
图6 不同入射角下沿岸流计算结果Fig.6 Simulated longshore current with different incident angles

4 窄缝法对沿岸流数值计算的影响

FUNWAVE模式采用窄缝法处理动边界，为了保证波浪的爬高时的水体质量守恒，在使用窄缝法处理动边界时，z*不再取值陆地高程，其取值如式(9)，从而使FUNWAVE模型计算的波浪爬高较为准确。本文在使用FUNWAVE模式计算沿岸流过程中，发现窄缝的最小缝宽(δ)和形状参数(λ)对波高和沿岸流计算的影响不大，而窄缝的起始水深值(h0)对沿岸流数值计算的影响较大，现对其进行初步讨论。

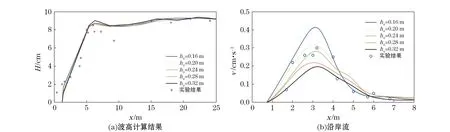
图7 不同窄缝起始水深对数值计算的影响Fig.7 Simulated wave height and longshore current with different slot depths

本文选取1∶40坡度下，波高0.09 m的规则入射波进行分析，其余设置参照上述不变。通过设置不同的窄缝起始水深，讨论不同起始水深对垂直岸线断面上的波高和沿岸流计算的影响。图7为窄缝起始水深0.16,0.20,0.24,0.28和0.32 m时，垂直岸线断面上的波高和沿岸流计算结果。图7a中，起始水深对波浪波高的计算影响较小，不同窄缝起始水深计算的波高在很小的范围内变化。图7b中，不同窄缝起始水深设置计算的沿岸流分布有较大的差异：不同窄缝起始水深下，沿岸流计算的幅值位置相对不变，幅值大小变化较大。保持窄缝起始水深变化幅度0.02 m时，沿岸流的幅值差异最大可达0.10 cm/s。通过上述讨论，采用窄缝法计算波浪波高较为精确，但在计算沿岸流时，选择合适的窄缝起始水深是十分重要的。

5 结 论

本文通过采用采用FUNWAVE模式对物理模型进行数值实验，证明FUNWAVE模式能较好的模拟近岸波生沿岸流。本文利用数值模拟耗费较少，易于调整，以及可以进行重复性实验的优势，通过斜坡地形下沿岸流的数值模拟研究，对改变单一入射条件情况的波生沿岸流进行数值模拟，得出：1)仅增大波浪的入射波高，其余入射条件不变时，波生沿岸流的幅值和流幅范围增大，幅值位置向深水移动。保持波浪波高增幅一定时，随着入射波高的增大，波生沿岸流幅值及幅值位置的变化幅度减小。2)仅增大波浪的入射周期，其余入射条件不变时，波生沿岸流的流幅显著增大。3)仅增加斜坡地形坡度，其余入射条件不变时，波生沿岸流的流幅和幅值减小，地形坡度的改变对幅值水深影响非常小。4)仅增大波浪入射角，其余入射条件不变时，沿岸流的幅值增大，且幅值位置和流幅向深水移动。

在使用FUNWAVE模式进行沿岸流计算时，窄缝法设置的起始水深对沿岸流计算有较大影响，合适的窄缝起始水深对保证流场计算的准确度时十分必要的。FUNWAVE模型的计算网格精度要求较高，对于小区域的波浪要素计算效果较好，但在计算大区域波浪传播过程，其计算量较大，耗时较长，在实际海区的流场计算时有一定的困难。

[1] SVENDSEN I A. Introduction to Nearshore Hydrodynamics[J].World Scientific Publishing Co Pte Ltd, 2006:744.

[2] SUN T, TAO J H. Numerical modelling and experimental verification of pollutant transport under waves in the nearshore zone[J].Haiyang Xuebao, 2003,25(3):104-112.孙涛,陶建华. 波浪作用下近岸区污染物输移扩散的数学模型及其实验验证[J].海洋学报,2003,25(3):104-112.

[3] REN C P, ZOU Z L. Research development of the shear instability of longshore current[J].Marine Science Bulletin, 2010,29(5):588-593.任春平,邹志利.沿岸流不稳定运动研究进展[J].海洋通报,2010,29(5):588-593.

[4] BIRKEMEIER W A, DONOGHUE C, LONG C E, et al. 1990 DELILAH nearshore experiment: Summary Report[R].Delilah Nearshore Experiment Summary Report, 1997.

[5] CHOI J, KIRBY J T, YOON S B. Boussinesq modeling of longshore currents in the SandyDuck experiment under directional random wave conditions[J].Coastal Engineering, 2015,101:17-34.

[6] HAAS K A, WARNER J C. Comparing a quasi-3D to a full 3D nearshore circulation model: SHORECIRC and ROMS[J].Ocean Modelling, 2009,26(1-2):91-103.

[7] TANG J, SHEN Y, QIU D. Numerical study of pollutant movement in waves and wave-induced long-shore currents in surf zone[J].Acta Oceanologica Sinica, 2008,27(1):122-131.

[8] FANG K Z, ZOU Z L, LIU Z B. Numerical simulation of rip current generated on a barred beach[J].Chinese Journal of Hydrodynamics, 2011,26(4):479-486.房克照,邹志利,刘忠波.沙坝海岸上裂流的数值模拟[J].水动力学研究与进展,2011,26(4):479-486.

[9] LI S W, HUANG X Y. Numerical method for calculation of longshore current by using Boussinesq equations[J].Journal of Tianjin University.2004,37(12):1059-1062.李绍武,黄筱云.用Boussinesq方程计算沿岸流的数值方法[J].天津大学学报:自然科学与工程技术版,2004,37(12):1059-1062.

[10] KIRBY J T, WEI G, CHEN Q, et al. FUNWAVE 1.0, fully nonlinear Boussinesq wave model documentation and user's manual[J].University of Delaware, 1998.

[11] SHI F, DALRYMPLE R A, KIRBY J T, et al. A fully nonlinear Boussinesq model in generalized curvilinear coordinates[J].Coastal Engineering, 1999, 42(4):337-358.

[12] QIN C, JAMES T K, DALRYMPLE R A, et al. Boussinesq modeling of wave transformation, breaking, and runup. II: 2D[J].Journal of Waterway Port Coastal & ocean Engineering, 2000,126(1):39-47.

[13] LI X Q, YANG J X, ZHU S X, et al. Numerical simulations of surfing waves on mild slopes[J].Advance in Marine Science,2015,33(2):155-163.李训强,杨家轩,朱首贤,等.缓坡地形拍岸浪数值模拟研究[J].海洋科学进展,2015,33(2):155-163.

[14] WEI G, KIRBY J T, GRILLI S T, et al. A fully nonlinear Boussinesq model for surface waves. I. Highly nonlinear, unsteady waves.[J].Journal of Fluid Mechanics, 1995,294:71-92.

[15] KENNEDY B, CHEN Q, KIRBY J T, et al. Boussinesq modeling of wave transformation, breaking, and runup. I: 1D[J].Journal of Waterway Port Coastal & Ocean Engineering, 2002,126(1):39-47.

[16] SMAGORINSKY J. General circulation experiments with the primitive equations[J].Monthly Weather Review, 1963,91(3):99-164.

[17] MADSEN P A, MURRAY R. A new form of the Boussinesq equations with improved linear dispersion characteristics[J].Coastal Engineering, 1991,15(4):371-388.

[18] CARRIER G F, GREENSPAN H P. Water waves of finite amplitude on a sloping beach[J].Journal of Fluid Mechanics, 1958,4(1):97-109.

[19] ZOU Z L, CHANG M, QIU D H, et al. Experimental study of longshore currents[J].Journal of Hydrodynamics, 2002,17(2):174-180.邹志利,常梅,邱大洪,等.沿岸流的实验研究[J].水动力学研究与进展, 2002,17(2):174-180.

Received: December 2, 2015

Numerical Simulation of Longshore Currents Induced by Waves

WANG Hong1,LI Xun-qiang1,ZHU Shou-xian2,ZHANG Wen-jing1

(1.InstituteofMeteorologyandOceanography,PLAUniversityofScienceandTechnology, Nanjing, 211101, China；2.InstituteofOceanography,HohaiUniversity, Nanjing 210098, China)

The FUNWAVE model based on nonlinear Bosssinesq equations is employed to simulate the longshore current induced by waves. Comparison with the experimental results of physical model show that the FUNWAVE model can well simulate the longshore currents. The model is further employed to the simulate longshore current on different slopes, with varying heights and periods, and results show that when incident height or period increases, the magnitude and width of the longshore current will also increase, and the location of maximum longshore current moves towards deeper water as incident height increases. When terrain slope changes, the magnitude and width change significantly but the location of maximum longshore current does not change. FUNWAVE model adopts slot technique to deal with transient boundary, the initial depth of slot technique has an important impact on the longshore current simulation.

longshore current; numerical simulation; Boussinesq equation; slot technique

2015-12-02

国家自然科学基金项目——引入波浪漫滩边界的近岸海域悬沙输运数值模式及其应用(41076048)；中央高校基本科研业务费专项项目——流和温盐垂向异结构的新型海洋模式研制及其应用(2011B05714)

汪 鸿(1992-)，男，硕士研究生，主要从事海洋数值模拟方面研究.E-mail：wanghong_92@126.com

*通讯作者：李训强(1962-)，男，江苏睢宁人，副教授，硕士研究生导师，主要从事海洋动力学与数值模拟方面研究.E-mail：lixunqiang@sina.com

P731

A

1671-6647(2016)04-0507-09

10.3969/j.issn.1671-6647.2016.04.006