狭长空间环境下改进的WSN节点质心定位算法

赵志信， 李加君， 江晓林， 谢玉鹏

(黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022)



狭长空间环境下改进的WSN节点质心定位算法

赵志信， 李加君， 江晓林， 谢玉鹏

(黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022)

针对狭长空间环境下信号传播的多径效应等原因导致节点定位的精度不足问题，提出一种改进的WSN(无线传感器网络)节点质心定位算法。首先，给出狭长空间环境下锚节点部署策略，采用shadowing模型将锚节点接收到的信号强度值转换为距离值,使得未知节点的位置初步定位在最近的三个锚节点构成的三角形内；然后，以这三个锚节点的圆心距离值为半径形成三个圆，根据得到的有效交点个数，分四种情况得到未知节点的位置估计。仿真结果表明，改进质心算法平均定位误差在1 m左右，在定位区域不同位置仍能保持稳定的定位性能，与极大似然估计法和质心算法相比，该算法定位精度与稳定性都得到提高。

多径效应； 锚节点； 定位； 狭长环境； 质心算法

0 引 言

无线传感器网络由大量的微型传感器节点组成，并通过无线通信方式形成一个自组织的智能网络系统，能够实时监测监控区域内的各种环境信息，同时对这些信息进行处理并传输[1-3]。WSN节点定位是无线传感器网络关键支撑技术。在狭长空间环境下的WSN节点定位对于煤矿井下应急救援，以及楼层走廊的消防救援等，有着重要的现实的意义。

根据是否需要测量实际节点间的距离，将定位算法分为基于测距(range-based)和与距离无关(range-free)两种定位算法。两者间的区别在于是否需要测量相邻节点间的实际距离。基于测距的定位算法需要额外的硬件来协助定位，成本要高于与距离无关的定位算法，但是在精度与效率上，前者要优于后者。

基于测距的定位算法中，基于接收信号强度指示(RSSI)[4]的定位，通过接收端接收的信号衰减估算节点间的距离，但是由于环境的不同，衰减系数也有所差异，导致定位存在较大误差。

不需要测距的定位算法中，三角形内点近似估计法(APIT)[5]通过判断移动节点是否在锚节点形成的三角形内进行定位，由于该算法要求节点一直处于移动当中，因此在实际应用中不是很灵活。质心算法[6]是通过计算锚节点形成的多边形的质心坐标来进行定位。针对狭长空间环境下信号传播的多径效应导致节点定位精度不足的情况，笔者提出一种改进的WSN节点质心定位算法。给出狭长空间环境下锚节点部署策略，采用shadowing模型将锚节点接收到的信号强度值转换为距离值,使得未知节点的位置初步定位在最近的三个锚节点构成的三角形内；然后以这三个锚节点为圆心距离值为半径形成三个圆，根据得到的有效交点个数，分四种情况得到未知节点的位置估计。

1 算法模型

1.1 锚节点部署模型

在无线传感器网络中，每种定位算法都有其特定的应用环境， 文中算法主要针对狭长空间环境下的未知节点进行定位。为了节约网络成本，以较少的锚节点覆盖整个狭长空间，将锚节点均匀地部署在狭长空间两侧，且距离相等，未知节点可位于定位区域内任意一点。锚节点部署模型如图1所示。在定位过程中，未知节点向通信范围内的锚节点发出一个包含自身ID的信息包，锚节点将接收到的信号强度值换算成距离值之后，转发给汇聚节点，由汇聚节点进行比较计算，给出未知节点的位置估计。

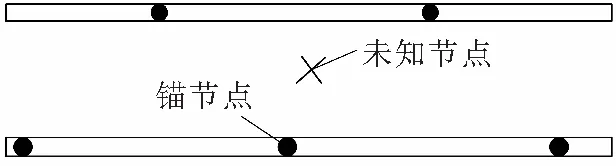
图1 锚节点部署模型

1.2 理论传播模型

已知发送信号的强度，通过测量接收信号强度，计算信号的传播损耗，根据理论或经验信号传播衰减模型将传播损耗转化为距离。得到锚节点与未知节点之间的距离信息。

在实际狭长空间环境定位中，shadowing模型[7-9]更符合实际环境，shadowing模型分为两部分，第一部分为路径损耗模型：

pr(d0)/pr(d)=(d/d0)n,

(1)

式中:pr(d0)——参考距离d0处的接收信号强度；

pr(d)——距离d时接收到的平均功率；

n——信号传播路径衰落系数。

Shadowing模型的第二部分，表示在同一距离上接收到的信号能量满足高斯分布，即

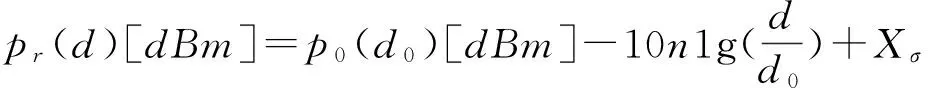
(2)

式中:Xσ——由阴影效应引起的正态分布的随机变量。

2 算法描述

2.1 算法思想

未知节点向通信范围内的锚节点发送信号，锚节点通过shadowing模型将接收到的信号强度转换为距离值，找出距离未知节点最近的三个锚节点a、b、c(对应的到未知节点的距离分别为r1、r2、r3)。以锚节点为圆心，距离r1、r2、r3为半径形成三个圆，根据得到的有效交点(位于定位区域内的交点)个数，对未知节点的定位分为以下四种情况：

(1)当交点数为1时，则以此交点作为未知节点的坐标；

(2)当交点数为2时，则取两交点连线的中点作为未知节点的坐标；

(3)当交点数为3或5时，则取3个交点构成的三角形或5个交点构成的多边形的质心作为未知节点的坐标；

(4)当交点数为4时，交点D、E、F、G将三圆交叉区域分为2个三角形DEF和三角形GEF，最后取面积稍小的三角形DEF的质心作为未知节点的坐标，原理如图2所示。

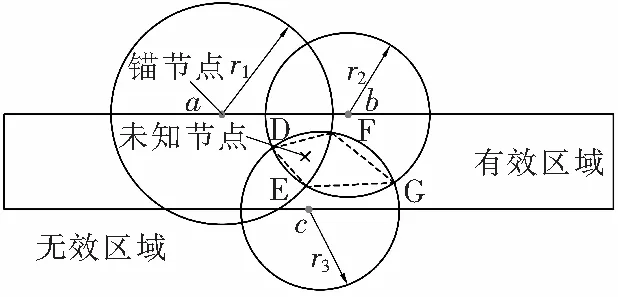
图2 有效交点为4时的算法定位原理

Fig. 2 Positioning principle of algorithm with effective intersection four points

2.2 算法实现

具体的定位过程可以分为以下几个步骤：

(1) 接收信号强度值的采集与换算：通过式(3)计算锚节点与未知节点之间的距离：

d=d0×10[p0(d0)-pr(d)-Xσ]/10n。

(3)

(2) 寻找最近的锚节点：比较未知节点到不同锚节点的距离值，找出距离未知节点最近的三个锚节点。

(3) 计算有效区域内的交点：以这3个锚节点为圆心，距离值为半径形成的3个圆，利用式(4)分别计算处于有效区域内每两个圆的交点，

(4)

式中：(x,y)——交点坐标；

(xi,yi)、(xj,yj)——锚节点i和锚节点j的坐标；

di、dj——未知节点到锚节点i和j距离，i,j=1,2,3,i≠j。

(4) 根据有效交点数的不同，对未知节点定位。定位方法分为以下四种情况：

(a)当有效交点数为1时，则以此交点作为未知节点的坐标；

(b)当有效交点数为2时，则取两交点连线的中点作为未知节点的坐标；

(c)当有效交点数为3或5时，则取3个交点构成三角形或5个交点构成的多边形的质心作为未知节点的坐标，利用式(5)计算质心坐标：

(5)

式中:i——有效交点个数；

(X，Y)——质心坐标；

(xi，yi)——有效交点坐标。

(d)当交点数为4时，则寻找最小三角形：以中间两个交点的连线为公共边，将三圆交叉区域分为两个三角形，分别计算公共边两侧的交点到该公共边的距离，距离值较小的点和中间两个交点形成的三角形面积最小，取该三角形的质心作为未知节点的坐标。公共边两侧的交点到公共边的距离D为

(6)

式中：y=kx+b——中间两交点的连线方程；

(x0,y0)——公共边两侧任意一交点的坐标。

3 仿真结果与分析

仿真实验在Matlab R2014a上进行。在30 m×5 m的狭长空间的两侧均匀部署9个锚节点，通过shadowing模型计算距离值时，随机变量为均值0,方差0.5的高斯随机变量。

仿真过程中锚节点个数不变，随机产生10个未知节点进行定位，图3为采用改进质心算法得到的10个未知节点的位置估计。由图3可知，改进质心算法的定位误差较小。

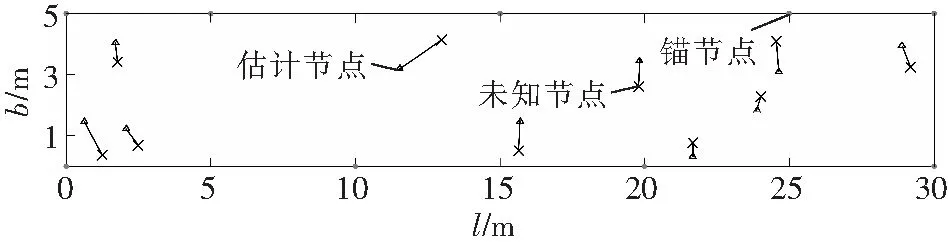
图3 10个未知节点分布

图4给出了定位区域内不同位置的定位误差，显示了定位误差e在定位空间不同位置的变化情况。如图4所示，在定位区域内不同位置下的定位误差波动很小。结果表明，改进质心算法在狭长空间环境下的不同位置，仍能保持高的定位精度和稳定的定位性能。

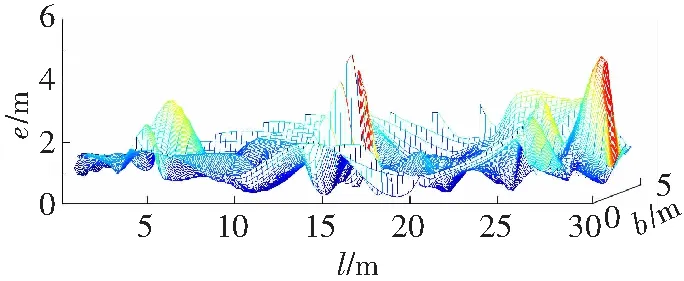
图4 改进质心算法在不同位置上的定位误差

Fig. 4 Location error of improved centroid algorithm in different position

为了降低未知节点在定位区域随机分布对仿真结果带来的影响，仿真中，分别对10个未知节点的位置进行1 000次估计，取定位误差的平均值ev，改进质心算法、极大似然算法[10]和质心算法的平均误差曲线如图5所示。由图5可知，改进质心算法的平均误差为1 m左右，定位精度以及稳定性都要优于极大似然估计法和质心算法。

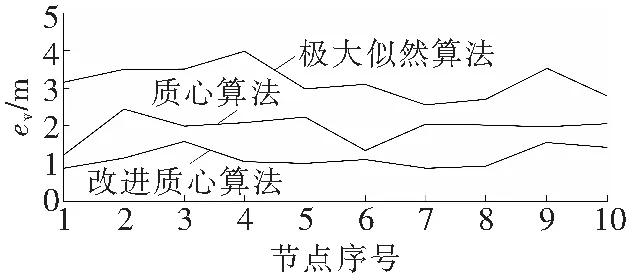
图5 平均误差曲线

4 结束语

笔者提出一种狭长空间环境下改进的WSN节点质心定位算法。该算法首先通过shadowing模型将接收到的信号强度值转换成距离值，再根据距离值找出距离未知节点最近的三个锚节点；然后，以这三个锚节点为圆心距离值为半径形成三个圆，根据得到的有效交点个数，分四种情况得到未知节点的位置估计。仿真结果表明，改进质心算法定位误差约1 m，且在定位区域内不同位置下的定位误差波动很小，在狭长空间环境下具有较高且平稳的定位精度，与极大似然估计法和质心算法相比较，改进的质心算法的定位精度要优于两者，证实了该算法的可行性与有效性。

[1] LI J, ZHONG X, LU I. Three-dimensional node localization algorithm for WSN based on differential RSS irregular transmission model [J]. Jounal of Communications, 2014, 9(5): 391-397.

[2] ZHANG Z, XU X, YAN L. Underground localization algorithm of wireless sensor network based on Zigbee [J]. Journal of China Coal Society, 2009, 34(1): 125-128.

[3] 陈 敏, 王 擘, 李军华， 等. 无线传感器网络原理与实践[M]. 北京: 化学工业出版社, 2011: 1-7.

[4] 章 磊， 黄光明. 基于RSSI的无线传感器网络节点定位算法[J]. 计算机工程与设计， 2010, 31(2)： 291-294.

[5] DARGIE W, POOLLABAUER C. Fundamentals of wireless sensor networks: theory and practice [M]. Singapore: Markono, 2010: 259-260.

[6] 许红艳， 王经卓， 董自健, 等. 无线传感器网络节点定位算法的改进[J]. 微计算机信息, 2012, 28(10)： 303-305.

[7] WANG Y. A research on the localization technology of wireless sensor net works [D]. Hefei： University of Science and Technology of China, 2007.

[8] 乔钢柱，曾建潮. 信标节点链式部署的井下无线传感器网络定位算法[J]. 煤炭学报， 2010, 35(7): 1229-1223.

[9] 方 震, 赵 湛, 郭 鹏, 等. 基于RSSI测距分析[J]. 传感技术学报, 2007, 20(11): 2526-2530.

[10] 李建坡, 钟鑫鑫, 徐 纯. 无线传感器网络动态节点定位算法综述[J]. 东北电力大学学报， 2015, 35(1): 52-58.

(编辑 晁晓筠 校对 李德根)

Improved WSN node centroid localization algorithm in long and narrow space environment

ZhaoZhixin,LiJiajun,JiangXiaolin,XieYupeng

(School of Electronics & Information Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

This paper proposes an improved node centroid localization algorithm based on WSN as a solution to insufficient accuracy of sensor node positioning due to signal multipath effect result in narrow space. The study consists of providing a strategy of node deployment in narrow space, converting received signal strength value of anchor node to distance value, and leaving the unknown node primarily mapped in a triangle consisting of the nearest three anchor node; and then taking the three anchor node as the center and a radius of distance value to form three circles and dividing the position estimation of unknown nodes into four cases based on the number of effective cross points. Simulation results show that the improved algorithm working with a positioning error of around 1 m, boasts a higher positioning accuracy and stability than the maximum likelihood estimation method and the centroid algorithm.

multipath effect; anchor node; positioning; narrow space; centroid algorithm

2016-09-02

黑龙江省自然科学基金面上项目(F2015019;F2015017)

赵志信(1979-)，男，黑龙江省依兰人，副教授，博士，研究方向：无线网络资源管理，E-mail：zhaozhixin0830@163.com。

10.3969/j.issn.2095-7262.2016.05.022

TN914.5

2095-7262(2016)05-0577-04

A