带有等相关误差结构生长曲线模型的参数boo tstrap检验
2016-12-09徐礼文瞿开毅
徐礼文,瞿开毅
(1.中国人民大学统计学院,北京100872;2.北方工业大学理学院,北京100144)
带有等相关误差结构生长曲线模型的参数boo tstrap检验
徐礼文1,2,瞿开毅2
(1.中国人民大学统计学院,北京100872;2.北方工业大学理学院,北京100144)
文章研究了具有等相关误差结构的生长曲线模型回归系数的检验问题,构造了参数bootstrap(PB)检验统计量和相应的PB检验,并与已有的广义p值(GP)检验进行了比较。模拟研究表明,PB方法和GP方法在单处理组情形下的表现趋于一致,均能很好的控制第一类错误率;在多处理组情形下,GP方法在一些情形下不能很好地控制犯第一类错误的概率,而PB方法则在很好地保证检验名义水平的前提下,同时也具有良好的势表现。
生长曲线模型;重复观测;bootstrap重抽样;广义p值
0 引言
生长曲线模型在生物学、医药学、社会经济学、心理学等领域具有非常广泛的应用,许多学者对该模型进行了大量研究[1-4]。由于生长曲线模型用于建模重复观测的数据,且模型协方差矩阵因包含方差分量通常未知,传统检验方法大多基于近似理论,难以得到精确检验。Weerahandi和Berger[5]提出运用广义p值(GP)方法构造了具有误差独立结构的简单生长曲线模型回归系数的精确检验。Lin和Lee[6]进一步研究了等相关误差结构的生长曲线模型回归系数的广义p值检验。其中文献[5,6]所说精确性其实是指广义p值的计算公式是有精确表达式的。但广义p值和经典p值的定义却有很大差异,有时无法保证经典p值检验的优良性。
大量的研究表明,bootstrap方法在检验问题中具有维持名义水平的优良性质,在许多情形下要优于GP方法[7-9]。而鲜有学者研究生长曲线模型回归系数检验问题中两种方法的优良性比较。因此本文针对回归系数检验问题构造了参数bootstrap(PB)检验,并与GP方法进行比较研究。
1 单处理组生长曲线模型回归系数的单边检验
单处理情形生长曲线模型的一般形式为:

其中,Yit表示因变量在第i个体第t个时刻的观测,Xt是协变量向量,β为相应的回归系数,αi和εit分别表示个体随机效应和随机误差项。其矩阵表达式为:

该协方差矩阵具有等相关结构。在该协方差阵结构下,可以证明回归系数的广义最小二乘估计和普通最小二乘估计是相同的[10],也是此模型下最大似然估计。模型(2)的最小二乘估计为
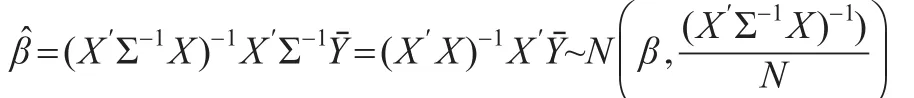
1.1GP检验


(bk,ssw,ssb)表示的一组样本观测,TGP的样本观测值T0=bk-βk,与除检验参数外的其他讨厌参数无关。因此,广义p值可表示为:

1.3PB-S检验

2 多处理组生长曲线模型回归系数的相等性检验
上文讨论了只包含单个处理组时生长曲线模型回归系数的检验问题,下面考虑包含多个处理组时生长曲线模型回归系数的相等性检验,即H0:β1=…=βm.考虑的模型一般形式为:

αij和εijt分别为个体随机效应和随即干扰项。其矩阵形式为:

2.1广义F(GF)检验
对于模型(8),称协方差矩阵Σi不相等的情形为异方差。模型的残差平方和为其中


且有:


eij~N(0,IT).令为原假设下的标准化残差平方和,为备择假设下的标准化残差平方和。对于检验H0:β1=…=βm的广义检验变量为:

其中,


2.2PB-F检验
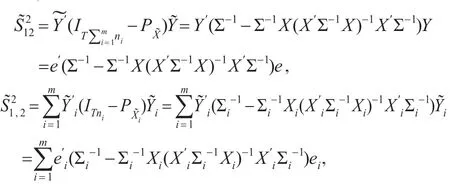
于是,PB-F检验统计量为:

3 随机模拟研究
为了比较参数bootstrap方法与广义p值方法在上述不同情形下的优良性,我们采用Monte Carlo方法进行模拟研究。具体地,分别模拟两种检验方法对于检验问题的第一类错误概率和势函数。为了便于模拟,对模型作如下假定
3.1单处理组回归系数的模拟检验
考虑β2及线性组合β2+β3的单边检验。设定回归系数的真值为β=(10,2,1)′,模拟模型在不同样本量n和不同组合情形下的第一类错误率和势函数的表现。现给出单个β2的PB-S检验的p值算法如下:
内循环:l=1 to L;
(4)利用(6)式计算TBS.如果TBS>T0,记countl=1;否则记为0;
结束内循环;
检验的势可通过类似的算法得到。考虑到该模拟涉及到内外两层循环,本文设定内循环和外循环的次数为(L,M)=(3000,2000)。计算过程是在SAS软件环境下进行的。第一类错误概率和检验势的模拟结果分别见表1和表2。

表1 单处理组情形下回归系数的第一类错误概率的估计值
从表1的第一类错误率估计中可以看出,两种方法在各种情形下都能很好的控制第一类错误概率;而从表2可以看出,两种方法的检验势表现基本一致。值得注意的是,在不同的组合情形下,两种方法的检验势差别较大。

表2 单处理组情形下回归系数的检验势的估计值
3.2多处理组的回归系数的相等性检验模拟比较
对于含3个处理组的生长曲线模型,我们模拟比较GF和PB-FS三种方法在不同样本组合和不同协方差矩阵情形下的第一类错误率和检验势表现。PB-FS方法的p值算法如下:
循环:for i=1 to L;
(3)根据(13)式计算TPB-F,若TPB-F>T0,记counti=1;否则记为0;
(4)即为p值的估计值;
与单处理组类似,假定回归系数向量的真值为β1=β2=β3=(10,2,1)′,设定内循环和外循环的次数为(L,M)=(3000,2000).并且在检验势的模拟中,为了便于比较,保持回归系数向量βi的第一和第三分量不变,仅改变第二分量。检验的模拟结果如表3和表4。
从表3可看出,当样本量非单调、三个处理组随机误差项的方差相差较大时,GF方法的第一类错误率显著大于0.05,尤其当样本量=(8,4,6)时,GF的第一类错误率达到0.08,表现出一定的随意性;而PB方法在各种情形下均表现稳定。

表3 多处理组回归系数相等性检验的第一类错误率估计

表4 多处理组回归系数相等性检验势估计
从表4可看出GF方法在样本量非单调、三个处理组随机误差项的方差相差较大时,GF的检验势显著大于PF-F方法,其原因是此情形下具有较高的第一类错误率。在其他情形下,两种方法的检验势趋于一致。综上分析,PB-F方法表现较为稳定,而GF方法在一些情形下表现过于自由。
4 结论
当考虑多个处理组的生长曲线模型回归系数相等性比较时,广义p值检验无法控制第一类错误的问题没有受到足够重视。本文从单处理组和多处理组两方面分别比较了参数bootstrap方法(PB)和广义p值方法(GP)在生长曲线模型回归系数检验的功效表现。模拟结果表明,两种方法在单处理组情形下的表现是较为一致的,均能很好的控制第一类错误率;而在多处理组情形下,当样本量非单调、处理组随机误差项的方差相差较大时,GP方法无法保证名义水平,第一类错误率偏高,而PB方法在各种情形表现更加稳健,且具有良好势的表现。
[1]Rao CR.Comparison ofGrowth Curves[J].Biometrics,1958,(14).
[2]Kshirsagar A M,Smith W B.Growth Curves[M].New York,Dekker, 1995.
[3]Pan J,Fang K.Growth Curve Models and Statistical Diagnostics[M]. New York:Springer-Verlag,2002.
[4]Ratan D.Advances in Growth Curve Models:Topics From the Indian Statistical Institute[M].New York:Springer,2013.
[5]Weerahandi S,Berger VW.Exact Inference for Growth CurvesWith IntraclassCorrelation Structure[J].Biometrics,1999,(55).
[6]Lin SH,Lee JC.Exact Tests in Simple Growth Curve Models and One-way ANOVAWith Equicorrelation Error Structure[J].Journal of Multivariate Analysis,2003,(84).
[7]Krishnamoorthy K,Lu F,Mathew T.A Parametric Bootstrap Ap⁃proach for ANOVAWith Unequal Variances:Fixed and Random Mod⁃els[J].ComputationalStatistics&Data Analysis,2007,(51).
[8]Krishnamoorthy K,Lu F.A Parametric Bootstrap Solution to the MANOVA Under Heteroscedasticity[J].J.Stat.Comput.Simul.2010,(80).
[9]Xu LW,Yang FQ,Abula A,et al.A parametric Bootstrap Approach for Two-Way ANOVA In Presence of Possible InteractionsWith Un⁃equalVariances[J].JournalofMultivariate Analysis,2013.
[10]Rao CR.Least-Squares Theory Using an Estimated Dispersion Ma⁃trix and Its Application To Measurement of Signals[C].Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability,1967,(1).
(责任编辑/易永生)
0212
A
1002-6487(2016)19-0027-05
国家自然科学基金资助项目(11171002);北京市属高等学校高层次人才引进与培养计划项目(CIT&TCD201404002);北京市自然科学基金资助项目(9144026)
徐礼文(1977—),男,安徽滁州人,博士,教授,研究方向:复杂数据分析。
