一种改进的电子情报分析模型*

张强，王红卫，陈游，徐源

（空军工程大学航空航天工程学院，西安710038）

一种改进的电子情报分析模型*

张强，王红卫，陈游，徐源

（空军工程大学航空航天工程学院，西安710038）

电子情报的分析处理，对提高电子对抗作战效能意义重大。综合运用聚类算法和分类算法构建了一种改进的电子情报分析模型。该模型首先通过基于粗糙集改进的k-means算法完成对记录数据库中雷达信号的聚类分选，选取聚类中心信号表征此类信号；再采用粗糙集提取有效的最优规则并用于聚类中心脉冲识别，从而分选出已知信号和未知信号；未知信号确定其特性后添加到已知威胁雷达数据库。通过仿真，验证了该模型的适用性和有效性。

电子对抗，电子情报，k-means算法，粗糙集

0 引言

电子对抗经过近半个世纪的发展，已经成为空中作战的重要战斗力［1］，也就此奠定了夺取制空权必先取得制电磁权的现代化高新技术战争格局，制电磁权的基础是电子情报的侦察与分析。电子情报在保持防御能力和防止突袭方面具有十分重要的意义。本文的电子情报指对雷达系统发射的信号进行观测的结果，目的是获得有关雷达的各类信息［2］。

目前作战飞机大都具备了较强的记录情报能力，可以通过电子情报侦察将战场内的空中电磁信息记录下来，为地面人员进一步分析敌情提供第一手情报资料［3］。电子情报侦察设备将接收到的雷达信号的载频（RF）、脉冲到达时间（TOA）、脉冲到达角（AOA）、脉冲重复频率（PRF）、脉宽（PW）、脉冲幅度（PA）等特征参数存储到记录数据库中，也可以对全脉冲数据进行记录。飞机完成任务后，将记录数据库中的情报参数卸载下来，基于存有敌方雷达情报参数的已知威胁雷达数据库进行相关分析，分选和识别出已知信号和未知信号。未知信号作为新的威胁信号，需要通过分析并和其他情报进行相关、对比、印证等，确定特性后，输出相关的全部参数以及处理的结果文件，并添加到已知威胁雷达数据库中，便于下次作战中对敌方目标的分选和识别［4］。

面对日益复杂的电磁环境和迅猛发展的雷达技术，原有的电子情报分析技术已经很难满足作战需要。如今，数据挖掘中的聚类算法和分类算法普遍运用于电子情报分析［5-6］，但面对当前错综复杂的电磁环境，由单一的聚类算法或者分类算法组成的旧有模型已经无法准确高效地对电子情报进行分析［7-8］，因此，本文综合运用聚类算法和分类算法构建了一种改进的电子情报分析模型，首先使用粗糙集改进的k-means算法对记录数据库中的复杂雷达信号进行聚类分选，采用聚类中心表征该类雷达信号，然后采用粗糙集对其进行分类识别，进而发现未知雷达信号。经过仿真，验证了改进模型能够准确高效地应用于电子情报分析。

1 改进的电子情报分析模型

电子情报分析模型主要用于从记录数据库中发现危险未知雷达信号，确定其特性后添加到已知威胁雷达数据库中，以便于下次作战。改进的模型如图1所示。首先通过基于粗糙集改进的k-means算法完成对记录数据库中雷达信号的聚类分选，得到聚类个数和聚类中心，选取聚类中心信号表征此类信号；再采用粗糙集分析已知威胁雷达数据库中雷达信号数据之间的联系，获得其中的重要知识。通过连续属性离散化、属性约简和规则提取，提取出最优规则并用于聚类中心信号识别，从而甄选出已知信号和未知信号，并对未知信号进行相关处理，确定其特性后添加到已知威胁雷达数据库中。

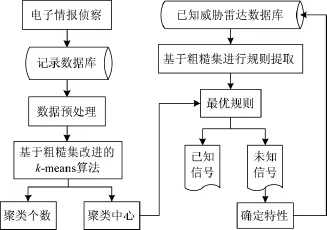
图1 改进的电子情报分析模型

2 基于粗糙集改进的k-means算法

k-means算法是经典的划分聚类算法［9］，普遍应用于雷达信号的聚类分选，但k-means算法应用时存在以下局限：①关于k值的确定。在k-means算法中，必须事先人为确定聚类数目k，k值选择的恰当与否，直接影响聚类结果；②复杂雷达信号的特性。面对高密度、分离性差的复杂雷达信号，k-means算法无法进行有效的聚类分选。为了克服以上局限，采用粗糙集［10-12］的思想改进k-means算法。

粗糙集思想是通过上近似集和下近似集的概念来表示某对象属于某类的特点。上近似集和下近似集满足如下基本性质：

①对象xi属于一个类的下近似集，那完全属于此类，若属于一个类的上近似集，那可能属于此类；

②对象xi只能属于一个类的下近似集，若属于一个类的下近似集，那同时也属于该类的上近似集；

③对象xi不属于任何类的下近似集，那属于两个或多个类的上近似集。

粗糙集是利用上近似集和下近似集的概念解决了类与类之间边界不清晰的问题，从而克服了传统k-means算法无法对复杂雷达信号进行有效聚类分选的局限，同时也可以动态地确定聚类数目k，具体思路如下：

①若一个类的下近似集对象个数为0，则该类下近似集无存在必要，所以类数减1；

②若两个类的上近似集对象相同，则两个类相似度高，可以合并为一个类，所以类数减1。

基于粗糙集改进的k-means算法聚类中心为

式中：vi表示聚类中心，wupper表示上近似集权重，wlower表示下近似集权重，且wupper+wlower=1。因为下近似集是上近似集的子集，故wlower≥wupper。（C）表示类C的上近似集，A（C）表示类C的下近似集。Nupper表示第i个类中的上近似集的对象个数，Nlower表示第i个类中的下近似集的对象个数。

基于粗糙集改进的k-means算法的步骤如下：

Step 2：通过使用k-means算法进行初步聚类，得到k个聚类中心，并据此结果计算距离判断阈值rt；

Step 3：采用加权欧式距离计算方法依次计算每个对象与各聚类中心之间的距离，取与各聚类中心之间的最小距离记作rmin和次小距离记作rs-min，将当前对象归入与其取距离最小的类中，rs-min-rmin≥rt，将该对象归入与其取距离最小的类的上近似集；若rs-min-rmin＜rt，则归入该类的下近似集，并使用上述的聚类中心公式更新聚类中心；

Step 4：利用上近似集和下近似集的概念动态地确定聚类数目k：若两个类的上近似集相同，则合并这两类，k=k-1；若某个类的下近似集为空，则删除该类，k=k-1；

Step 5：重复Step3和Step4直至k值不再发生变化，输出合理聚类数目k和聚类中心。

3 基于粗糙集的雷达信号识别

基于粗糙集的雷达信号识别基本思想：采用粗糙集分析已知威胁雷达数据库中雷达信号数据之间的联系，获得其中的重要知识及关键信息，提取出有效的最优规则，并将其应用于待识别雷达信号（聚类中心信号）的识别。

3.1雷达信号识别模型

若已知威胁雷达数据库中已知m种雷达，每种雷达又具有n种不同的工作模式。将雷达信号特征参数视为条件属性，则条件属性集为C={c1，c2，…，cl}，约简集为C*。将雷达信号类别视为决策属性，则决策属性集D={d1，d2，…，dm}。已知电子情报数据库为论域U={u1，u2，…，un}，其中一条样本雷达信号为ut={c1，c2，…，cl，t；dt}，其属性值为：ci（ut）=ci，t（i=1，2，…，l；t=1，2，…，n），d（ut）∈D。此时，由ut（t=1，2，…，n）构成的二维信息表即为雷达信号识别的关系数据模型，即S=（U，C|D）。

3.2连续属性离散化

粗糙集不能对连续属性进行处理，只能处理离散的属性值，因此，在进行属性约简和规则提取前，必须对连续属性值进行离散化处理。本文结合雷达识别的背景和现实作战的要求，选用等间隔法对连续属性值进行离散化处理。

3.3属性约简和规则提取

利用DMRM法从决策表中提取关于属性值区分的属性，进而构造区分函数，用以属性约简和属性值约简［13］。具体的算法如下：①删去决策表中重复属性的对象xi；②从决策表中提取每个对象关于属性值区分的属性，并构造区分函数f（k），同时利用吸收率约去多余的项；③求f（k）最小析取范式，得到核属性core（C）；④从f（k）中消去可约属性，并求出其最小析取范式f'（k），得到该对象对应的属性值约简，并由单元数范式找出核属性；⑤根据上一步结果求得包含所有约简决策规则的决策表；⑥约去所有过剩规则得到包含最小规则集的决策表；⑦提取规则集，根据核值表和原来的样本列出可能性决策表。

基于粗糙集的雷达信号识别流程图如图2所示。

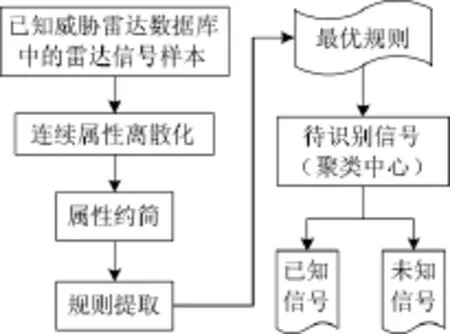
图2 基于粗糙集的雷达信号识别流程图

4 仿真分析

仿真主要思路：①通过基于粗糙集改进的k-means算法对记录数据库中的雷达信号数据进行聚类实验，得到聚类个数和聚类中心；②运用粗糙集从已知威胁雷达数据中提取最优规则并用于聚类中心信号识别，从而发现未知雷达信号。设雷达信号特征矢量由载频（RF）、脉冲重复频率（PRF）、脉宽（PW）3个特征参数组成。

4.1基于粗糙集改进的k-means算法聚类结果分析

为了能够对聚类结果进行有效评价，实验采用已知的人工数据，构造了50条由RF、PRF、PW组成的4类符合雷达实际工作情况的雷达信号数据，并人工标注其序号和类别信息，将其作为记录数据库中的雷达信号数据。实验流程步骤如下：①将数据进行归一化处理；②将预处理后的数据通过聚类算法进行计算；③得到合理的聚类数k和聚类中心；④聚类结果评价。聚类结果如下页表1所示。

通过实验，得到合理的聚类数目为4，与实际给定数据的结果相符合。4类聚类中心信号如下页表2所示。

实验中采用了3种算法进行聚类实验，第1种是k-means算法，第2种是FCM聚类算法，第3种是本文的基于粗糙集改进的k-means算法。引入聚类精度来衡量聚类结果，每种算法取其重复执行10次的平均精度作为最终聚类精度。结果如下页表3所示。可以看出，基于粗糙集改进的k-means算法相比前两种聚类算法具有更高的精度。上述仿真验证了其能够更加有效地对雷达信号进行聚类分选。

4.2基于粗糙集的雷达信号识别仿真分析

基于粗糙集的雷达信号识别仿真主要用于提取出最优规则用于聚类中心信号识别。从已知威胁雷达数据库中提取4类不同用途的雷达，已知样本特征参数如表4所示。

表1 聚类结果

表2 聚类中心信号

表3 聚类精度

根据粗糙集建立知识表达系统，为方便处理作以下标识：序号U，U={u1，u2，…，u10}，载频a，脉冲重复频率b，脉宽c，类别d。对上述数据进行离散化处理，所得结果如表5所示。

由表5可得：

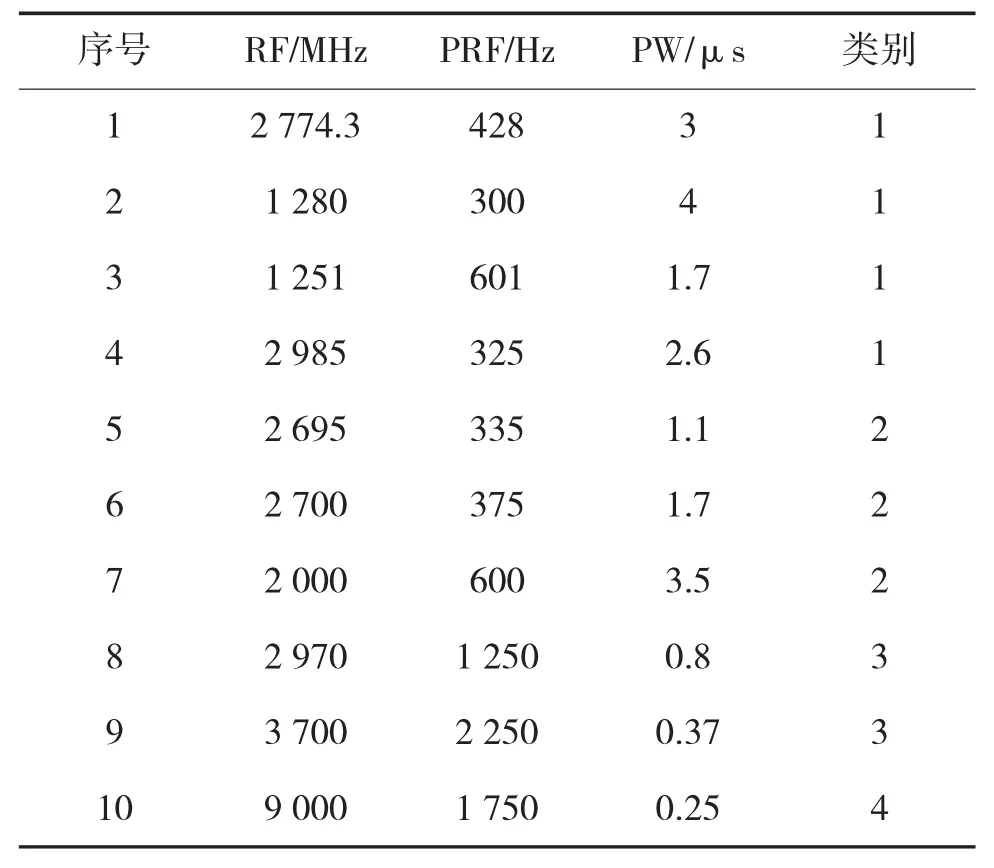
表4 提取的已知威胁雷达数据库实例参数表

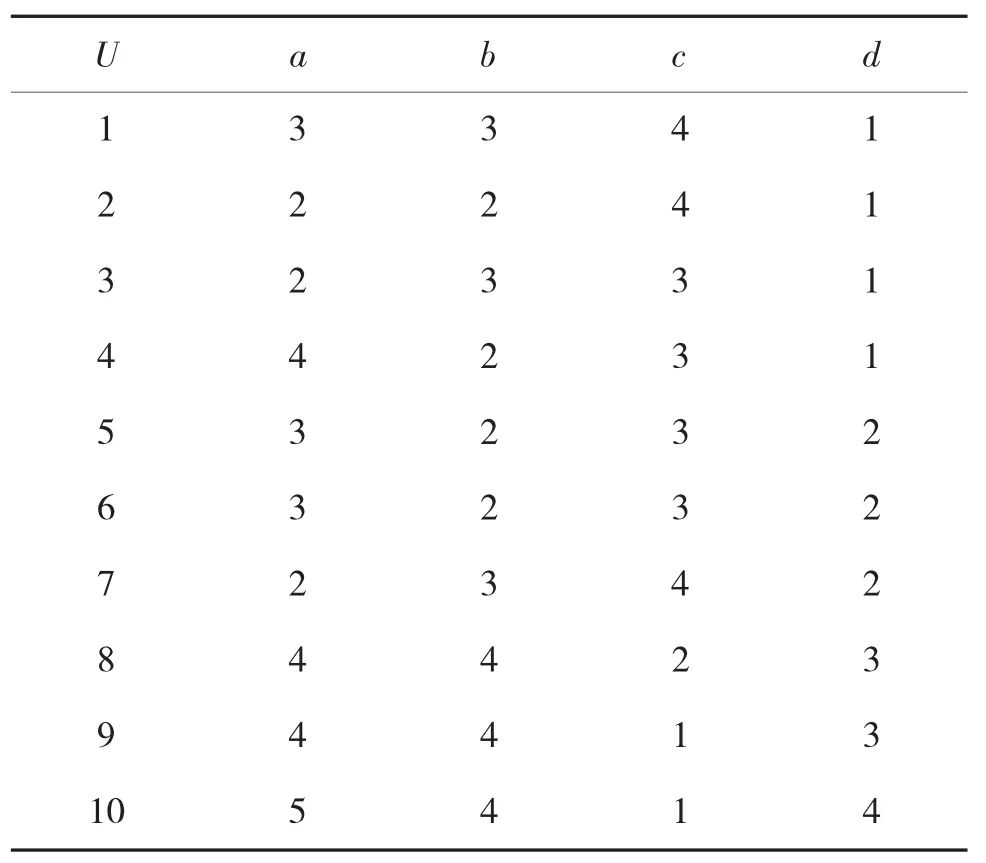
表5 离散后的实例参数表

可见a，b，c属性都是必要的，没有属性可以进行约简，从简化表提取每个对象关于属性值区分的属性，并构成区分函数。

对象1与对象5、6、7、8、9、10关于属性值构成的合取范式为：

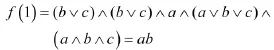
以此类推得包含所有约简决策规则的决策表，并约去所有过剩规则得到包含最优规则集的决策表，如下页表6所示（“*”表示属性值可以省去）。

由表6得到9条规则：第1类识别规则：a3b3→d1、b2c4→d1、b3c3→d1、a4c3→d1；第2类识别规则：a3b2→d2、a2b3c4→d2；第3类识别规则：c2→d3、a4c1→d3；第4类识别规则：a5→d4。

对表2聚类中心信号进行离散化处理，结果如下页表7所示。

采用上述的最优规则进行识别，聚类中心信号1满足a3b3→d1，为第1类；聚类中心信号3满足a3b2→d2，为第2类；聚类中心信号4满足a4c1→d3，为第3类；聚类中心信号2没有相应的识别规则进行识别，无法明确其类别。由上可得，聚类所得第1类～第4类雷达信号为已知威胁雷达数据库中的已知信号，而第2类信号为未知信号，对其需要通过确定其特性后添加到已知威胁雷达数据库。上述仿真验证了基于粗糙集的雷达信号识别能够有效地发现未知雷达信号。

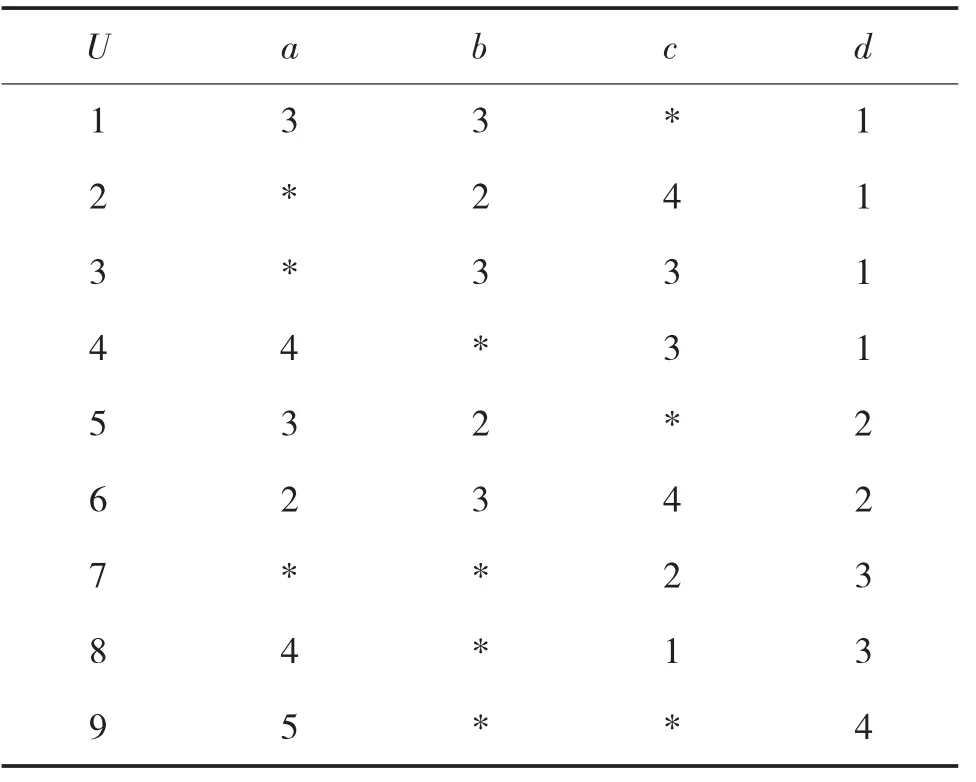
表6 最优规则集

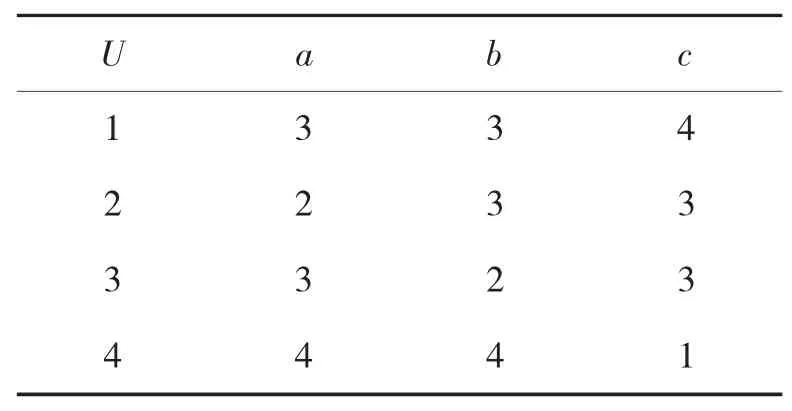
表7 离散化后的聚类中心信号

5 结论

本文提出了一种改进的电子情报分析模型，该模型基于k-means算法和粗糙集分选出记录数据库中的已知信号和未知信号，并将未知信号确定特性后添加到已知威胁雷达数据库中。通过仿真，该模型成功识别出了已知信号和未知信号，验证了其适用性和有效性。

［1］王星.航空电子对抗原理［M］.北京：国防工业出版社，2008.

［2］RICHARD G W.电子情报（ELINT）-雷达信号截获与分析［M］.吕跃广，译.北京：电子工业出版社，2008.

［3］裴云.自卫电子对抗系统对战斗机作战效能的影响分析［J］.电光与控制，2006，13（3）：19-24.

［4］李志伟，仲爱民.机载自卫电子对抗雷达情报分析［J］.现代雷达，2007，29（12）：104-108.

［5］解国良，徐忠伟，王洪迅，等.一种基于相邻脉冲相似性的快速聚类分选方法［J］.火力与指挥控制，2012，37（11），163-165.

［6］张葛祥，金炜东，胡来招.基于粗集理论的雷达辐射源信号识别［J］.西安交通大学学报，2005，39（8）：872-875.

［7］刘旭波，司锡才.基于改进的模糊聚类的雷达信号分选［J］.弹箭与制导学报，2009，29（5）：278-282.

［8］张葛祥，荣海娜，金炜东.支持向量机在雷达辐射源信号识别中的应用［J］.西南交通大学学报，2006，41（1）：25-30.

［9］QIU D X.A comparative study of the k-means algorithm and the normal mixture model for clustering：bivariate homoscedastic case［J］.Journal of Statistical Planning and Inference，2010，140（7）：1707-1711.

［10］陈婷，罗景青.FCM和粗集在雷达信号识别中的应用研究［J］.现代防御技术，2008，36（4）：103-106.

［11］关欣，何友，衣晓.一种新的基于粗集的辐射源信号识别模型［J］.宇航学报，2007，28（3）：685-688.

［12］王佐.基于粗糙集的聚类算法研究［D］.长春：吉林大学，2013.

［13］李楠，曲长文，苏峰，等.基于粗糙集的雷达辐射源信号识别［J］.航天电子对抗，2010，26（4）：8-11.

An Improved Analysis Model of Electronic Intelligence

ZHANG Qiang，WANG Hong-wei，CHEN You，XU Yuan
（School of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi’an 710038，China）

Analysis of electronic intelligence is important to increase the efficiency of ECM.Using a combination of clustering algorithm and sorting algorithm，an improved analysis model of electronic intelligence is established.First，this model completes the clustering of radar signals in record database by using improved k-means algorithm based on rough set，choosing the clustering centers to represent the radar signal clusters.Then，the model uses rough set to extract effective optimal rules to recognize clustering centers pulse recognition，thus to sort the known and unknown signals.Finally，the model ascertains the unknown signals’properties and add them to the known threat database.The simulation validates the model’s feasibility and efficiency.

electronic counter measure，electronic intelligence，k-means algorithm，rough set

TP181

A

1002-0640（2016）11-0124-05

2015-10-17

2015-11-09

陕西省自然科学基金（2012JQ8019）；航空科学基金资助项目（20145596025）

张强（1991-），男，陕西凤翔人，硕士研究生。研究方向：电子对抗理论与技术。