认知MIMO雷达波形设计研究*

兰星，李伟，蒋孟燃，王兴亮，李晓明

（1.空军大连通信士官学校，辽宁大连116600；2.空军工程大学信息与导航学院，西安710077；3.中航雷达与电子设备研究院航空电子系统射频综合仿真实验室，江苏无锡214063）

认知MIMO雷达波形设计研究*

兰星1，2，李伟2，蒋孟燃2，王兴亮2，李晓明3

（1.空军大连通信士官学校，辽宁大连116600；2.空军工程大学信息与导航学院，西安710077；3.中航雷达与电子设备研究院航空电子系统射频综合仿真实验室，江苏无锡214063）

认知多输入多输出（multiple-input multiple-output，MIMO）雷达将认知技术与MIMO技术相结合，具备动态环境信息感知和自适应调节能力，受到雷达界的广泛关注。相比于传统雷达，认知MIMO雷达性能更优、适应性更强，是雷达迈向智能化发展的趋势，而发射波形的优化设计是实现雷达认知的关键，因而成为近年来学者研究的重点。首先介绍了认知MIMO雷达基本概念，分析了波形设计现状，然后在波形设计步骤的基础上，重点从优化准则和优化方法两方面总结了现有研究成果及特点，最后讨论了未来研究方向和需要解决的问题。

认知MIMO雷达，波形优化，优化准则，优化方法

0 引言

认知雷达［1］拥有发射-接收-发射的闭环系统，在与环境不断交互过程中适应环境。Simon Haykin［2］利用仿生知识将认知雷达定义为具有感知周围环境能力的智能、动态的反馈系统。Joseph R.Guerci［3］提出认知雷达应具有环境动态数据库（EDDB）、自适应发射机、知识辅助（KA）处理等先进单元。

多输入多输出技术（MIMO）因采用多天线收发信号而被引入到雷达系统以获取分集增益，有效扩充自由度［4］。天线阵元间距小，通过发射互不相同信号获取分集增益，提升目标识别性能及估计准确度的为集中式MIMO雷达［5］；天线阵元间距大，利用空间分集提升目标检测性能及高分辨率定位能力的为分布式MIMO雷达［6］。认知MIMO雷达将认知与MIMO技术相结合，通过发射机与接收机联合优化设计、自适应多维发射系统信号设计、各种快速有效的知识辅助处理算法，提升雷达在复杂环境中抑制各种干扰、检测和识别目标的性能［7］。认知MIMO雷达结构如图1所示，它具备环境感知能力，发射具有自适应能力的信号，在不断学习调整过程中作出决策使雷达探测目标、参数估计、分辨率等性能最佳。波形设计是凸显雷达认知特征的关键环节，因此，围绕认知MIMO雷达波形设计问题开展研究具有重要意义，是近年来国内外学者关注的焦点。

雷达波形设计分为4个步骤，如图2所示，其中优化准则的确定和优化方法的选取是关键。

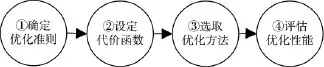
图2 雷达波形设计步骤

1 优化准则

波形优化准则和约束条件由雷达实际场景、工作状态以及任务需求确定，目前主要有如下准则：①以模糊函数为工具，提升雷达信号分辨率、测量精度和杂波抑制能力的波形设计；②旨在以提升信号自相关、降低互相关的完全正交或部分正交波形设计；③基于信息论和统计理论知识，在总发射功率一定等约束条件下研究凸优化问题；④以最大输出信干噪比（Signal-to-Interference plus-Noise，SINR）或信杂噪比（Signal-to-Clutter plus-Noise Ratio，SCNR）为目的，基于环境信息和任务需求，联合优化发射波形和接收滤波器为主的最优波形设计。

1.1基于模糊函数的波形设计

模糊函数最早由J.Ville于1948年提出，在经过P.M.Woodward［8］和A.W.Rihaczek［9］等学者的深入研究后，模糊函数已然成为雷达信号分析和设计的有效工具，它在表征雷达信号固有分辨率和模糊特性的同时，也反映了雷达在距离、速度、测量精度和干扰抑制方面的性能，是近年来雷达界研究的重点。

模糊函数在双基地雷达的应用由T.Tsao［10］等人发展推进。ChunQuan Liu［11］和G.S.Antonio［12］又将模糊函数推广至MIMO雷达，并发现天线数目越多分辨率越高。Chunyang Chen［13］讨论了MIMO雷达模糊函数的一些数学性质，并基于此提出设计正交跳频信号的算法以提高MIMO雷达性能。戴喜增［14］从发射天线结构和信号处理方式两方面寻求频率MIMO雷达距离分辨率提升途径，并从模糊函数角度研究旁瓣类型及抑制方法。秦国栋［15］基于模糊函数研究了稀布阵多载频MIMO雷达分辨率问题，提出新的解速度模糊和发射接收综合处理的方法。

1.2基于相关性的波形设计

因认知MIMO雷达收发端均是多天线结构，为更利于探测识别目标，提升雷达系统性能，MIMO雷达多天线一般采用相互正交的信号，但完全正交信号因实现较难，故在实际雷达系统应用中并不常见，但庆幸的是，部分正交的信号集在一定程度上能满足系统需求，故近年来对于信号相关性的研究也越来越多。JianLi［16］从提高信号自相关、降低互相关角度优化设计信号，提高了雷达分辨率，降低了信号间的相互干扰。胡亮兵［17］研究发现以最小化峰值旁瓣电平设计的正交波形，与最小化相关积分旁瓣电平得到的信号相比，自相关峰值旁瓣电平和峰值互相关电平都要更低。申东［18］利用混沌序列降低MIMO雷达波形自相关旁瓣和互相关，通过多脉冲压缩积累能有效改善MIMO雷达性能。XiufengSong［19］通过空时编码技术来减弱MIMO雷达中波形互相关影响。

1.3基于信息论和统计理论的波形设计

将信息论知识应用于雷达系统设计最早可追溯到1951年，Woodward［20］应用信息论设计雷达接收机，而将信息论用于雷达波形设计则始于1993年Bell［21］将最大化目标脉冲响应和目标回波间互信息量（MI）作为雷达波形优化准则应用于扩展目标估计，并发现互信息量的高低将影响到雷达在目标检测和参数估计方面的性能。

此后，诸多研究者基于互信息量对波形优化设计进行研究。A De Maio［22］基于MI优化时空编码信号，并验证目标的恒虚警检测性能；A.Leshem［23］基于MI优化多目标环境的雷达波形；Y.Yang［24-25］分别从最大化目标响应和目标回波间MI和统计意义上的最小化目标响应均方误差角度优化设计信号，发现目标特性已知时，两者估计性能一致，目标特性未知时性能并不一致；纠博［26］针对杂波环境提出优化设计雷达波形的通用注水法，并应用于改善目标识别性能，在频域基于MI优化设计雷达波形；赵瑞丽［27］分别从最大MI和最小均方误差（MMSE）矩阵的迹优化分布式MIMO雷达波形，并分析自由度、杂波相关系数和信号编码长度等对目标检测性能的影响；Wenshu Zhang［28］在色噪声统计特性未知和多目标环境下，分别基于MI、MMSE及最小化归一化均方误差（NMSE）优化波形，发现三者性能均不一致，且后两者性能更接近；唐波［29］分别从最大化MI和最大化相对熵的角度进行波形优化设计；李树峰［30］和S.Sen［31］基于MI分别针对完全互补序列和正交频分复用信号调制波形进行优化，分别用于提高信道容量和实现目标跟踪；T.Naghibi［32］针对杂波环境分别基于MI和MMSE优化雷达波形；R. A.Romero［33］分别从最大化信噪比（SNR）和最大化MI角度优化设计杂波背景中雷达波形，并找到两准则间的关联；Xiufeng Song［34］根据在电子战环境中雷达和目标察觉对方与否，以MI为准则基于博弈论知识提出雷达信号与目标干扰博弈过程中的两步注水优化；Yifu Chen［35］提出先最大化目标脉冲响应和目标回波间MI，后最小化连续散射回波信号间MI的两步优化算法；崔海静［36］基于MI准则对雷达波形的极化方式进行优化，获得了较好的效果。

需提出的是，基于互信息量优化设计雷达波形是在目标、杂波及噪声等统计特性已知或部分已知情况下进行的，这依赖于雷达认知功能的发挥，能否获取目标先验知识以及先验知识数量将决定该准则是否适用于相应雷达调度需求范围，而诸如MMSE，NNSE等方法同样也是基于统计理论开展研究的，而统计理论正好与雷达在目标检测与参数估计方面性能的应用相契合，具有研究的价值与意义。

1.4基于SINR或SCNR的波形设计

认知MIMO雷达接收端的输出信干噪比（SINR），反映了雷达在目标检测、参数估计等方面的能力。B.Friedlander［37］基于训练数据以最大化输出SINR为优化准则设计适应波形，C.Y.Chen［38］同样最大化SINR，但所用算法为循环优化发射波形与接收滤波器，这样能保证每次循环迭代SINR非降，在此基础上，Guolong Cui［39］研究受恒模和相似性限制的波形设计，提出两种连续优化算法最大化SINR。Shuangling Wang［40］基于已感知的目标、杂波以及噪声的统计特性，假使各天线发射线性调频信号可具有不同起始频率和带宽，受工作频率允许范围及发射总能量的限制通过迭代算法最大化接收机输出信杂噪比（SCNR）。Yonghao Tang［41］将发射波形与接收滤波联合迭代优化的算法应用到空频MIMO雷达中最大化SCNR，并通过注水法分配各载频通道能量。

2 优化方法

波形设计在确定优化准则和代价函数时，优化方法的选取则是影响波形性能优劣的主要因素，归纳起来，针对最优波形求解的方法主要包含特征值法、注水定理和现代智能优化算法3类。

2.1特征值法

通过特征值法求解的最优波形一般为某最大特征值对应的特征向量［42］，基于环境先验信息应用特征值法得到的优化波形能够增强雷达认知自适应能力，提升雷达系统性能。

目标脉冲响应已知时，J.R.Guerci［43］以最大化异类目标回波间差异来优化发射波形。D.A.Garren［44］在不确定目标方位时，通过最大化异类目标各方位回波间马氏距离平方的平均值优化波形。Yimin Wei［45］在2009年的IET国际雷达会议上提出了基于特征值法的序列波形优化方法。

2.2注水定理

MIMO通信中，为使信道容量最大，需使信噪比大的信道分得的功率多，信噪比小的信道分得的功率少，此即注水定理。类似于MIMO通信，认知MIMO雷达同样需要根据其信号传输途径及环境状况自适应分配信号功率，即应用注水定理优化发射波形以使雷达系统性能最佳。

应用注水定理优化噪声环境中雷达波形最早由Bell［21］提出，A.Leshem［30］将其应用于多目标环境下的雷达波形优化，此后A De Maio［22］，Yang Yang［24-25］，Wenshu Zhang［27］，Bo Tang［29］等针对噪声环境的雷达波形优化深入研究，纠博［26］提出杂波和噪声环境的通用注水法是注水定理的推广，Xiufeng Song［34］针对雷达与目标施放的干扰间的博弈，提出了两步注水的方法。

2.3现代智能优化算法

实际电子战环境中，雷达往往面临较为复杂的局势和作战任务需求，设定的代价函数也相对较复杂，非线性约束条件居多，非凸优化情况更常见，所以常规优化方法难以满足既定需求，此时就需要采用有效的现代智能优化算法来优化波形。现代智能优化算法主要有：模拟退火算法、禁忌搜索、遗传算法、粒子群算法等，以及多种算法结合的混合算法。

Hai Deng提出基于模拟退火算法优化设计正交多相码［46］；刘波基于遗传算法或改进的遗传算法针对频率正交线性调频信号（OFD-LFM）［47］和离散频率编码［48］波形进行研究，丰富了MIMO雷达信号形式；李敬军［49］提出适用于宽带MIMO雷达的DFCW波形设计的改进离散粒子群算法，并简化设置代价函数得到新编码信号。王伟［50］把完整的禁忌搜索算法引入并作为遗传算法的变异算子以优化MIMO雷达正交多相码波形，结合了遗传算法全局搜索和禁忌搜索算法局部搜索能力，优化能力更强，有效降低了发射信号的自相关旁瓣和互相关。

3 讨论与展望

（1）现有波形研究主要针对高斯杂波、噪声环境为主，而实际中杂波及噪声分布较复杂，尤其是系统分辨率满足要求时，杂波和噪声一般需考虑非高斯分布的模型。建立针对不同环境的雷达波形数据库，对认知MIMO雷达实时选择最优波形探测识别目标意义重大；

（2）雷达与目标始终处于复杂的电子战环境，双方进行着非生即死的零和博弈，在认知MIMO雷达波形设计时，应将来自目标方干扰机施放的干扰考虑在内，如何基于先验知识，在波形设计阶段就使雷达波形具有良好的抗干扰性能将是今后研究的重点；

（3）认知MIMO雷达优化波形性能上的优劣很大程度上依赖于先验知识获取途径，随着时代的进步，先验知识的获取技术也正蓬勃发展，在既考虑资金成本、设备复杂度的基础上，又提高先验知识的获取效率有着深远意义；

（4）现有波形设计准则在优化雷达波形提升雷达某一性能时，会导致其他方面性能的下降，因此，有必要联合多准则优化设计认知MIMO雷达波形，在提高目标检测识别定位、参数估计、抗干扰抗截获等方面提出一个综合方案，在实现雷达智能化的同时实现多功能化。

［1］HAYKIN S.Cognitive radar networks［C］//2005 1st IEEE International Workshop on Computational Advances in Multi-SensorAdaptiveProcessing，PuertoVallarta，Mexico，2005：1-3.

［2］HAYKIN S.Cognitive radar：a way of the future［J］.IEEE Signal Processing Magazine，2006，23（1）：30-40.

［3］GUERCI J R，BARANOSKI E J.Knowledge-aided adaptive radar at DARPA［J］.IEEE Signal Processing Magazine，2006，23：41-50.

［4］陈浩文，黎湘，庄钊文.一种新兴的雷达体制———MIMO雷达［J］.电子学报，2012，40（6）：1190-1198.

［5］HASSANIEN A，VOROBYOV S A.Subspace-based direction finding using transmit energy focusing in MIMO radar with colocated antennas［C］//IEEE International Conference on Acoustics Speech and Signal Processing（ICASSP），2011：2788-2791.

［6］DIANAT M，TABAN M R，DIANAT J，et al.Target localization using least squares estimation for MIMO radars with widely separated antennas［J］.IEEE Transactions on AerospaceandElectronicSystems，2013，49（4）：2730-2741.

［7］GUERCI J R.Cognitive radar：a knowledge-aided fully adaptive approach［C］//IEEE Radar Conference，2010.

［8］WOODWARD P M.Probability and information theory，with applications to radar［M］.Norwood，MA：Artech House，1953.

［9］RIHACZEK A W.Principle of high-resolution radar［M］.Los Altos：Peninsula Publishing，1985.

［10］TSAO T，WEINER D，VARSHNEY P，et al.Ambiguity function for a bistatic radar［J］.IEEE Transactions on AerospaceandElectronicSystems，1997，33（3）：1041-1051.

［11］LIU C，ZHANG J，QU J.The ambiguity function of MIMO radar［C］//IEEE International Symposium on Microwave，Antenna，Propagation，and EMC Technologies For Wireless Communications，2007：265-268.

［12］ANTONIO G S，FUHRMANN D R，ROBEY F C.MIMO radar ambiguity functions［J］.IEEE Selected Topics in Signal Processing，2007，1（1）：167-177.

［13］CHEN C Y，VAIDYANATHAN P P.MIMO radar ambiguity properties and optimization using frequency-hopping waveforms［J］.IEEE Transactions on Signal Process，2008，56（12）：5926-5936.

［14］DAI X，XU J，PENG Y.High resolution frequency MIMO radar［C］//Proceedings of the IEEE Conference on Radar，Waltham，MA，USA，2007：693-697.

［15］秦国栋，陈伯孝，陈多芳，等.多载频MIMO雷达解速度模糊及综合处理方法［J］.电子与信息学报，2009，34（4）：794-797.

［16］LI J，STOICA P.MIMO radar signal processing［M］.New York：John Wiley&Sons，2009.

［17］胡亮兵，刘宏伟，吴顺君.基于约束非线性规划的MIMO雷达正交波形设计［J］.系统工程与电子技术，2011，33（1）：64-68.

［18］申东，张林让，刘昕，等.用混沌序列降低MIMO雷达波形自相关旁瓣和互相关［J］.西安电子科技大学学报，2012，39（5）：42-46，60.

［19］SONG X，ZHOU S，WILLETT P.Reducing the waveform cross-correlation of MIMO radar with space time coding［J］. IEEE Transactions on Signal Processing，2010，58（8）：4213-4224.

［20］WOODWARD P M.Information theory and the design of radar receivers［J］.Proc IRE，1951，1（1）：1521-1524.

［21］BELL M R.Information theory and radar waveform design［J］.IEEE Trans Inform Theory，1993，39（5）：1578-1597.

［22］MAIO A D，LOPS M.Design principles of MIMO radar detectors［J］.IEEE Transactions on Aerospace and Electronic System，2007，43（3）：886-898.

［23］LESHEM A，NAPARSTEK O，NEHORAI A.Information theoretic adaptive radar waveform design for multiple extended targets［J］.IEEE Journal on Selected Topics in Signal Processing，2007，1（1）：42-55.

［24］YANG Y，BLUM R S.Minimax robust MIMO radar waveform design［J］.IEEE Journal on Selected Topics in Signal Processing，2007，1（1）：147-155.

［25］YANG Y，BLUM R S.MIMO radar waveform design based on mutual information and minimum mean-square error estimation［J］.IEEE Transactions on Aerospace and Electronic System，2007，43（1）：330-343.

［26］纠博，刘宏伟，李丽亚，等.一种基于互信息的波形优化设计方法［J］.西安电子科技大学学报，2008，35（4）：678-684.

［27］赵瑞丽.MIMO雷达发射波形优化设计［D］.西安：西安电子科技大学，2009.

［28］ZHANG W，YANG L.Communications-inspired sensing：a case study on waveform design［J］.IEEE Transactions on Signal Processing，2010，58（2）：792-803.

［29］TANG B，TANG J，PENG Y.MIMO radar waveform design in colored noise based on information theory［J］.IEEE TransactionsonSignalProcessing，2010，58（9）：4684-4697.

［30］LI S F，CHEN J，ZHANG L Q.Optimisation of complete complementary codes in MIMO radar system［J］.Electronics Letters，2010，46（16）：49-53.

［31］SEN S，NEHORAI A.OFDM MIMO radar with mutual-information waveform design for low-grazing angle tracking［J］.IEEE Transactions on Signal Processing，2010，58（6）：3152-3162.

［32］NAGHIHI T，NAMVAR M，BEHINA F.Optimal and robust waveform design for MIMO radars in the presence of clutter［J］.IEEE Transactions on Signal Processing，2010，90（4）：1103-1117.

［33］ROMERO R A，JUNHYEONG B，GOODMAN N A.Theory and application of SNR and mutual information matched illumination waveforms［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47（2）：912-927.

［34］SONG X，WILLETT P，ZHOU S，et al.The MIMO radar and jammer games［J］.IEEE Transactions on Signal Processing，2012，60（2）：687-699.

［35］CHEN Y，NIJSURE Y，YUEN C，et al.Adaptive distributed MIMO radar waveform optimization based on mutual information［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（2）：1374-1385.

［36］崔海静.分布式MIMO雷达极化波形设计方法研究［D］.长春：吉林大学，2014.

［37］FRIEDLANDER B.On data-adaptive waveform design for MIMO radar［C］//in Proc.41th Asilomar Conf.Signals，Syst.，Comput.（ACSSC），Pacific Grove，CA，USA，2007：187-191.

［38］CHEN C Y，VAIDYANATHAN P P.MIMO radar waveform optimization with prior information of the extended target and clutter［J］.IEEE Transactions on Signal Processing，2009，57（9）：3533-3544.

［39］CUI G，LI H，RANGASWAMY M.MIMO radar waveform design with constant modulus and similarity constraints［J］. IEEE Transactions on Signal Processing，2014，62（2）：343-353.

［40］WANG S，HE Q，HE Z.LFM-based waveform design for cognitive MIMO radar with constrained bandwidth［J］. EURASIP Journal on Advances in Signal Processing，2014：89：1-9.

［41］TANG Y，MA X，SHENG W，et al.Transmit waveform optimization for spatial-frequency diversity MIMO radar in the presence of clutter［J］.International Journal of Antennas and Propagation，2014（10）：1-9.

［42］黎湘，范梅梅.认知雷达及其关键技术研究进展［J］.电子学报，2012，40（9）：1863-1870.

［43］PILLAI S U，GUERCI J R，PILLAI S R.Joint optimal tx-rx design for multiple target identification problem［C］//Sensor Array and Multichannel Signal Processing Workshop Proceedings 2002：553-556.

［44］GARREN D A，OSBORN M K，ODOM A C，et al.Optimal transmission pulse shape for detection and identification with uncertain target aspect［C］//Proceedings of the IEEE Radar conference 2001，Atlanta，GA，2001：123-128.

［45］WEI Y，MENG H，WANG X.Adaptive single-tone waveform design for target recognition in cognitive RADAR［C］// IET Radar International Conference 2009，Guilin，China，2009.

［46］DENG H.Polyphase code design for orthogonal netted radar systems［J］.IEEE Trans on Signal Processing，2004，52（11）：3126-3135.

［47］刘波，韩春林，苗江宏.MIMO雷达正交频分LFM信号设计及性能分析［J］.电子科技大学学报，2009，38（1）：28-31.

［48］LIU B，HE Z，HE Q.Optimization of orthogonal discrete frequency-coding waveform based on modified genetic algorithm for M IMO radar［C］//International Conference on Communications，Circuits and Systems（ICCCAS），2007：966-970.

［49］李敬军，姜永华，但波.MIMO雷达中正交离散频率编码波形的设计［J］.信号处理，2013，29（9）：1176-1181.

［50］王伟，赵俊杰，王辉.基于混合算法的MIMO雷达正交多相码设计［J］.系统工程与电子技术，2013，35（2）：294-298.

Overview on Waveform Design of Cognitive MIMO Radar

LAN Xing1，2，LI Wei2，JIANG Meng-ran2，WANG Xing-liang2，LI Xiao-ming3
（1.Dalian Airforce Communication NCO Academy，Dalian 116600，China；
2.School of Information and Navigation，Air Force Engineering University，Xi’an 710077，China；
3.Aviation Key Lab.of Science and Technology on AISSS，The Institute of Radar and Electronic Equipment，Wuxi 214063，China）

Cognitive multiple-input multiple-output（MIMO）radar is a combination of cognitive technology and MIMO technology，it has the perceptive ability of dynamic environment information and the adaptive ability to adjust the waveform，which has been attracting much attention of researchers in the field of radar.Compared with traditional radar，cognitive MIMO radar has better performance and stronger adaptability，thus it is the trend of radar which develops toward the direction of intelligence. The technique of waveform design is the key to help radar realize cognitive function，so it has obtained much attention and been intensively studied in recent years.In this paper，basic concept of cognitive MIMO radar is introduced and current situation of waveform design is analyzed firstly，then based on the steps of waveform design，existing research results mainly from the perspective of optimization criterion and optimization method are summarized，finally future research directions and problems need to be solved are discussed and prospected.

cognitive MIMO radar，waveform design，optimization criterion，optimization method

TN957

A

1002-0640（2016）11-0001-05

2015-10-05

2015-11-07

国家自然科学基金（61302153）；航空基金（20140196003）；航天科技创新基金资助项目（CASC020302）

兰星（1991-），男，湖南岳阳人，硕士，研究方向：MIMO雷达信号优化设计。