授之以鱼，不如授之以渔

翁爱兰

摘 要：“现代技术的使用将会深刻影响数学教学内容、方法和目标的改变”。随着近几年微课的发展，课堂早已不是“三尺讲台+一块黑板+一支粉笔”，如今课堂有更丰富的内容、形式。几何概型是高一学生学完概率的古典概型后的又一概率模型，是对古典概型内容的进一步拓展，是等可能事件的概念从有限向无限的延伸，借助微课通过类比、启发、猜想、探究得到几何概型的定义、计算公式。作者借助最近研究的微课课题写了教学随笔。

关键词： 几何槪型 无限 等可能 事件

一、教学目标

二、教学分析

三、教学过程设计

（一）新课引入：观看微课视频。

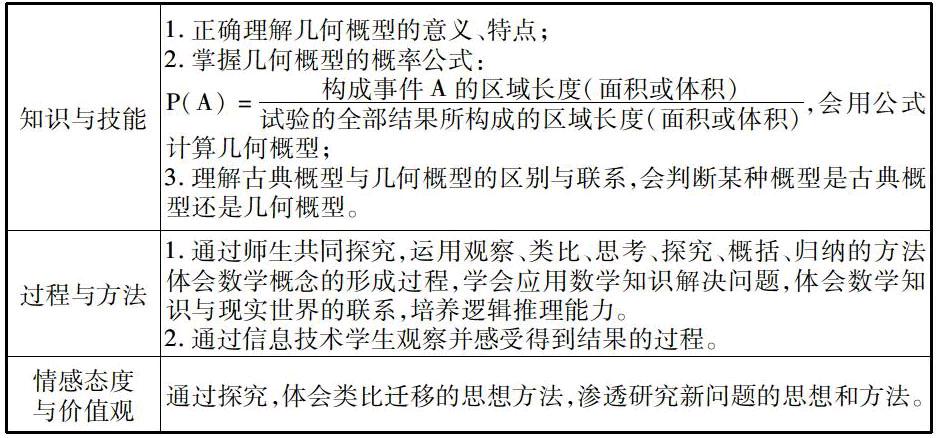
1.学生观看微课视频3分钟，主要内容：甲、乙两人玩转盘游戏。旋转转盘，当转盘停止时，指针可以指向转盘上的任意位置。规定当转盘停止时指针指向B区域，乙胜；否则甲胜。求乙胜的概率。（转盘被六等分）

同学A：0.5，因为总的基本事件有6个，每个基本事件发生的概率都是等可能的，又因为B区域有3个，当指针指向B时乙胜，这是古典概型，所以乙胜的概率为0.5。

同学B：不对，这题不是古典概型。我认为应该用圆弧比表示概率，答案是0.5。

同学B：我认为不是古典概型，但也不同意B的做法，我是用面积比表示所求概率，答案也是0.5。

老师：这个问题中的基本事件是什么？

学生：基本事件是转盘停止时指针的位置。

老师：基本事件个数怎样？

学生：它有无限个。

老师：基本事件等可能吗？

学生：等可能。

老师：如何求解？

[设计意图]通过观看微课视频，引起学生认知上的冲突，进而引出新的思考、新的问题。

2.学生观看微课视频2分钟，主要内容：古典概型的定义、特点、公式。

老师：古典概型中，事件A的概率只要数清A所含的基本事件的个数与全部基本事件的个数，它们的比值就是这个事件的概率。上面的问题还能用个数比求事件的概率吗？基本事件能数得出来吗？

学生：不能。

老师：类比古典概型的特点及其概率公式，能否找到一个合适的方法研究上面的问题。

[设计意图]通过观看微课视频，复习旧知，起到承上启下的作用。

（二）类比启发：数学的眼光观察。

学生思考2分钟，小组讨论交流。

学生：全部基本事件构造成一个圆，把“乙胜”这个事件的基本事件构造成3个扇形，然后用它们的面积之比求概率，答案应该是0.5。

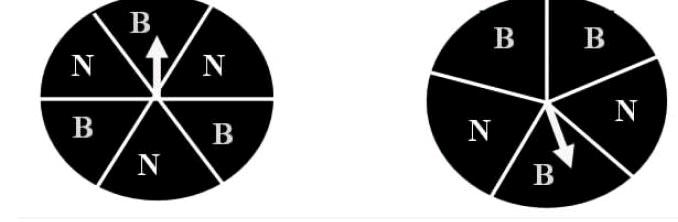
老师：很好，请坐。还是古典概型的思想，不同的是我们构造成了扇形与圆。利用它们的面积之比求概率。若把圆B区域移动，如右图，乙胜的概率是多少？

学生：还是0.5。

老师：如果改为正方形呢？

学生：0.5。

老师：以上现象说明什么？有什么共同特点？

学生：“乙胜”的概率与B区域的位置无关；只与B区域的面积所占的比例有关。

老师：很好。我们的想法是：虽然基本事件的个数为无限个，无法一一数出来。但我们可以把事件A的基本事件和全部基本事件分别构造成两个可以度量的几何图形。然后用它们的几何度量之比求概率。

思考1：有一根长度为3m的绳子，拉直后在任意位置剪断，那么事件A：剪得的两段的长度都不小于1m的概率是多少？你是怎样计算的？（利用幻灯片展示）

老师：这个问题中的基本事件是什么？

学生：剪刀可以剪到的任意位置。

老师：个数怎样？是不是等可能的？

学生：无限个，等可能。

老师：如何求解？

学生：我觉得可以把全部基本事件构造成长度为3m的绳子的这条线段，把事件A的基本事件构造成这条线段上从1m到2m之间的线段，那么事件A的概率就可以用这两条线段的长度之比计算。结果应该是。

老师：很好。我们的想法是虽然基本事件的个数为无限个，无法一一数清。但我们可以把事件A的基本事件和全部基本事件分别构造成两个可以度量的几何图形。然后用它们的几何度量之比求概率。

[设计意图]抽象出几何概型的另一种几何度量——长度。

思考2：一只海豚在一个长40m，宽30m，深20m的水池中自由游弋，求它距离池底与池壁均不小于5m的概率。（利用幻灯片展示）

老师：这个问题中的基本事件是什么？

学生：海豚在水池中的位置。

老师：个数怎样？是不是等可能的？

学生：无限个，等可能。

老师：如何求解？

学生：把海豚任意位置抽象为一个点，这样全部基本事件可构造成一个长为40m，宽为30m，高为20m的长方体。而把事件A的基本事件构造成一个长为30m，宽为20m，高为15m的长方体。用它们的体积之比求概率。

老师：思想一样，这里构造成了立体图形，用体积之比求概率。

[设计意图]抽象出几何概型的另一种几何度量——体积。

通过以上三个例子的研究发现它们的共同点：

（1）基本事件的个数是无限的；（2）每个基本事件发生的可能性相等；（3）都可用几何图形的几何测度求概率。

具有以上特点的概率模型就是我们今天要研究的主要内容。因为这种概率模型需要借助几何图形求解，所以我们称之为“几何概型”。

[设计意图]从数学学科这个整体来看，数学的高度抽象性造就了数学的难懂、难学，解决这一问题的基本途径是顺应学习者的认知规律，在可能情况下尽量做到从直观入手，从具体开始，逐步抽象。通过师生互动探究，使概念的生成自然，容易被接受。

（三）探究归纳：明确基本概念。

几何概型的概念：

（1）无限性：基本事件的个数都是无限个；

（2）等可能：每个基本事件发生的可能性都相等；

（3）成比例：每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例。

古典概型和几何概型之间有怎样的区别与联系呢？

学生：它们的共同之处在于：①等可能性；②公式都是比的形式。

它们的不同点在于：古典概型中基本事件的个数是有限个；而几何概型中基本事件的个数是无限个。

老师：学习几何概型之后，我们判断以下概率问题属于哪种概率模型？（利用幻灯片展示）

判断下列概率问题的基本事件是什么，属于哪种概率模型

1.抛掷两颗骰子，求出现两个“6点”的概率。

2.两根相距6m的木杆上系一根绳子，并在绳子上挂一盏灯，求灯与两端距离都大于2m的概率。

老师：今后当我们遇到概率问题时，首先要像这样判断这属于哪种概率模型，然后用相应概率公式求解。请看一道例题：（利用幻灯片展示）

（四）应用举例：巩固基本概念。

例1：某人午觉醒来，发现表停了，他打开收音机，想听电台整点报时，求他等待的时间不多于10分钟的概率。

学生思考、讨论，教师适当引导。

[设计意图]心理学认为：概念一旦形成，就必须及时加以巩固，通过例1加深学生对几何概型理解及公式的应用。

（五）归纳总结：加深基本概念。

老师：通过本堂课学习你收获了什么？

学生：1.几何概型及特点，计算公式。2.研究概率时，先研究是古典概型还是几何概型。接下来利用概率公式求解。

[设计意图]知识性内容的总结，可以把课堂教学传授的知识尽快转化为学生的素质。

四、课后反思

（一）良好的开篇是成功的一半。

本课是一节概念课，如何循序渐进地引入新课，由易到难地提出问题，使概念生成水到渠成，刚开始借助的微课视频主要目的是：引导学生来到教师预设的方向，使学生关注这个问题与古典概型的区别，进而引发认识上的冲突。由于本节引入精彩独特，让学生在感兴趣的人物对话情境中进入本节学习，从而激发了学生的学习兴趣。

（二）授之以鱼，不如授之以渔。

笔者曾思考了多种方式教学，最终以“教是为了不教”，“授之以鱼，不如授之以渔”为主导思想，课堂上以教师为主导，学生为主体，发挥学生主观能动性，以多种相似问题情境研究相同问题，根据已有古典概型的知识类比、猜想、归纳总结、得到概念等教学过程。由于前面做了较多铺垫，得到几何概型概念后学生自然得到了几何概型的计算公式，并进行了几何概型与古典概型的区别联系。学习知识的同时，又培养了主动学习能力，如何学，怎么学。我想通过本节学习学生一定会印象深刻。

参考文献：

[1]耿熹.几何概型“等可能性”的教学思考.福建省第三届基础教育优秀论文汇编.

[2]李青林，刘运新.注重概念形成过程，彰显课堂灵魂魅力——微课“离散型随机变量的均值与方差的定义”的教学随笔[J].数学通讯（下半月），2016（1）：15-17.

本文系2014年度福州市教育信息技术研究立项课题“基于微课的高中数学教学研究”（编号：FZDJ2014B10）的阶段研究成果。