基于核距离的直觉模糊c均值聚类算法
2016-12-08余晓东雷英杰宋亚飞岳韶华申晓勇
余晓东,雷英杰,宋亚飞,岳韶华,申晓勇
(空军工程大学防空反导学院,陕西西安 710051)
基于核距离的直觉模糊c均值聚类算法
余晓东,雷英杰,宋亚飞,岳韶华,申晓勇
(空军工程大学防空反导学院,陕西西安 710051)
针对现有直觉模糊c均值聚类算法无法发现非凸聚类结构的缺陷,提出了一种基于核化距离的直觉模糊c均值聚类算法.算法在定义了基于核的直觉模糊欧式距离基础上,通过把聚类样本映射到高维特征空间,使原来没有显现的特征突现出来,从而能够更好地聚类.实验选择一组人工数据集及一组UCI数据集测试了本文算法,并将其与五种经典的聚类算法进行了比较.实验结果充分表明了该算法的有效性及优越性.
直觉模糊集;直觉模糊聚类;核方法;无监督学习
1 引言
著名学者Ruspini[1]首先提出模糊划分的概念,将Zadeh模糊集理论引入到聚类分析中来.随后,研究者们提出了多种模糊聚类分析方法,主要包括基于模糊等价关系的传递闭包方法、基于相似性关系和模糊关系的方法以及基于模糊图论的最大树方法等,但是这些方法计算复杂度高,难以应用于大数据问题及实时性要求较高的领域,因而在实际应用与研究中已逐步减少[2].模糊c均值算法[3](Fuzzyc-Means,FCM)是一种基于目标函数的聚类方法,它能够通过优化目标函数得到各样本相对各聚类中心的隶属度,从而达到自动分类的目的,而广泛应用于模式识别、信息融合、网络安全、图像处理等领域.随着Zadeh模糊集以及模糊聚类方法的日趋成熟,其隶属度单一的局限性也逐渐显现[4].直觉模糊集(Intuitionistic Fuzzy Sets,IFS)作为Zadeh模糊理论最重要的拓展形式之一,因其增加了犹豫度属性参数,从而进一步扩展和增强了模糊集理论对复杂不确定性知识的描述与处理功能,为模糊不确定性信息的建模与处理提供了新的思路和方法[5,6].文献[7]将聚类对象及聚类中心点用直觉模糊集表示,提出来基于直觉模糊集合的模糊c均值(Intuitionistic Fuzzyc-means Clustering,IFCM)算法.目前,IFCM算法虽然取得了一些较好的应用效果,但同样也继承了经典FCM算法的一些缺点,如对噪声和野值敏感,并且过于依赖样本数据的分布结构,对复杂的数据结构显得无能为力.
针对这个问题,核方法被引入到此类算法中来.1995年,Cortes和Vapnik[8]提出了支持向量机(Support Vector Machine,SVM)理论,SVM在很多领域都体现出比传统分类器更好的性能,使得核方法逐渐受到重视并被应用到机器学习领域的各个方面[9,10].Girolami[11]创造性地提出了模糊核c均值算法(Fuzzy Kenelc-Means,FKCM)算法,解决FCM算法不能发现非凸聚类结构的问题.文献[12]提出了一种直觉模糊核聚类算法(Intuitionistic Fuzzy Kernel c-means Clustering Algorithm,IFKCM),但该方法为方便计算令样本相对各类别隶属度之和为1,与直觉模糊思想不符.文献[13]通过提取核空间的几何特性,提出了一种自适应确定聚类数的核聚类方法.文献[14,15]在经典FCM算法中引入折中权重模糊因子和核距离度量,提出了一种基于模糊因子的核聚类算法,并将其应用于图像分割领域.鉴于此,本文尝试将核方法与直觉模糊聚类方法理论相结合,并给出一种基于核化距离的直觉模糊c均值聚类算法(Kernel-based Intuitionistic Fuzzyc-means Clustering Algorithm,K-IFCM).
2 基于核的直觉模糊距离度量
定义1(直觉模糊欧式距离度量[5]) 若样本x=(x1,x2,…,xn)和样本y=(y1,y2,…,yn)均可用直觉模糊集表示,则它们之间的直觉模糊欧式距离可定义如下:
(1)
目前,绝大多数直觉模糊聚类算法均使用模式空间的直觉模糊欧式距离作为距离测度,然而现实中大多数聚类问题往往具备了直觉模糊欧式距离无法反映的复杂结构.图1给出了一个简单的示例,图中的数据为人工同心圆样本数据,采用直觉模糊欧式距离测度后的聚类效果如图1所示.可以看出,基于直觉模糊欧式距离,具有复杂数据结构的聚类样本在低维模式空间线性不可分.

基于以上分析,我们尝试将样本间的直觉模糊欧式距离投影到特征空间,并基于核方法
‖Φ(x)-Φ(y)‖2=K(x,y)-2K(x,y)+K(x,y)
(2)
给出基于核的直觉模糊欧式距离.
定义2(基于核的直觉模糊欧式距离度量) 若样本x=(x1,x2,…,xn)和样本y=(y1,y2,…,yn)均可用直觉模糊集表示,则它们之间基于核的直觉模糊欧式距离可定义如下:
(3)
3 基于核的直觉模糊c均值聚类算法
3.1 公式推导
设X={x1,x2,…,xn}⊂Rs为模式空间内的一组有限观测样本集,假定每个样本的特征均为s维的直觉模糊集,可表示为xi={
样本xi与聚类中心pi之间的关系为模糊关系,对样本X的分类结果仍然是一个模糊矩阵U=(μij)c×n,且满足条件:
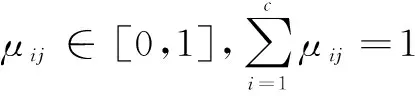
通过求出适当的直觉模糊分类矩阵U和聚类中心P,使目标函数
(4)
最小,其中m称作平滑参数,‖Φ(xi)-Φ(pi)‖2为样本xi与聚类中心pi之间核距离,本文在这里采用定义2给出的基于核的直觉模糊欧式距离度量,将式(3)带入式(4)得目标函数为:
(5)
注意到式(5)并没有选择特定的核函数,因此任何满足Mercer条件[9]的核函数K(x,y)都可适用该式.下面是两个常用的Mercer核函数:
高斯核函数:KG(x,y)=exp(-‖x-y‖2/σ2),σ为自定义的参数.
多项式核:KD(x,y)=(x·y+b)d,b,d为自定义的整数参数.
由于高斯核函数对应的是无穷维的特征空间,而有限样本数据在无穷维特征空间一定线性可分的,因此,在实际应用中通常采取高斯核函数.而对于高斯核函数,有∀x∈X,KG(x,x)=1,因此基于高斯核的直觉模糊欧式距离可以简化为
(6)
这是一个关于自变量(U,P)的约束优化问题,由拉格朗日乘数法可得目标函数为:
(7)
其中,λ为拉格朗日乘数.由极值点的KT必要条件可得:
(8)
(9)
·(-2(xμj-pμj)))=0
(10)
·(-2(xμj-pμj)))=0
(11)
若∀i,i=1,2,…c,使得DK-IFE(xj,pi)>0,则
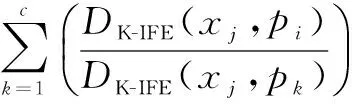
(12)
若∀i,i=1,2,…c,使得DK-IFE(xj,pi)=0,则
(13)
同理,可得聚类中心的迭代公式为:
(14)
(15)
3.2 算法步骤
下面给出基于核化距离的直觉模糊c均值聚类算法的详细步骤:
算法1 基于核化距离的直觉模糊c均值聚类算法
输入:样本数据集X,聚类类别数c,平滑参数m,核函数及其参数,最大迭代次数k,迭代停止阈值η.
输出:划分隶属矩阵U,聚类中心P,迭代次数k.
Step1:初始化聚类中心P,令迭代次数t=1;
Step2:根据式(12)、(13)计算划分隶属矩阵U;
Step3:根据式(14)、(15)计算新的聚类中心点;
Step4:判断是否满足终止条件,若满足,则停止迭代,输出划分隶属矩阵U,聚类中心P,迭代次数t;否则,t=t+1,转至Step2.结束条件为到达最大进化代数k,或目标函数|Uk-Uk-1|≤η.
本文方法还涉及平滑参数m及核参数σ的选取.Bezdek给出了参数m的一个经验范围[1.1,5],但没有给出严格的证明[3],通常情况下参数m取值为2.如何对核参数σ进行取值,目前同样缺乏理论支持,更多的是依靠经验取值,通常的解决方法是用一组专门的验证数据集来确定核参数σ.
3.3 算法复杂度分析
本小节对本文算法的算法复杂度进行简要分析.通过对算法步骤进行观察,在整个运算过程中,计算最复杂的过程在Step2根据式(12)计算划分隶属矩阵U.由于算法的具体运算过程与核函数的选取有关,因此这里令基本运算为DK-IFE(xj,pi)/DK-IFE(xj,pk),设m=2,则算法迭代一次,基本运算的计算次数为n·c·c,时间复杂度为T(n)=O(c2·n).算法运行过程中所需保存的数据包括样本集内的n个样本,c个聚类中心以及模糊分类矩阵U,因此算法的空间复杂度为S(n)=O(c·n).
4 实验结果及分析
为了对算法性能进行验证,本文选择不同的样本集合进行试验,为了避免随机误差,每次试验分别进行50次蒙特卡洛仿真.实验前需要对数据进行直觉模糊化处理,在这里使用一种相对简单的算法,即取各维样本最大值的隶属度值为1,其他样本与最大值的比值为其隶属度值,简单起见,令犹豫度为0即可.实验环境:操作系统Window XP,编程软件Matlab7.6,Pentium(R)Core(TM)i7-3770 CPU @ 3.4GHz,3.46 GB的内存.
4.1 同心圆样本聚类实验
采用如下参数方程产生两类交错的同心圆样本进行试验.
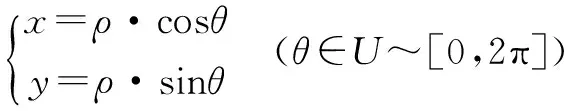
(16)
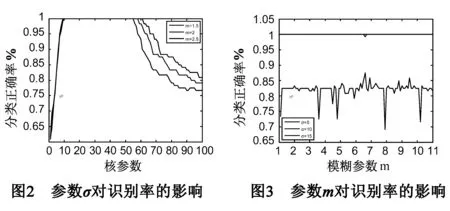
两类样本的半径参数ρ均服从均匀分布,分别为[0,10]和[50,60],总随机产生两类样本共120个.本文选取高斯核作为核函数进行试验,由于不同的核参数σ的取值对算法的影响较大,本文专门取出一组验证数据集对核函数σ的取值进行验证.令平滑参数m分别取1.5,2和2.5,迭代误差η=1e-5,最大迭代代数k=200,核参数σ在[1,100]等间隔取样100次,σ对分类识别率的影响如图2所示.为了模糊参数m的取值进行验证,令核参数σ分别取5,10和15,迭代误差η=1e-5,最大迭代代数k=200,模糊参数m在[1.1,11]等间隔取样100次,m对分类识别率的影响如图3所示.
经过验证,令模糊参数m=2.5,高斯核参数σ=10,迭代误差η=1e-5,最大迭代代数k=200.为了验证算法的有效性,我们将IFCM算法[7]、FKCM算法[11]、IFKCM算法[12]、ILKFCM算法[14]和本文方法(K-IFCM)进行对比.按设定参数进行50次蒙特卡洛仿真实验,实验结果如下表1所示.
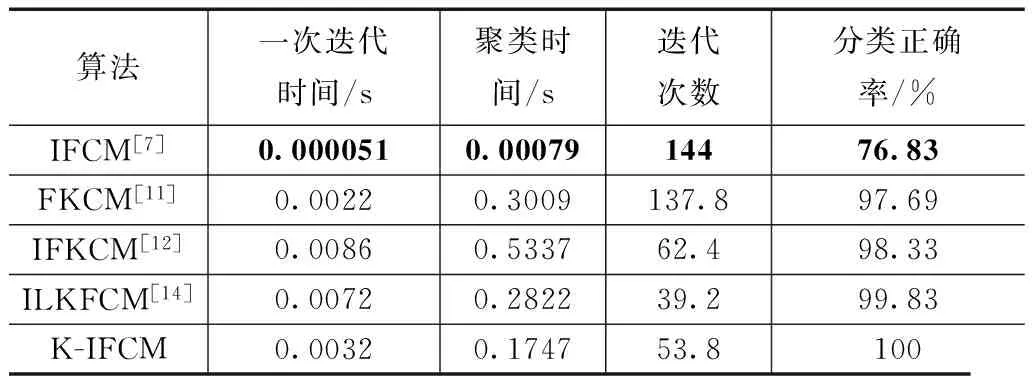
表1 各算法聚类性能对比
4.2 Iris数据集聚类实验
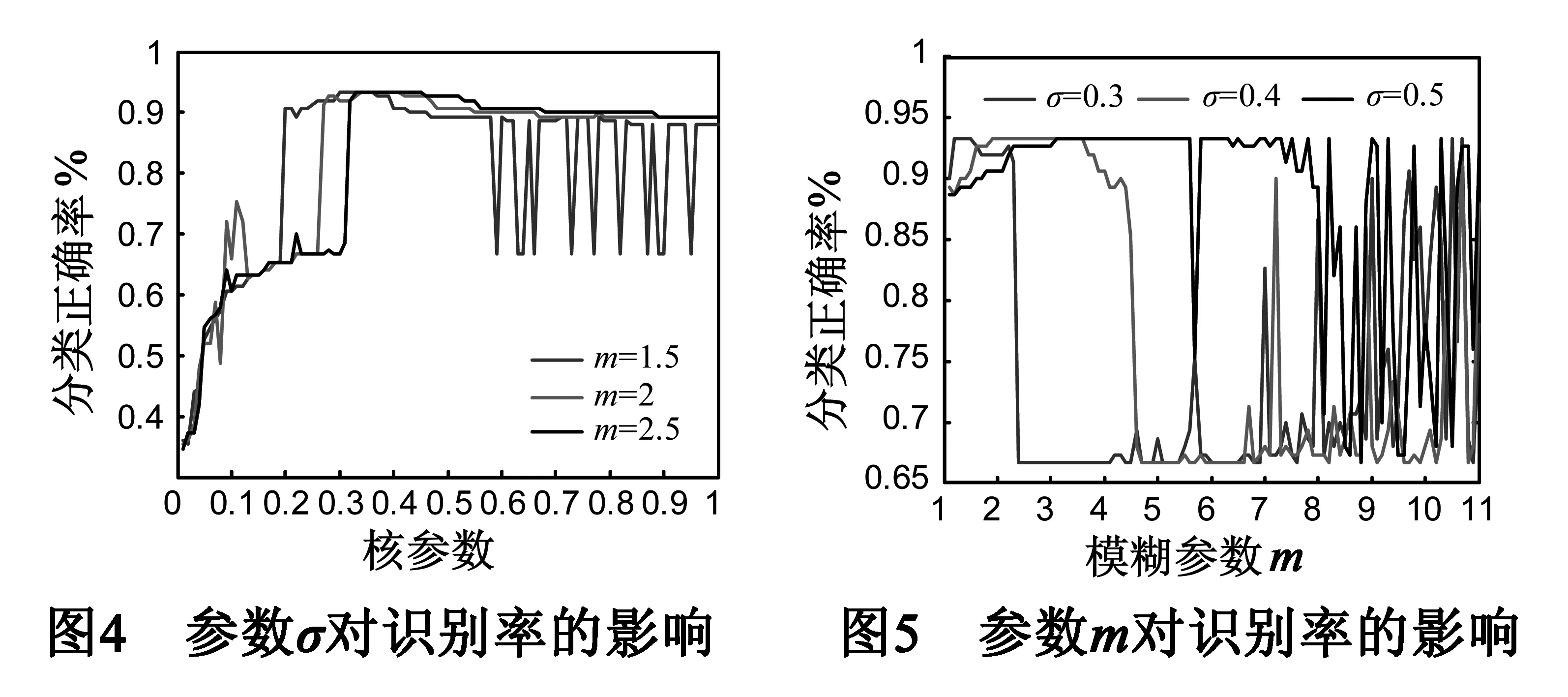
为了验证算法在实际数据集上的聚类性能,选择UCI数据集中经典的Iris数据集对进行仿真实验.实验选取高斯核作为核函数进行试验,令平滑参数m分别取1.5,2和2.5,迭代误差η=1e-5,最大迭代代数k=200,核参数σ在[0.01,1]等间隔取样100次,σ对分类识别率的影响如图4所示.为了模糊参数m的取值进行验证,令核参数σ分别取0.3,0.4和0.5,迭代误差η=1e-5,最大迭代代数k=200,模糊参数m在[1.1,11]等间隔取样100次,m对分类识别率的影响如图5所示.
经过验证,令高斯核参数σ=0.4,模糊参数m=2,迭代误差η=1e-5,最大迭代代数k=200.为了验证算法的有效性,我们将本文方法与IFCM算法[7]、FKCM算法[11]、IFKCM算法[12]、ILKFCM算法[14]、Ng-Jordan谱聚类算法[16]及进行对比.按设定参数进行50次蒙特卡洛仿真实验,实验结果如下表2所示.

表2 各算法聚类性能对比
4.3 实验结果分析
从以上两组实验的参数验证情况来看,核参数σ相对模糊参数m对识别率的影响更大;甚至当核参数σ取到一定值时,改变模糊参数m不会对算法的识别率产生影响.此外,模糊参数m在[1.1,5]之间取值时,算法的识别率较为稳定,这与Bezdek给出了模糊参数m的经验范围吻合.
从第一组对人工同心圆数据的实验结果来看,IFCM算法虽然所需的聚类时间较短,但不具备发现非凸聚类结构的能力,分类效果最差.引入核方法后,FKCM算法虽然也取得了较好的聚类效果,但因其隶属度单一的缺陷,其分类的成功率仍然无法令人满意.而IFKCM算法的正确率则相对一般,要逊于ILKFCM算法及K-IFCM算法,且算法的一次迭代时间最长,这是由于IFKCM算法虽然也把核方法引入到直觉模糊聚类算法,但在具体计算时,为方便计算令样本相对各类别隶属度之和为1,明显违背了直觉模糊思想,再将分类样本与聚类中心的关系推广为直觉模糊关系时,又大大增加了算法的时间复杂度.ILKFCM算法正确率与K-IFCM算法基本相当,但其一次迭代时间则相对K-IFCM算法较长.这是因为ILKFCM算法在目标函数中引入了一个权重模糊因子,提高算法的分类精度的同时也导致了计算量的增加.K-IFCM算法则充分结合了IFCM及FKCM两者算法的优点,将FKCM算法拓展到直觉模糊领域后,获得了更多的样本分类信息,聚类效果最好.同时,本文算法仅是改变了样本间距离度量函数,与其他核方法相比,算法的时间复杂度相对较小.此外,第二组对Iris数据集的实验中我们增加了与Ng-Jordan谱聚类算法的对比,本文方法无论是聚类精度还是时间复杂度上均要优于Ng-Jordan谱聚类算法,其余实验结果与前两组对人工样本的实验结果基本吻合,说明对该算法在实际数据集上同样具有更好的聚类效果.
5 结论
本文将核方法与直觉模糊聚类算法进行有效结合,通过提出一种基于核的直觉模糊欧式距离,并以此作为直觉模糊聚类算法的距离度量,给出了一种基于核化距离的直觉模糊c均值聚类算法,解决了原有直觉模糊c均值聚类算法无法发现非凸聚类结构的问题.实验阶段对核参数σ和平滑参数m的选取进行了探讨,从实验结果分析,本文方法在聚类性能上要优于其他聚类算法.但是,该算法仍有一些需要改进及完善的地方,如引入核方法后,造成了算法时间复杂度的增加.此外,如何根据聚类样本集选取参数均是下一步亟待解决的问题.
[1]Ruspini E H.A new approach to clustering[J].Information and Control,1969,15(1):22-32.
[2]Ceccarelli M,Maratea A.Improving fuzzy clustering of biological data by metric learning with side information[J].Int'l Journal of Approximate Reasoning,2008,47(1):45-57.
[3]Bezdek J C.Pattern recognition with fuzzy objective function algorithms[M].New York:Plenum Press,1981.
[4]雷英杰,王宝树,苗启广.直觉模糊关系及其合成运算[J].系统工程理论与实践,2005,25 (2):113-118,133.
Lei Y J,Wang B S,MIAO Q G.On the intuitionistic fuzzy relations with compositional operations[J].Systems Engineering Theory and Practice,2005,25 (2):113-118,133.(in Chinese)
[5]Song Y F,Wang X D,Lei L,Xue A J.Combination of interval-valued belief structures based on intuitionistic fuzzy set[J].Knowledge-Based Systems,2014,67:61-70.
[6]余晓东,雷英杰,孟飞翔,雷阳.基于PS-IFKCM的弹道中段目标识别方法[J].系统工程与电子技术,2015,37(1):17-23.
Yu X D,Lei Y J,Meng F X,Lei Y.Techniques for target recognition based on particle swarm-based intuitionistic fuzzy kernel clustering[J].Systems Engineering and Electronics,2015,37(1):17-23.(in Chinese)
[7]贺正洪,雷英杰.直觉模糊C均值聚类算法研究[J].控制与决策,2011,26(6):847-850,856.
He Z H,Lei Y J.Research on intuitionistic fuzzy C-means clustering algorithm[J].Control and Decision,2011,26(6):847-850,856.(in Chinese)
[8]Cortes C,Vapnik V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.
[9]Saket A,Sushil M,Oncel T,Peter M.Semi-supervised kernel mean shift clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2014,36(6):1201-1215.
[10]Nikhil R P,Kaushik S.What and when can we gain from the kernel versions of c-means algorithm?[J].IEEE Transactions on Fuzzy Systems,2014,22(2):363-379.
[11]Girolami M.Mercerkernel based clustering in feature space[J].IEEE Trans on Neural Networks,2002,13(3):780-784.
[12]范成礼,邢清华,付强,等.基于直觉模糊核聚类的弹道中段目标识别方法[J] 系统工程与电子技术,2013,35(7):1362-1367.
Fan C L,Xing Q H,Fu Q,et al.Technique for target recognition in ballistic midcourse based on intuitionistic fuzzy kernel clustering[J].Systems Engineering and Electronics,2013,35(7):1362-1367.(in Chinese)
[13]PiciarelliC,Micheloni C,Foresti G L.Kernel-based clustering[J].Electronics Letters,2013,49(2):113-114.
[14]XiangD L,Tang T,Hu C B,Li Y,Su Y.A kernel clustering algorithm with fuzzy factor:application to SAR image segmentation[J].IEEE Geoscience and Remote Sensing Letters,2014,11(7):1290-1294.
[15]Gong M G,et al.Fuzzy c-means clustering with local information and kernel metric for image segmentation[J].IEEE Transactions on Image Processing,2013,22(2):573-584.
[16]Ng A Y,Jordan M I,Weiss Y.On spectral clustering:analysis and an algorithm[A].Proceedings of Advances in Neural Information Processing Systems[C].Cambridge,MA:MIT Press,2002.849-856.

余晓东 男,1989年出生,江西九江人,空军工程大学博士研究生,主要研究方向为模式识别、智能信息处理等.
E-mail:1438894571@qq.com

雷英杰 男,1956年出生,陕西渭南人,空军工程大学教授,博士生导师,主要研究方向为智能信息处理与智能决策.
Intuitionistic Fuzzy c-means Clustering Algorithm Based on Kernelled Distance
YU Xiao-dong,LEI Ying-jie,SONG Ya-fei,YUE Shao-hua,SHEN Xiao-yong
(AirandMissileDefenseCollege,AirForceEngineeringUniversity,Xi’an,Shaanxi710051,China)
The intuitionistic fuzzyc-means clustering algorithm cannot discover the non-convex cluster structure.To alleviate this problem,an intuitionistic fuzzyc-means clustering algorithm based on kernelled distance is proposed.By defining the intuitionistic fuzzy Euclid distance,we map the sample to a high-dimension feature space.So the former features can be reflected thoroughly,which is helpful for clustering.Experiments executed on one artificial data sets and one UCI data sets demonstrate the performance of the proposed method.Compared with the five classical cluster algorithms,our method is of obvious effectiveness and superiority.
intuitionistic fuzzy set;intuitionistic fuzzy clustering;kernel method;unsupervised learning
2015-02-04;
2015-06-08;责任编辑:李勇锋
国家自然科学基金(No.61272011,No.61309022);陕西省自然科学青年基金(No.2013JQ8031)
TP182;TP391
A
0372-2112 (2016)10-2530-05
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.10.035
