基于APT潜伏攻击的网络可生存性模型与分析
2016-12-08关建峰张宏科
姚 苏,关建峰,潘 华,张宏科
(1.北京交通大学电子信息工程学院,北京 100044;2.中国航空综合技术研究所,北京 100028;3.北京邮电大学,北京 100876)
基于APT潜伏攻击的网络可生存性模型与分析
姚 苏1,2,关建峰3,潘 华2,张宏科1
(1.北京交通大学电子信息工程学院,北京 100044;2.中国航空综合技术研究所,北京 100028;3.北京邮电大学,北京 100876)
基于传统网络攻击模式和高级持续性威胁(Advanced Persistent Threat,简称APT)攻击模式提出网络可生存性的评估模型.建立网络攻击场景,仿真验证提出的网络可生存性模型,并比较两种模式的性能.得到的结论:提出的评估模型合理刻画了网络可生存性的两个重要参数,网络攻击传播速率和网络修复速率;基于APT潜伏攻击模式下的网络可生存性性能低于传统攻击模式.
潜伏攻击;网络可生存性;评估模型;马尔科夫链
1 引言
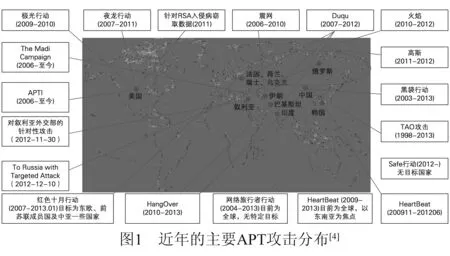
高级持续性威胁(Advanced Persistent Threat,简称APT)是目前计算机网络安全界关注的最热门话题之一[1].特别是2010年谷歌宣布遭受极光攻击[2],伊朗核设施遭受震网(Stuxnet)病毒攻击等一系列极具破坏性的事件[3],打破了人们对传统网络攻击的认识,如震网病毒已经造成伊朗核电站推迟发电.从图1所示的APT攻击[4],可以看出,APT攻击已经成为近年来网络攻击的主要手段之一.
“潜伏性和持续性”是APT攻击最主要的特征[5].“潜伏性”表示APT攻击并非进入用户网络中就立即发动攻击,通常会有一个潜伏期,这个潜伏期可长可短.在潜伏期内,不断收集各种信息,直到收集到重要情报,能彻底掌握所针对的目标人、事、物.因此,APT攻击模式实质上是一种“恶意商业间谍威胁”.“持续性”体现在网络攻击者不断尝试各种攻击手段,以及渗透到网络内部后长期蛰伏,继而不断发动攻击,从而达到破坏用户网络的目的[5].
目前,针对APT网络攻击的研究还处于初级阶段,开展的研究主要在APT攻击的案例分析[7]、特征值提取[8]、检测机制[9]等方面,并没有从网络可生存性的角度分析.
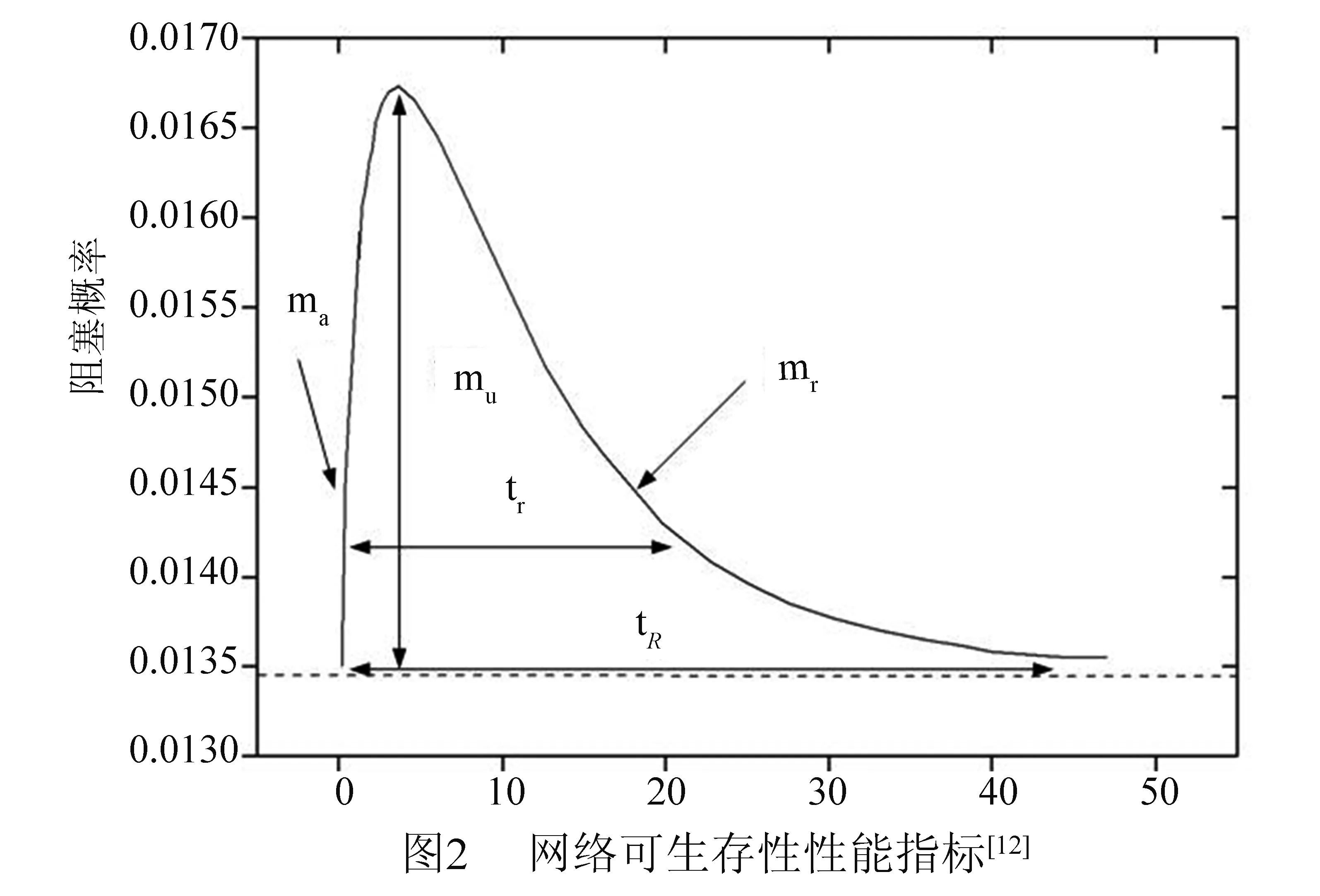
网络可生存性(Network Survivability)[10]泛指网络在出现故障损坏、遭受攻击或不可预知的事故时,仍然能够及时完成关键任务(提供服务)的能力,它属于网络安全性和可靠性的一部分.目前,国内外对于网络可生存性并未有统一的定义,不过得到广泛共识的是美国国家标准学会(American National Standards Institute,简称ANSI) T1A1.2网络可生存性标准委员会给出的定义[11],网络可生存性包括两个方面:(1)在网络出现故障的情况下,通过各种恢复技术,来维持或恢复网络服务使之达到可接受的状态;(2)网络通过应用预防技术,从故障节点中减轻或预防服务失效.可生存性通常用生存率来表示,即当某条链路或者节点出现故障时,可从其它链路上疏通的业务量与该链路所传送的业务量之比.图2给出的可生存性量化指标的说明[12].X轴表示时间,Y轴表示网络的可生存性.该曲线刻画了网络遇到故障或者攻击时,网络可生存性度量值即阻塞概率随着时间产生的变化.在故障或攻击发生之前,阻塞概率为ma;故障或攻击发生后,经过时间tr后,阻塞概率为mr;经过时间tR后,阻塞概率恢复到ma.
目前,针对网络可生存性的研究主要集中在故障或者意外事故前提下开展的研究[13,14].如文献[13] 提出了一种基于飓风灾难条件下的网络可生存性模型,采用连续时间马尔科夫链的分析方法,详细分析了灾难传播和恢复过程,并总结了三种不同的灾难恢复机制.文献[14]改进了文献[13]提出的连续时间马尔科夫链分析方法,并提出了一种基于地震灾难条件下的网络可生存性模型,并与实际情况比较,验证了该模型的合理性.文献[15]在注重提高网络可生存性的同时,也兼顾服务可区分性的要求,提出了一种主动服务漂移的模型,增强了对不同网络环境的可生存性适用性.文献[16]针对大规模网络场景下提出了一种提高网络可生存性方法,文献[17]给出了网络可生存的评估体系.可以看出,针对网络攻击特别是新的网络攻击(诸如APT攻击)的特点,而开展的网络可生存性研究较少.本文结合APT攻击的隐蔽性特点,即网络中的节点被攻击后有潜伏期特点,构建APT攻击下的网络可生存性模型,并对分析了其网络可生存性性能.
本文第二节叙述APT攻击下的网络生存性模型;第三节简要介绍在APT攻击下使用该模型对网络生存性分析;第四节验证网络可生存性模型的正确性,仿真APT攻击下的网络生存性指标并与传统攻击模式进行比较;第五节提出建议并进行总结.
2 模型建立
2.1 网络可生存性模型
由于攻击是包含时间序列的单个事件,为了评估和分析网络遭受攻击时的可生存性,本文研究定量评估模型,给出一种网络可生存性模型.
假设该攻击初始于接入网的某个子网,之后攻击传播到下一个子网,之后依次传播.这种传播可以称作攻击传播,它是一种级联状行为.不同于故障的传播特点,网络攻击传播可以发源于内部网络,并且有多个状态.
此外,网络可以被看作有一个包含节点和有向边的有向图.节点表示网络中基础设施(终端、路由设备等),有向边表示信息传播的方向.网络系统的脆弱性表现为攻击的初始状态和传播状态都是基于某个随机事件.因此,这种传播过程可以被视为随机过程.
假设网络的节点数量为n,攻击事件将有以下几个步骤.不失一般性,网络攻击最初发生于节点1.接着,在一个随机时间内,攻击从被感染的节点传播到下一个节点,节点间的攻击传播视为有向边.这种传播被视为“无记忆”性的,攻击事件从一个节点传播到另一个节点仅依赖于当前的系统状态,而与系统的历史状态无关.由于攻击的传播速度和方向是由外部攻击源等条件决定的因此遭受攻击的节点可以在一个随机时间内被修复.假设攻击的传播速率和修复时间服从指数分布,本文的研究重点在网络初始被攻击,攻击传播直至网络系统完全被修复的传播时段,其过程符合连续时间的马尔科夫随机过程的约束条件.
假设在有限状态空间S= {1,2…,n}中{X,t>0}表示网络系统中的各个节点的状态.每一个接入网都有n个不同区域的子网组成.网络攻击在整个网络中传播.在任意时刻t,网络系统的状态可以由以下n维向量表示
X(t)=(X1(t),X2(t),…Xn(t)),t≥0
(1)
对于子网k∈{1,2,…,n},Xk(t)表示在时刻t子网k的状态.对于子网k,它有两种状态,一种是遭受攻击的状态“0”,另一种是正常状态“1”.当网络攻击未发生时,此时子网k状态为正常状态“1”;当子网k在时刻t遭受攻击时,此时子网状态由正常状态“1”变为“0”;经过时间t′,子网k由状态“0”修复为“1”.
(2)
此外,每次只能对一个子网发动攻击;在本文中,子网作为最小的网络系统单位,只有当子网完全被攻击后,子网才开始修复过程;攻击和修复的传播过程只取决于当前子网状态,而与到达当前状态的路径没有关系.
根据上述假设,攻击传播过程中的子网状态X(t)可以被看作为一个连续时间的马尔科夫链,它的状态空间为:
Ω={(X1,X2,…,Xn),X1,X2,…,Xn∈(0,1)}
(3)
状态空间Ω总共包含N=2n个状态.子网状态X(t)从(0,1,…,1)开始,结束于(1,1,…,1),这表明网络中所有子网都依次遭受到攻击,并且依次恢复到正常状态.
简而言之,网络可生存的模型可以归纳为以下几点:
(1)在某时刻t,子网的状态只有两种状态{0,1};
(2)在初始时刻t=0,第一个子网遭受攻击,此时网络的状态为(0,1,…,1);
(3)攻击从子网k-1传播到子网k服从泊松随机过程,传播的速率为λk;
(4)每个子网只有一次修复过程并且子网中的终端都可以同时被修复完成,子网k的平均修复速率服从指数分布值为μk.
根据上述的假设,在状态空间S,子网的修复过程可以从数学上建模为时间上均匀分布的连续时间马尔科夫链(Continuous-Time Markov Chain,CTMC).
对每个状态而言,有t≥0和i∈S,我们定义t时刻处于状态i的概率为:
πi(t)=Pr{X(t)=i}
(4)
假设X(t)的传播概率的列向量为
π(t)=[π1(t),π2(t),…,πN(t)]
(5)
当系统处于状态i∈S,ψi为系统的回报率.因此,根据连续时间马尔科夫链的状态空间,系统的回报率也可用列向量表示为:
ψ=[ψ1,ψ2,…,ψN]
(6)
根据上述模型,可以有多种测算方式来测算网络的可生存性性能.由于无法在系统修复期间准确预估系统的状态,我们考虑从正常工作的网络系统中获取性能指标的预估值.在我们的模型中,系统的回报作为系统性能的重要指标.在时刻t网络可生存性性能由系统瞬时的预估回报E[M(t)]表示:
(7)
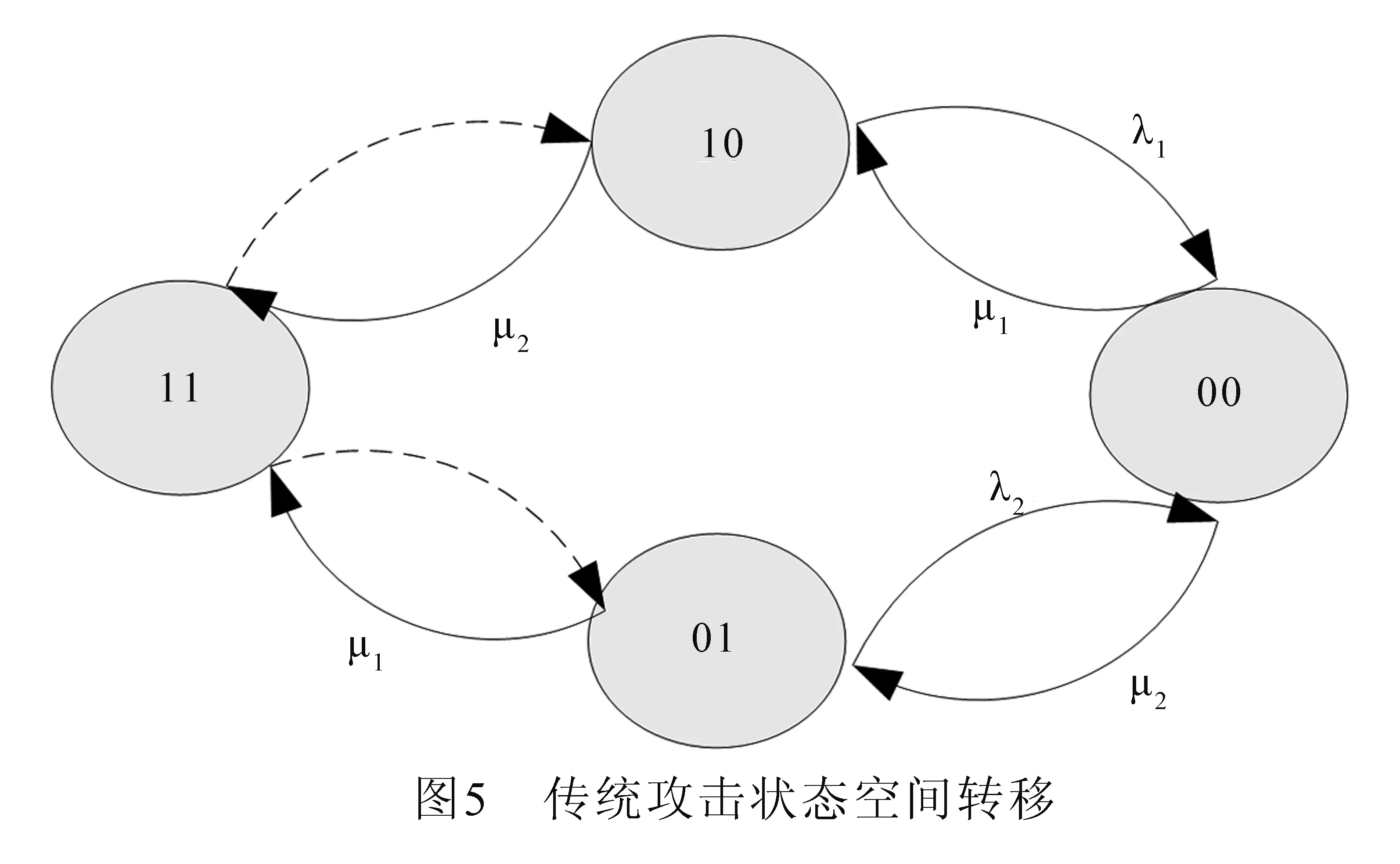
假设系统是有序的,在状态1,2,…,k(k (8) 其中,pij表示状态i转移到状态j的转移概率. 根据状态转移矩阵P,连续时间马尔科夫链的动态行为可以由柯式差分微分方程表示: (9) 则状态转移概率矩阵π(t)为 (10) 2.2 APT潜伏攻击模式的网络可生存模型 APT潜伏攻击模式,网络攻击并非一触即发的,通常会潜伏在所攻击的网络系统,并在某个时刻触发,方才发动攻击,它的攻击更具有隐蔽性并且破坏性更强.因此,不同于正常状态,对于子网k∈{1,2,…,n},Xk(t)表示在时刻t子网k的状态.此时,对于子网k,它有三种不同状态:(1)健康状态“1”;(2)遭受APT攻击后的休眠状态“0”;(3)遭受APT攻击后的活跃状态“0′”[18]. (11) 如图3所示,当网络攻击未发生时,此时子网k状态为健康状态“1”;当子网k在某时刻t遭受攻击时,此时子网状态由健康状态“1”进入休眠状态“0”;再经过时间t′,子网k由休眠状态“0”进入活跃状态为“0′”;此时,子网探测到来自外部的APT攻击,开始进行修复;经时间t″,子网k由活跃状态修复为健康状态. 同样,APT攻击下的攻击传播过程中的子网状态X(t)也可以被看作为一个连续时间的马尔科夫链,它的状态空间为: Ω={(X1,X2,…,Xn),X1,X2,…,Xn∈(0,0′,1)} (12) 状态空间Ω总共包含N=3n个状态.子网状态X(t)从(0,1,…,1)开始,结束于(1,1,…,1).攻击从正常状态子网k-1传播到休眠状态子网k服从泊松随机过程,传播的速率为λk;同样,攻击从休眠状态子网k-1传播到活跃状态子网k服从泊松随机过程,传播的速率为λk′. 本节基于上述模型,构建攻击场景,分析和评估攻击和修复状态的传播过程. 攻击场景的示意图如图4所示.该网络系统由核心网和接入子网组成.接入子网由接入路由器接入核心网中,为简化分析和评估过程,假定只有两个接入子网,每个子网中的终端数量分别为N1和N2.初始状态,假设接入子网1遭受攻击,紧接着攻击传播至接入子网2. 3.1 传统攻击模式 在上述攻击场景的传统攻击模式下,状态空间S={S0,…,Sθ}(θ=22-1)有四种不同状态,其传播状态可以用(X1,X2)表示,其中子网状态Xi∈{0,1}.可能存在的传播状态为: S0= (11),S1= (10),S2= (01),S3= (00). 如图5所示,假设接入子网1被攻击,子网1所有的终端都将与接入路由器断开连接.此时,接入子网空间的状态为(01).在该状态,若接入子网2继续被攻击,且攻击传播速率为λ2,子网进入(00)状态;若接入子网1被修复,且修复速率为μ1,子网恢复至健康状态(11).同样,如果初始时刻,子网2遭受攻击,子网空间状态则为(10);在该状态,若子网1被攻击,则进入(00)状态;若子网2被修复,则进入健康状态(11). 当子网状态为(00),它只能进入修复过程;当修复速率为μ1,子网状态恢复至(10);当修复速率为μ2,子网状态恢复至(01). 在时刻t的传输状态概率为 π(t)=[π(0,1)(t)…π(X1,X2)(t)…π(1,1)(t)] (13) 根据状态转移图我们容易得到,传统攻击模式下的状态转移矩阵为: (14) (15) 3.2 APT攻击模式 在APT攻击模式下,子网空间状态有正常、休眠和活跃三种.基于上述攻击场景的连续马尔科夫链的状态转移图如图6所示,该转移图有9个节点.因此,转移矩阵为9*9向量空间,初始概率向量R=(1,0,0,0,0,0,0,0,0). 定义向量空间S={S0,…,Sθ}(θ=32-1),每个状态空间可以由(X1,X2)表示,其中Xi∈{0,0′,1}.状态空间的九个状态分别为: S0=(11)S1=(01)S2=(10)S3=(0′1)S4=(00), 接入子网初始处于正常状态(11),当遭受APT攻击后,攻击源潜入子网中,此时,接入子网进入(10)或者(01)状态.以状态(01)为例,在此状态,攻击源可从子网1传播至子网2,并在子网2中潜伏,此时子网状态为(00),攻击传播速率为λ2;若攻击源在(01)状态被激活,此时对子网1发起APT攻击,则子网状态为(0’1),攻击传播速率为λ1′. 在状态(00),两个子网均被APT攻击潜伏,在此状态下,若攻击传播速率为λ1′,则表示子网1被攻击,子网状态进入(0′0);若攻击传播速率为λ2′,则表示子网2被攻击,子网状态进入(00′). 在状态(00′),若子网1被激活成活跃攻击状态,则进入(0′0′)状态,攻击传播速率为λ1′;若子网2被修复,修复速率为μ2,则子网状态进入(01).同样,在状态(0′0),子网状态既可进入(0′0′),也可修复为(10). 在状态(0′0′),子网只可进入修复过程.但其修复过程有两种不同路径,一种先修复完成子网1,经过修复速率μ1子网状态进入(10′),最终到达完全正常状态(11);另一种是先修复完成子网2,经过修复速率μ2子网状态进入(0′1),最终到达完全正常状态(11). 在时刻t的传输状态概率为 π(t)=[π(0,1)(t)…π(X1,X2)(t)…π(1,1)(t)] (16) 根据图6我们容易得到,APT攻击模式下的状态转移矩阵为: (17) (18) 为了进一步揭示网络攻击时的网络可生存性传播模型及规律,通过MATLAB软件仿真,取得了该模型的传播曲线,并设定不同参数验证了该模型的正确性.同时,为了方便比较,突出APT攻击时网络可生存的特点,将传统攻击和APT攻击时的传播曲线放在同一张图中对比. 在这里,我们考虑用网络中活跃用户数百分比作为网络生存性的一个标准化性能指标[19],这个指标可以准确反映网络中终端被中断服务的比例.该百分比可以用公式(7)的预期瞬时回报率表示.因而,预期的瞬时回报率可以描述在t时刻网络中的终端被攻击的情况. 假定子网i的用户数为Ni,可以得到每个状态的回报率.例如,传统攻击模式下的回报率为: 考虑到每个C类IP地址最多可连接254台主机,因而我们设置子网1连接的终端数N1=150,子网2连接的终端数N2=200.根据文献[20],我们可以得到网络攻击的传播速率和修复速率.通常,网络的修复速率会比网络攻击速率低一个数量级.因而,设定的网络攻击传播速率和修复速率如表1和表2所示. 下面从两个维度来检验本文提出的网络可生存性模型.首先假设子网初始状态的攻击传播速率均为2hours-1,修复速率均为0.2hours-1,如表1所示.通过增大子网攻击传播速率,如图7所示.从图中可以看出,网络在遭受攻击时,子网中活跃用户数明显下降.但随着时间的推移,子网中的终端逐渐被修复,直至完全被修复(子网的活跃用户百分比为1).根据表2中的参数,当保持子网中修复速率不变,增大子网的攻击传播速率,可以看出,子网中初始活跃用户数不断下降,同时,子网达到完全被修复状态所需要的时间也不断增加.在150hour时刻,初始状态已完全修复,但状态4只修复至0.8. 表1 子网攻击传播速率参数 根据表2中的参数,当子网的攻击传播速率保持不变,通过增大子网的修复速率,如图8所示,子网中初始活跃用户数不断增加,由初始状态0.2增加至状态4的0.4.同时,初始状态需要经过100hour才可完全修复,然而状态4在经过10hour,已经修复至0.9,可见子网修复速率的提升. 表2 子网修复速率参数 由此可知,网络的可生存性性能不仅取决于网络攻击的传播速率,还与网络的修复速率相关. 在APT攻击模式下,将网络攻击传播速率和修复速率参数设置一致,与传统攻击模式的可生存性曲线比较.如图9所示,APT攻击模式下的网络修复速率比传统模式下稍低.这是因为在APT攻击模式下,网络中的攻击具有潜伏性,这样在潜伏期网络攻击不容易被发现,致使网络的可生存性比传统模式要差.但随着时间的推移,网络的活跃用户数也修复至正常水平,从而验证了模型的正确性.但总体上,APT攻击对网络的可生存性是有影响的.综上所述,本文提出的模型有效的刻画了基于APT攻击的网络可生存性特点,具有一定的现实指导意义. 本文基于连续马尔科夫链,建立网络可生存性模型,并通过攻击实例,验证了模型的正确性.总结了影响网络可生存性的两个重要因素,网络攻击传播速率和网络修复速率.更进一步,通过仿真验证APT攻击模式下,网络可生存性的特点.可以看出,网络修复速率是影响APT攻击模式下的网络可生存性性能关键指标,是防御APT攻击的重要保证.下一步,需要继续研究攻击潜伏周期长短对网络可生存性的具体影响,以及针对多个子网发动同时攻击的模型构建和安全策略. [1]Jeun I,Lee Y,Won D.A practical study on advanced persistent threats[J].Computer Applications for Security,Control and System Engineering,2012,11:144-152. [2]Zetter K.Google hack attack was ultra sophisticated,new details show[J].Wired Magazine,2010,14:33-36. [3]Langner R.Stuxnet: dissecting a cyberwarfare weapon[J].IEEE Security & Privacy,2011,9(3): 49-51. [4]肖新光.恶意代码对抗体系演进的四部曲[EB/OL].http:// www.antiy.net/papers/. Xiao X G.The tetralogy of defending malicious code[EB/OL].http:// www.antiy.net/papers/.(in Chinese) [5]Bencsáth B,Pék G,Buttyán L,et al.The cousins of stuxnet: duqu,flame,and gauss[J].Future Internet,2012,4(4): 971-1003. [6]Lee J D.Targeted cyberattacks: a superset of advanced persistent threats[J].IEEE security & privacy,2013,11(3): 54-61. [7]Giura P,Wang W.A context-based detection framework for advanced persistent threats[A].International Conference on Cyber Security [C],Washington,2012.69-74. [8]Dube T E,Raines R A,Grimaila M R,et al.Malware target recognition of unknown threats[J].IEEE Systems Journal,2013,7(3): 467-477. [9]Johnson J R,Hogan E A.A graph analytic metric for mitigating advanced persistent threat[A].IEEE International Conference on Intelligence and Security Informatics[C],Seattle,2013.129-133. [10]Sterbenz J P G,Hutchison D,?etinkaya E K,et al.Resilience and survivability in communication networks: Strategies,principles,and survey of disciplines[J].Computer Networks,2010,54(8): 1245-1265. [11]ANSI T1A1.2 Working Group on Network Survivability Performance.Technical Report on Enhanced Network Survivability Performance[S],ANSI,Tech.Rep.TR No.68,2001. [12]Heegaard P E,Trivedi K S.Network survivability modeling[J].Computer Networks,2009,53(8): 1215-1234. [13]Xie L,Heegaard P E,Jiang Y.Network survivability under disaster propagation: Modeling and analysis[A].Wireless Communications and Networking Conference (WCNC)[C],Shanghai,2013.4730-4735. [14]Xie L,Jiang Y,Heegaard P E.Modelling and analysis of the survivability of telecommunication networks[A].15th International Symposium on Software Reliability Engineering[C],2004,367 - 377. [15]赵二虎,阳小龙,彭云峰,隆克平.CPSM:一种增强IP网络生存性的客户端主动服务漂移模型[J].电子学报,2010,38(9):2134-2139. Zhao E H,Yang X L,Peng Y F,Long K P.CPSM: client-side proactive service migration model for enhancing IP network survivability[J].Acta Electronica Sinica,2010,38(9):2134-2139.(in Chinese) [16]Izaddoost A,Heydari S S.Enhancing network service survivability in large-scale failure scenarios[J].Journal of Communications & Networks,2014,16(5):534-547. [17]王鹏飞,赵文涛,张帆,邹荣念.网络系统可生存能力量化评估的指标体系研究[J].计算机工程与科学,2014,36(6):1050-1056. Wang P F,Zhao W T,Zhang F,Zou R N.Research on index system of quantitative evaluation for network systems viability[J].Computer Engineering&Science,2014,36(6):1050-1056.(in Chinese) [18]Wen S,Zhou W,Zhang J,et al.Modeling propagation dynamics of social network worms[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(8): 1633-1643. [19]Zolfaghari A,Kaudel F J.Framework for network survivability performance[J].IEEE Journal on Selected Areas in Communications,1994,12(1): 46-51. [20]Camtepe S A,Yener B.Modeling and detection of complex attacks[A].Third International Conference on.IEEE Security and Privacy in Communications Networks and the Workshops[C].Nice,2007.234-243. 姚 苏 男,1986年12月出生,安徽舒城人,中国航空综合技术研究所工程师,现为北京交通大学在读博士.目前主要从事网络安全标准应用技术的研究工作.获中航工业集团奖励多项,参与多项国家和军队技术基础研究项目. E-mail: yaosu@bjtu.edu.cn. 关建峰 男,1982年2月出生,河南巩义人.2004、2010年分别毕业于东北大学、北京交通大学获得学士、博士学位.2010年进入北京邮电大学网络技术研究院,主要从事移动互联网、网络安全等方面的研究工作. E-mail: jfguan@bupt.edu.cn. 潘 华 女,1965年10月出生,安徽界首人;1988、1991年分别于北京航空航天大学获得学士、硕士学位,现为中国航空综合技术研究所研究员,主要从事信息技术标准化的研究工作,主编多项国家军用标准,并多次获得军队和中航工业集团奖励. 张宏科 男,1957年9月出生,山西大同人,北京交通大学教授,博士生导师.目前主要从事下一代信息网络关键理论与技术的研究工作,作为首席科学家主持国家973项目"智慧协同网络理论基础研究"的研究工作. Modeling and Analysis for Network Survivability of APT Latent Attack YAO Su1,2,GUAN Jian-feng3,PAN Hua2,ZHANG Hong-ke1 (1.SchoolofElectronicsandInformationEngineering,BeijingJiaotongUniversity,Beijing100044,China;2.ChinaAero-PolytechnologyEstablishment,Beijing100028,China;3.BeijingUniversityofPostsandTelecommunications,Beijing100876,China) The paper proposes the model of network survivability based on the patterns of normal network attack and APT attack.The model is demonstrated by constructing the simulation scenarios of network attack to analyze their performances.The results show that this evaluation model can effectively reflect two parameters: the speeds of network attack propagation and network recovery,and the performance of network survivability of APT attack pattern is lower than that of normal attack pattern. APT;network survivability;evaluating model;Markov chain 4-10-28; 2015-10-30;责任编辑:郭游 国家973重点基础研究发展规划(No.2013CB329101);国家自然科学基金(No.61232017,61003283);国家科技重大专项(No.2013ZX03006002) TP393.0 A 0372-2112 (2016)10-2415-08 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.10.020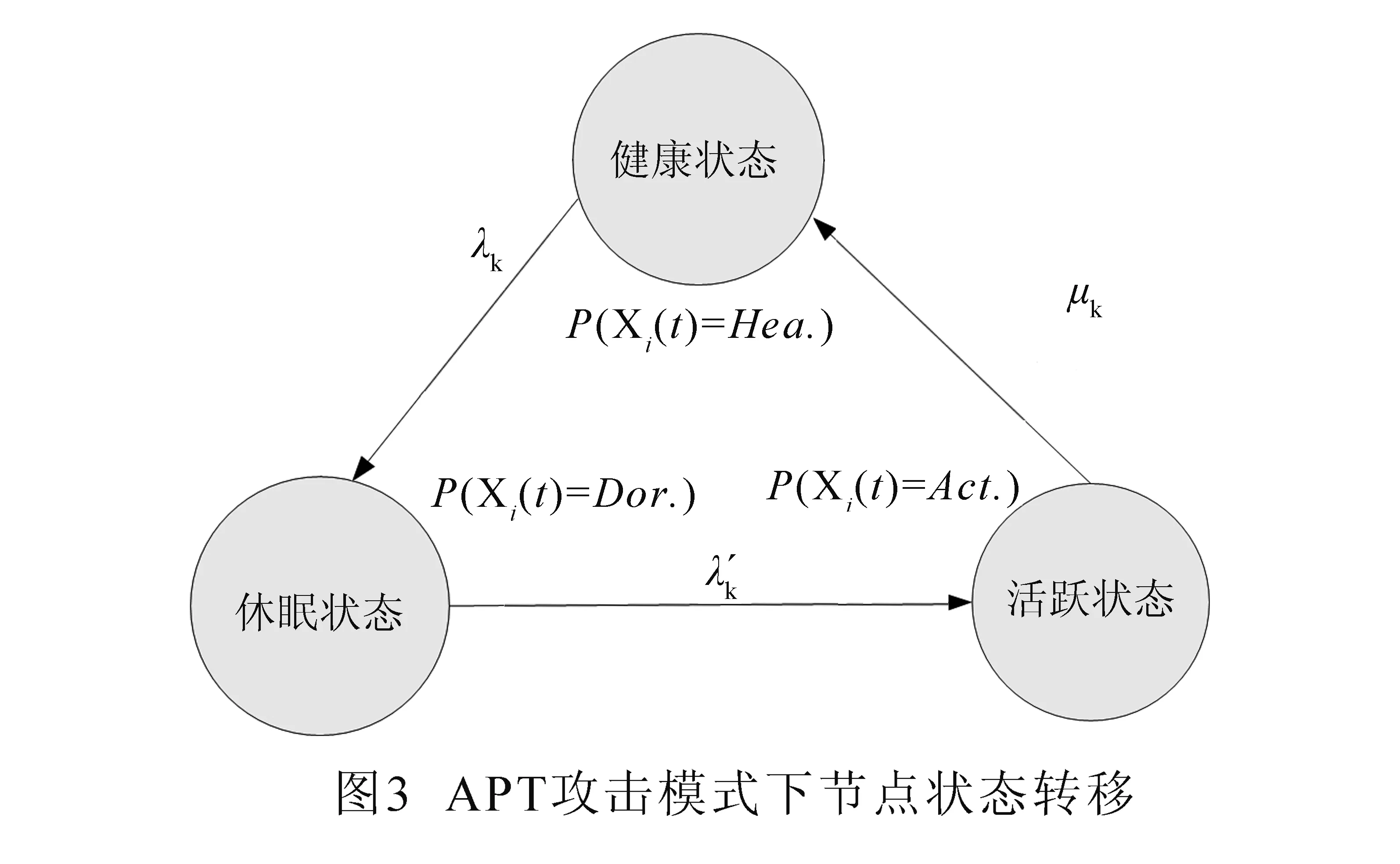
3 攻击实例
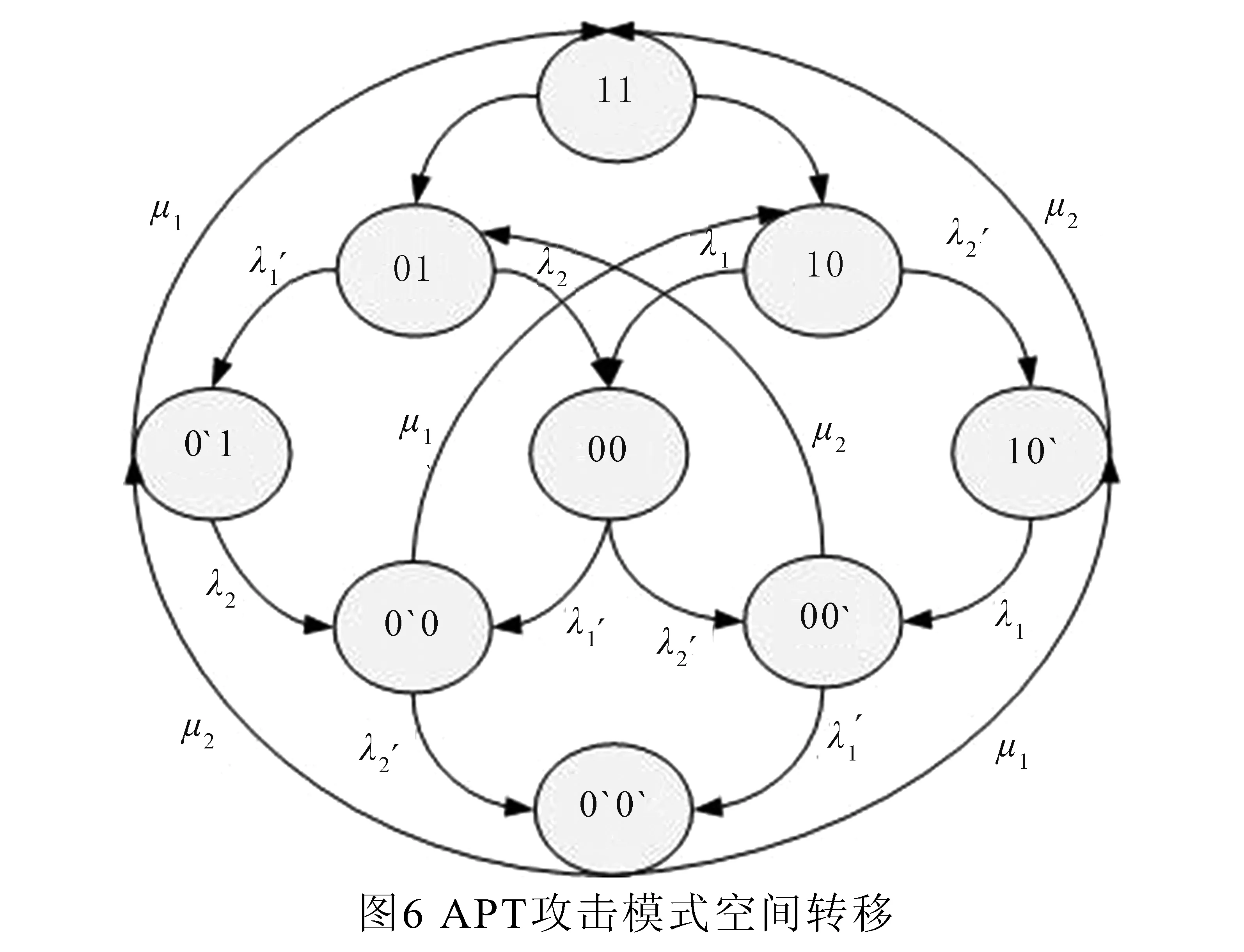
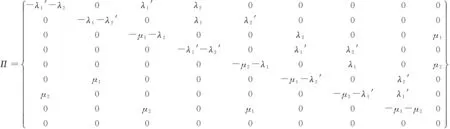
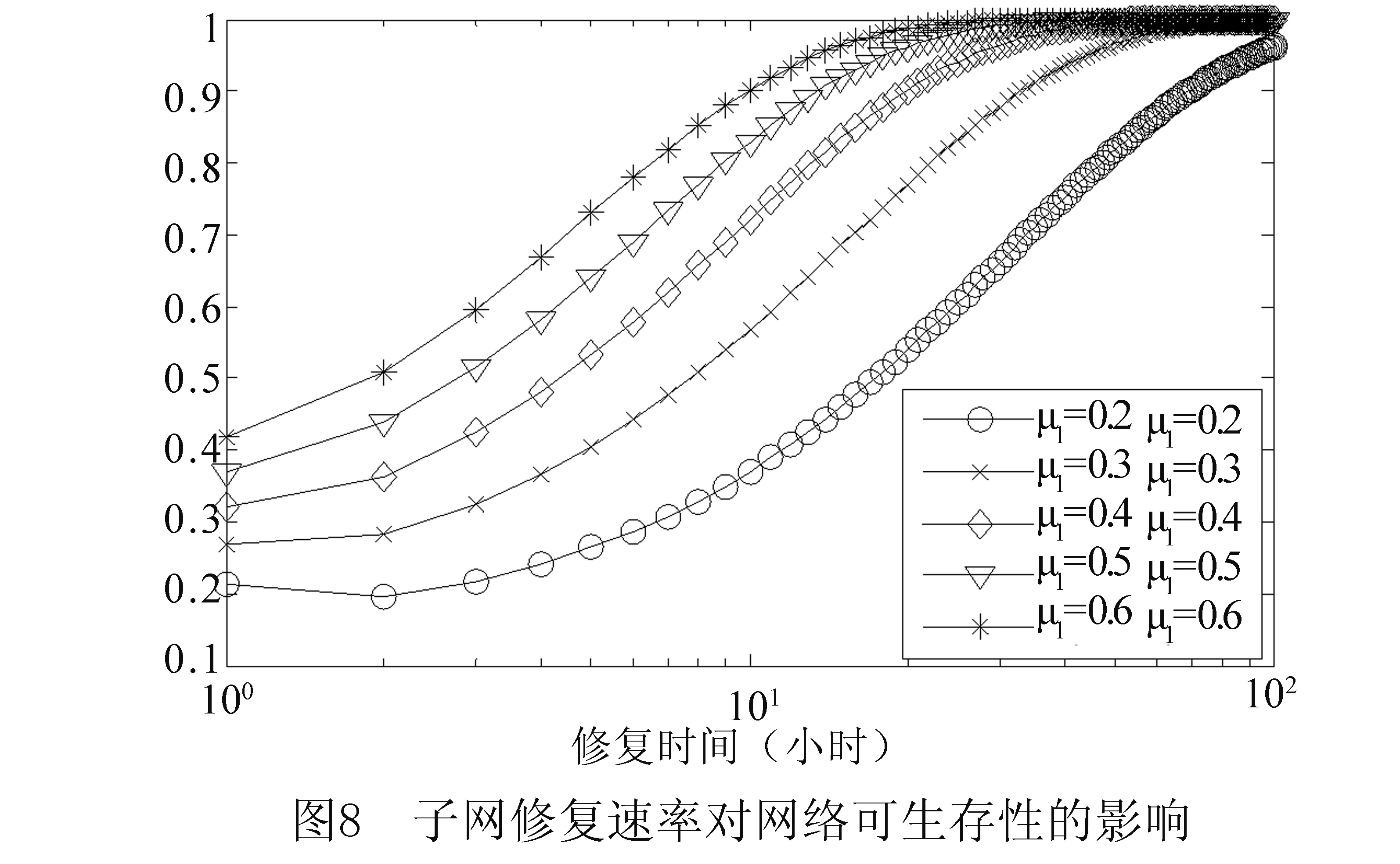
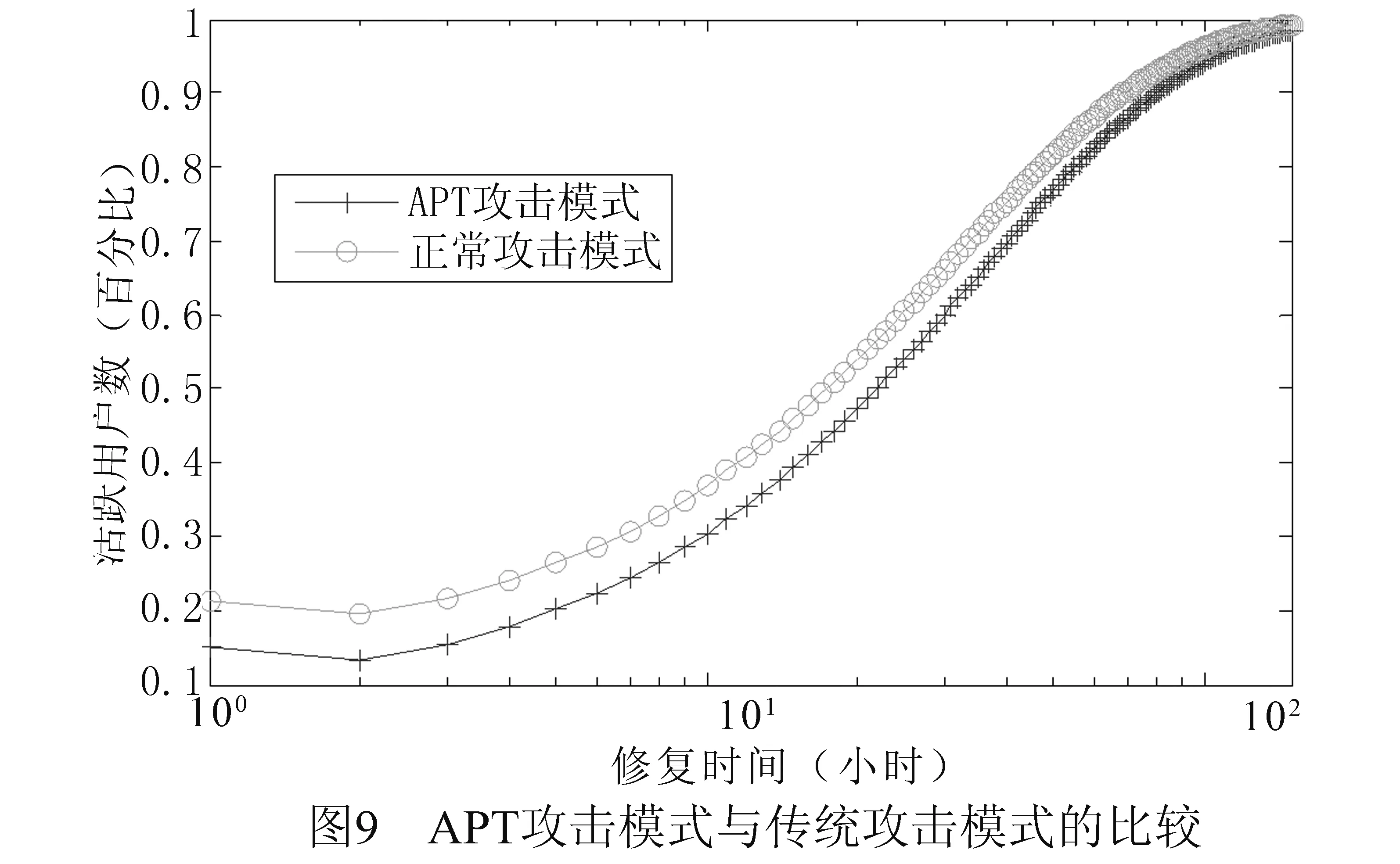
4 仿真与分析
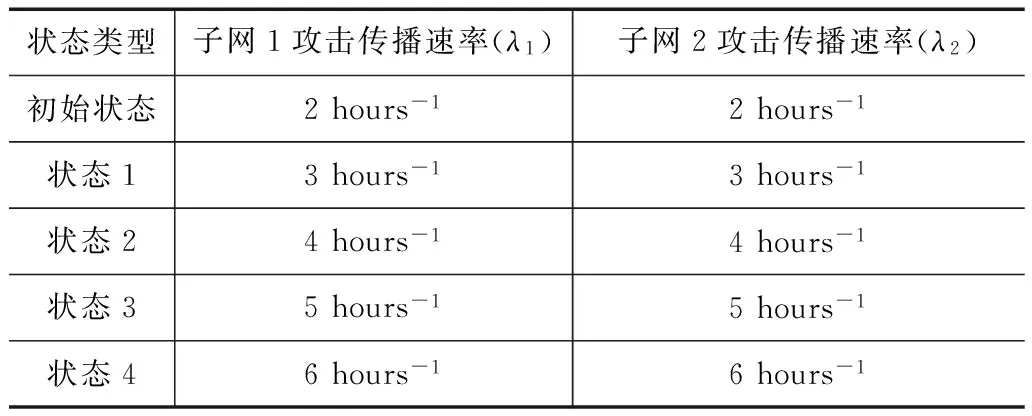
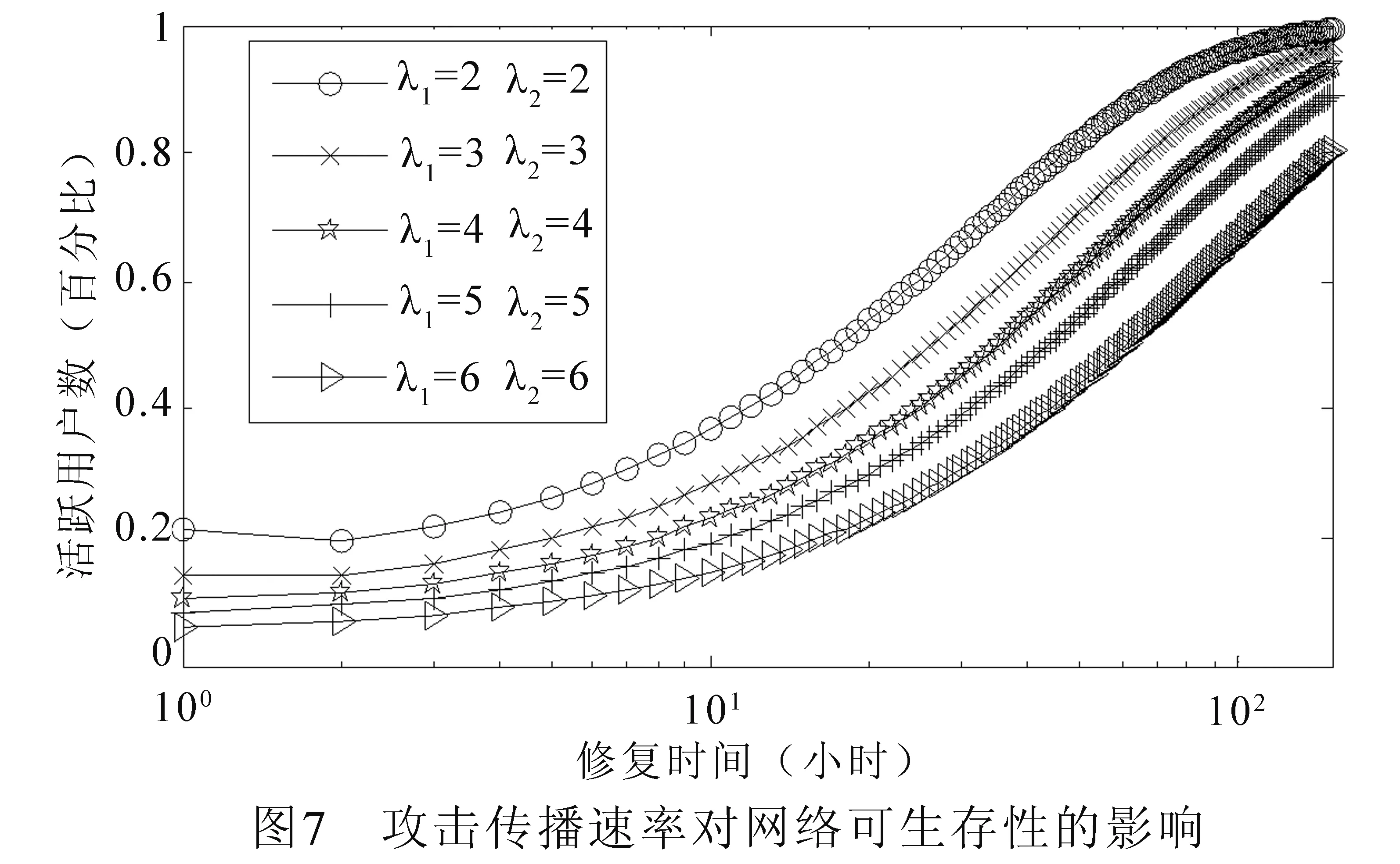
5 结论




