新生目标强度未知的单量测PHD滤波器

徐从安,熊 伟,刘 瑜,何 友

(海军航空工程学院信息融合研究所,山东烟台264001)



新生目标强度未知的单量测PHD滤波器

徐从安,熊 伟,刘 瑜,何 友

(海军航空工程学院信息融合研究所,山东烟台264001)

自适应新生目标强度PHD滤波器(PHD-M)在目标漏检时易发生错估或漏估,从而导致滤波器估计性能下降.为解决这一问题,提出了一种新生目标强度未知的单量测(single measurement)PHD滤波器(PHD-SM)并给出了其粒子实现方式.该文首先通过构建一步虚拟量测对漏检目标进行补偿,然后基于单量测PHD分解技术推导了PHD预测和更新公式,最后设计了一种无须聚类操作的多目标状态估计方法.仿真实验表明,在当检测概率PD较小时,PHD-SM滤波器估计性能优于PHD-M滤波器,且检测概率越小,性能优势越明显.

多目标跟踪;概率假设密度;新生目标强度未知;单量测;一步虚拟量测

1 引言

由于目标数目和量测信息的不确定性,如何在杂波背景下准确估计目标数目并进行稳定跟踪,一直是目标跟踪领域研究的难点问题之一.传统的多目标跟踪方法主要有最近邻(Nearest Neighbor,NN)[1]、联合概率数据关联(Joint Probability Data Association,JPDA)[2,3]和多假设跟踪(Multiple Hypothesis Tracking,MHT)[4]等方法,这些方法通常假定目标个数已知或未知恒定,通过数据关联,将多目标跟踪转化为单目标滤波跟踪,但当目标密集或虚警较多时,数据关联会带来组合爆炸、关联误差等问题,此时这些方法往往跟踪效果较差[5,6].

近年来,以Mahler为代表的研究者开始将随机有限集(Random Finite Set,RFS)理论应用于多目标跟踪,其中最具代表性的是概率假设密度(Probability Hypothesis Density,PHD)滤波器[7],该滤波器能够避免复杂的数据关联,尤其适合解决未知时变的多目标跟踪问题,具有较高的研究价值.由于求解目标PHD过程存在复杂的集合积分运算,限制了PHD滤波器的推广和应用.针对PHD滤波器的实现问题,目前主要有高斯混合PHD[8]和粒子PHD[9].高斯混合PHD基于线性高斯假设,具有闭合的解析表达式,这使得实时性处理变得容易.粒子PHD虽适用于非线性非高斯系统,但其性能严重依赖于聚类算法.结合上述两种实现形式的优缺点,在具体应用中出现了很多变体改进[10～14].

传统PHD滤波器假定新生目标强度已知,而实际背景中目标可能在视场中任何位置出现,此时传统PHD滤波器不再适用.为此,Ristic等提出了基于量测驱动的自适应新生目标PHD滤波器(Measurement-driven PHD,PHD-M)[15,16],但该滤波器存在归一化失衡问题,同时,在检测概率较低时存在漏估或错估的问题.文献[17]解决了PHD-M滤波器的归一化失衡问题,并给出了其高斯混合实现.为解决检测概率较低时PHD-M存在的漏估问题,本文提出一种新生目标强度未知的单量测PHD滤波器(Single Measurement PHD,PHD-SM),该滤波器利用量测生成新生目标粒子,通过构建一步虚拟量测对漏检目标进行补偿,然后采用单量测PHD分解技术对目标PHD进行预测和更新.在对滤波器进行粒子实现时,由于利用聚类技术估计目标状态的不可靠性[18],文献[15]提出一种无须聚类操作的方法,但该方法缺少对漏检目标的补偿,同时也未对权值分解过程进行分析.为此本文给出一种新的状态估计方法,该方法对权值分解进行分析,利用一步虚拟量测对漏检目标进行补偿,在避免聚类操作的同时,能够对漏检目标进行有效估计.

2 PHD-M滤波器及其粒子实现

PHD-M滤波器[16]在目标新生时刻将目标划分为存活目标和新生目标,并分别对两类目标进行PHD预测和更新.

2.1 PHD-M滤波器

假设存活目标与新生目标的标签为β,状态矢量x中的动力学成分记为y,则x可用下式表示

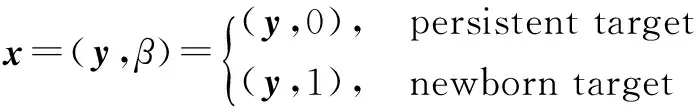
(1)

新生目标强度为

(2)

此时目标的状态转移密度fk|k-1(x|ζ)为

fk|k-1(x|x′)=fk|k-1)(y,β|y′,β))

(3)

则PHD-M滤波器预测方程为Dk|k-1(y,β)

(4)

对于存活目标(β=0),其更新方程为

Dk(y,0)=[1-pD,k(y)]Dk|k-1(y,0)

(5)

对于新生目标(β=1),其更新方程为

Dk(y,1)=

(6)

2.2 PHD-M的粒子实现

PHD-M滤波器将目标区分为存活目标和新生目标,在对PHD进行粒子实现时,需两组不同的粒子集进行近似,并分别进行预测和更新[16].

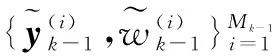
(7)

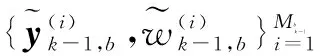
(8)

(9)

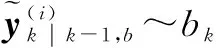
(10)

(11)

(12)

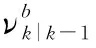
对于更新步,存活目标和新生目标可由式(13)和式(14)进行权值更新

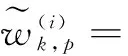
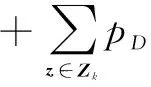
(13)

(14)

式中Λ(z)为归一化因子,其可用下式表示

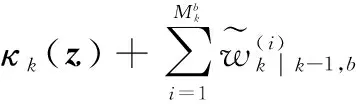
(15)

经预测步和更新步后,对粒子集进行重采样和聚类操作,即可提取多目标状态.

3 PHD-SM滤波器

PHD-SM滤波器采用基于单量测的PHD分解进行PHD更新,并通过构建一步虚拟量测对漏检目标进行补偿,因而能够更好的对漏检目标进行PHD表示.下面对PHD-SM滤波器进行介绍.

3.1 基于单个量测的PHD分解

考虑如下情形:在k时刻,若除了mk个量测外,传感器又接收到一个量测,研究此时PHD变化情况.假设原PHD为Dk(x),新PHD为ΞDk(x),则

Dk(x)=[1-pD,k(x)]Dk|k-1)(x)

(16)

ΞDk(x)=[1-pD,k(x)]Dk|k-1)(x)

(17)

新旧PHD之差为

ΔDk(x|zmk+1)=

(18)

ΔDk(x|zmk+1))反映了新增量测对多目标PHD的影响,其代表了新量测对应的目标(或杂波)的一阶后验密度.

综上,PHD可以进行如下分解

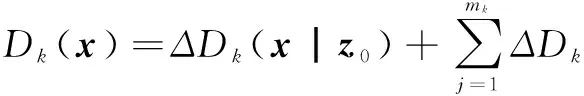
(19)

其中ΔDk(x|z0)=[1-pD,k(x)]Dk|k-1)(x)表示漏检目标的强度函数,ΔDk(x|zj))表示第j个量测的PHD.由此,任意时刻多目标PHD可表示为漏检目标的PHD与mk个量测对应的目标(或杂波)的PHD之和,式(19)即完成了基于单个量测的PHD分解.

3.2 一步虚拟量测的构建

当目标发生漏检时,PHD-M通过式(19)中的ΔDk(x|z0))对漏检目标进行PHD表示,然而在对滤波器实现时,由ΔDk(x|z0)很难实现精确的状态提取,考虑到目标运动的连续性,通过构建虚拟量测进行量测补偿,并替代ΔDk(x|z0)可解决这一问题.

假设k-1时刻目标估计集合可记为

(20)

k,e=Fk-1k-1,e

(21)

(22)

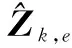
Zk,e=

(23)

(24)

若Zk,d=∅,表明所有转换量测均有实际量测与之对应,即认为此时不存在目标漏检.

3.3 PHD-SM滤波器

PHD-SM的预测方程与PHD-M相同,如式(4)所示.在PHD-SM的更新步,对于实际量测Zk,联合式(5)和式(19),可得存活目标(β=0)更新方程为

(25)

同理,对于一步虚拟量测Zk,d,可得存活目标更新方程为

(26)

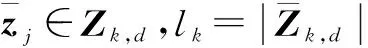
对于新生目标(β=1),联合式(6)和式(19),可得其更新方程为

(27)

4 PHD-SM滤波器的粒子实现

PHD-SM粒子滤波器通过构建一步虚拟量测对漏检目标进行补偿,同时采用粒子权值分解技术进行权值更新,在后续多目标状态提取时无须采用聚类方法,可有效降低因目标漏检所带来的估计误差并降低算法的复杂度.

4.1 粒子的权值分解

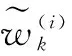
(28)

(29)

新旧权值之差为

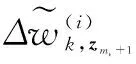
(30)

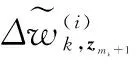
(31)

其中

(32)

(33)

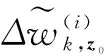
(34)

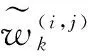
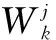
(35)

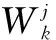
(36)

经基于样本和量测的权值分解,k时刻粒子权值Wk可以表示成如下形式

(37)

4.2 粒子的预测更新

预测步的粒子实现同PHD-M相同,可参见2.1节.在更新步,通过式(21)-(24)构建k时刻一步虚拟量测集Zk,d,在后续步骤中将Zk,d作为k时刻量测进行处理.

利用粒子权值分解技术进行权值更新,结合式(13)和式(31)可得存活目标的权值更新为

(38)

其中

(39)

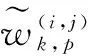
(40)

其中

(41)

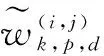
对于新生目标,仅由实际量测集Zk对权值进行更新,结合式(11)和式(19)可得

(42)

其中

(43)

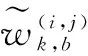
4.3 多目标状态提取

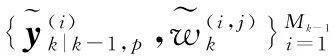
(44)

给定检验权值ξ1,若

(45)

则认定zj为目标量测,否则即为杂波量测.该量测对应的目标状态为

(46)

故由实际量测集对应的状态估计为

(47)

(48)

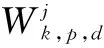
(49)

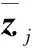
(50)

故由一步虚拟量测集对应的状态估计为

(51)

综合式(47)和式(51),得k时刻的状态估计为

k=k,e∪k,d

(52)

算法1k时刻PHD-SM滤波器流程

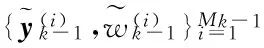
更新步:通过式(21)-式(24),构建一步虚拟量测集Zk,d

存活目标PHD更新:通过式(37)进行粒子权值分解

状态估计步:对于实际量测集Zk,通过式(47)计算k,e

对于一步虚拟量测集Zk,d,通过式(51)计算k,d

5 仿真验证

5.1 仿真设置

考虑2维目标做转弯运动的场景.假设多目标观测区域为[-250,250]×[-250,250]m2,目标存活概率为pS=0.95,不考虑目标衍生;传感器位于[0,0]T处,传感器观测时间为100步,传感器采样周期T=1s,仿真中粒子数目Lp=Lb=500,检测概率在仿真中给定.

(53)

(54)

(55)

仿真中取σ1,w=0.01m/s2,σ2,w=0.001rad/s2.则

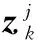
(56)

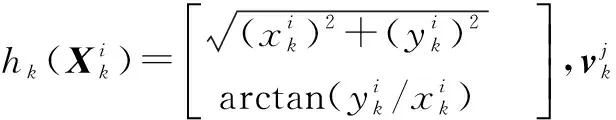
若杂波模型服从泊松点过程,其强度为

κk(z)=λc(zk)

(57)

除特殊说明外,仿真中取λ=10.

图1为目标真实运动航迹.目标1第2秒新生,第76秒消亡;目标2第14秒新生,第60秒消亡;目标3第40秒时新生,第100秒消亡;目标4第14秒新生,第60秒消亡.

5.2 仿真对比

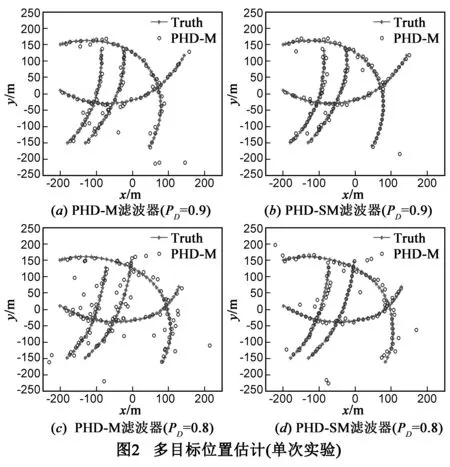
图2表示pD=0.9和pD=0.8时,PHD-M和PHD-SM滤波器的多目标位置估计.由图2(a)和图2(b)、图2(c)和图2(d)可知,在检测概率相同的情况下,PHD-M的漏估点个数明显多于PHD-SM,这是因为PHD-SM通过构建一步虚拟量测对漏检目标进行补偿,避免了聚类操作,从而能够对漏检目标进行有效地估计,减少虚假点估计个数;而对比图2(a)和图2(c)、图2(b)和图2(d)可知,随着检测概率的降低,两种滤波器估计性能均有所下降,但PHD-M性能下降更大,PHD-SM鲁棒性优于PHD-M,这是因为随着检测概率降低,漏检目标增加,PHD-M由于没有采用有效的漏检目标补偿方法,导致估计性能下降显著.

为评估PHD-M和PHD-SM的性能,采用OSPA距离来度量两者的跟踪误差,其定义参见文献[19].在仿真中参数设置为C=30和P=2.

图3表示pD=0.9和pD=0.8时,经50次MC实验两滤波器平均OSPA距离估计.由图3可得,PHD-SM估计精度优于PHD-M滤波器,其OSPA距离明显小于PHD-M.对比图3(a)和图3(b)可以看出,随着检测概率的降低,两种滤波器的跟踪性能均有所下降,但是PHD-M性能下降更为显著,即PHD-SM在低检测概率下跟踪性能相比PHD-M更有优势.同时,由图3还可以看出,在第14步和第40步,当目标数目向上突变时,两滤波器OSPA估计曲线均存在波峰,这是因为两种滤波器的个数估计是基于对存活目标粒子的权值和得到的,故新生目标的粒子必须经重采样成为存活目标粒子才可以被估计到,因此两滤波器具有估计滞后性.

为更直观地评价不同检测概率下两滤波器的性能,采用平均OSPA距离度量两者的估计误差,平均OSPA距离定义为

(58)

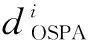
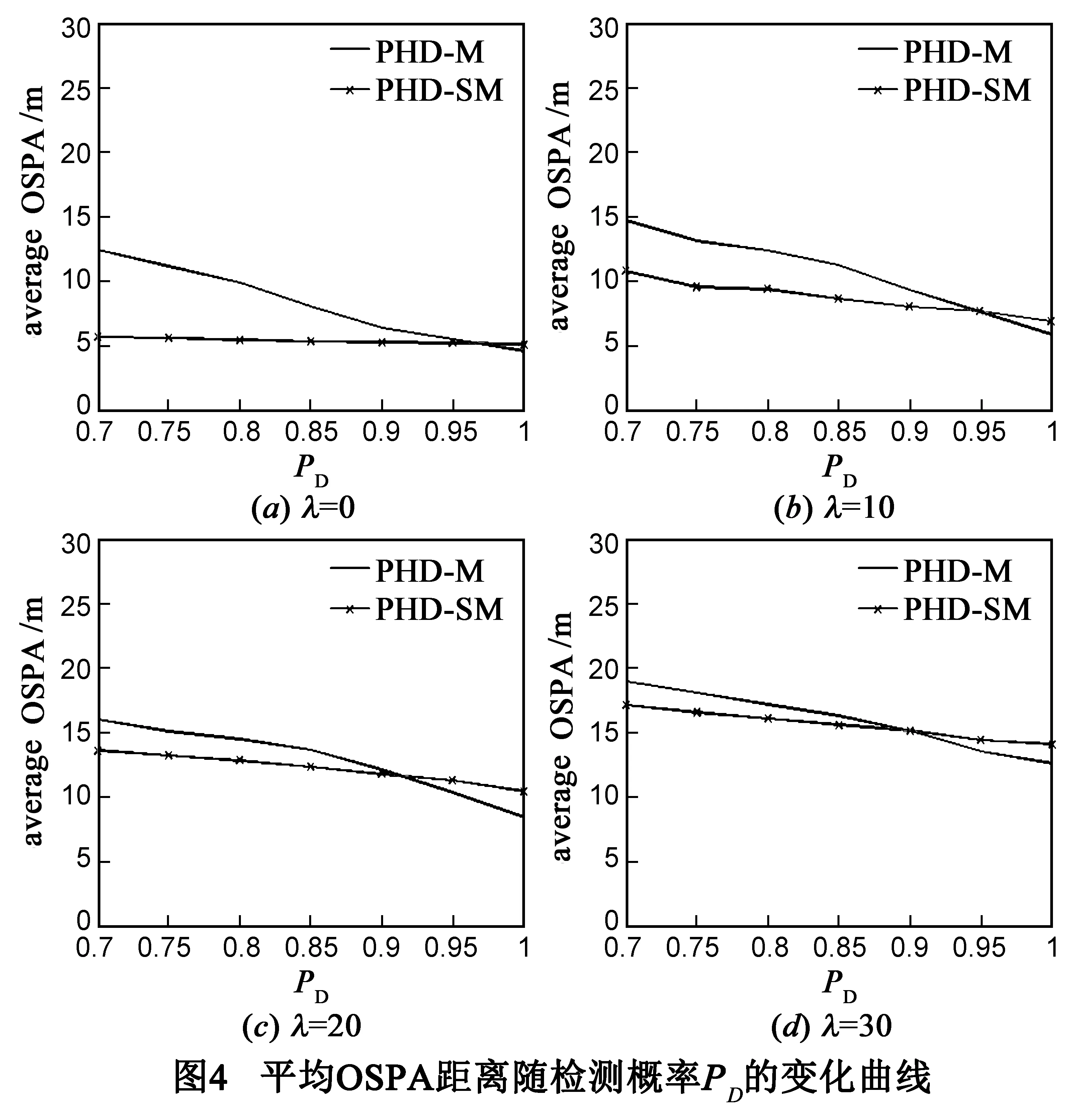
图4所示为不同杂波强度下两滤波器平均OSPA距离随检测概率PD的变化曲线.由图4(a)-(d)可知,随着PD的降低,两滤波器平均OSPA距离均有所下降,即估计性能均变差.当PD较小时,PHD-SM性能明显优于PHD-M,且PD越小,这种性能优势越明显,这是因为PHD-SM通过构建一步虚拟量测对漏检目标进行补偿,很好的避免了因目标漏检带来的性能损失.而当PD较大时,由于目标几乎不发生漏检,PHD-M性能要略优于PHD-SM.此外,对比图4(a)-(d)可知,随着λ的增大,两滤波器平均OSPA距离均有所下降,且平均OSPA距离曲线交点对应的PD值越来越小,这是因为当杂波强度较大时,PHD-SM通过一步虚拟量测对漏检目标进行补偿时,错将杂波估计为目标所致.

6 结论

当传感器检测概率较小时,由于存在漏检目标,将导致PHD-M滤波器估计性能下降.针对这一问题,本文通过构建一步虚拟量测对漏检目标进行补偿,并基于单量测PHD分解技术,提出了一种新生目标强度未知的单量测PHD滤波器PHD-SM,同时给出了一种无须聚类操作的多目标状态估计方法.仿真实验表明,相比PHD-M滤波器,PHD-SM滤波器能够有效估计漏检目标,且检测概率越小性能优势越明显.

[1]Bar-Shalom Y,Fortmann T E.Tracking and Data Association[M].Boston:Academic Press,1988.

[2]Bar-Shalom Y,Li X R.Multitarget-Multisensor Tracking:Principle and Techniques[M].Storrs,CT:YBS Publishing,1995.

[3]Fortmann T E,Bar-Shalom Y,Scheffe M.Sonar tracking of multiple targets using joint probabilistic data association[J].IEEE Journal of Oceanic Engineering,1983,8 (3):173-184.

[4]Blackman S S.Multiple hypothesis tracking for multiple target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,2004,19(1):5-18.

[5]Bar-Shalom Y,Fortman T E.Tracking and Data Association[M].San Diego:Academic,1988.5-40.

[6]何友,修建娟,关欣.雷达数据处理及应用(第三版)[M].北京:电子工业出版社,2013.1-10.

He Y,Xiu J J,Guan X.Radar Data Processing with Applications(Third Edition)[M].Beijing:Publishing House of Electronics Industry,2013.1-10.(in Chinese)

[7]Mahler R.Multitarget bayes filtering via first-order multitarget moments[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1152-1178.

[8]Vo B N,Ma W K.The Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Signal Processing,2006,54(11):4091-4104.

[9]Vo B N,Singh S,Doucet A.Sequential Monte Carlo methods for multitarget filtering with random finite sets[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1224-1245.

[10]Clark D,Vo B T,Vo B N.Gaussian particle implementations of probability hypothesis density filters[A].Proceedings of the 2007 IEEE Aerospace Conference[C].IEEE,2007.1-11.

[11]Ou Y C,Ji H B.Weight over-estimation problem in GMP-PHD filter[J].Electronics Letters,2011,47(2):139-141.

[12]Clark D,Ristic B,Vo B N,Vo B T.Bayesian multi-object filtering with amplitude feature likelihood for unknown object SNR[J].IEEE Transactions on Signal Processing,2010,58(1):26-37.

[13]王品,谢维信,刘宗香,李鹏飞.一种非线性GM-PHD 滤波新方法[J].电子学报,2012,40(8):1597-1602.

Wang P,Xie W X,Liu Z X,Li P F.A novel Gaussian mixture PHD filter for nonlinear models[J].Acta Electronica Sinica,2012,40(8):1597-1602.(in Chinese)

[14]Ma D,Fr D,Abreu G T.Adaptive gating for multitarget tracking with Gaussian mixture filters[J].IEEE Transactions on Signal Processing,2012,60(3):1533-1538.

[15]Ristic B,Clark D E,Vo B N.Improved SMC implementation of the PHD filter[A].Proceedings of the 13th International Conference on Information Fusion[C].Edinburgh,2010.1-8.

[16]Ristic B,Clark D E,Vo B N.Adaptive target birth intensity for PHD and CPHD filters[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(2):1656-1668.

[17]欧阳成,华云,高尚伟.改进的自适应新生目标强度PHD滤波[J].系统工程与电子技术,2013,35(12):2452-2458.

Ou Y C,Hua Y,Gao S W.Improved adaptive target birth intensity for PHD filter[J].Systems Engineering and Electronics,2013,35(12):2452-2458.(in Chinese)

[18]Mullane J,Vo B N,Adams M,Vo B T.A random finite set approach to Bayesian SLAM[J].IEEE Transactions on Robotics,2011,27(2):268-282.

[19]Schu D,Vo B T,Vo B N.A consistent metric for performance evaluation of multi-object filters[J].IEEE Transactions on Signal Processing,2008,56(8):3447-3457.

徐从安 男,1987年生于山东日照.海军航空工程学院信息融合研究所博士.研究方向为随机集多目标跟踪理论、数据处理.

E-mail:xcatougao@163.com

熊 伟 男,1976年生于江西.海军航空工程学院信息融合研究所教授,硕士生导师.研究方向为多源信息融合、系统仿真、态势估计与评估等.

刘 瑜 男,1986年生于湖南邵阳.海军航空工程学院信息融合研究所讲师.研究方向为多源信息融合、分布式状态估计等.

何 友 男,1956年生于吉林磐石.中国工程院院士,海军航空工程学院信息融合研究所教授,博士生导师.研究方向为多源信息融合、雷达自适应检测、系统仿真与作战模拟等.

A Single Measurement PHD Filter with Unknown Target Birth Intensity

XU Cong-an,XIONG Wei,LIU Yu,HE You

(ResearchInstituteofInformationFusion,NavalAeronauticalandAstronauticalUniversity,Yantai,Shandong264001,China)

In situations where the targets cannot be detected in the surveillance region,the estimated performance of the adaptive target birth intensity probability hypothesis density (PHD) filter will get worse because of false or low estimate.To overcome this problem,with unknown target birth intensity,a single measurement PHD (PHD-SM) filter and its sequential Monte Carlo (SMC) method are proposed.First,the undetected targets are compensated through developing the one step virtual measurement set.Afterward,according to the single measurement decomposition technique of PHD,the predication and update equations are derived.Finally,a novel multi-target state estimation method is presented.The simulation results show that,when the detection probability PDis small,PHD-SM filter has higher estimation performance.Moreover,the smaller the detection probability,the more significant advantage of estimation performance for PHD-SM filter.

multi-target tracking;probability hypothesis density;unknown target birth intensity;single measurement;one step virtual measurement

2015-03-26;

2015-11-01;责任编辑：李勇锋

TN957;TP391

A

0372-2112 (2016)10-2300-08

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.003