多波信号到达时间自动识别的核函数方法研究

任 波，宋瑞雪，付志伟

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)



多波信号到达时间自动识别的核函数方法研究

任 波，宋瑞雪，付志伟

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

信号所到达时间的具体信息，对于信号发射事件的定位，识别和信号发射源机理的分析都十分重要。提出了一种基于核函数的自动识别算法，该算法利用噪声信号和发射信号的核函数模型，利用Akaike的信息准则，对信号到达的时间进行了自动识别。该方法较其他方法具有计算简便的优点。仿真试验结果表明，基于核函数模型的信号到达时间识别的算法运行速度快，可以实时对信号的到达时间进行识别，能够给出较为准确的结果。

模型；核函数；到达时间；自动识别

在多项科学实验中，信号到达时间的自动识别普遍用来检测、定位和估计信号发射源的各项特性，并取得了很好的效果。

地震波指的是从震源产生的弹性波，该波从震源向四周辐射，当地震时，震源周围的介质发生急速的破裂，伴随着强烈的运动，这种运动就构成了一个波源。在地震波的研究中，地震波信号到达时间的确定对于震源的定位、识别以及地震波的特性和传播特征的分析都非常有意义。

在Akaike信息准则基础上，利用回归(AR)模型的定阶和选择可以识别信号到达时间[1]。本文分别利用AR模型和核函数模型对实验的地震波进行到达时间的自动识别，结果表明基于核函数模型的识别效果明显优于基于回归(AR)模型的识别效果。

1 信号到达时间的自动识别方法

AIC准则是在1973年由Akaike从信息论的角度提出的，Akaike将这个准则应用于回归(AR)模型的定阶和选择中，获得了比较理想的效果[1-2]。该方法的理论思想为：一个时间序列能够被分割成局部稳定的时段，自回归模型能够拟合每一个时段。基于AR模型的AIC算法[3]应用了这个思想。将仿真实验得到的数据分为两个局部稳定的时间序列，每一个时间序列都用自回归过程来模拟，之后寻找一个最佳分割点，该分割点将波形数据分为两个稳定的不同时间序列，信号的到达时间就是这个最佳分割点，如图1所示。

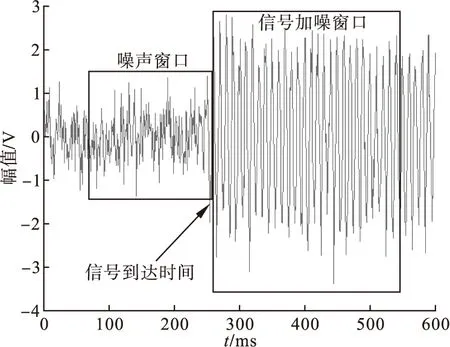
图1 信号到达波形图

xn={x1,…,xn}为实验数据的时间序列，若该实验数据包含信号到达时间，则信号到达时间将这段时间序列分成了两个时段：信号到达前的时段i(i=1)和信号到达后的时段i(i=2)。分别对时段i(i=1)和时段i(i=2)用数据xt自回归模型来模拟。

(1)

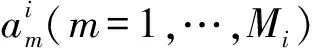
(2)

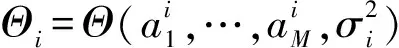
pi=M1+1，p2=K+1，q1=K，q2=N-M2，n1=K-M1，n2=N-M2-K

为便于运算，应用极大似然方法，取式(2)的对数并对其求偏导数，找到模型参数的极大似然估计，可得下式：

(3)

对式(3)进行求解，可以得到模型参数：

(4)

因此，以对数似然函数的最大值作为K的函数，可得

log(L(x,K,M1,M2,Θ1,Θ2))=

(5)

可得

(M1+M2)(log2π+1)-N(log2π+1)

定义关于K的AIC函数为

AIC(K)=-2log(L(x,K,M1,M2,Θ1,Θ2))

如果噪声AR模型的阶数M1和信号加噪声AR模型的阶数M2为定值，则AIC函数可如下表示：

(6)

式中C=(M1+M2-N)(log2π+1)为常数。

当K为信号到达时间即位于噪声窗口和噪声加信号窗口的分割点时，K之前的时间序列[M1+1,K]全部都是噪声，K之后的时间序列[K+1,N-M2]全部都是信号加噪声，从而噪声AR模型和信号加噪声的AR模型都能进行最佳模拟，因此K点前后预测误差的方差都能够取得最小值使得AIC(K)的值最小，由此说明噪声窗口和噪声加信号窗口的最佳分割点即信号到达时间为AIC函数取得最小值的点。

应该要说明一点的是，AIC函数的最小值为信号到达时间，因此使用AIC方法识别时，需要在信号到达时刻附近定义合适的时间窗口。与此同时，AIC的方法还要对前后的窗口进行建模。

由上述的说明不难看出，基于AR模型的算法是一种线性的方法，在线性邻域能够取得理想的效果，而地震波的分布通常是非线性的，因此需要一种非线性的方法来探寻地震波的到达时间。

2 基于核函数的建模

2.1 核函数简介

核方法把先前只限于线性系统的方法的理论性和非线性方法的灵活性与适用性相结合，从而形成了一类非常强有力的、健壮的模式分析技术。

在模式分析的研究中，要使得模式识别更容易，可以给数据重新进行编码。用核方法进行模式分析就是这样一个方法。核方法的步骤如下：首先把数据嵌入到合适的特征空间，再使用基于线性代数，几何学和统计学的方法，发现嵌入数据中的模式[5]。

核方法的解决方案分两个部分：一个模块和一个学习算法。模块执行的是从原始数据映射到嵌入空间(或特征空间)的过程，学习算法则是用来发现这一空间的线性模式。在本文中，模块是用核函数将噪声数据和信号加噪声数据映射到嵌入空间，而学习算法是利用核函数的模型来执行AIC函数。

在实际应用中，核函数所需的计算量显著小于显示计算对应数据特征的计算量。

2.2 高斯核

目前存在多种核函数，使用最广泛的核为高斯核。对于σ>0，高斯核(Gaussiankernel)由下式定义：

(7)

对于高斯核来讲，由于所有映射后的点的内积都为正，κ(x,z)=exp(0)=1。所有点的映像在特征空间中的范数都是1。

2.3 基于高斯核的建模及信号到达时间的识别

与AR-AIC方法原理相同，基于核函数的信号到达时间自动识别也需要先在信号到达时刻附近定义合适的窗口，对噪声窗口和信号加噪声窗口进行建模，不同的是建模的过程应用的是高斯核函数。

与AR-AIC方法类似，先选定包含信号到达时间的实验数据的时间序列xn={x1,…,xn}，选定噪声模型的阶数M1和信号加噪声的阶数M2进行建模。

与AR的自回归建模不同的是，在选定的时间序列中，求时间序列的前M1(定义为噪声模型的维数)个数据的高斯核函数矩阵GM1作为噪声模型，然后选定的时间序列的最后M2(即N-M2+1至第N个)(定义为信号加噪声模型的维数)个数据的高斯核函数矩阵GM2作为信号加噪声的模型。

(8)

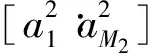
(9)

与式(2)至式(6)的推导方法相同，也是运用极大似然法，可推出基于高斯核矩阵模型的AIC函数可表示为

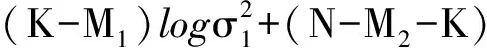
(10)

与式(6)相同，当K为信号到达时间即位于噪声窗口和噪声加信号窗口的分割点时，K之前的时间序列[M1+1,K]全部都是噪声，K之后的时间序列[K+1,N-M2]全部都是信号加噪声，从而噪声AR模型和信号加噪声的AR模型都能进行最佳模拟，使得K点前后预测误差的方差都能够取得最小值，由此说明噪声窗口和噪声加信号窗口的最佳分割点即信号到达时间为AIC函数取得最小值的点。

原理同AR-AIC方法，使得AIC(K)取得最小值得K值即为信号到达时间。

以上可以总结出基于核函数模型的信号到达时间自动识别的步骤：

(1)选择合适的窗口，即该窗口包含信号到达时间；

(2)定义合适的M1值和M2值；

(3)根据式(9)计算AIC(K)值，最小值即为信号到达时间。

3 仿真实验结果

3.1 软件仿真效果

假设窗口的噪声为高斯白噪声，信号为标准正弦信号，振幅为2，频率为200Hz；如图2所示，信号在250s时到达；令M1=M2=100，带入式(10)中，可以得到识别的结果如图3所示。

3.2 多波到达时间的自动识别

如图4所示，有两处信号到达，令t=500ms和t=1200ms时信号到达，先选定第一次信号到达时间包含于[200∶700]内，在此区间内用基于高斯核的到达时间自动识别；再选定第二次信号到达时间包含于[1100∶1300]内，同样用该方法，噪声阶数和噪声加信号阶数同样为M1=M2=100；可以得到识别效果图3、图5，分别在t=500ms和t=1200ms处取得了局部最小值，识别效果较为理想。

图2 窗口时间序列

图3 基于高斯核的AIC方法识别结果

图4 多波到达窗口

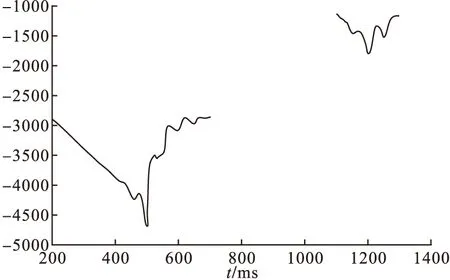
图5 多波到达时间识别效果图

3.3 在实际信号中的应用

AIC方法在实际应用中取得了理想的效果，以下是一个地震波的例子，时间序列如图6所示。

图6 地震波时间序列图

可见信号大约在2700～2800ms处到达，因此将时间序列选为[2600∶3000]；令M1=M2=100，利用基于AR模型的信号到达时间识别方法，效果如图7所示。

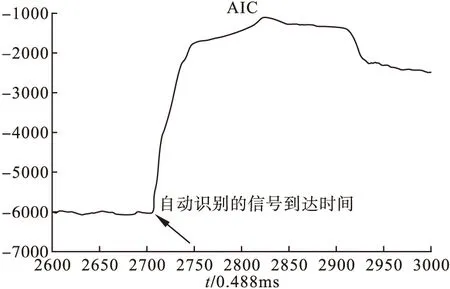
图7 基于AR模型识别方法效果图

由图7可见，在地震波的到达时间的识别上，基于AR模型的效果并不是特别理想。而在基于核函数模型的识别方法的过程中，噪声的高斯核函数模型与被识别序列的高斯核函数模型的方差如图8所示。

图8 噪声高斯核函数模型的方差

噪声加信号的高斯核函数模型与被识别序列的方差如图9所示。

图9 噪声加信号高斯核函数模型的方差

利用基于核函数模型的识别方法的结果如图10所示。

图10 基于核函数的识别效果

由图10可见，基于核函数的方法取得了较为理想的效果，AIC曲线在地震波信号到达处取得了最小值，且两种方法识别的信号到达时间几乎一致。而基于AR模型的识别方法没有在信号到达处取得最小值，只是能够再将AIC函数对时间t进行求导，找出一阶导数不存在的点即为地震波的到达时间；但在运行的过程中，基于核函数模型的识别方法所需时间明显少于基于AR模型的识别方法所需时间，计算的步骤也更为简便。

4 结束语

基于核函数的AIC方法利用核函数的原理，属于非线性的方法，在地震波到达时间的识别上较AR-AIC方法计算简便，效果较理想，当噪声较大时，先采用合适的方法进行滤波再进行识别也能够取得较为理想的识别效果，对于多波的到达时间的自动识别也较为准确。

[1]Akaike H.Markovian representation of stochastic proce-sses and its application to the analysis of autoregressive moving average process[J].Annals of the Institute of Statistical Mathematics,1974,26(1):363-387.

[2]Kitagawa G,Akaike H.A procedure for the modeling of nonstationary time series[J].Annals of the Institute of Statistical Mathematics,1978,30(1):351-363.

[3]王晓伟,刘占生,窦唯.基于AR模型的声发射信号到达时间自动识别[J].振动与冲击,2009,28(11):79-83.

[4]王鲁平,张路平,韩建涛.采用灰度加权核函数的动态背景运动目标检测算法[J].红外与激光工程,2013(12):3453-3457.

[5]Shawe Taylor J,Cristianini N.Kernel methods for pattern analysis[J].Kernel Methods for Pattern Analysis,2004,101(2):77-78.

(责任编辑：马金发)

Research on Automatic Recognition of the Arrival Time of Multiwave Signal Model Based on Kernel Function

REN Bo,SONG Ruixue,FU Zhiwei

(Shenyang Ligong University,Shenyang 110159,China)

Signal arrival time information is very important for the localization，identification of signal emission event and the analysis of mechanism of signal emission source.A new algorithm for automatic recognition based on kernel function is presented.The algorithm uses the kernel function model of the noise and the transmitted signal.By Akaike criterion application,the signal arrival time is automatically recognized.This method has the advantages of simple calculation in comparison with other methods.Simulation results show that the signal arrival time algorithm based on kernel function model runs fast.It could identify the arrival time of the real-time signal and give more accurate results.

model;kernel function;arrival;automatic recognition

2015-07-13

任波(1962—)，男，教授，研究方向：导航、制导与控制。

1003-1251(2016)04-0027-06

TP391

A