共点又等长 旋转来变换

□ 周奕生

共点又等长 旋转来变换

□ 周奕生

旋转变换是几何图形三大变换之一，当图形中出现我们所关注的某个三角形的某条边与其他边具有“共点等长且夹角为特殊角（比如60°、90°等）”时，一般可采用旋转变换，将该三角形绕着“共点”的点旋转，使得“等长”的边重合.我们这样利用旋转变换可以解决许多具有一定难度的几何问题.

例1 如图1，已知P是等边△A B C 内 一 点 ，∠A P B＝140°，∠A P C＝130°，求以P A、P B、P C为三边的三角形的各个内角的度数.

图1

解析：求解的关键是构造以P A、P B、P C为三边的三角形，而构造的关键是对P A、P B、P C的位置进行变换.注意到B A＝B C，∠A B C＝ 60°，故考虑将△BA P绕点B旋转60°得△B C Q，此时P A＝Q C，P B＝Q B，这相当于把P A、P B分别变换到Q C、Q B.易知△B P Q是等边三角形，从而Q B＝P Q，这样以P A、P B、P C为边的三角形就是△P Q C.在△P Q C中，∠PQ C＝∠BQ C－60°＝140°－60°＝80°，∠Q PC＝∠B P Q－60°＝（360°－140°－130°）－60°＝30°，∠PC Q＝180°－80°－30°＝70°.

例2 如图2，P、Q是等腰Rt△A B C斜边A B上两点，且∠P C Q＝45°，试判断以A P、P Q、B Q三条线段长为边能否构成三角形？如果能，请说明这个三角形的形状；如果不能，请说明理由.

图2

解析：欲判断以A P、P Q、B Q三条线段能否构成三角形，由于它的长不确定，所以应通过变换将它们集中到同一个三角形中去，再作比较.由于C A＝C B，且它的夹角为90°，因此可把△A C P绕点C顺时针旋转90°得△B C P′，连接P′Q，则C P′＝C P，∠B C P′＝∠A C P，AP＝B P′，∠C B P′＝∠A＝45°，从而∠P′B Q＝90°.下面只须再探索P′Q是否等于P Q？

由 ∠P C Q＝45°，得 ∠A C P＋∠B C Q＝45°，所以∠P′C Q＝45°＝∠P C Q，所以△P′C Q≌△P C Q，所以P′Q＝P Q.

因此，以A P、P Q、B Q三条线段长可构成与Rt△P′B Q一样的直角三角形.

例3 已知点P是正方形A B C D内一点，连接P A、P B、P C.

（1）若 P A＝2，P B＝4，∠A P B＝135°，求P C的长；

（2）若P A2＋P C2＝2P B2，请说明点P必在对角线A C上.

解析：（1）将P A、P B变换到与P C在同一个三角形中.由于△P A B的边B A与B C“共点等长”，所以将△P A B绕点B顺时针旋转90°得△P′B C，连接 P P′（图 3①），则△B P P′是等腰直角三角形，所以∠B P′P＝45°，P P′＝ 2 B P＝4 2.

又∠B P′C＝∠A P B＝135°，所以∠P P′C＝90°，

（2）欲证点P在A C上，只须证∠A P B＋∠B P C＝180°.将△A B P绕点B顺时针旋转90°得△C B P′，则∠A P B＝∠C P′B，因此只须证∠C P′B＋∠B P C＝180°.连接P P′（如图3②），则在等腰直角三角形P P′B中，P P′2＝2 P B2，再由已知P A2＋P C2＝2 P B2及P′C＝P A，得P P′2＝P A′＋P′C2，根据勾股定理逆定理，知∠P C P′＝90°，所以∠C P′B＋∠B P C＝360°－2× 90°＝180°，故A、P、C三点共线，即点P在A C上.

图3①

图3②

例4（武汉）如图4，在四边形A B C D中，A D＝4，C D＝3，∠A B C＝∠A C B＝∠A D C＝45°，则B D的长为______.

分析：由于B D所在的△A B D除了已知边A D＝4外，并无其他特殊性，而由∠A B C＝∠A C B＝45°，得∠B A C＝90°，A C＝A B，故将△A B D绕点A顺时针旋转90°得△A C E，则

B D＝C E，A D＝A E，∠D A E＝90°，所以∠AD E＝45°.又∠A D C＝45°，所以∠C D E＝90°.由A D＝4，得D E＝，又C D＝3，所以C E＝＝此即B D的长.

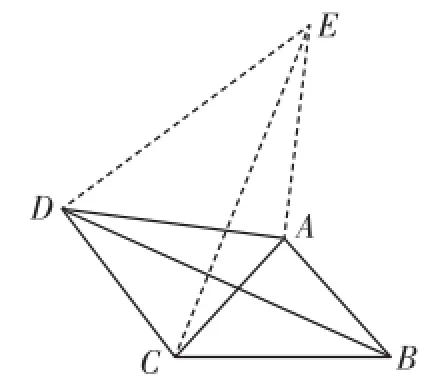
图4

例5 如图5，点P为正方形A B C D内一点，且∠A P D＝90°，点P到点A及正方形的中心O的距离分别为P A＝4，P O＝求P D的长.

图5

解析：由O为正方形A B C D的中心，所以△A P O的边O A等于O B，又O A和O B的夹角为90°，故把△A P O绕点O逆时针旋转90°得△B P′O，连接P P′，则△O P P′为等腰直角三角形，所以∠O P P′＝∠O P′P＝45°.因为P O＝6 2，所以P P′＝12.因为∠A P D＝∠A O D＝90°，则A、D、O、P四点共圆，所以∠O P D＝∠O A D＝45°，所以∠A P P′＝180°，A、P、P′三点共线，所以A P′＝A P＋P P′＝16.又∠P′B O＝∠PA O，所以∠A B P′＋∠B A P′＝∠A B O＋∠B A O＝90°，则∠A P′B＝∠A P D＝90°.又B P′＝A P，AB＝A D，所以△A B P′≌△D A P，所以P D＝P′A＝16.

例6（咸宁）如图6①，正方形O A B C的边O A、O C在坐标轴上，点B的坐标为（－4，4）.点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动.连接B P，过P点作B P的垂线，与过点Q平行于y轴的直线l相交于点D.B D与y轴交于点E，连接P E.设点P运动的时间为t（s）.

图6①

（1）∠P BD的度数为_____，点D的坐标为_____（用t表示）；

（2）当t为何值时，△P B E为等腰三角形？

（3）探索△P O E周长是否随时间t的变化而变化，若变化，说明理由；若不变，试求这个定值.

解析：（1）欲求∠P B D的度数，由已知∠B P D＝90°，可判定P B是否等于P D来解决？从点P、Q的运动情况可知A P＝O Q，所以P Q＝O A.又四边形O A B C是正方形，所以O A＝A B，所以P Q＝A B.因为BP⊥P D，所以∠A P B＋∠D P Q＝90°.又∠A P B＋∠A B P＝90，所以∠A B P＝∠D P Q.因为l⊥x轴，∠P Q D＝90°＝∠B A P.所以△P A B≌△D Q P，P B＝P D.所以∠P B D＝45°.

欲求点D的坐标，需要知道Q O及D Q的长.由于Q O＝P A＝t，所以点D的横坐标为x＝t.因为△P A B≌△D Q P，所以D Q＝A P＝t，点D的纵坐标为y＝t.故点D的坐标为（t，t）.

（2）欲使△P B E为等腰三角形，由于没有具体指定腰或底边，所以需要对腰或底边进行分类讨论.但注意到由△P A B≌△D Q P得P B＝P D，所以显然有P B≠P E，即等腰△P B E的底边不能是B E.

下面分两种情况讨论求解：

（Ⅰ）若P B为底边，即E B＝E P，则∠E P B＝∠E B P＝45°，此时点P与O点重合，t＝4；

（Ⅱ）若P E为底边，即B E＝B P，则由“HL”得△P A B≌△E C B，

∴ C E＝P A＝t.

过D点作D F⊥O C于点F（如图6②），

则D F＝O F＝t，E F＝4－2 t.

∵ △B C E∽△D F E，

△P B E为等腰三角形.

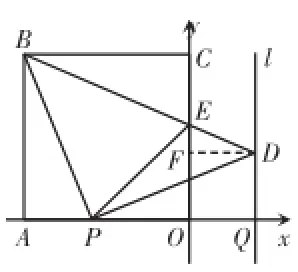
图6②

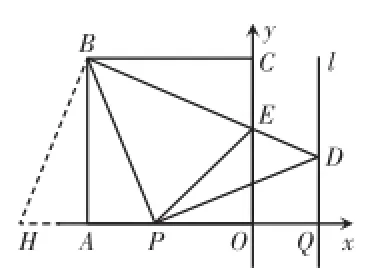
图6③

（3）欲知△P O E周长是否随时间t的变化而变化？需考虑△P O E三边的和.由于△B C E的边B C与B A共点等长，且夹角为90°，故对△B CE进行旋转变换，即将△B C E绕点B按顺时针方向旋转90°，得到△B A H（如图6③），则B E＝B H，C E＝A H，∠E B H＝90°，

∴ ∠EB P＝45°＝∠P B H，

又B P＝B P，

∴ △P B E≌△P B H，

∴ E P＝P H＝A H＋A P＝C E＋A P.

∴ △P O E的周长＝O P＋O E＋P E＝O P＋O E＋C E＋AP＝O A＋O C＝4＋4＝8.

所以，△P O E周长不随时间t的变化而变化，其值总是8.