值得关注的转化技巧——构造辅助圆

□邹新

值得关注的转化技巧
——构造辅助圆

□邹新

以人教版为例，教材中关于点共圆的相关知识主要有三个：一是“到定点的距离等于定长的点都在同一个圆上”；二是“三点共圆”，三角形外接圆及直角三角形的外接圆圆心是斜边中点（教材习题）；三是“四点共圆”的一个基本性质为圆内接四边形的对角互补.下面举例说明解题时根据上述知识要点构造辅助圆，进行转化.

一、到定点的距离等于定长时可作辅助圆

例1（自贡）如图1，在矩形A B C D中，A B＝4，A D＝6，E是A B边的中点，F是线段B C边上的动点，将△E B F沿E F所在直线折叠得到△E B′F，连接B′D，则B′D的最小值是（ ）.

图1

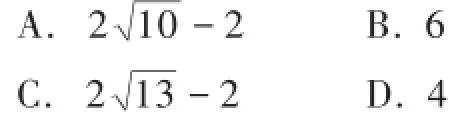
解析：E为A B的中点，点F在B C上，沿EF对折，则E B的对应线段E B′＝E B＝为定值，故B、B′在以E圆心、E B为半径的上（不含点A），如图2，设D E交于点M.当点B′与点M重合时B′D最小，如图3，此时D B′＝D E－E B′＝2 10－2.选A.

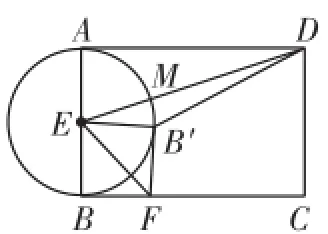
图2

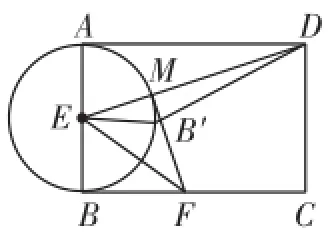
图3

例2（梅州）在Rt△A B C中，∠C A B＝90°，A C＝A B＝4，D、E分别是A B、A C的中点.若等腰Rt△AD E绕点A逆时针旋转，得到等腰Rt△A D′E′，如图4.设旋转角为α

（0＜α≤180°），记直线B D′与C E′的交点为P.点P到A B所在直线的距离的最大为____.

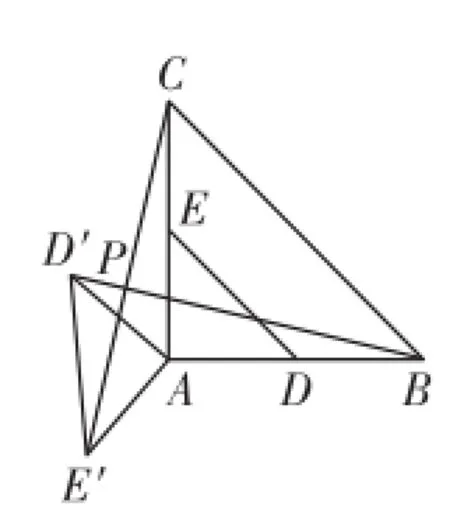
图4

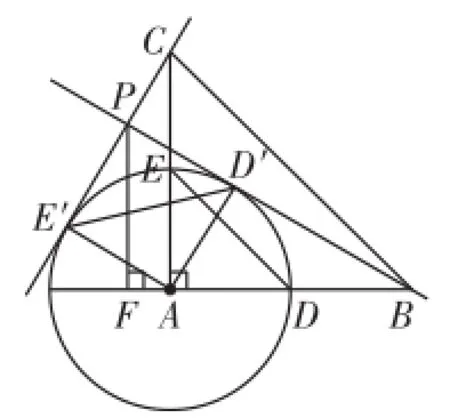
图5

解析：如图5，作P F⊥AB，垂足为点F.

易证△C E′A≌△B D′A，

∴ ∠E′C A＝∠D′B A，

进而易证B P⊥C P.

已知等腰Rt△A D E绕点A逆时针旋转，得到等腰Rt△A D′E′，

∴ D′、E′在以A为圆心、A D为半径的圆上，

∴ 当B D′所在直线与⊙A相切时，直线B D′与C E′的交点P到直线A B的距离最大.

此时易证四边形A D′PE′是正方形，∴ P D′＝AD′＝A D＝2.

在Rt△A B D′中，

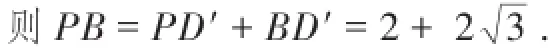
又在Rt△A B D′中，

故∠A B P＝30°，

二、当两个直角三角形有公共斜边时可作辅助圆

例3（北京）如图6，正方形A B C D的中心为O，面积为1989，P为正方形内的一点，且∠A P B＝90°，P A∶ P B＝5∶14，求P B的长及∠O P B的大小.

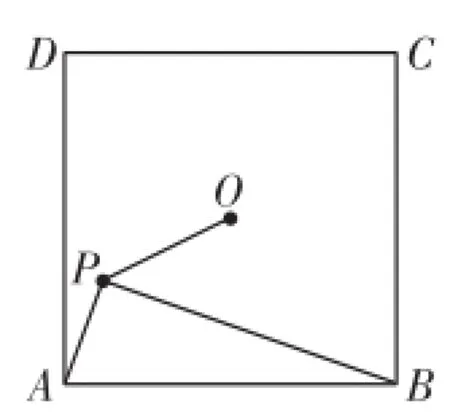
图6

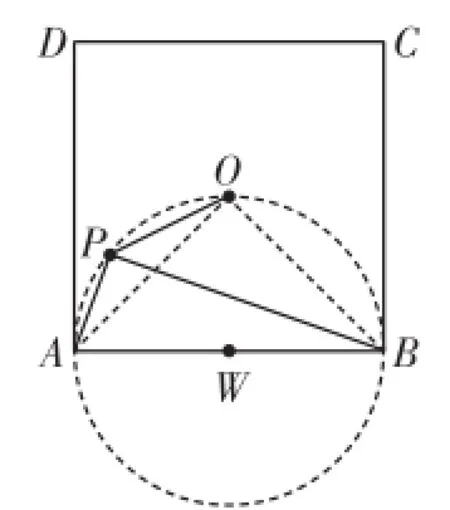
图7

解析：在Rt△A P B中，设P A＝5 x，P B＝14 x，根据勾股定理，

得（5 x）2＋（14 x）2＝1989，

解得x＝±3（负值舍去），

所以P B＝42.

连接O A、O B.由正方形性质可知，∠A O B＝90°＝∠A P B，

由于Rt△A B P与Rt△A B O的外接圆直径为公共斜边A B，所以A、B、O、P四点共圆，如图7.

又点O为正方形A B C D的中心，

∴ ∠O A B＝45°，

所以∠O P B＝∠O A B＝45°.

例4 如图8，E是正方形A B C D的边A B上的一点，过点E作D E的垂线交∠A B C的外角平分线于点F.求证：F E＝D E.

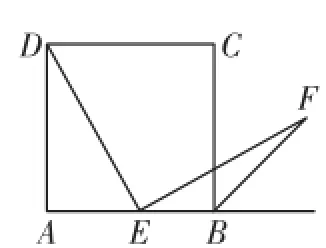
图8

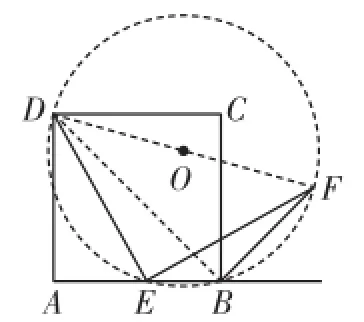
图9

解析：连接D B、D F，如图9.

因为B F是∠A B C的外角平分线，∠A B C＝90°，

∴ ∠C B F＝45°，

由正方形的性质可知，∠D B C＝∠D B E＝45°，所以∠D B F＝90°.

又已知∠D E F＝90°，

所以△D B F与△D E F有公共外接圆，其外接圆直径为D F，

∴ ∠D F E＝∠D B E＝45°.

又D E⊥E F，所以△D E F为等腰直角三角形，∴ F E＝D E.

三、作三角形的外接圆实施角的转化

例5 如图10，△A B C中，B F、C E交于点D，B D＝C D，∠B D E＝∠A，求证：B E＝C F.

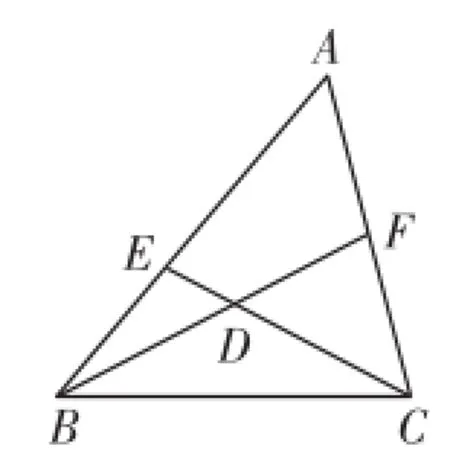
图1 0

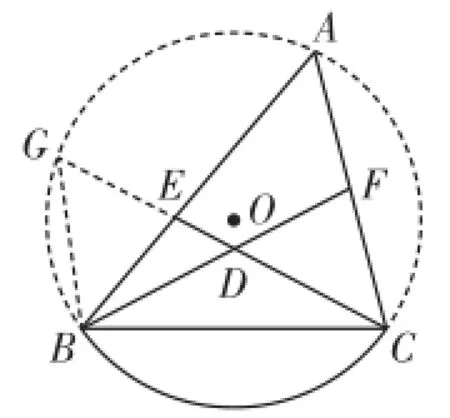
图11

解析：作△A B C的外接⊙O，延长C E交⊙O于G，连接B G，如图11.

∵ ∠G＝∠A，∠B D E＝∠A，

∴ ∠G＝∠B D E，∴ B G＝B D.

又B D＝C D，所以B G＝CD.

又∵ ∠G＝∠C D F，

∠G B E＝∠D C F，

∴ △G B E≌△D C F.

∴ B E＝C F.

例6 如图12，P、Q为线段B C上两定点且B P＝C Q，A为B C外一动点，当点A运动到使∠B A P＝∠C A Q时，求证：△A B C为等腰三角形.

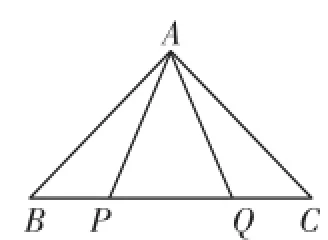
图12

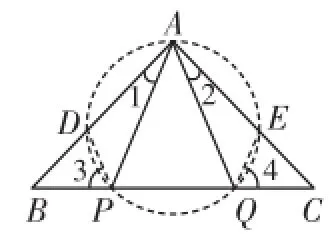
图13

解析：作△A P Q的外接圆交AB于点D，交A C于点E，如图13.

∵ ∠B A P＝∠C A Q，

可证D P＝Q E.

又A、D、P、Q四点共圆，

∴ ∠3＋∠D P Q

＝∠D P Q＋∠D A Q＝180○，

∴ ∠3＝∠D A Q.

同理∠4＝∠E A P.

又∠1＋∠P A Q＝∠D A Q，

∠2＋∠P A Q＝∠P A E，

且∠1＝∠2，∴ ∠D A Q＝∠E A P，

∴ ∠3＝∠4.

在△B P D与△C Q E中，

D P＝E Q，∠3＝∠4，B P＝C Q，

∴ △B P D≌△C Q E，∠B＝∠C.

即△A B C为等腰三角形.

通过上述题目的解答，我们确实可以看出运用辅助圆解题的巧妙，且有简洁美与奇异美，希望同学们在数学学习的过程中细心体会，灵活思考，巧妙应用.