潜水回水初始阶段的定性半定量分析及对水跃成因的解释
2016-12-07孙宝亮梁俊红崔卫利吴义松马广智
孙宝亮,梁俊红,崔卫利,吴义松,马广智
(1.东北大学资源与土木工程学院,沈阳 110004; 2.中南冶金地质研究所,湖北 宜昌 310014;3.中冶北方工程技术有限公司,辽宁 大连 116600)
孙宝亮1,梁俊红1,崔卫利1,吴义松2,马广智3
(1.东北大学资源与土木工程学院,沈阳 110004; 2.中南冶金地质研究所,湖北 宜昌 310014;3.中冶北方工程技术有限公司,辽宁 大连 116600)
文章提出并采用水力坡度分析方法,对潜水回水初始阶段进行了定性-半定量分析,为了解潜水回水过程提供了新的视角。通过分析潜水回水初始时刻的水力坡度,河渠侧的界面被分为2段:河间潜水位之上的铅直段和之下的水平段。水平段上点的水力坡度最大且相等,方向为水平向右;铅直段上点的水力坡度方向趋于铅直向下,越向上水力坡度越小。经过微小时间段Δt后,水力坡度均相应变小,铅直段相邻点间地下水运动发生冲突,水力坡度方向由趋于铅直向下向右偏转。将水力坡度分析方法用于分析潜水井流的过程和特征,水跃的成因可解释为:在相同水力坡度和过水断面面积下,井内大空间水流速度远大于孔隙中的潜水流速度,井内水位急速下降,从而形成水跃;水跃越大,进入井内的流量就越大。
潜水;回水;水力坡度;定性分析;井;水跃(渗出面)
0 引言
现有大多数地下水动力学教材中,潜水回水非稳定运动数学模型基于布西涅斯克方程建立,之后线性化布西涅斯克方程,再用有限傅里叶正弦变换得到该模型的级数解析解[1-5]。问题在于,布西涅斯克方程应用的是裘布依假设,而实际上在河附近的垂直流动分量大且不可忽视,裘布依假设并不成立[6-7]。河水位在大幅度变动的情况下,潜水厚度(M)不能代表真实水位高度,导水系数(T=KM)与实际不符,因而线性化的布西涅斯克方程解的误差较大[7-8]。鉴于此,本文提出利用水头和水力坡度分析方法,对潜水回水初始阶段非稳定运动进行定性-半定量分析;由于潜水井流与潜水回水初始阶段有相似之处,可将水力坡度分析方法用于分析描述潜水井流,有助于深入了解潜水井流的过程和特征,获得较为准确的流网,从而解释水跃产生的原因。水头和水力坡度分析方法为了解潜水回水过程及理解不同层位潜水运动的状态和特征提供了新的视角。
1 潜水回水的物理模型
河水面的抬高、河渠地表水的侧渗作用来补充地下水,会引起潜水位相应抬高,称为潜水回水[5]。其物理模型为:含水层均质各向同性,隔水底板水平;初始状态左河渠与河间潜水有相同水位h2;左河渠水位汛时上升为定值h1,发生瞬时回水,河渠间潜水非稳定运动;不考虑地表水垂向补给和非饱和水的运动。进而将此模型虚拟为:受可移动的铅直无厚度隔水板PP′的阻挡,左河渠不能瞬时回水,当迅速抽出隔水板PP′后,才会发生瞬时回水(图1)。
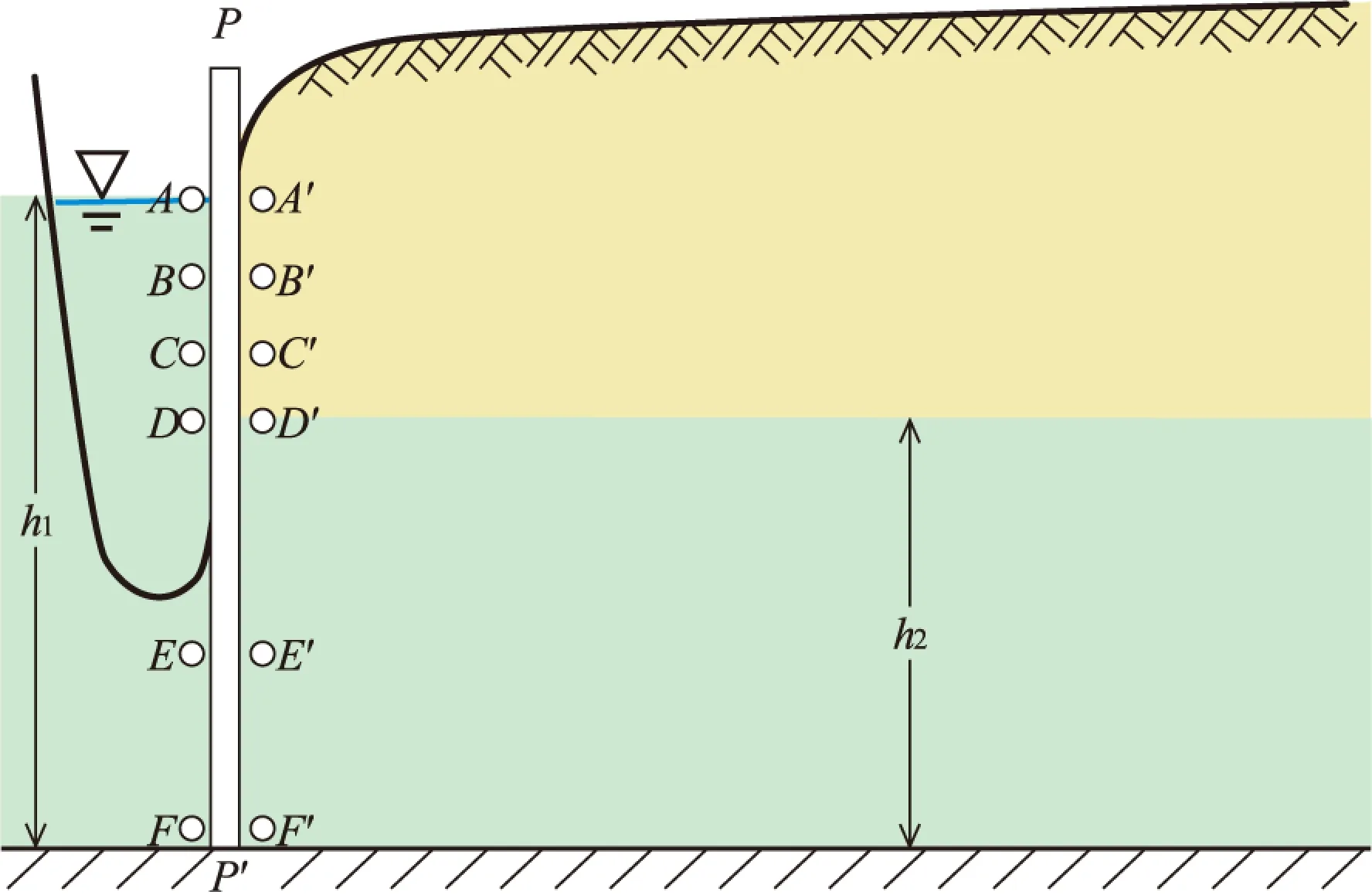
图1 潜水瞬时回水的物理模型(据文献[5]修改)Fig.1 The conceptual model of a stream recharging into unconfined aquifer
2 潜水回水初始阶段的定性-半定量分析
用水力坡度法定性-半定量分析潜水回水初始阶段非稳定运动的过程。①比较隔水板PP′左侧点A,B,C,D,E,F和右侧水平对应点A′,B′,C′,D′,E′,F′共12个点测压水头的大小(图1,A,D′分别在隔水板PP′左、右侧的液面位置,F在隔水底板上,B,C在AD间且B在C之上,E在DF间);②在迅速抽出隔水板PP′的瞬间(初始时刻),A,B,C,D,E,F点水力坡度的大小和方向如何?③微小时间段Δt后,A,B,C,D,E,F点的水力坡度的大小和方向如何变化?
2.1 测压水头大小分析
静止水体内各点的测压水头相等。A,B,C,D,E,F各点位于静止左河内,其测压水头相等,等于左河的水位h1。D′,E′,F′处于静止河间潜水内,测压水头相等,A,D′点处于水面或潜水位上,A′,B′,C′在潜水位之上,这6点只有位置水头没有压强水头。A,A′处于同一高度,B′,C′,D′高程依次降低,所以h1=HA=HA′>HB′>HC′>HD′。比较12个点的测压水头的大小,结果为:
h1=HA=HB=HC=HD=HE=HF=HA′>HB′>HC′>HD′=HE′=HF′=h2
在隔水板PP′左侧点的测压水头相等,高于右侧除A′点外的其他点,二者间存在水头差,可形成大致向右下方的水力坡度。
2.2 初始时刻水力坡度的大小和方向
分析水力坡度的大小和方向可判断地下水的运动趋势,地下水总是选择最大水力坡度的方向运动。当选择左侧界面AD上的一点,同一方向上选择不同的渗流路径长度,其水力坡度大小不等,长度越小,水力坡度越大;当终点M在右侧液面运动时,越靠近D′点水力坡度越大。比较AD上不同点的水力坡度大小时,如果以选定点至D′点作为渗流路径长度,则越在下面的点其水力坡度越大;如果选择任意的渗流路径长度,则不同点的水力坡度大小不定(图2)。
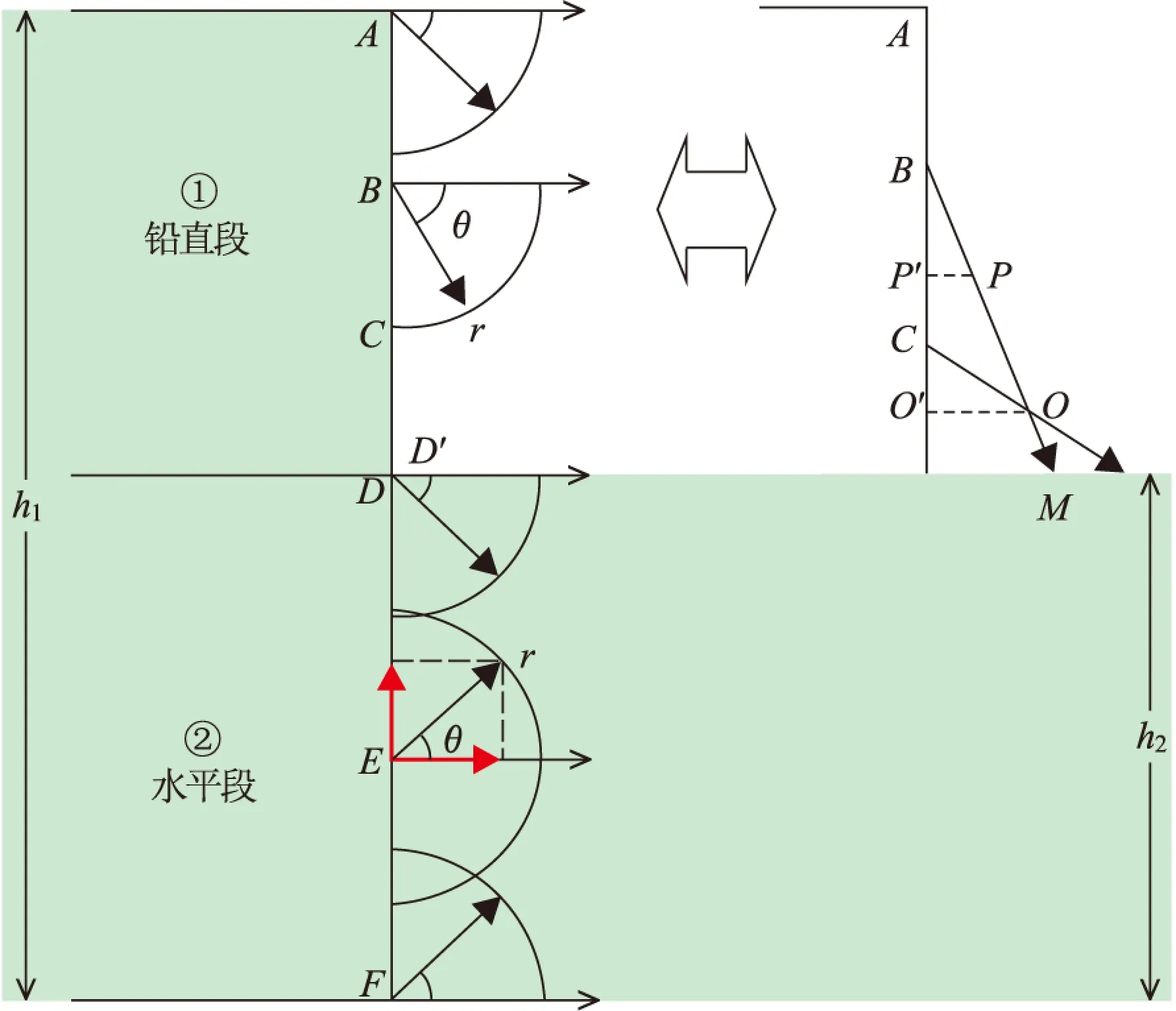
图2 初始时刻左河侧与河间地块界面上点的水力坡度分析Fig.2 The initial hydraulic gradient analysis at point on the interface between the left stream and the inter-stream arear被放大。右上部分:微小时间段Δt后,铅直段点的渗流发生冲突
以r为定长渗流路径长度,对所有点以r为半径在右侧画半圆或1/4圆(图2),规定水平向右方向为零度,顺时针旋转为正方向。这种方法适合寻找最大水力坡度方向,也可比较不同点的水力坡度。在迅速抽出隔水板PP′的瞬间(初始时刻),依据河间地块潜水位h2,将左河侧与河间地块的界面AF分为两段:高于h2的AD段,低于等于h2的DF段。界面AF上的A,B,C,D,E,F点具有代表性,只需分析这6个点的水力坡度,就可了解界面AF上所有点的情况。
(1)AD段(高于h2),即铅直段。
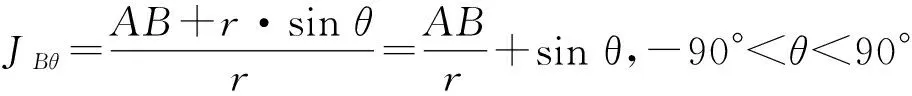
对于A点,当θ→90°时,JA→1,达到极大值,方向趋于铅直向下,所以潜水面上点的水力坡度最大只能为1。D之上附近点的渗流路径长度小于半径r,水力坡度更大,方向趋于铅直向下。
(2)DF段(低于等于h2),即水平段。
D点及其以下附近点,其右侧半圆周与河间潜水位相交,高于潜水位点的水头大,不取;F点及其附近点,其右侧半圆周与隔水底板相交;因此,D,F及其附近点仅取在河间潜水内的半圆周部分。
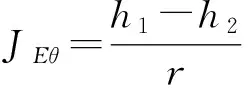
从数学角度看,渗流路径r可取无穷小,除A点外的点的水力坡度为无穷大。实际上,达西或非线性渗透定律中的水力坡度都是从宏观渗流的角度获得的,r取无穷小不在渗流研究范围。
2.3 微小时间段Δt后水力坡度的大小、方向及渗流速度
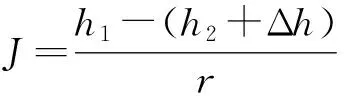
(2)铅直段AD。初始时刻,铅直段AD上点的最大水力坡度方向趋于铅直向下。经过微小时间段Δt后,任选上面B点渗流冲撞下面C点处的渗流,而受下面点的影响,B点最大水力坡度调整,方向向右偏转和变小。
如果考虑Δt时间长一些,D点之上附近点的渗流接触右侧河间潜水面后,转折为水平向右运动,可以认为,D点之上附近点有右倾直线接近平行右侧液面的水力坡度,这样的水力坡度对D点之上的点均有影响。
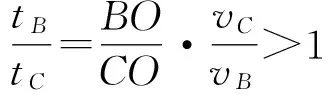
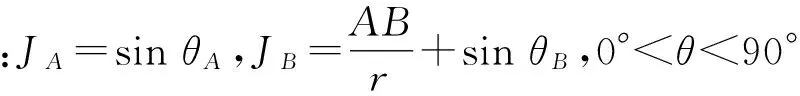
经过微小时间段Δt后,所有点的水力坡度都减小,铅直段的水力坡度方向向右偏转。
3 对水跃的正面解释
3.1 现有教材对水跃的解释所存在的问题
现有大多数地下水动力学教材中对水跃的解释,沿用1955年前苏联教材中的以反证法解释潜水井水跃(渗出面)的形成[2-3,5,9]。我们认为该解释因所依据的流网不准确,未能从根本上解释水跃形成的原因。
井内水面下是大空间中的水,井壁应看作是一个等水头面[10]。井壁等水头面与上游的等水头面ab相交于a,就说明流网是错误的,因为流网中的流面或等势面不能相交(图3)。井壁也可以不是等水头面,而与不同值的等水头面相交,ab等水头面与井壁间的区域(图3中阴影部分)不是等势体。这一点可从半无限厚承压含水层与隔水顶板相连的井壁进水不完整井获得支持,Muskat得出结论:等水头面是对称于z轴的半旋转椭球面,井的过滤器不是等水头面[5]。这种情况下,地下水可通过ab等水头面流向井,证明有侧向补给的潜水井流下部的水力坡度大于上部,而不是只有a点过水。

图3 潜水井水跃(渗出面)示意图Fig.3 Sketch of the presence of a seepage face in a pumped well
退一步说,如果流量不通过ab等水头面向井,曲面ab转为流线。产生水跃后,如果井内水位hW还是有类似ab等水头面围成的等势体,而不能进水,潜水只能从上面的渗出面入井,这也与实际情况不符(图3)。
3.2 潜水井流的特征和流网
有渗出面的潜水井流与潜水回水,经微小时间段Δt后水流有相似之处。而存在的差别有2个方面:①潜水井井壁是柱面,远小于前述河渠与河间地块界面的面积;②抽水初期的非稳定流动阶段,井壁外侧界面和井内水面都不是定水头;到稳定流动阶段,井壁外侧界面和井内水面都是定水头。潜水回水中左河面是定水头,河间地块不是定水头。可将用水力坡度方法对潜水回水初始阶段定性-半定量分析的过程和结论用于分析潜水井流,以了解潜水井流的过程和特征,获得更为准确的流网,解释产生水跃(渗出面)的原因。
井壁外侧界面以井内水面为准,可分成2段:水面之下的水平段和水面之上的铅直段(对应渗出面)(图4)。水平段点的水力坡度近相等最大且水平向井,即等水头面是以井轴为心的圆柱面,相应有最大的渗流速度,相当于承压含水层。铅直段对应渗出面,水力坡度小于水平段,越向上水力坡度越小;方向略偏离铅直向下,即等水头面略偏离垂直井壁,对应有越小的渗流速度。这个结论与近来用数值和实验方法模拟所获的结果较吻合。
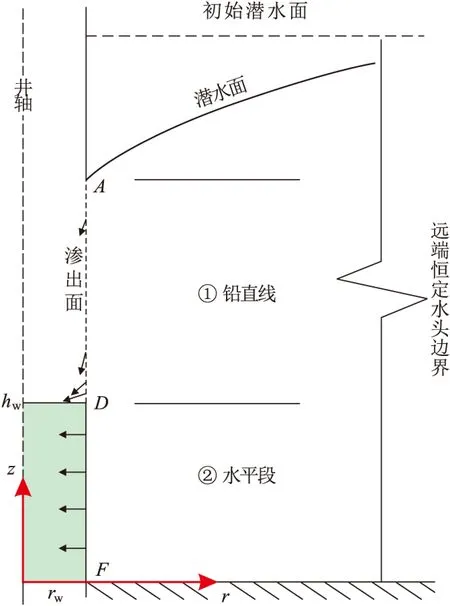
图4 井壁外侧界面渗流速度方向及分段Fig.4 Segment division and flow velocities of the soil-well interface
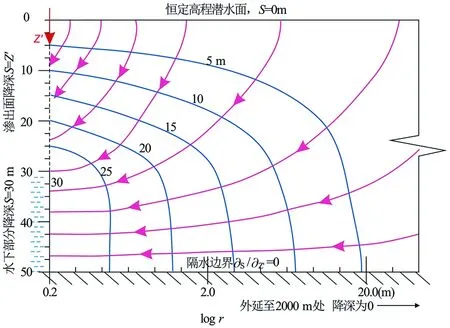
图5 潜水面保持恒定高程,有渗出面抽水完整井的流网(据文献[12]修改)Fig.5 The equipotentials and flowlines of pumped well with a seepage face in an unconfined aquifer for which the overlying water table is assumed to remain at a coant elevation
5篇文献[11-15]模拟不同情况下(完整井、不完整井、定高程潜水面、非零常流量地面、考虑不饱和水运动等)有渗出面的潜水完整井稳定流,所获得的流网和渗流速度等特征为:对应井内水柱部分,含水层中等势线几乎平行于井壁,流线水平进入井内。但沿着渗出面,流线逐渐由倾斜趋于水平线(图5)。在渗出面底部渗流速度达到最大值,井水面下的渗流速度接近相等,大于渗出面上的渗流速度(图6)。所以进井流量按长度比例来说主要来自井水面下井壁。
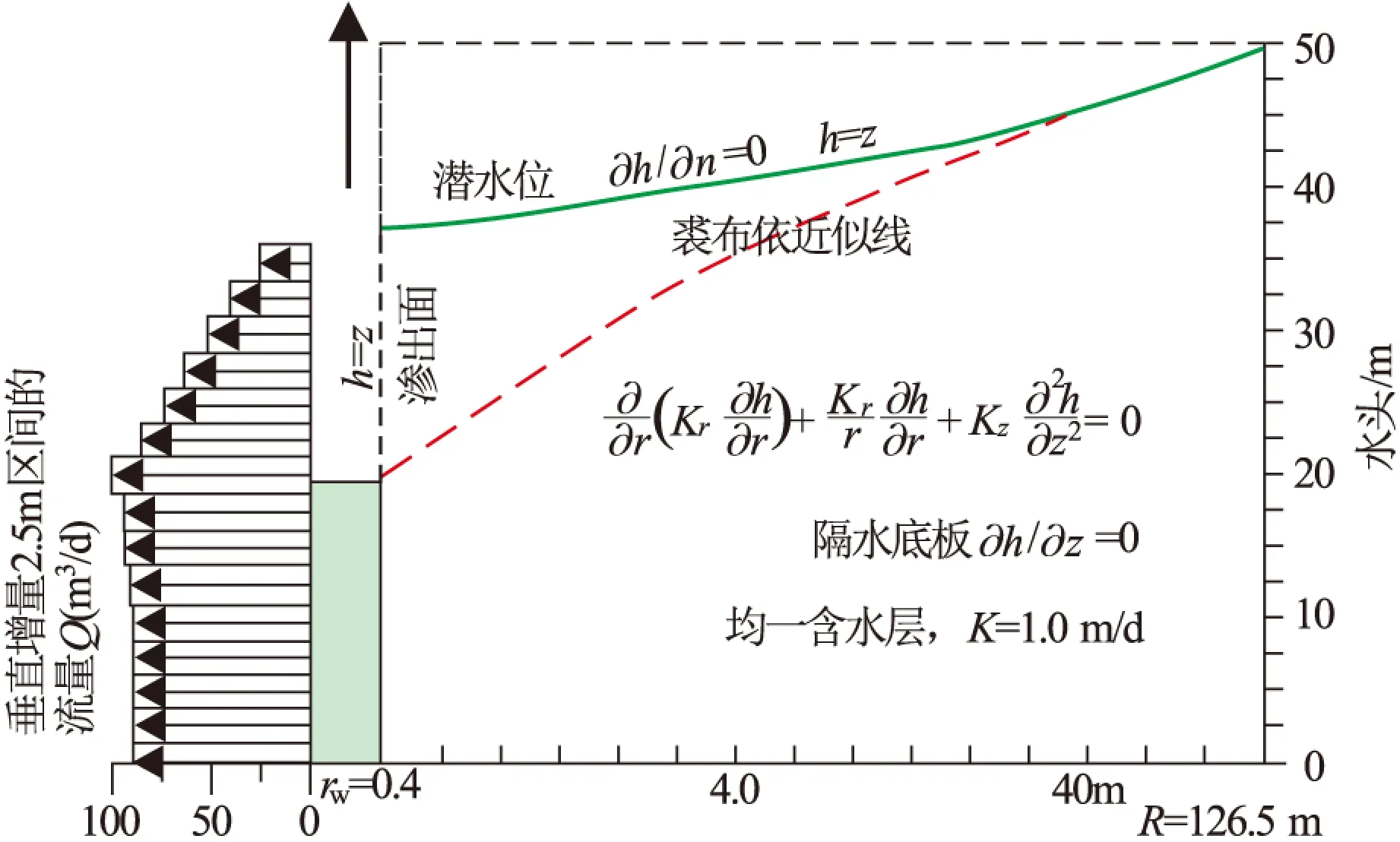
图6 有渗出面的潜水完整井稳定流数学模型及进井流量(据文献[12]修改)Fig.6 Math model flow rate of stable flow into pumped well with a seepage face in an unconfined aquifer
3.3 对水跃(渗出面) 的正面解释
式中,d为管子直径;v为断面平均流速;R为断面的水力半径;C为Chezy系数[16]。
举例,多孔介质粒径中砂级(0.5 mm),井直径300 mm[17],假设井壁内垂直井轴每层有12个圆管,管直径为77.6 mm,圆管紧密堆积后,这些圆管总横截面积略小于外井壁面积,井壁内侧的水力坡度略大于井壁外侧。井内大空间的和多孔介质的d或R差距达150倍以上。不论采用上述哪个公式,水流速度v的差距都至少在12倍以上。潜水速度还要转化为渗流速度,按孔隙度n=0.35,井中水流速度是潜水渗流速度的35倍以上,即在相同水力坡度和过水断面面积下,井内水流速度远远大于潜水渗流速度,所以抽水早期,抽水来自井储水,由于井内水位急速下降,井壁形成渗出面[18]。即使对于承压井,井外水头高于井内水位,存在井损。潜水井形成水跃大于井损。
若抽水量Q非常小,则无水跃或水跃不明显。若抽水量Q大到一定程度,就会产生明显的水跃。保持井内外大水头差,才能保证潜水既有大的平均水力坡度,又有大的过水断面面积,从而产生大进井流量。由此可证明水跃越大,单宽流量越大。
设井外水头位于A点,井内水位等于D点,水跃AD=l,井外水头AF=h0。以井轴为z轴,计算井壁AF上进井单宽流量q(图4)。单宽流量q等于水平段DF的流量q1与铅直段AD流量q2之和,应用达西定律有:
当水跃l为变量时,l∈(0,h0),单宽流量q是l的增函数,即水跃l越大进入井内的单宽流量q越大,流量就越大。井壁附近可能不适用达西定律,而适用非线性渗透定律。另外,把AD段的水力坡度考虑成h/r+1,也与实际情况略有差距,但这样处理能简化问题,结论也仍可作为定性分析的依据。
4 结论
(1)通过潜水回水初始时刻水力坡度分析,将左河侧界面分为2段:河间潜水位之上的铅直段和之下的水平段。水平段的点的水力坡度最大且相等,方向为水平向右;铅直段的点的水力坡度方向趋于铅直向下,越向上水力坡度越小。
(2)相比于初始时刻,潜水回水经过微小时间段Δt后,水力坡度都相应变小。铅直段相邻点间地下水运动发生冲突,水力坡度方向由趋于铅直向下向右偏转。可将潜水回水初始阶段定性-半定量分析的过程和结论用于分析潜水井流,有助于更好地了解潜水井流的过程和特征。
(3)地下水动力学教材中对水跃的解释多未从根本上解释水跃形成的原因。形成水跃的根本原因是:在相同水力坡度和过水断面面积下,井内大空间水流速度远大于孔隙中潜水流速度。井内水位急速下降,从而形成水跃。水跃越大进入井内的流量就越大。
致谢:在写作过程中得到2008级姬祥、闫振、张光亮同学和2009级许江、张忠杰等同学给予的启发和帮助,在此一并表示感谢!
[1] 郭东屏,宋焱勋,钱会,等. 地下水动力学[M]. 西安:陕西科学技术出版社,1994:112-115,132-133.
[2] 何俊杰,王明伟,王廷国. 地下水动力学[M]. 北京:地质出版社,2009:34-39,56.
[3] 蒋辉,曾波,潘宏雨. 地下水动力学[M]. 北京:地质出版社,2009:50-54,66-67.
[4] 吴吉春,薛禹群. 地下水动力学[M]. 北京:中国水利水电出版社,2009:53-57.
[5] 薛禹群,吴吉春. 地下水动力学[M]. 北京:地质出版社,2010:62-66,79-80,167-168.
[6] Guo W X. Transient groundwater flow between reservoirs and water-table aquifers[J]. Journal of Hydrology, 1997, 195: 370- 384.
[7] Serrano S E,Workman S R,Srivastava K,et al.Models of nonlinear stream aquifer transients[J]. Journal of Hydrology, 2007, 336: 199-205.
[8] Moutsopoulos K N. The analytical solution of the Boussinesq equation for flow induced by a step change of the water table elevation revisited[J]. Transp Porous Med, 2010, 85: 919-940.
[9] 陈崇希,林敏. 地下水动力学[M]. 武汉:中国地质大学出版社,1999:61-62.
[10] 王大纯,张人权,史毅红,等.水文地质学基础[M].北京:地质出版社,1986:34-35.
[11] Simpson M J, Clement T P, Gallop T A. Laboratory and numerical investigation of flow and transport near a seepage-face boundary[J]. Ground Water, 2003, 41(5): 690-700.
[12] Rushton K R. Significance of a seepage face on flows to wells in unconfined aquifers[J]. Quarterly Journal of Engineering Geology and Hydrogeology, 2006, 39: 323-331.
[13] Chenaf D, Chapuis R P. Seepage face height, water table position, and well efficiency at steady state[J]. Ground Water, 2007, 45(2): 168-177.
[14] Yakirevich A, Gish T J,l. Potential impact of a seepage face on solute transport to a pumping well[OL]. Vadose Zone Journal, 2010 (9): 686-696[2010-08-03]. http://www.VadoseZoneJournal.org
[15] Behrooz-Koohenjani S,Samani N,Kompani-Zare M.Steady flow rate to a partially penetrating well with seepage face in an unconfined aquifer[J]. Hydrogeology Journal, 2011, 19: 811-821.
[16] 薛禹群,朱学愚,吴吉春,等.地下水动力学[M].北京:地质出版社,1997:213-219.
[17] Fetter C W. Applied hydrogeology[M].Englewood Cliffs, New Jersey: Prentice Hall, 2001: 123.
[18] Rushton K R. Groundwater hydrology[M].England: John Wiley & Sons Ltd, 2003: 151.
The qualitative-semiquantitative analysis of the unconfined aquifer’s recharging from stream at the initial stage and explanation for presence of a seepage face in a pumped well
SUN Baoliang1, LIANG Junhong1, CUI Weili1, WU Yisong2, MA Guangzhi3
(1.CollegeofResourcesandCivilEngineering,NortheastChinaUniversity,Shenyang110004,China;2.CentralSouthResearchInstituteofMetallurgicalGeology,Yichang443003,Hubei,China;3.NorthernEngineeringandTechnologyCorporation,MetallurgicalCorporationofChinaLtd.,Dalian116600,Liaoning,China)
We use hydraulic gradient method to analyze the initial unconfined aquifer’s recharging from streams qualitatively-semiquantitatively thus provide a new visual angle for recharging process. Analysis of the hydraulic gradient of initial recharging, the left stream interface is divided into two segments, the vertical segment and the horizontal segment above and under the water table in the inter-stream area. The hydraulic gradient of the points in the segment is maximum and equal. It is to right in the horizontal direction. The hydraulic gradient of the points in the vertical segment tends downward in the vertical direction and it gets smaller upward. After a tiny period, the hydraulic gradients of any point become smaller, waters coming from adjacent points in the vertical segment collide, and the direction of the hydraulic gradient is deflected to the right. The qualitative-semiquantitative analytical method can also be employed to analyze unconfined radial flow to a pumped well. Presence of a seepage face can be explained in the way: under same hydraulic gradient and cross-sectional area, the flow velocity in big space of the well is much greater than in the pore. The water level in the well rapidly declines thus a seepage face is developed. The higher the seepage face is, the greater the rate of discharge into the well is.
unconfined aquifer; recharge; hydraulic gradient; qualitative analysis; well; seepage-face
2015-06-19; 改回日期: 2016-06-21; 责任编辑: 赵庆
孙宝亮(1970—),男,讲师,从事地下水、沉积学方面研究。通信地址:沈阳市东北大学265信箱;邮政编码:110004;E-mail: sunbaoliang@mail.neu.edu.cn
10. 6053/j. issn.1001-1412. 2016. 03. 020
P641.2
A
