PM2.5的分布规律与综合治理模型研究

文/邹靖文　张馥蕾　林宇

PM2.5的分布规律与综合治理模型研究

文/邹靖文张馥蕾林宇

随着经济的快速发展和人们生活水平的提高，环境空气质量恶化成为了亟待解决的问题之一。2012年环境保护部公布了《环境空气质量标准》，启用空气质量指数AQI作为空气质量检测指标，AQI是无量纲指数，它的分项检测指标包括6个基本检测指标：二氧化硫SO2、二氧化氮NO2、可吸入颗粒物PM10、细颗粒物PM2.5、臭氧O3和一氧化碳CO。近年来，我国大多数城市出现严重的雾霾天气，其主要原因就是大气颗粒物。而北京因市内机动车多、燃煤需求量大、工业生产规模也较大，已成为了PM2.5污染最为严重的地区之一。

本文通过多元回归分析探究了北京PM2.5的成因及分布规律，最后运用偏微分方程及多目标非线性规划模型提出了针对地区特点的治理方案。

1　PM2.5相关因素分析

PM2.5的化学组成十分复杂，不同时间和空间，其化学成分不尽相同，不同化学组成的颗粒对人体健康和大气能见度的影响亦不相同。这些影响还与化学成分在颗粒物内部和表面存在状态有关。此外不同来源的颗粒物，其化学组成也有所不同。因此研究的化学成分，即其受哪些因素影响，对来源问题的解决将会有很大帮助。PM2.5可以由硫和氮转化而成，除此之外，可燃物的不完全燃烧也会产生颗粒物，并且附有一氧化碳等，这些污染物会与大气产生化学反应而生成二次颗粒物，使气体转化为粒子。而且大气中的臭氧是否与PM2.5有关系现在仍有争议。

1.1数据来源及处理

本文数据来源于北京市环境保护监测中心实时空气质量数据发布平台，时间跨度为2015年1月1日至2015年12月19日，共352天，数据频率为小时。共35个观测点，每个观测点含有AQI及6个指标的观察值。对每个观测点每项指标的0时-23时数据求平均值，得到当天该观测点该项指标的24小时平均值。之后对各观测点当日该指标的数据求均值，得到北京市当日该指标的平均值。

1.2相关性分析

图1显示了2015年1月1日至2015年12月19日北京市空气质量观测指标CO、NO2、O3、PM10、SO2及PM2.5的时间变化序列图。可以看到不同污染物在多数的时间内趋势大致相同，呈线性关系，PM10 与PM2.5具有较高的同步性。

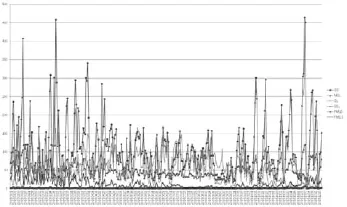
图1　2015年6项指标平均浓度变化

进一步地，Pearson相关系数（表1）展示了各指标之间的相关系数。可以看到，PM2.5与PM10、NO2和CO的相关性系数都在0.8以上，与SO2的相关性较弱，与O3呈微弱的负相关。除PM2.5之外其他五个指标的相关性系数也较高。

从表1结果分析得出，PM2.5的大小首先与空气中的可吸入颗粒物PM10呈现最大程度的正相关。PM2.5指空气中当量直径小于或等于2.5微米的细颗粒物，PM10则是指空气中当量直径小于或等于10微米的颗粒物，其中包含着PM2.5。其次，CO和NO2则是PM2.5产生的重要影响因素，对于其来源与控制需要重点分析。由于臭氧和PM2.5都是造成雾霾天气的元凶，造成空气污染，但PM2.5本身和臭氧并没有很强的相关性，这就说明臭氧和PM2.5的治理是需要分开同时进行的，而不是解决一个，另外一个就能自然解决。

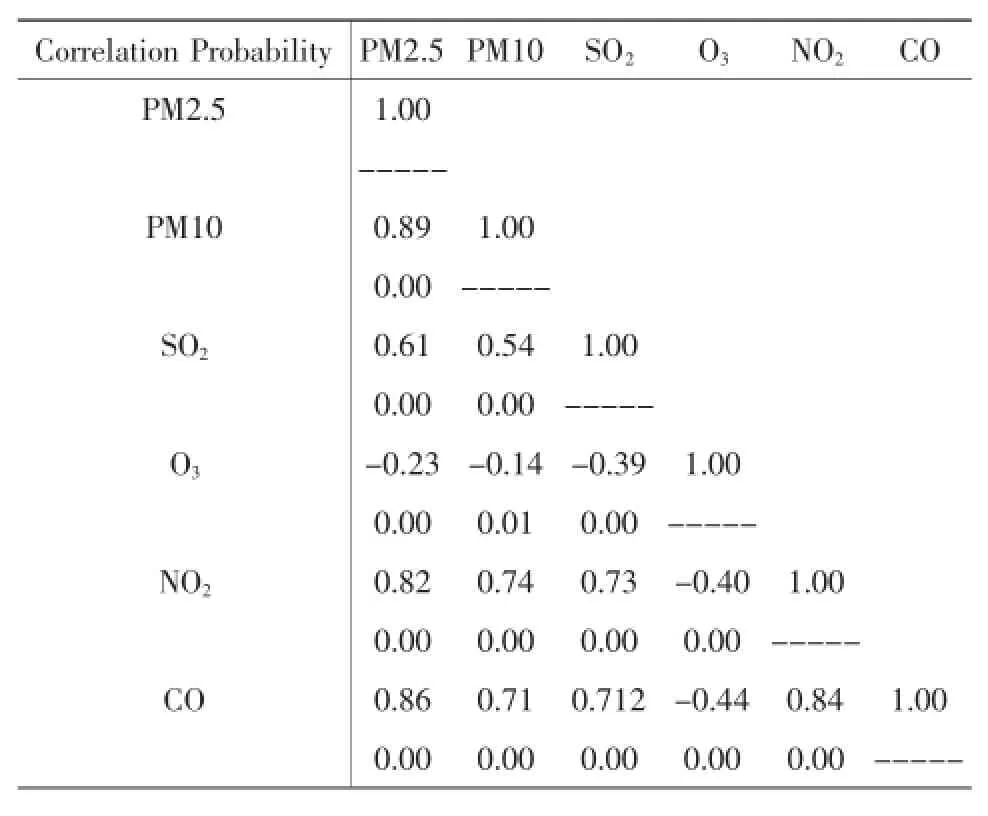
表1　指标间的相关系数表

1.3多元回归分析

一般地，影响试验指标的因素不止一个，假设它们之间的线性关系如式（1）所示：

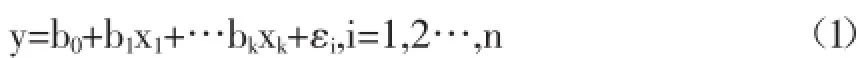
其中，y为可观察的随机变量，k为解释变量的数目，bi为回归系数，xi为非随机的可精确观察的变量，为服从N（0,1）的独立同分布的随机变量。

本文选取文中所述北京市数据作为研究对象，建立以PM2.5浓度为因变量，其余5项指标为自变量的回归方程，由表2，求得回归方程如下：

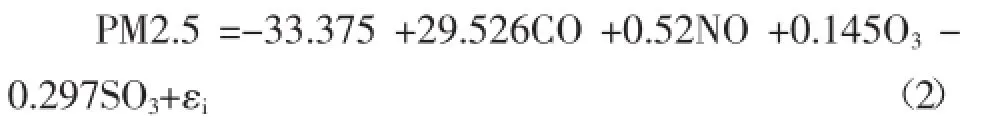
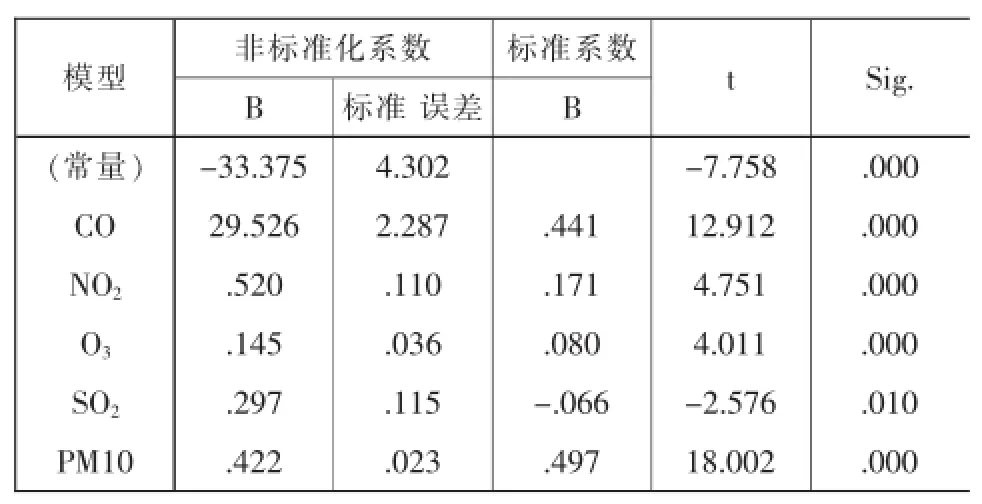
表2　回归结果a

表3　模型汇总b

从表3看出，方程变量系数均在5%显著性水平上显著，R方达到0.902，方程拟合效果理想。

从回归方程中看出，与PM2.5形成关系最大的是空气中的CO浓度，其次为NO2，这和相关系数的结果是一致的。而北京二次无机气溶胶、工业污染、燃煤、土壤尘、生物质燃烧、汽车尾气与垃圾焚烧等活动均伴随CO以及NO2的大量产生。

2　PM2.5的时空分布规律及污染评估

北京市共有35个空气质量监测站点，其中城区环境评价点12个，郊区环境评价点11个，如表4所示。

表4　城区城郊监测站点名称

环境保护部新修订的《环境空气质量标准》中规定了空气质量分指数及相关信息。其中AQI在0-50、51-100、100-150、151-200、201-300和＞300分属一级、二级、三级、四级、五级和六级。一、二级对大多数人群活动影响不大。为了能够正确区分PM2.5浓度在不同范围之内的分类，列出空气质量分级指数的级别与对应污染物浓度的限值进行参照，如表5所示。

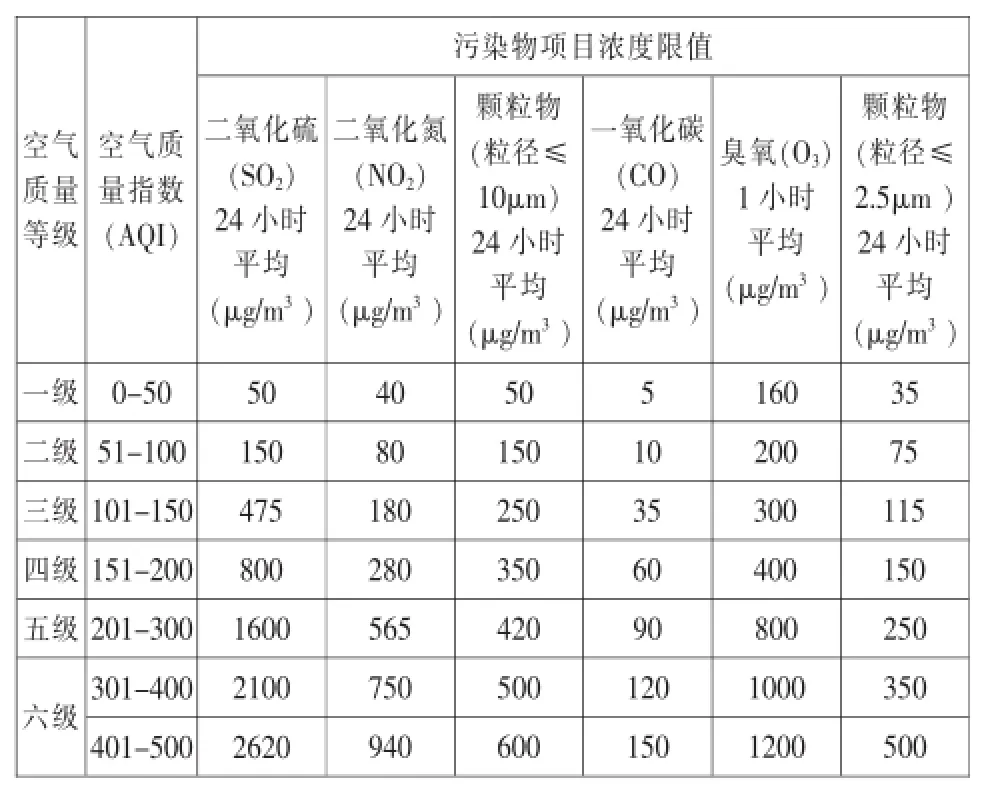
表5　空气质量指数与预定的污染物项目浓度限值

由于将各个监测点浓度分别展示过于繁杂，因此本文将样本区间内的监测点作平均值，然后比较城区和城郊各监测点的PM2.5浓度变化。图2中显示，两者在一年中的变化趋势基本一致，但整体而言城郊的PM2.5浓度要高于城区。两者的变化趋势一致，或者说城区和城郊的PM2.5浓度具有较显著的正相关性，说明不同月份对于PM2.5浓度的影响同时作用在城区和城郊。而城郊的PM2.5浓度更高，很可能来源于周边地区，尤其是河北省的工业污染，以及当地自有的工业产生的污染。城区第三产业比重较大，工业污染总体较城郊要少，因此PM2.5浓度较低。

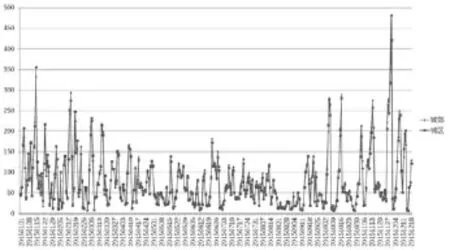
图2　城区及城郊监测点平局浓度变化图

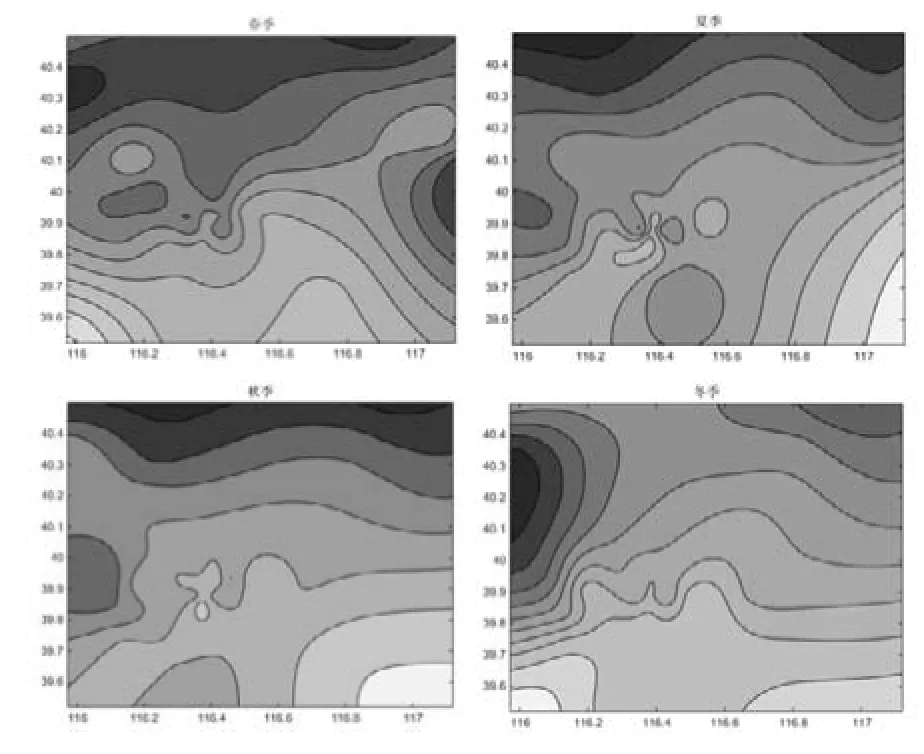
图3 35个空气质量监测点分季节PM2.5浓度等值图

图3中四幅图分别表示了春夏秋冬四季各监测点PM2.5浓度的空间等值线图。其中颜色越深表示PM2.5浓度越高。横轴表示经度（东经），纵轴表示纬度（北纬）。总体而言，PM2.5浓度呈现北低南高的分布。重点污染区域集中在房山、通州两区，这主要是由于两区本地的工业污染及周边地区的工业污染带来的影响。而延庆、怀柔和密云三个区的空气质量较好，这与当地的森林覆盖率较高、生态环境保护较好有关，这也说明了北京市建立生态涵养区的科学性。可以看到，在城中心区范围内（北纬39.8°至40°，东经116.3°至116.4°）PM2.5浓度较周边地区偏高，这主要由于城市中心区设立了五个交通监测点，这些监测点的数据由于大量汽车尾气的存在会相对偏高，从而使得了城中心范围的PM2.5检测水平较高。

3　PM2.5专项治理计划

有关研究表明，北京市PM2.5约60%来源于燃煤、机动车燃油和工业使用燃料等燃烧过程。在PM2. 5的传统治理方法中，工业区的外迁虽然会解决大型工业城市雾霾天气的问题，但是工业区从一个区域迁移到另外一个区域，不仅会增加企业生产的成本，还会造成污染区的扩散。再者，企业生产过程中技术的改进会控制污染源，短时间内要求大量的企业进行生产过程中技术升级，硬件设施可能会在短时间满足这一要求，但软件设施（如相应的管理人员，专业的技术操作人员等）则需要长时间的积累才能满足这一要求，并且技术升级对大型生产企业可能会实现，但对众多的中小型企业在成本上则难以承受。

所以此治理计划旨在五年内，结合目前该地区的经济、社会和环境等，在保证区域经济持续发展的同时，采取各种措施，解决PM2.5污染的问题。制定计划与北京市特殊的地区情况分不开。北京市与河北省众多工厂相邻，北京市内的机动车尾气排放也很严重。因此可以采用渐进性的治理计划，即已经投产的大型工业项目继续运转，但同时也要解决经济转型中的各种问题，努力优化产业结构，加快形成战略性新兴产业的新优势，从而在新兴产业中占据有利位置。同时，由于经济大体转型期约为3年到7年时间，因此，这种“治根”的方法可能在短时间内对PM2.5污染的问题效果不大，但一旦经济从整体上向第三产业转移，同时积极进行环保技术创新，那么3～7年左右北京市PM2.5污染情况将会有明显改善。

4　综合与专项治理结合计划

根据所得数据，北京地区PM2.5的平均浓度为77.78μg/m3（三级），若希望在未来五年内逐年减少PM2.5的年平均浓度，最终在五年后达到PM2.5的年平均浓度为35μg/m?（一级），经综合考虑，本文给出如下综合与专项治理结合治理计划。该计划可以分三期实现。

（1）第一期（第一年、第二年）：初见成效，PM2.5值相比于当前降低20%。

（2）第二期（第三年）：持续改善，PM2.5相比于第一期降低20%。

（3）第三期（第四年，第五年）：基本达到目标，PM2.5值相比于第二期降低30%。

详情可见表6和表7。

表6　未来五年PM2.5降低百分比

表7　未来五年PM2.5降低额度

假设在各种措施的治理下，PM2.5值和年份数存在函数关系，PM2.5值为y，年份数为x。结合PM2.5值的变化趋势，假设函数：

其中a,b为任意实数。

设定2015年北京市PM2.5年均值为80μg/m3。五年后，PM2.5值降低到35μg/m3，则

求解a、b值：a=-0.3053，b=80.31，则目标函数为

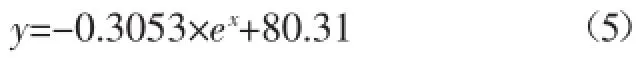
目标函数图见图4。

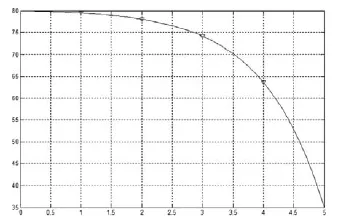
图4　PM2.5变化趋势

由图4可以清楚地看到PM2.5值的变化趋势，在刚开始的两年PM2.5值变化额很小，但在两年以后的长期发展中，PM2.5值的变化幅度迅速增加，直至第五年底，PM2.5值达到目标值。

4.1比例削减规划模型

采用比例削减规划模型（proportionalrollback planningmodel），污染源排放的污染物数量的削减，将导致大气环境中污染物浓度的等比例下降。由此确定的最简单的控制方案是要求各个排放源按其排放的负荷比例进行削减。根据上述假设，一个地区的气象条件相对一致，污染源位置不变，若对所有污染源排放的污染物都以相同比例削减，则该地区污染物的浓度也将以同比例下降。

达到预定PM2.5减排计划的同时希望经费投入较为合理，当然经费投入越少越好，问题中给出了综合治理费用，每减少一个PM2.5浓度单位，当年需投入一个费用单位（百万元），专项治理投入费用是当年所减少PM2.5浓度平方的0.005倍（百万元）。

4.2方案合理性评估

在上述模型求解中，比较当满意度F限值a2不同时，对应的最小投入总费用，见表8。

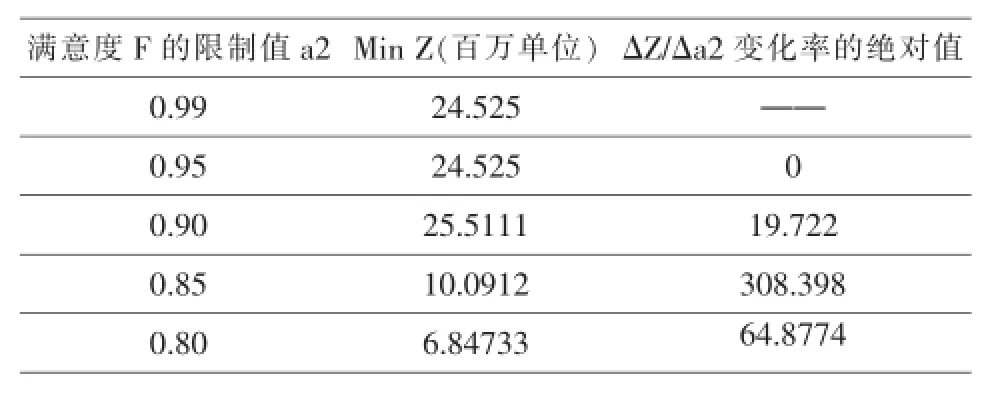
表8　合理性评估

ΔZ/Δa2变化率的绝对值即为增加治理费用投入对增加满意度的边际效用，综合表中数据，当满意度达到0.85时费用投入相对较小，且边际效用最大。因此选择0.85作为满意度限值。所得结果中，每年综合治理所花费用大于综合治理。专项治理针对PM2.5的成因进行治理，如从SO2，NO2，PM10等源头治理，效率较高。而综合治理则总整体上对PM2.5污染物进行治理，并且包括补贴、管制等其他费用，因此对提升公众满意度具有明显的效用。

模型求解出每年综合治理和专项治理减少的PM2.5年平均浓度如表9所示。

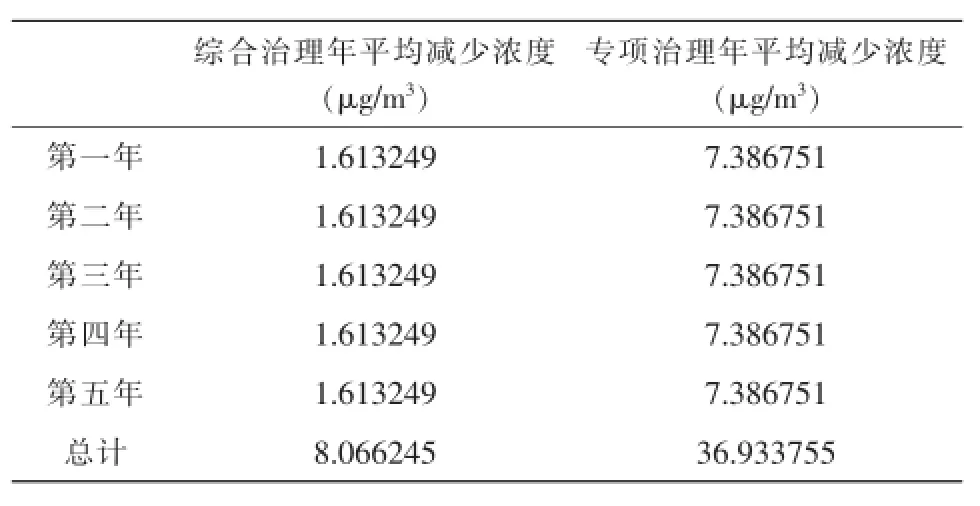
表9　综合治理和专项治理PM2.5年平均减少浓度

5　结语

本文利用北京环保局的PM2.5数据，结合图表分析法，分析了北京PM2.5的时空变化特征。总体而言PM2.5浓度呈现北低南高的分布。重点污染区域集中在房山、通州两区，而延庆、怀柔、密云三个区的空气质量较好。最后综合考虑对PM2.5的综合治理与专项治理，结合防治满意度构建多目标优化模型，并根据投入-改善效率对模型进行合理评价。

邹靖文（1994-），女，中国政法大学商学院成思危现代金融菁英班学生，本科在读，研究方向为数理金融；张馥蕾（1995-），女，中国政法大学商学院成思危现代金融菁英班学生，本科在读，研究方向为数理金融；林宇（1995-），女，中国政法大学商学院工商管理专业学生，本科在读，研究方向为企业战略管理。