改进蚁群算法的多约束质量最优路径选择

马荣贵,崔 华,薛世焦,郭 璐,袁 超

(长安大学信息工程学院,陕西西安 710064)

改进蚁群算法的多约束质量最优路径选择

马荣贵,崔 华,薛世焦,郭 璐,袁 超

(长安大学信息工程学院,陕西西安 710064)

在交通拥堵日益严重的形势下,当今大众对行车过程中的道路质量评定标准发生了重大变化,如何避开拥堵,寻找最优的出行路径,已成为智慧城市建设大力推进背景下亟待解决的重要科学问题和社会问题.首先,定义了质量最优路径的概念,并构建了多约束质量最优路径模型;然后,为更有效求解该模型实现最优路径选择,在基本蚁群路径寻优算法的基础上,通过增加算法对道路通畅度、道路舒适度、道路费用等路径质量信息的实时感知,改进了状态转移规则中的启发函数和信息素更新算子,提高了算法自适应于路径质量信息的动态调整能力.实验结果表明:文中改进的蚁群算法与其他蚁群路径寻优算法相比,明显提高了路径寻优的正确率和收敛速度,能够更加快速、准确地进行路径选择.

多约束路径选择;质量最优路径;蚁群算法;信息素更新;启发函数

随着私家车的日益增多,交通安全及交通拥堵问题也越来越严重,如何诱导车辆在出行时选择“高质量”的路线是一个普遍的难题[1-2].把“最优路径”定义为只考虑最短路径或者最少费用等单一约束的最优问题已经不能满足大众的需求,而最优路径搜索本质上是在路网中寻找能够同时满足驾驶者期望的多个约束条件且某个单项目标值最小的路径.在路径寻找中具有两个以上限制的路径问题是非确定多项式(Nondeterministic Polynomial,NP)问题,采用传统的搜索算法无法解决,而蚁群算法是一种具有正反馈机制、分布式并行机制、自组织机制等特征的优化方法,能够在道路搜索过程中感知周围环境的实时变化,用于寻找最优路径具有极大的优势.文献[3]采用基本蚁群算法解决最优路径导航问题;文献[4]引入路径权值矩阵改进了基本蚁群问题的转移规则,提高了向最优路径转移的概率,改善了最优路径导航效果;文献[3-5]中研究的最优路径仅与行车距离有关;文献[6]考虑了蚂蚁的动态变异,并对基本蚁群算法的信息素浓度更新规则进行了改进,实现了对动态最短路径的实时导航,该改进方法更有利于蚂蚁找到最优路径,其最优路径仅与行车距离有关.

以上文献利用蚁群算法构建路径优化选择算法时,不仅蚁群算法本身的路径搜索性能有待改善,而且路径导航的约束条件也不能满足当今实际应用的要求.文献[7-9]提出了“路径质量”概念和“可靠路径”概念,但这些定义大都限定在未饱和的交通状态下选择最优路径,这显然与当今日益拥堵的交通状况不相适宜.笔者考虑到交通拥堵、道路舒适性等诸多影响驾驶者选择行车路径的因素,结合当今大众对最优路径的评定标准,将最优路径的概念重新定义为“多约束质量最优路径”,即一条好的路径应是满足行车距离、到达时限、行驶费用、实时道路交通状况、行车舒适性等多约束条件的距离最短道路,并通过改进蚁群算法,在车辆出发地和目的地之间的路网中快速准确地求解出按照多约束条件选定的一条质量最优路径.

1　质量最优路径模型

传统意义上的最优路径指的是车辆在起点和终点间选择一条距离最短的路径,这时质量最优路径仅与行车距离有关.考虑到当今道路交通状况比较拥堵,驾驶者希望避开拥堵路段,另外,驾驶者在选择路径时会考虑多方面的因素,如选择从起始点到目的地距离最短的道路,希望花费时间在预期范围内,希望过路费、燃油费等成本不太高,希望道路通畅而不希望道路限行或由交通事故、施工等引起的交通拥堵,希望道路舒适度高.道路舒适度取决于道路级别、道路宽度(车道数)、路面平整度、光滑度、附着度等指标以及路边环境的美化状况、交通事故发生率、道路限速、邻接交叉口的信号配时等.文中依据当今大众对路径质量的评定标准,将质量最优路径模型定义为如下的多约束优化问题:

其中,cij表示道路节点i与节点j之间的长度;s为连接o和d之间的一条路径,o代表起始点,d代表终止点;如果t时刻弧cij在路径s上,则;否则,;NS表示路网的节点集;T表示所选路径实际花费的总时间;Tb表示出行允许的时间上限;cfij为路段cij的舒适度,cfij∈(0,1),越接近1表示该道路的舒适度越好;cfb表示驾驶员能接受的道路舒适度的下限;jij为路段cij的实时道路交通情况,jij在(0,1)之间取值,越接近1表示交通畅通情况越好;jb表示驾驶者能接受的道路畅通度的下限,当函数值为0时,表示该道路严重拥堵或者该道路禁止通行;C表示所选路径的总费用;为所走路径的收费;(1+为所走路径需要的燃料费用;fij为路段cij的收费金额;k表示平均每公里的燃料费用;g表示车辆行驶在不同畅通状态路段的耗油量增加的百分比;fmax表示驾驶员能容忍的道路费用的最大值.

2　改进的蚁群算法

在基本蚁群算法中[10],蚂蚁依据状态转移规则选择下一个道路节点,即

2.1改进的启发函数

基本的蚁群算法不考虑蚂蚁遍历节点的方向性,所以将启发函数ηij(t)设置为蚂蚁在t时刻在道路节点i与待选节点j的距离dij的倒数.这种启发函数会导致路径寻优问题中的蚂蚁贪图单步最短而偏离行进方向,寻找到的路径未必是总体最短路径.为此,文中综合考虑了当前位置与转移后位置之间的距离、蚂蚁已走过的路径距离以及转移后位置与目的地之间的距离,将启发函数修改为

其中,L(i)表示从起点到节点i蚂蚁已经走过的道路长度;Djd为j点到目标点d的距离.式(4)所示的改进的路径选择启发函数,有效加强了路径搜索的方向性和准确性,可引导蚂蚁在行进过程中有目的地不断向目标点靠近,保证了蚂蚁所走过的总路程是最短的,满足文中寻求多约束条件下最短路径的目标.

2.2改进的信息素更新规则

为诱导蚂蚁更快更准地找到满足约束的质量最优路径,构造函数F(b)将质量最优路径模型的多约束条件有效融合到蚁群算法中,让蚁群实时感知道路的舒适度、畅通度等质量状况,指导蚁群及时调整路径搜索策略,即

其中,p和q表示从起点到终点经过的路段的数目;F1、F2、F3和F4分别表示路径b上的费用、行驶时间满足驾驶者时间要求的程度、平均畅通情况和道路平均舒适度;χ、γ、λ和μ为正实数,分别表示驾驶者对道路费用、时间、畅通度和舒适度的重视程度.为诱导蚂蚁以较大概率选择质量最优路径,在信息素全局更新时,考虑了路径质量状况,并通过强化最优路径上的信息素和弱化最差路径上的信息素,促使蚂蚁选择最好路径而放弃最差路径.改进的信息素浓度更新公式为

其中,ρ是信息素挥发程度因子,F(b)是式(5)所述的反映路径质量状况的函数,Lbest和Lworst分别表示算法找到的最好路径s*和最差路径s′的长度,ε为信息素强化因子.为有效避免各个路段信息素浓度差异过大,而导致算法陷入局部最优,信息素浓度进行如下限制:

3　仿真与分析

图1为道路网络拓扑图,每条边某时刻的属性用一个5元组(len,spe,f,j,cf)来表示,依次代表边上的距离(km)、允许速度(km/h)、通行费用(元)、实时道路畅通度和道路的舒适度,并假设车辆在行驶过程中,当接近任何路口时可及时获得待选路网各路段未来15 min的交通信息预测值.实验参数设定如下:允许的行车时间Tb≤7 h道路的畅通度j>0.4,所走道路舒适度cf>0.3;基本蚁群和半改进蚁群算法中,α=1,β=3,m=14,n=14,Q=10,ρ=0.55,Nmax=100;改进的蚁群算法中,α=2,β=5,m=14,n=14,Q=10,ρ=0.55,Nmax=100,Tb=7,k=0.5,τmax=20,τmin=1,ξ=0.01,χ=0.01,γ=1,λ=5,μ=5,τ0=τmax.

图1　道路拓扑图

为验证文中提出的基于改进蚁群算法的质量最优路径选择方法的性能,进行了如下实验.实验结果如表1和图2所示.表1是100次Monte Carlo仿真实验得到的各算法性能结果.从表1可以看出,基本蚁群算法和半改进蚁群算法找到的最优路径在图1中由箭头标注,此路径也是从起点到终点的总体最短路径,但是此路径途径拥堵路段及个别路段的舒适度很低,不满足文中定义的多约束质量最优路径.改进蚁群算法找到了文中定义的多约束质量最优路径1-5-7-11-14,避开了拥堵路段,途径的每个路段的舒适度都很高,而且寻优率和寻优时间都有很大的改善.说明在文中基于质量最优路径模型对信息素更新准则和启发函数的改进是有效的,使得文中提出的改进蚁群算法具有良好的路径寻优性能,在路网拥堵情况下成功选择了畅通或较低拥堵度的路段,而避开了拥堵更严重的路段.从图2可知,文中改进的蚁群算法经过约80次迭代便可找到最优路径,而基本蚁群算法、半改进蚁群算法则需要更多的迭代次数才能收敛到最优路径,说明了文中对基本蚁群算法在启发函数和信息素更新准则两方面所进行的改进的有效性,增强了算法依据道路属性实时变化而产生的正反馈作用,提高了算法的收敛速度和路径寻优速度.而表1所示的3种蚁群算法的运行时间同样体现了改进蚁群算法具有最快的寻优速度.

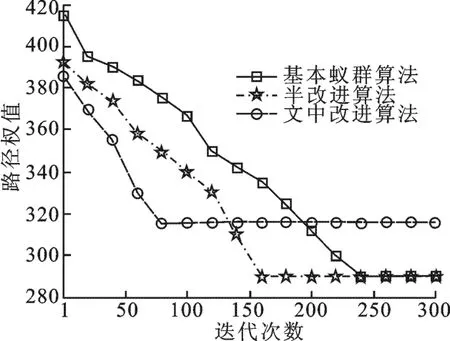
图2　3种算法的收敛曲线

表1　蚁群算法的路径寻优结果

4　结束语

针对最优路径选择问题,根据当今大众对路径质量的评定标准,文中定义了质量最优路径模型,进一步地,为更高效求解多约束条件下的质量最优路径问题,通过定义新的信息素更新因子和新的状态转移启发因子对基本蚁群算法进行了改进,并对提出的改进蚁群算法的路径寻优性能进行了实验验证.实验结果表明,文中提出的导航算法较基本蚁群算法在路径寻优速度和正确率方面有较大提高.

[1]YAO E J,LANG Z F,YANG Y.Vehicle Routing Problem Solution Considering Minimising Fuel Consumption[J]. IEEE Transactions on Intelligent Transportation Systems,2015,9(5):523-529.

[2]LIN X,LO H K.Adaptive Vehicle Navigation with EN Route Stochastic Traffic Information[J].IEEE Transactions on Intelligent Transportation Systems,2014,15(5):1900-1912.

[3]HAMZHEEI M,FARAHANI R Z,RASHIDI-BAJGAN H.An Ant Colony-based Algorithm for Finding the Shortest Bidirectional Path for Automated Guided Vehicles in a Block Layout[J].The International Journal of Advanced Manufacturing Technology,2013,64(4):399-409.

[4]HUANG M,DING P.An Improved Ant Colony Algorithm and Its Application in Vehicle Routing Problem[J]. Mathematical Problems in Engineering,2013,2013:1-9.

[5]SCHYNS M.An Ant Colony System for Responsive Dynamic Vehicle Routing[J].European Journal of Operational Research,2015,245(3):704-718.

[6]LISSOVOI A,WITT C.Runtime Analysis of Ant Colony Optimization on Dynamic Shortest Path Problems[C]// Proceedings of the 2013 Genetic and Evolutionary Computation Conference,Association for Computing Machinery.New York:ACM,2013:1605-1612.

[7]REED M,YIANNAKOU A,EVERING R.An Ant Colony Algorithm for the Multi-compartment Vehicle Routing Problem[J].Applied Soft Computing,2014,15:169-176.

[8]MAVROVOUNIOTIS M,YANG S X.Ant Algorithms with Immigrants Schemes for the Dynamic Vehicle Routing Problem[J].Information Sciences,2015,294:456-477.

[9]NIE Y,WU X.Shortest Path Problem Considering on-time Arrival Probability[J].Transportation Research Part B: Methodological,2009,43(6):597-613.

[10]MAHI M,BAYKAN O K,KODAZ H.A New Hybrid Method Based on Particle Swarm Optimization,Ant Colony Optimization and 3-Opt Algorithms for Traveling Salesman Problem[J].Applied Soft Computing,2015,30:484-390.

(编辑:齐淑娟)

Improved ant colony algorithm for the optimal-quality-path routing problem with multi-constraints

MA Ronggui,CUI Hua,XUE Shijiao,GUO Lu,YUAN Chao
(School of Information Engineering,Chang’an Univ.,Xi’an 710064,China)

As the traffic congestion becomes more and more serious,the public evaluation standard for the road quality during driving changes greatly.How to avoid congestion to find the best way to travel has become an important scientific issue and social issue urgent to address in the context of building a smart city.Thus this paper first defines the novel concept of optimal path with multi-constraints and models it. Then,in order to solve the proposed model more efficiently,we improve the state transition rules of the heuristic function and pheromone update operator based on the classical ant colony algorithm by increasing the path optimization algorithm’s awareness of real-time path quality information,such as traffic conditions,resulting in the strong dynamic adjustment ability of our proposed path optimization algorithm to path information.Simulation results show that our proposed ant colony algorithm can find the optimal path with multi-constraints more accurately and more quickly than other ant colony algorithms.

multi-constraint path routing;optimal quality path;ant colony algorithm;pheromone update;heuristic function

TP751

A

1001-2400(2016)03-0185-05

10.3969/j.issn.1001-2400.2016.03.032

2015-08-24

国家“863”计划资助项目(2012AA112312);中央高校基本科研业务费专项资金重点资助项目(310824152009)

马荣贵(1967-),男,教授,博士,E-mail:rgma@che.edu.cn.