中、法初中教材中方程内容的比较研究
2016-12-07尚亚明华东师范大学数学系
尚亚明(华东师范大学数学系)
张玉环(河南大学数学与统计学院)
中、法初中教材中方程内容的比较研究
尚亚明(华东师范大学数学系)
张玉环(河南大学数学与统计学院)
对中国与法国初中教材中方程内容进行量化分析和质性分析,并得到一些启示.量化分析方面,中国人教版教材对广度、深度、例习题的要求均高于法国;质性分析方面,中国人教版教材重视对知识的探索与拓展、对具体问题的解决,而法国教材注重学生自我体验感悟、对知识的各个击破,以及逐步引导学生求知.
中、法教材;方程内容;比较研究
一、问题的提出
方程作为初中数学教材的一个重要组成部分,是初中生用来解决问题的最主要手段和工具.方程具有深远的数学思想,甚至可以不断深入影响许多学科发展.因方程内容在整个数学体系中的重要位置与作用,著名数学家陈省身对“解方程”问题曾给出很好的评价.研究者普遍认为,教师在日常教学中相当依赖教材,在很大程度上依据所使用的教材决定教什么,怎么教,以及给学生布置哪些习题等.众所周知,位于欧洲西部的法国在历史上对数学的发展有着重大贡献.因此,选择中国和法国两个国家的初中教材作为研究对象,以期对中国教材方程部分的编写与使用提供一定的参考与借鉴.
二、研究设计
1.研究对象
人教版《义务教育教科书·数学》(以下统称“人教版教材”)是目前在国内影响较大、使用面较广的教材.现选取七年级上册、七年级下册、九年级上册这三册包含方程内容的教材进行比较研究.
2.研究方法
主要对内容广度、内容深度、例习题难度进行量化分析;对核心知识点的处理、实际应用进行质性分析,以此推断中国与法国初中阶段教材中方程部分设置的异同点和各自特点.
(1)知识点的确定方法.
知识点即教材正文中所出现的所有数学概念、数学命题(公理、定理、法则、公式等).根据下面三条原则确定知识点:①依据《义务教育数学课程标准(2011年版)》,对比两国的教材,并参考相关资料;②如果两个概念区分度不大时,算做一个知识点,例如二元一次方程和二元一次方程组;③虽然函数和方
程关系很密切,但现在考查的是“方程”模块,在“方程”模块中没有出现函数与方程的关系,故不作为知识点.确定的知识点如表1所示.

表1:两国各模块所含知识点
【说明】表1中列方程、二元一次方程组,三元一次方程组、一元二次方程、一元二次方程的解、公式法、根与系数关系是人教版教材比SM教材多的知识点.其中、方程的性质、根与系数的关系是性质,代入消元法(在SM教材中叫代换消元法)、加减消元法(在SM教材中叫高斯消元法)、配方法(在SM教材中叫完全平方法)、公式法、因式分解法(在SM教材中有提公因式法、平方差公式法)是算法,方程、方程的解、二元一次方程组、二元一次方程组的解、三元一次方程组、一元二次方程、一元二次方程的解是概念.
(2)内容的比较方法.
将方程知识分为一元一次方程、二元一次方程组、一元二次方程三个模块,对内容广度、内容深度进行比较.两个国家教材中所包含的知识领域、概念与命题的数量作为广度的指标,深度比较指标如表2所示.
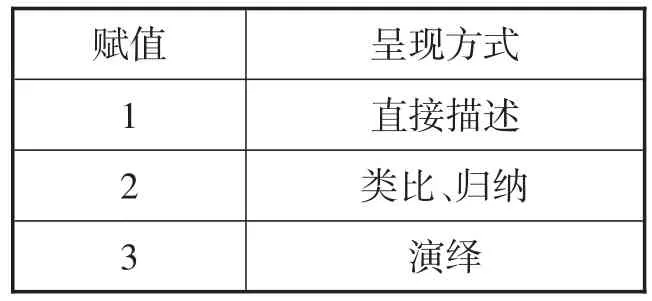
表2:内容深度水平指标
(3)例、习题的比较方法.
选取知识点数量、背景、要求水平三个指标来进行比较,见表3.

表3:例、习题水平指标
其中di依次分别表示知识点数量、背景和要求等因素的取值;dij表示第i个难度因素的第j个水平的权重;nij表示一组题目中属于第i个难度因素的第j个水平的题目的个数,其总和等于该题目的个数n.
三、研究过程与结果
1.量化分析
(1)内容广度比较.
从表1可以看出,人教版教材中“方程”部分有19个知识点,内容广度为19;SM教材有13个知识点,内容广度为13.两国对相同概念的定义方式有所差异,主要体现在表述的不同.例如,对方程的定义,人教版教材的定义为含有未知数的等式是方程;SM教材的定义为方程是一个等号和一个或多个未知数(常用字母表示)组成的表达式.前者强调方程是等式,后者强调方程是表达式,且表述更详细,更彻底.再比如,对方程的解的定义,人教版教材为,一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解;SM教材为,满足两个等式的数字是二元一次方程组的解.本质一样,但出发点不一样,表述各有特色.人教版教材方程内容中被定义的知识点个数要多于SM教材,比如对于二元一次方程组、三元一次方程组、一元二次方程、一元二次方程的解等概念的定义(教材中实际还有对一元一次方程、二元一次方程的定义),还有对代入消元法、加减消元法等解法的定义,而法国教材对这些没有提及.两个版本的教材对于基础知识点,比如方法的解释、运用,都较多涉及,体现了算法的思想.
对于两个国家的三个模块所出现的被定义的知识点个数如图1所示.
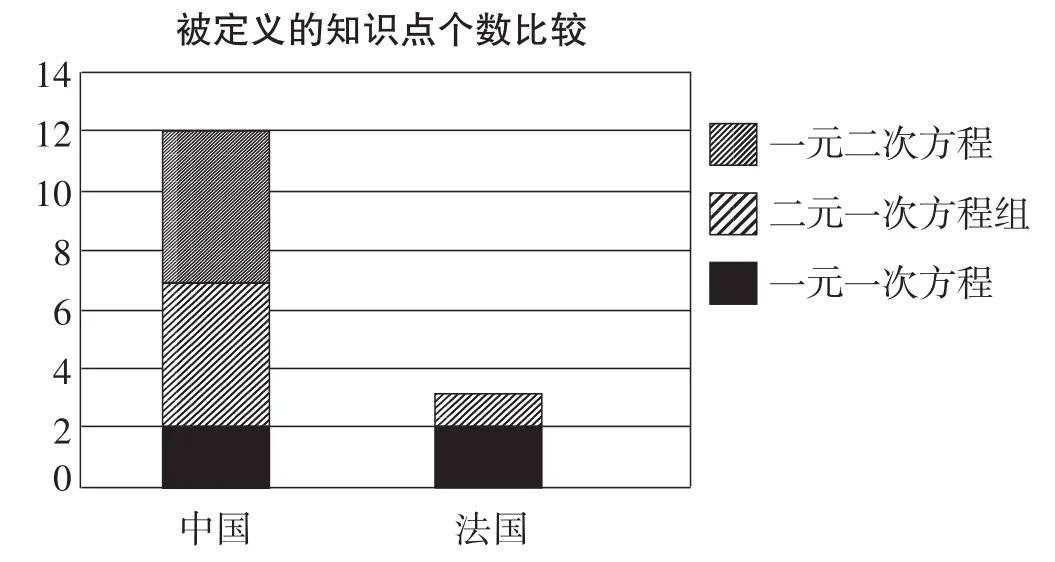
图1
从图1可以看出:人教版教材“方程”的三个模块被定义的知识点个数多于SM教材.
(2)内容深度比较.
将两个版本教材中方程三大模块的知识点按照内容深度指标表(见表2)进行汇总(一元一次方程的应用、二元一次方程组的应用、一元二次方程的应用三个知识点除外,不计入总数),并将两个指标不同水平的知识点个数进行统计,得到图2.

图2
由图2可知:两个版本的教材内容呈现方式都偏重于类比、归纳水平,且人教版教材的偏重更重,人教版教材三个水平差距大,SM教材三个水平差距小.
(3)例、习题比较.
将两个版本教材方程部分例、习题按照难度量化指标表(见表3)进行统计,得到表4.

表4:两个版本教材方程例、习题难度量化数据
①例题比较.
人教版教材中方程部分有22道例题,SM教材中方程内容有23道例题,根据上面公式计算难度获得其比较的三角形图,如图3所示.
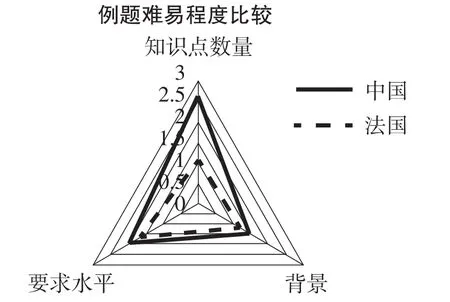
图3
②习题比较.
人教版教材中方程内容习题共167道,SM教材中方程内容部分习题共165道,两个版本教材习题数目不相上下,根据公式(1)计算难度获得其比较的三角形图,如图4所示.

图4
综上所述,SM教材中方程部分例、习题难度低于人教版教材中方程部分例、习题难度.
2.质性分析
(1)核心知识点的处理比较.
对于方程,两个版本教材的设置各有特点,特别是对核心知识点的处理,这点充分体现在知识点的引入上.现分别选取列方程(SM教材中没有该知识点,但有相关的解释)、方程的性质两个有代表性的知识点做比较,从而得出两个版本教材对方程核心知识点处理的不同.
①列方程的比较.
列方程在中国是一个基础知识点,同时也是一个教学难点,研究它的引入,并且对比它在SM教材的引入,是非常有意义的.在人教版教材中,给出列方程这个知识点之前,首先给出一个“汽车匀速经过三个村庄”的具体实例,题目给出了具体的解题步骤,同时设了好多空白,让学生自己试着在原有的知识基础上作答,然后拓展为列方程,从而完成了列方程的引入.
SM教材虽然也没有明确地提出列方程,但对于这个知识点,教材中还是以活动的形式给出了解释,这个活动有具体的步骤,见案例1.
案例1:(1)Alice用一个数乘以8,然后加上7,得到一个结果;(2)Bertrand用一个数乘以6,然后加上13,得到一个结果;(3)Chloe用一个数乘以3,然后加上30,得到一个结果;(4)如果Alice和Bertrand的起始数都是x,并且得到的结果是一样的,写出一个含有x的方程;如果Alice和Chloe的起始数字都是y,并且得到的结果是一样的,写出一个含有y的方程;如果Bertrand和Chloe的起始数字都是z,并且得到的结果是一样的,写出一个含有z的方程.
【评析】案例1的整个过程简单明了,每一步都让学生自我体验,逐步引导学生求知,从而列出方程.
②方程的性质的比较.
方程的性质在两个版本的教材中都有出现,它对解方程起着至关重要的作用,学生只有充分理解它的内涵,在应用时才能得心应手.方程的性质包含两条,人教版教材对于这两条的引入,是从学生熟悉的天平开始的,接着给出两条性质,是一个回顾和告诉的过程.
而SM教材在给出性质之前,会给出一个有具体步骤的活动,里面有若干个问题,大致步骤见案例2.
案例2:Ali和Sonia有相同个数的球.(1)如果你给了他们相同数目的球,那他们的球数还相同吗?(2)如果你从Ali那里拿走了一个球,那你该怎么做才能使他们的球数依旧相同?(3)Sonia在玩三倍于原来数目的球,那Ali是不是也得增加相同数目的球才能保持相等?(4)Ali给了别人他的原来一半的球,Sonia也这样做,那他们的球数还相同吗?(5)总结出一些性质.
【评析】案例2的每一步让学生设身处地思考,在这个基础上,再给出两条性质.很容易看出,SM教材把两条性质分成了四小条,前两小条对应性质1,后两小条对应性质2,注重各个击破.
(2)实际应用的比较.
两个版本教材都注重对三个模块的实际运用,特别是人教版教材,对于这三个部分的应用,还设立了独立的小节进行整体讨论探究,SM教材虽然没有作为独立的小节研究,但对应用的介绍还是很有特点的.例如,两个版本教材对于一元一次方程的应用的设置.人教版教材的一元一次方程的应用在章末的“实际问题与一元一次方程”小节中着重讨论,题目以探究题的形式出现.
探究:这是一个关于销售中的盈亏的具体问题:一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,那么这两件衣服总的是盈利还是亏损,或是不盈不亏?
给出题目后,先进行分析,然后设盈利25%的那件衣服的进价是x元,根据进价与利润的和就是售价,就可以得到方程x+0.25x=60,解得x=48.类似地,设另外一件衣服的进价,根据相等关系得到方程,进而求解,得到答案.然后结合两个答案,得到最终的答案.在这方面人教版教材注重知识的探究和拓展.
SM教材的一元一次方程的应用主要体现在对结果的解释上,如案例3.
案例3:问题1:Sylvia比他的妹妹Rose大7岁.10年之后,Sylvia的岁数比妹妹Rose大一倍.如果把Rose的年龄设为x,那么Rose多大了?
问题2:2000年,Paul的年龄是10岁,Louis的年龄是17岁,什么时候Louis的年龄是Paul的两倍?把这一年与2000年的差设为x.
(1)把这两个问题列成方程,你意识到了什么?
(2)解决这两个方程;
(3)把两个结果放在一起,进行总结.
【评析】根据问题1,可以列出方程:7+x+10= 2(x+10).解得x=-3;根据问题2,可以列出方程:17+x=2(x+10).解得x=-3.把两个方程放到一起,
很容易看出这两个方程是一样的,结果也一样.那么对于问题1,得到x=-3,意义就是Rose的年龄是-3岁;对于问题2,也得到x=-3,意义就是1997年,Louis的年龄是Paul的两倍.很显然,这两个结果不符合实际情况,故这两个解不成立,也就是说题目无解.这种逐步引导学生思考、发现,最后总结的活动步骤,在人教版教材中是没有出现的.
四、研究结论及启示
1.研究结论
(1)在内容广度上,人教版教材方程的内容广度比SM教材中方程的内容广度大,且三大模块定义的知识点个数明显多于SM教科书.
(2)在内容深度上,人教版教材三个模块的知识点的呈现方式都偏重于第二个水平,即归纳、类比.但人教版教材的偏重程度要高于SM教材,并且人教版教材三个水平差距大于SM教材.
(3)在例、习题难度上,人教版教材的三个难度因素水平都普遍高于SM教材.从难度取值来看,在背景方面,人教版教材题目比较关注学生的个人生活背景,SM教材更多的是无背景;在知识点数量上,人教版教材题目知识点含量明显高于SM教材,知识点含量差距大;在要求水平上,人教版教材略高于SM教材,都偏重于“理解”层次.
(4)在对核心知识点的处理、实际应用的比较上,人教版教材比较注重对知识的探索与拓展,注重对具体问题的解决;SM教材注重学生的自我体验和感悟,对知识点的各个击破,逐步引导学生求知.
2.启示
(1)注重基础.初中阶段属于义务教育阶段,以掌握基础知识、形成基本技能为主,重视通性、通法的掌握.两个版本教材的方程部分知识均以三大模块出现,即一元一次方程、二元一次方程组、一元二次方程,并且两个版本教材对于一些基础知识点都很注重.比如,方法的解释:解二元一次方程组中的代入消元法、加减消元法(在SM教材中,叫高斯消元法)、解一元二次方程中的配方法(在SM教材中,叫完全平方法)、因式分解法(在SM教材中,有提公因式法、平方差公式法)等;方法的运用:一元一次方程的运用、二元一次方程组的运用、一元二次方程的运用等;在例、习题方面,中法两国题目的内容设计也重在基础.
(2)适当减少“方程”的定义个数.有人做过统计,一本书中出现的定义个数与读完这本书的人成反比.方程这块知识在初中教材中的位置不容忽视,而且它的现实应用性也很高,但有时比较抽象,难以把握,出现较多的定义,不但达不到预期的教学目的,反而会让学生产生一种厌学心理.
(3)注重对知识各个击破,以及逐步引导学生求知.相比于算式,方程引入了未知数,是含有未知数的等式,建立的逻辑关系比较抽象,如果学生没有深入理解用方程解决问题的各个知识点的含义,就不能准确地用方程解决问题.SM教材的实际应用和对核心知识点的处理方面,设置的“活动”部分从每个知识点出发,逐步引导学生一一击破,使学生充分了解知识,理解并掌握它们.所以,注重对每个知识点的各个击破,逐步引导学生运用方程显得尤为重要.
[1]张奠宙.数学的明天[M].南宁:广西教育出版社,2000.
[2]姜美玲.教师实践性知识研究[M].上海:华东师范大学出版社,2008.
[3]人民教育出版社课程教材研究所中学数学课程教材研究开发中心.义务教育教科书·数学(七年级上册)[M].北京:人民教育出版社,2012.
[4]人民教育出版社课程教材研究所中学数学课程教材研究开发中心.义务教育教科书·数学(八年级上册)[M].北京:人民教育出版社,2012.
[5]人民教育出版社课程教材研究所中学数学课程教材研究开发中心.义务教育教科书·数学(九年级下册)[M].北京:人民教育出版社,2012.
[8]周九诗,王延文.中英初中数学教科书难易程度的比较研究:以中国“人教版”和英国《数学连接》为例[J].数学教育学报,2013,22(3):18-23.
[9]范良火,黄毅英,蔡金法,等.华人如何学习数学(中文版)[M].南京:江苏教育出版社,2005.
2016—07—19
河南省教师教育课程改革研究项目——多元化学习评价在高校数学类教师教育理论课程的实践与探索(2016-JSJYYB-012);河南大学民生学院教育教学改革研究项目——《概率论与数理统计》课程的学习成绩归因分析及对策研究(MS⁃JG2015025).
尚亚明(1991—),女,博士,主要从事数学教育方向的研究.
