多层回转体预紧结构层间转动试验
2016-12-07温金鹏廖晓雄万方美
温金鹏, 廖晓雄, 万方美, 薛 江, 李 斌, 杜 强
(1.中国工程物理研究院总体工程研究所 绵阳,621999) (2.西北工业大学航空学院 西安,710072)
多层回转体预紧结构层间转动试验
温金鹏1, 廖晓雄1, 万方美1, 薛 江1, 李 斌2, 杜 强1
(1.中国工程物理研究院总体工程研究所 绵阳,621999) (2.西北工业大学航空学院 西安,710072)
为研究含黏弹性材料多层回转体结构在轴向振动作用下的层间转动特性,设计了多层回转体试验件,进行了黏弹性材料压缩力学性能研究,建立了考虑黏弹性材料非线性力学特性的结构动力学模型。基于模态试验考察了不同预紧力条件下结构的模态变化规律,在此基础上开展了随机振动环境下试验件层间转动特性试验,获得了确定的层间转动现象,并研究了不同振动量级及预紧力对层间转动的影响。基于随机振动试验获得了含黏弹性材料回转体预紧结构层间转动与否的预紧力、振动量级分界线。相关试验结果可为工程设计提供支持。
预紧; 振动试验; 黏弹性材料; 层间转动; 回转体
引 言
在航空航天和汽车等领域中,有大量的由多层回转体零部件组成的组合结构。当这些回转体组合结构的零部件材料特性尤其是材料的线膨胀系数差异较大时,为了实现这些部件的有效连接,采用黏弹性材料作为组合回转体结构层间间隙的填充材料,通过压缩填充材料产生预紧力来实现对各层抱紧防松,保证产品在力学环境作用下各零部件的相对位置不变,降低产品在振动、冲击载荷作用下的力学响应,减小各部件因线膨胀系数差异和温度变化而产生的内应力,提高产品对外界力学环境和温度变化的适应能力。
多层回转体预紧组合结构一般是由两层以上球形或柱形回转体零部件及层间垫层组成。实际工程设计中,在受到其他设计要求约束的情况下,预紧力过大时,容易造成系统长期处于高应力状态,影响使用寿命;预紧力过小时,各层之间容易发生相对转动,影响其功能;因此需对多层回转体的动力学特性进行研究。目前,国内外学者主要从垫层材料的预紧量和材料非线性、激励外载及结构质量偏心等方面对多层回转体动态响应开展了相关工作。刘占芳等[1]基于垫层材料的黏弹性本构关系研究了周期载荷激励下预紧量、黏性因素以及激励外载对结构动力学特性的影响。郭然等[2]基于直接约束模型,选用库伦摩擦模型模拟摩擦力,对三层壳体在集中力作用下的应力和变形状态进行了数值分析。肖世富等[3]考虑预紧偏心垫层结构的内层转动及层间相对滑移,分析了预紧垫层结构的动力学现象及系统对初值的敏感性,给出了不同偏心量系统层间转动滑移平衡解的概率分布。文献[4-6]分别采用有限元方法、分层理论和波传播法研究了带约束黏弹性夹层的圆柱壳振动响应特性。Piskunov等[7]通过将厚圆柱壳沿厚度方向分为一系列薄壳,对长厚比小于5的柱壳结构的动力学特性进行了分析。
在层间转动方面,许茂[8]建立了预紧接触式垫层结构的非线性数学模型,结合试验研究探索了层间滑移的机理。王江[9]基于多孔硅橡胶垫层材料,提出超弹性和有限变形黏弹性本构模型,分析了各部件之间接触状态与外界载荷之间的关系。王飞等[10]基于Mooney-Rivilin超弹性本构模型,采用Abaqus对振动环境下的多层回转体预紧结构进行分析,从运动学角度定义了最小滑移偏移距作为预紧防转的判据,建立了防转有效性的分析方法。Thomsen等[11]针对经典的质量块-传送带模型,推导了考虑振幅、频率的黏滞-滑移和纯滑移的解析模型。Baets等[12]通过试验验证了相对加速度导致黏滞-滑移运动的机理模型。
对于多层回转体预紧结构,当预紧力不同时其结构刚度不同,结构的动力学特性也将发生变化,而现有的理论分析手段难以定量分析多层回转结构在振动环境下的转动现象。为了研究不同预紧力下的结构层间转动特性,笔者设计了能对预紧力连续调节的多层回转体振动试验装置,建立了考虑黏弹性材料非线性力学特性的结构动力学模型,开展了不同预紧力下结构模态特性的试验研究。通过不同振动量级下结构的层间转动试验,分析了预紧力层间转动特性的影响规律,在此基础上给出了含黏弹性材料回转体结构不发生层间转动的预紧力、振动量级包络线。研究结果为含黏弹性材料多层回转体预紧结构层间防转设计提供技术支持。
1 试验件设计
为研究含黏弹性材料多层回转体在轴向振动载荷下的层间相对滑移转动,同时避免结构偏心对层间转动的影响,设计了如图1所示的含黏弹性材料回转体试验件。该试验件由上下壳体、内层壳体、黏弹性材料(硅泡沫垫层)、加载螺母和力传感器组成。其中,硅泡沫垫层裱糊在上下壳体与内层壳体之间。试验件通过旋紧加载螺母压缩垫层产生预紧力,并根据试验需求对预紧力大小进行任意调节,预紧力的大小通过力传感器直接读取。进行振动试验时,试验件通过下壳体固定螺栓与振动台面联接,在振动载荷作用下上下壳体与内层壳体之间产生以轴线为中心的相对滑移与转动。
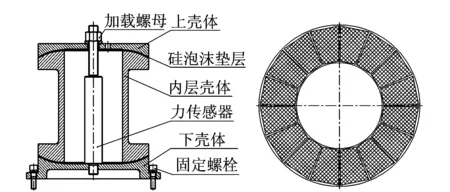
图1 轴向振动试验件及垫层裱糊形式Fig.1 The axial vibration specimen and cushion layer pasting form
2 黏弹性材料压缩力学性能
多层回转体层间的黏弹性材料由硅泡沫材料与胶层组成,如图2所示。在多层回转体预紧结构的使用过程中,处于内、外壳体之间的黏弹性材料总处于受压状态,即垫层在工作环境中沿厚度方向存在预紧力。预紧力的大小直接影响多层回转体结构的动态特性以及层间是否会发生相对转动。因此,掌握垫层材料的静态压缩性能对多层回转体预紧结构动态防转性能的分析评估具有重要意义。

图2 垫层组成Fig.2 The constitute of cushion layer
从厚度为0.75 mm的垫层上取样,在材料实验机上对试样进行压缩,试样压缩应力-应变曲线如图3所示。可以看出,硅泡沫材料的压缩力学性能呈现3个不同的阶段:①为弹性变形区,该阶段主要是由胞壁的弹性变形引起的;②为应力平台区,该阶段随着压缩量的增加,泡孔内气体扩散逸出,导致胞壁屈曲和局部胞壁的坍塌,相应的应力增长较慢;③为坍塌致密区,主要是硅泡沫泡孔的整体坍塌引起,并导致压缩模量的急剧增大。硅泡沫垫层的应力平台区的应变约为10%~35%,是进行结构设计时较为理想的应变分布区域。
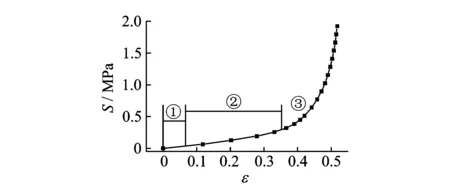
图3 硅泡沫垫层材料压缩应力-应变曲线Fig.3 The stress-strain curve of silicon foam cushion material
3 轴向振动试验件动力学分析
将轴向振动试验件离散为质量-弹簧系统,简化后结构的动力学模型如图4所示。由于上下壳体及内层壳体的质量、弹性模量相对于垫层大得多,故将上下壳体及内层壳体简化为刚性的质量元件,并将垫层的质量分布到内层壳体上。

图4 质量弹簧阻尼系统Fig.4 The mass-spring-damping system
由图3垫层的应力-应变曲线可知,在线弹性区及平台区,垫层材料可近似简化为线性弹簧;在密实区,垫层材料存在很强的非线性,所以其弹性恢复力整体是非线性的,记为Fk。系统由于包含界面处的干摩擦阻尼、黏弹性材料而存在诸如材料阻尼、层间滑移或转动产生的滑移阻尼等多种阻尼,其阻尼力也是非线性的,记为Fc。假设弹性恢复力和阻尼力不存在耦合关系,且垫层不发生分离,则系统的弹性恢复力为
(1)
由对称性可知另一边的弹性恢复力为
(2)
总的弹性恢复力为
(3)
其中:K为系统的刚度阵;x为内层壳体的振幅;Δ为垫层的预紧量;βi为幂函数多项式系数。
只考虑系统的干摩擦阻尼时,系统阻尼可表示为振幅A、频率f及预紧量Δ的关系式
(4)
其中:γ,l均为比例系数。
由达朗贝尔原理可得系统的动力学方程为
(5)
将式(3),(4)代入式(5),得到
Δ)2i-1+(x-Δ)2i-1]=F(t)
(6)
其中:M为系统的质量阵;F(t)为系统承受的外激励力。
当垫层处于线弹性区及平台区时,弹性恢复力可近似简化为线性,式(6)可简化为
(7)
取F(t)=P0sin(ωt)可以解得系统的稳态响应幅值为
(8)

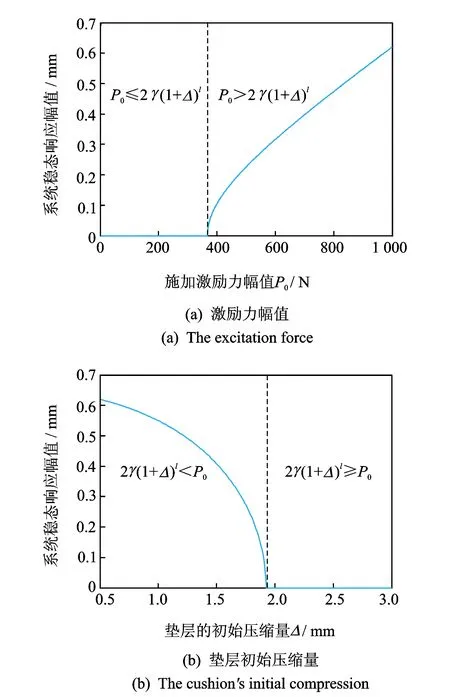
图5 激励力幅值、垫层初始压缩量对系统稳态响应的影响Fig.5 The influence of excitation force and cushion′s initial compression on system response
对式(8)化简,得到系统的稳态响应幅值为
(9)
由式(9)可知,在垫层的初始压缩量一定的情况下,当激励力的幅值P0≤2γ(1+Δ)l时,系统的稳态幅值为零。只有当激励力的幅值满足P0>2γ(1+Δ)l时,振动才能继续。激励力的幅值对稳态响应幅值的影响如图5(a)所示,当激励力幅值大于临界值时,系统稳态响应随着激励力幅值的增大而呈非线性的增加;当激励力幅值很大时,系统稳态响应的幅值与激励力的幅值几乎呈线性增大。
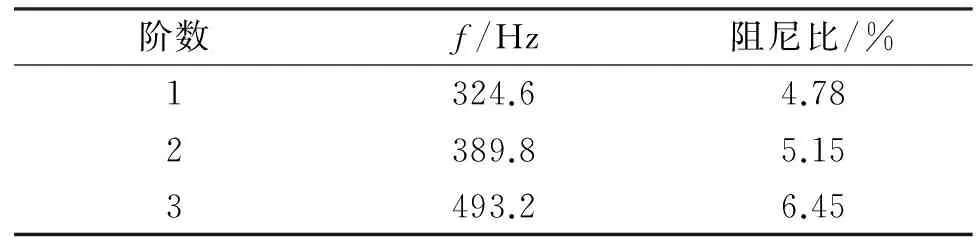
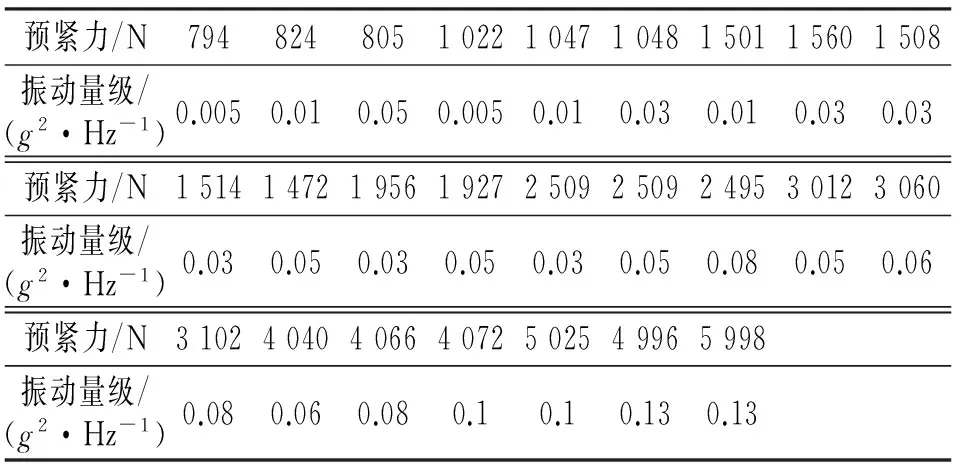
由式(9)可知,在系统的激励力确定的情况下,如果垫层的初始压缩量使得2γ(1+Δ)l≥P0时,系统的稳态幅值为零。只有当垫层的初始压缩量满足2γ(1+Δ)l 为研究预紧力对模态参数的影响,对轴向振动试验件开展了不同预紧力条件下的模态测试分析。试验采用自由支撑方式(即用柔性绳吊起),通过激振器对试验件进行激励,如图6所示。 图6 模态试验激励方式及测点布局Fig.6 The exciting mode and measuring points of the modal test 整体模态试验装配预紧力松弛稳定后为1 007 N,试验采用激振器施加单点随机激励信号,对所有测点的切向及径向加速度响应进行测量。图7与图8分别为激励信号的频响函数和前三阶模态振型。预紧力为1 007 N时结构前三阶模态试验结果如表1所示。 图7 激振点频响函数Fig.7 The FRF at the location of the force excitation Tab.1 The modal test results of the specimen with the pre-tightened load 1 007 N 阶数f/Hz阻尼比/%1324.64.782389.85.153493.26.45 图8 前三阶模态振型图Fig.8 The first three order vibration modes 由表1与图7~8可得:整体结构的前三阶模态分别为上下壳体相对于内层壳体的同向转动、相互错动及反向转动,基本不存在耦合现象,同时结构的前三阶模态阻尼均比较大。以试验件的一阶频率为特征参数,研究其随预紧力的变化规律。 进行多种预紧力条件下的频响函数测试,参数如表2所示。当预紧力从1 007 N增加到6 926 N时,垫层应力从0.051 MPa增加到0.348 MPa,由图3可知均处于垫层材料的线弹性区与平台区。通过重复性测试表明:试验在保持一定预紧力及激励幅值的条件下,所有测点的频响函数重复性较好;测试过程中结构预紧力基本保持恒定。 表2 不同装配预紧力结构一阶频率试验结果 Tab.2 The first-order natural frequency with different pre-tightened loads 试验前预紧力/N垫层应力/MPa一阶频率/Hz试验前预紧力/N垫层应力/MPa一阶频率/Hz10070.051324.619000.095368.7531260.157431.2540160.202482.548530.244547.560780.305613.7569260.348641.25 基于不同装配预紧力,对结构全部测点的频响函数进行平均,如图9所示(预紧力从1 007 N逐渐增至6 926 N)。结构一阶频率随装配预紧力的变化如图10及表2所示。试验结果表明,结构的一阶频率与预紧力呈正比关系。原因是在垫层压缩性能的线弹性区与平台区,预紧力的增加引起垫层扭转刚度变大,导致结构整体刚度变大;模态频率与结构刚度的平方根呈正比关系,因此预紧力的增加必然导致模态频率的增大。 图9 不同预紧力结构频响函数Fig.9 The FRF with different pre-tightened loads 图10 一阶频率与预紧力关系拟合曲线Fig.10 The fitted curve of the first order natural frequency with pre-tightened loads 模态试验结果表明,含黏弹性材料回转体结构的预紧力不同,其模态也有相应改变,同时结构的低阶模态振型表现为层间相对滑移或转动。为分析振动环境下结构的层间转动行为,开展了结构在不同预紧力、不同振动量级条件下的动力学试验。 图11 振动试验系统及装置Fig.11 The vibration experiment system and apparatus 轴向振动试验系统如图11所示,试验件通过下壳体固定螺栓与振动台面固连,试验采用下壳体上的加速度响应信号进行四点平均控制。同时采用图12所示的功率谱密度曲线进行振动试验,依据试验情况对G值进行动态调整。试验时通过在结构的上、下壳体与内层壳体之间粘贴刻度纸对结构的转动行为进行监测,每个试验工况持续时间为300 s。不同预紧力与振动量级的试验工况如表3所示,共25种工况。 图12 随机振动功率谱密度谱形图Fig.12 The power spectral density of random vibration 预紧力/N794824805102210471048150115601508振动量级/(g2·Hz-1)0.0050.010.050.0050.010.030.010.030.03预紧力/N151414721956192725092509249530123060振动量级/(g2·Hz-1)0.030.050.030.050.030.050.080.050.06预紧力/N3102404040664072502549965998振动量级/(g2·Hz-1)0.080.060.080.10.10.130.13 不同工况随机振动试验结果如图13所示。可见,当振动量级相对较低时,较小的预紧力即可防止结构发生层间转动,确保结构各层位置不变。如振动量级为0.01g2/Hz时,预紧力为1 kN,振动试验过程中结构未发生层间转动。随着振动量级的升高,防止结构发生层间转动的预紧力也相应增大,当振动量级升至0.06g2/Hz时,预紧力需增大至4 kN才能保证结构不发生层间转动。试验研究表明,为确保常规的振动量级(0.13g2/Hz以下)结构不发生转动时,预紧力需增大至6 kN以上;同时试验过程中转动量与预紧力、振动量级之间的关系呈现随机分布,难以量化。 图13 不同工况结构随机振动试验结果Fig.13 The vibration experiment results with different conditions 为确保轴向振动试验件不发生层间转动,需从预紧力和振动量级两方面采取措施。振动量级相同条件下,增大预紧力可有效防止结构发生层间转动。降低振动量级,则防止相对转动所需的预紧力减小。可见,增大预紧力,减小振动量级均有利于防止试验件发生层间转动。 当试验件长时间放置后,由于黏弹性材料的松弛效应,在压缩量不变的条件下,预紧力将会下降。对于相同振动量级,试验件相对转动的趋势将会增加。因此在实际应用中,对结构预紧力开展设计时需考虑黏弹性材料的松弛效应。 基于振动试验的预紧防转有效性判定,是所有判定方法中最直接的手段。通过轴向振动试验件随机振动试验结果(见图13)的分析,构建层间转动与预紧力、振动量级的关系,如图14所示。其中,结构产生转动、未转动的工况分别用三角形和正方形表示。由图14可知,预紧力与振动量级之间可能存在结构转动区与未转动区的分界线。基于试验结果,选取未转动区域与转动区域之间的未转数据点进行曲线拟合,建立拟合分界线。 图14 预紧力、振动量级与结构转动之间的关系Fig.14 The relationship between interlayer rotation of cylindrical structure and pre-tightened load, vibration magnitude 拟合分界线上的预紧力与振动量级之间关系定义为 A=m+bF (10) 其中:A为振动量级;F为装配预紧力;m,b为拟合因子。 预紧力与振动量级的函数关系式为 A=-0.016+2.36×10-5F (11) 由图14可得,拟合分界线的上方为结构发生转动的区域;拟合分界线及其下方为结构未发生转动的区域;同时有4个结构未发生转动的数据点不在拟合分界线下方。结果表明,拟合分界线不能准确区分转动与未转动区域,但可为确定结构不发生转动的预紧力、振动量级范围提供技术支撑。 1) 依据含黏弹性材料回转体预紧结构的动态特性,设计了含黏弹性材料多层回转体试验件,并对黏弹性材料进行了压缩性能测试,建立了考虑黏弹性材料非线性力学特性的结构动力学模型。在此基础上,通过试验开展多层回转体的模态分析,得出了在一定预紧力范围内多层回转体结构一阶模态频率与预紧力呈正比关系。 2) 开展了多层回转体预紧结构振动试验,试验结果表明,增大预紧力和减小振动量级均有利于防止试验件发生层间转动。基于试验数据,拟合得到了结构层间转动发生与否的预紧力、振动量级分界线的函数关系式。该研究可为工程上多层回转壳预紧结构初始预紧力的制定提供支持。 [1] 刘占芳,王江,张华.带预紧硅泡沫垫层减振结构的动力特性[J].中国工程机械,2007,18(14):1668-1672. Liu Zhanfang, Wang Jiang, Zhang Hua. Dynamics property of structure with pre-tightening silicone rubber cushion[J]. China Mechanical Engineering, 2007,18(14):1668-1672. (in Chinese) [2] 郭然,施惠基,郁向东.多层圆柱结构接触预紧力失效分析[J].工程力学,2003,20(4):192-198. Guo Ran, Shi Huiji, Yu Xiangdong. Failure analysis of the multi-layer cylindrical structure by pre-stressed contact load[J]. Engineering Mechanics, 2003,20(4):192-198. (in Chinese) [3] 肖世富,沈展鹏,陈学前,等.一类预紧偏心垫层结构的动态特性与稳定性分析[J].中国机械工程,2012,23(10):2290-2296. Xiao Shifu, Shen Zhanpeng, Chen Xueqian, et al. Study on dynamic behavior and stability of an eccentric pretightened cushion structure[J]. China Mechanical Engineering, 2012,23(10):2290-2296. (in Chinese) [4] Farough M, Ramin S. Linear and nonlinear vibration analysis of sandwich cylindrical shell with constrained viscoelastic core layer[J]. International Journal of Mechanical Sciences, 2012,54:156-171. [5] Wang Hongjou, Chen Lienwen. Finite element dynamic analysis of orthotropic cylindrical shells with a constrained damping layer[J]. Finite Elements in Analysis and Design, 2004,40:737-755. [6] Cao Xiongtao, Zhang Zhiyi, Hua Hongxing. Free vibration of circular cylindrical shell with constrained layer damping[J]. Applied Mathematics and Mechanics, 2011,32(4):495-506. [7] Piskunov V G, Marchuk A V, Ya L. Free vibrations of thick layered cylindrical shells[J]. Mechanics of Composite Materials, 2011,47(2):177-184. [8] 许茂.预紧接触式垫层结构的动力学分析[D].绵阳:中国工程物理研究院,2003. [9] 王江.带预紧硅泡沫垫层结构的减振系统分析[D].重庆:重庆大学,2008. [10]王飞,庄茁,万方美,等.振动环境下过盈装配圆柱结构预紧防转判据研究[J].振动与冲击,2015,34(8):187-192. Wang Fei, Zhuang Zhuo, Wan Fangmei, et al. Interference preload anti-rotation validity criterion for cylinder assemblies under vibration environment[J]. Journal of Vibration and Shock, 2015,34(8):187-192. (in Chinese) [11]Thomsen J J, Alexander F. Analytical approximations for stick-slip vibration amplitudes[J]. International Journal of Non-Linear Mechanics, 2003,38:389-403. [12]Baets P D, Degrieck J, Van De Velde F, et al. Experimental verification of the mechanisms causing stick-slip motion originating from relative deceleration[J]. Wear, 2000,243:48-59. 10.16450/j.cnki.issn.1004-6801.2016.04.026 国家自然科学基金青年基金资助项目(11302207);中央高校基本科研业务费专项资金资助项目(3102014KYJD015) 2015-06-13; 2015-12-29 TH113; TB123 温金鹏,男,1985年1月生,博士、副研究员。主要研究方向为结构动力学与动态破坏分析。曾发表《Study on cushioning characteristics of soft landing airbag with elastic fabric》(《International Journal of Applied Electromagnetics and Mechanics》2010,Vol.33,No.3-4)等论文。 E-mail:401wenjp@caep.cn 简介:廖晓雄,男,1978年5月生,硕士、高级工程师。主要研究方向为机械结构设计与可靠性。 E-mail:liaoxx@caep.cn4 轴向振动试验件模态分析
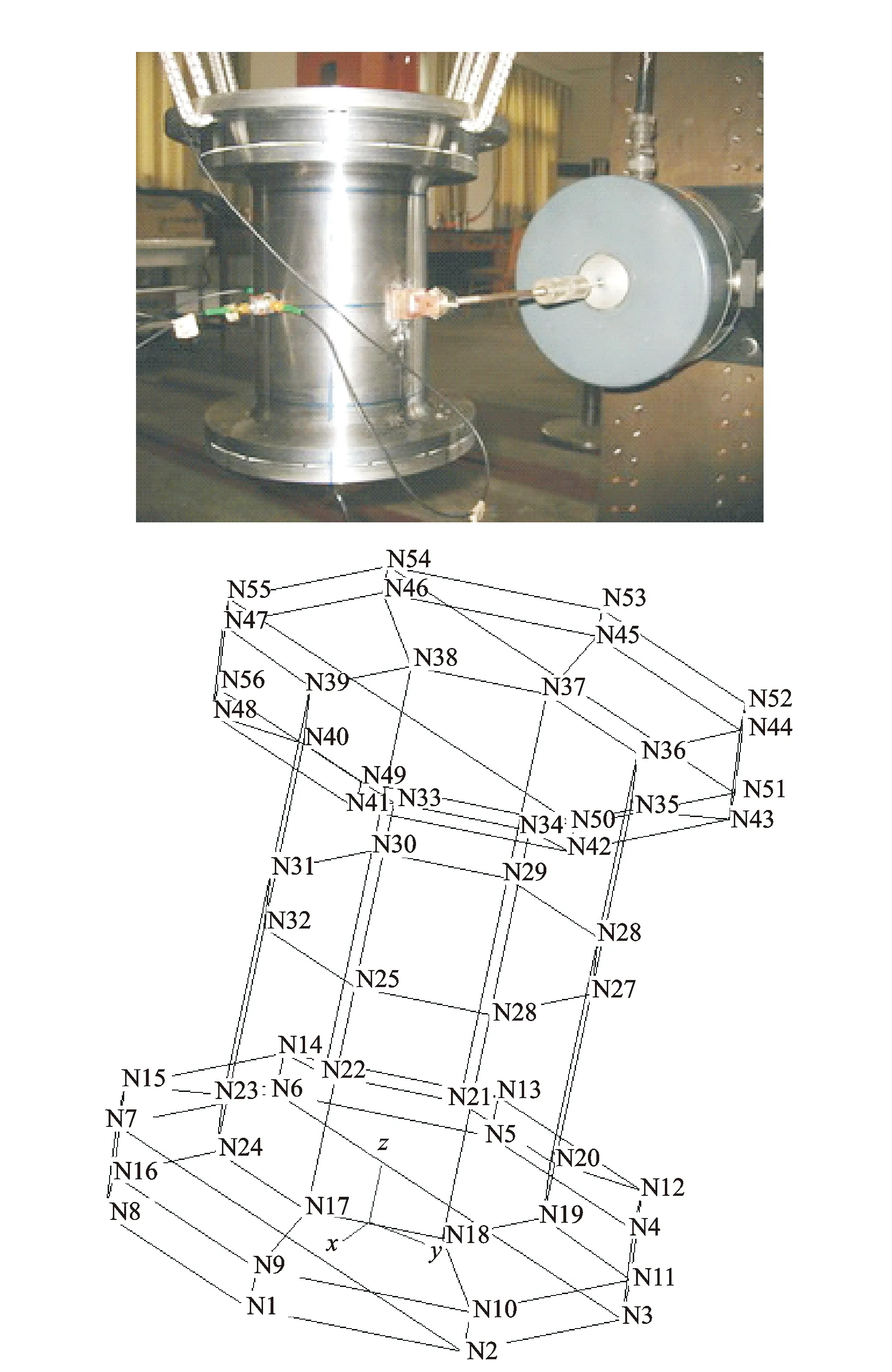




5 轴向振动层间转动试验系统


6 试验数据分析

7 预紧防转有效性判定

8 结 论

