行星减速器驱动旋转双柔性梁T-S模糊振动控制

邱志成， 吴传健

(华南理工大学机械与汽车工程学院 广州，510640)



行星减速器驱动旋转双柔性梁T-S模糊振动控制

邱志成， 吴传健

(华南理工大学机械与汽车工程学院 广州，510640)

旋转双臂的柔性结构在转动调姿时或外部扰动的影响下产生振动，将影响系统的稳定性和定位精度,减速器间隙非线性影响旋转双柔性梁结构的动态特性，加大了控制难度。研究了一种多变量非线性T-S模糊(nonlinear T-S fuzzy, 简称NTS)控制算法，利用模糊控制器的多变量解耦控制能力以及T-S模糊规则具有的分段控制特点快速抑制柔性结构小幅值振动。设计并建立了交流伺服电机通过行星减速器驱动转动的双柔性压电梁结构实验平台。利用压电传感器采集振动信号，压电驱动器和交流伺服电机驱动器抑制柔性结构振动，对该控制方法进行实验研究。实验结果表明，相对于比例加微分(proportional and derivative, 简称PD)控制算法，非线性T-S模糊控制算法对于系统的大幅值振动和小幅值振动都有较快速的振动抑制效果。

旋转双柔性梁； 振动控制； T-S模糊控制； 行星减速器； 间隙； 耦合

引 言

航天器太阳能帆板、空间柔性机器人以及螺旋桨等旋转柔性双臂结构，由于其柔性臂具有跨度大、质量轻、刚度低和阻尼小的结构特点[1]，使得在转动调姿时或者外部扰动下易产生持续振动，尤其在平衡点处小幅值的低阶固有频率振动很难被抑制。对于旋转机构而言，振动将影响其定位精度、缩短结构的使用寿命[2]，甚至造成系统不稳定。因此，对旋转柔性结构振动控制的研究具有重要意义。单悬臂柔性梁和旋转单柔性梁结构的振动控制研究已有大量成果[3-4]，已经实现了单悬臂柔性梁的振动控制、旋转单柔性臂振动的定点控制和轨迹跟踪控制。控制算法涉及非线性控制、模糊控制、神经网络控制、解耦控制、最优控制和时滞控制等。柔性结构振动控制采用的驱动器涉及压电陶瓷驱动器[5]、伺服电机驱动器和形状记忆合金丝驱动器等。

苏文敬等[6]建立了空间柔性双臂机器人的动力学模型，结合逆动力学控制算法实现了机器人的仿真控制。文献[7]基于奇异摄动理论，将带有柔性自由悬浮关节的空间机器人臂系统划分为慢速子系统和柔性关节快速子系统，实现了机器人臂振动的自适应控制。李祖枢等[8]分析了双柔性摆机器人的一个自稳定和3个自不稳定的平衡状态。通过将4个状态转化为12个相互转换的运动动作和8个自旋动作，建立对应的强耦合、非线性、多变量系统模型，并设计了多模态控制器，实现了实时控制。现有研究主要集中在双摆多级系统的动力学建模、稳定性控制和运动控制上，对旋转双柔性梁结构存在减速器间隙情况下的振动控制问题研究甚少。

旋转机构中采用的行星减速器在设计精度不高或长期磨损的情况下易产生齿轮间隙，齿轮间隙非线性在旋转单悬臂梁控制系统中表现为驱动死区、迟滞和极限环振荡等现象[9]。同时，减速器的摩擦特性将影响系统输入输出的线性关系。除了以上现象，还表现为双柔性梁之间的强耦合作用。这些不确定因素将降低控制器控制效果，甚至导致系统失稳。针对驱动器的间隙非线性和摩擦非线性，Campos等[10]运用神经网络辨识间隙模型，构造间隙反模型用于间隙的控制量在线补偿。Wang等[11]以具有摩擦非线性和间隙非线性的伺服电机-减速器驱动系统为研究对象，利用特征建模法描述系统不确定性和非线性，实现了系统的二阶滑模自适应跟踪控制。针对多变量系统的耦合问题，Tien等[12]将用于表示系统模型的耦合质量矩阵和刚度矩阵进行了对角化，实现了七自由度关节机器人的解耦控制。

行星减速器的摩擦非线性和间隙非线性、双柔性梁之间的强耦合作用，使系统精确模型难以获得，基于模型的线性算法控制效果不佳,因此有必要采用非线性解耦控制算法进行控制。文献[13]证明了模糊控制器在控制系统模型未知的情况下依然具有优良的控制效果。模糊控制器具有解耦特性[14]，便于多变量系统的控制器解耦设计。采用T-S模糊控制时，合理选择模糊规则可使控制器取得很好的控制效果，但模糊控制器的模糊规则很大程度上依赖设计者对受控系统的了解，即专家知识。因此，需要一个准则为模糊控制器的设计提供指导。

笔者针对目前研究存在的难点，首先介绍旋转双柔性梁实验平台的原理，分析双柔性梁结构的振动特性，提出梁的两种主要振动形态：同相振动和反相振动;其次，针对旋转双柔性梁结构，研究基于多输入多输出(multiple-input multiple-output, 简称MIMO)系统的非线性T-S模糊控制算法;最后，搭建实验平台，分别用PD控制算法和非线性T-S模糊控制算法进行实验比较。

1 旋转双柔性梁结构振动特性分析

1.1 实验系统描述

图1为旋转双柔性压电梁实验系统的原理图。梁Ⅰ和梁Ⅱ通过轮毂固定在行星减速器的输出轴上，使其可以在水平面内绕输出轴旋转。梁Ⅰ和梁Ⅱ上粘贴压电传感器和压电驱动器，分别用于采集梁的振动信号和抑制梁的振动。压电传感器Ⅰ和压电传感器Ⅱ采集到的振动信号经过电荷放大器放大后，通过端子板的A/D转换模块转为数字量，再经过运动控制卡输入计算机。交流伺服电机内部的编码器检测行星齿轮输入轴的转动角位移和角速度值，经过端子板和运动控制卡传输至计算机。振动信号和速度信号经由计算机的控制算法转换为控制量。其中，伺服电机的控制量由端子板的D/A转换模块和伺服输出，驱动器驱动伺服电机旋转。压电驱动器Ⅰ和压电驱动器Ⅱ的控制量由端子板的D/A转换模块输出，经由电压放大电路施加于梁Ⅰ和梁Ⅱ上，用于抑制柔性梁的振动。由于柔性悬臂梁根部位置的应变最大，将压电传感器器Ⅰ和Ⅱ、压电驱动器Ⅰ和Ⅱ双面粘贴在双梁的根部，压电驱动力在振动控制过程中可以得到较大程度的利用[15]。

图1 实验平台原理图Fig.1 Schematic diagram of experimental platform

1.2 行星减速器非线性对旋转双柔性梁振动特性的影响

图2为行星减速器间隙影响下的系统控制框图。图中：yr，e，u，d，kb，x和y分别为参考输入、振动误差、电机控制量、单侧间隙宽度、减速器减速比、减速器输出和采集到的输出量。由图中的间隙非线性简化模型可知，间隙模型的输出不仅与输入的大小有关，还与当前时刻输入的正负以及前一时刻的输入有关[16]。实际控制系统中的间隙非线性更加复杂，齿轮间隙特性对整个系统的影响表现为驱动死区和滞后、系统极限环振荡、驱动冲击和噪声干扰。对于旋转双柔性梁结构，齿轮间隙的存在使其中一梁的振动通过带动轮毂转动传递给另一个梁，即双柔性梁之间的耦合作用。当双柔性梁处于小幅值振动时，减速器输出轴近乎处于漂浮状态，此时只受到摩擦力的影响，双柔性梁表现出与大幅值振动时不同的振动特性。

图2 行星减速器间隙影响下的系统控制框图Fig.2 Schematic diagram of control system under the influence of planetary reducer backlash

行星减速器存在齿轮间隙时，双梁的耦合作用在定点振动情况下表现为反相振动形式，即梁Ⅰ和梁Ⅱ的振动方向绕输出中心轴的转动方向相反。当伺服电机控制其中一个梁时，另一个梁将会发散，此时系统不可控。笔者主要针对双梁的反相振动形式设计控制器。可见，行星减速器的间隙非线性和摩擦非线性增加了系统的不确定性。双梁的反相振动在伺服电机单独作用下具有不可控性，加大了结构的控制难度。

2 非线性T-S模糊控制器设计

2.1 模糊控制器结构的确定

旋转双柔性梁结构是一个强耦合、非线性MIMO系统。行星减速器齿轮间隙导致伺服电机驱动减速器旋转时进入控制死区，因此有必要在控制算法中引入非线性，利用压电驱动器快速抑制小幅值振动。伺服电机对于梁的驱动力相较压电驱动器更大，可采用伺服电机快速抑制大幅值振动。综合控制器性能要求，可先设计T-S模糊控制器对多变量系统进行控制器设计的解耦，再利用T-S模糊规则的分段性在控制器中引入非线性特性，实现小幅值振动的快速抑制。

图3 MIMO系统非线性T-S模糊控制原理框图Fig.3 Schematic diagram of Nonlinear T-S fuzzy controller for MIMO system

2.2 T-S模糊控制器的语言值和隶属度函数

模糊控制器的模糊语言值为{PB，PM，PS，ZO，NS，NM，NB}，分别表示“正大”、“正中”、“正小”、“零”、“负小”、“负中”和“负大”7个模糊子集。将这些语言值分别用{-3，-2，-1，0，1，2，}7个整数来表示。

考虑到高斯隶属度函数形式简单，易于计算机编程和调整形状的特点， T-S模糊控制器Ⅰ和Ⅱ均选用高斯隶属度函数。其数学表达式[17]为

(1)

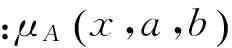
非线性T-S模糊控制器Ⅰ和Ⅱ的隶属度函数如图4所示。

图4 T-S模糊控制器Ⅰ和Ⅱ的隶属度函数Fig.4 Membership function of T-S fuzzy controller Ⅰ and Ⅱ

2.3 模糊推理规则设计

对于多规则的模糊推理问题，每一个规则都产生一个推理结果。最终的结论通过对每一个推理结果进行加权平均得到，即

采用单点模糊化、乘积推理法和中心加权平均解模糊化方法可求得T-S模糊逻辑系统的输出[18]为

(2)

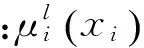
(3)

其中

压电驱动器Ⅱ的加权系数v和交流伺服电机对应的加权系数λ分别为

(4)

(5)

其中

权系数w和v的选取应确保小幅值处具有相对更大的控制增益，权系数λ的选取应确保电机对大幅值振动的控制效果。显然，非线性T-S模糊控制率是基于T-S模糊模型的非线性算法，对于单条规则，输入和输出呈线性关系。但是随着输入量的不断变化，模糊控制器内部参数不同程度地被激发，控制器的输出是输入信号的非线性加权叠加。另一方面，T-S模糊控制器实现了振动信号振动一个周期内非线性映射的同时，也实现了整个振动衰减过程的非线性映射，即T-S模糊控制率的分段性。

3 旋转双柔性梁结构振动控制实验

3.1 实验装置

本实验装置如图5所示。压电柔性梁Ⅰ和压电柔性梁Ⅱ采用环氧树脂材料。电机采用三菱公司生产的型号为HC-KFS43的交流伺服电机，功率为400 W。编码器的分辨率为40 000脉冲/转。伺服驱动器型号为MR-J2S-40A。行星减速器型号为VRSF-25C-400，减速比为1∶25，齿轮间隙为15角分。采样周期为2 ms。控制算法通过C++语言编程实现。压电传感器Ⅰ和Ⅱ电荷放大型号为YE5850。设定电荷放大器Ⅰ的灵敏度为99.9pC/Unit，输出档位1 mV/Unit。电荷放大器Ⅱ的灵敏度为10 pC/Unit，输出档位1 mV/Unit。将压电陶瓷产生的电荷放大至-10 V～+10 V的电压范围。研制的电压驱动电路将-5 V～+5 V的输入电压转换为-155 V～+155 V的输出电压。数据采集和转换采用型号为GTS-400-PGV的运动控制卡，输出电压范围和输入范围均为-10 V～+10 V。

图5 旋转双柔性压电梁实验装置Fig.5 Experimental setup of the rotating double flexible piezoelectric beams

实验平台主要尺寸如下：柔性梁Ⅰ为590 mm×98 mm×2.08 mm；柔性梁Ⅱ为600 mm×98 mm×2.08 mm；压电传感器Ⅰ为20 mm×6 mm×1 mm；压电传感器Ⅱ为40 mm×10 mm×1 mm；压电驱动器Ⅰ为50 mm×15 mm×1 mm；压电驱动器Ⅱ为50 mm×15 mm×1 mm。

3.2 实验结果与比较

3.2.1 双柔性梁自由振动实验

通过实验分别采集柔性梁Ⅰ和柔性梁Ⅱ的自由振动曲线如图6所示。自由振动曲线的激励方式为：用手拨动梁Ⅰ，待双柔性梁的振动幅值衰减接近10V时开始采样。梁Ⅰ的1阶固有频率为3.375 Hz，梁Ⅱ的1阶固有频率为3.4 Hz。梁Ⅰ经过4.5 s衰减至50%，经过13.5 s衰减至10%；梁Ⅱ经过4.2 s衰减至50%，经过14.2 s衰减至10%。实验数据显示，梁Ⅰ和梁Ⅱ的小幅值振动衰减需要较长时间。

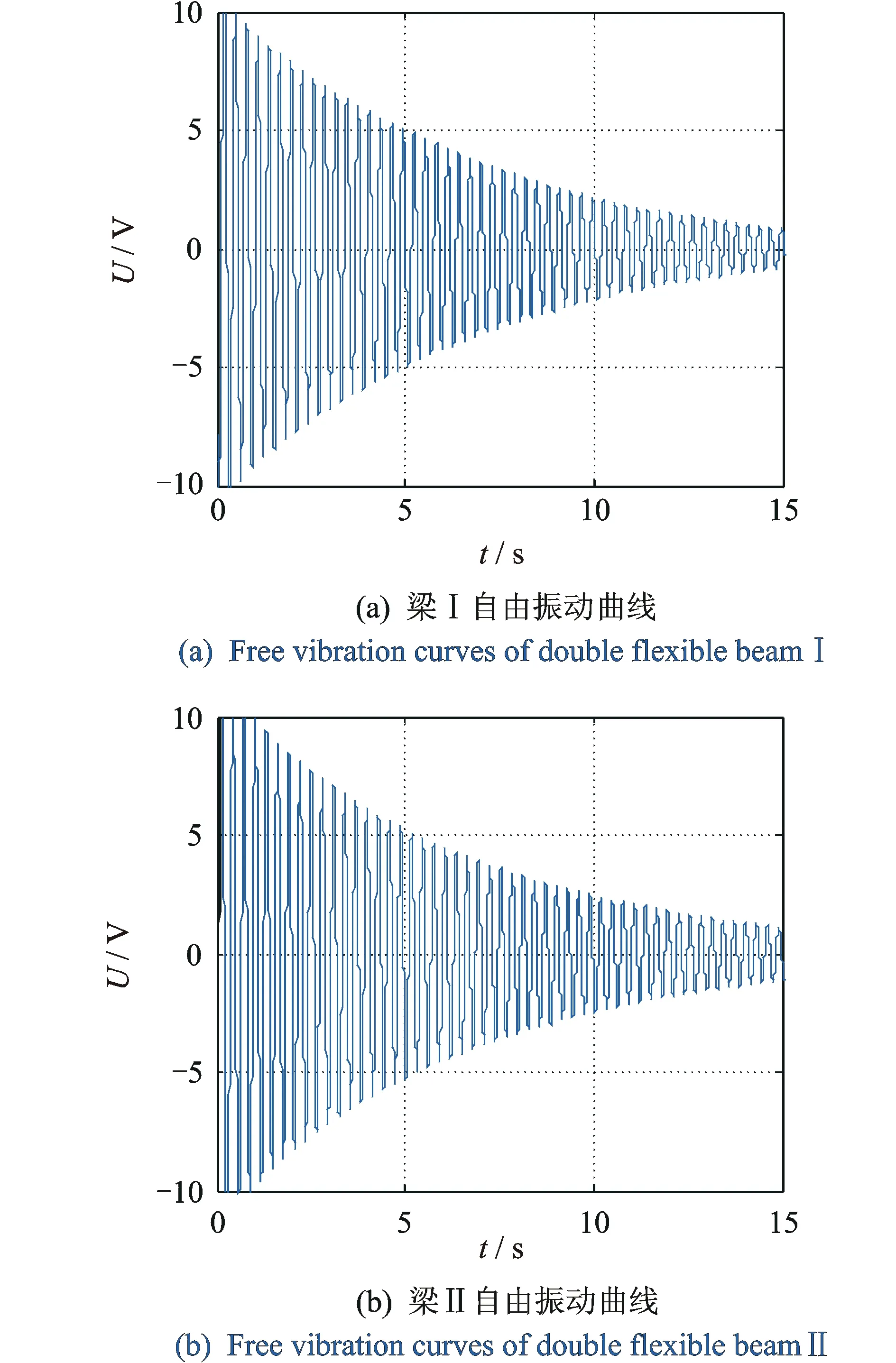
图6 双柔性梁的1阶自由振动曲线Fig.6 Time-domain first mode free vibration curves of double flexible beams

3.2.2 双柔性梁振动控制实验

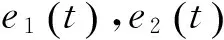
图7显示：在PD算法的控制作用下，梁Ⅰ经过0.5 s衰减至50%，经过5.1 s衰减至10%；梁Ⅱ经过1.4 s衰减至50%，经过3.8 s衰减至10%。在非线性T-S模糊算法的控制作用下，梁Ⅰ经过0.3 s衰减至50%，经过1.8 s衰减至10%；梁Ⅱ经过0.8 s衰减至50%，经过1.6 s衰减至10%。加入伺服电机控制后，算法对双梁大幅值振动的抑制效果有一定的提高，弥补了压电驱动器驱动力小的缺点，但电机对双梁小幅值振动的抑制效果没有明显改进。

梁Ⅰ的振动幅值在整个控制过程中出现了先减小后增加的现象，这主要由于实验采用了伺服电机控制梁Ⅰ的策略，导致梁Ⅱ的振动能量增加，双柔性梁之间存在的强耦合作用促使梁Ⅱ的振动能量传递到梁Ⅰ，梁Ⅰ的振动能量增加。梁Ⅱ的振动在刚加入控制量时趋向于发散，但随着梁Ⅰ的振动被抑制，梁Ⅱ的能量逐渐被梁Ⅰ吸收。实验结果与理论分析得到了一致的结论。同时，借助于压电驱动器的非线性输出特性，小幅值振动在此阶段被快速抑制。相比PD算法，非线性T-S模糊算法对大幅值振动和小幅值振动都具有较好的振动抑制效果。

图7 双柔性梁第1阶振动控制Fig.7 Vibration control of the first mode vibration of double flexible beams

4 结 论

1) 旋转双柔性梁系统具有较大的非线性和耦合性，在行星减速器存在间隙的情况下，双梁的耦合作用体现在双梁以反相振动为主的振动形态。该振动形态使只采用伺服电机控制系统是不可控的。

2) 通过设计多变量非线性T-S模糊控制器，将分段非线性控制和T-S模糊控制结合，实现了非线性、强耦合MIMO系统的定点振动控制。通过压电驱动器和伺服电机复合控制使原有的不可控系统变得稳定。算法较好地解决了减速器存在间隙时双梁的反相振动控制问题。

3) 通过与PD控制算法进行实验对比，所研究的算法具有更好地抑制大幅值振动和平衡点附近小幅值振动的能力。非线性T-S模糊控制算法能在小幅值处保持较大的控制量，从而快速抑制双梁的小幅值振动。同时，控制器加入伺服电机后，双梁的大幅值振动被较快速地抑制。

[1] Liu J, Rong S, Shen F, et al. Dynamics and control of a flexible solar sail[J]. Mathematical Problems in Engineering, 2014,2014:1-15.

[2] Jassim Z A, Ali N N, Mustapha F, et al. A review on the vibration analysis for a damage occurrence of a cantilever beam[J]. Engineering Failure Analysis, 2013,31:442-461.

[3] 曹青松, 洪芸芸, 周继惠, 等. 基于PSO自整定PID控制器的柔性臂振动控制[J]. 振动、 测试与诊断, 2014,34(6)：1045-1049.

Cao Qingsong, Hong Yunyun, Zhou Jihui, et al. Vibration control of flexible manipulator based on self-tuning PID controller by PSO[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(6):1045-1049. (in Chinese)

[4] Chen Longxiang, Sun Jianqiao. Multi-objective optimal design and experimental validation of tracking control of a rotating flexible beam[J]. Journal of Sound and Vibration, 2014,333(19):4415-4426.

[5] 卢全国, 曹清华, 唐刚. 压电复合悬臂梁非线性模型及求解[J]. 振动、测试与诊断, 2014,34(6):1027-1032.

Lu Quanguo, Cao Qinghua, Tang Gang. Nonlinear modeling and numerical solution of piezoelectric cantilever beam[J]. Journal of Vibration, Measurement & Diagnosis,2014,34(6):1027-1032. (in Chinese)

[6] 苏文敬, 吴立成, 孙富春, 等. 空间柔性双臂机器人系统建模、控制与仿真研究[J]. 系统仿真学报, 2003,15(8):1098-1105.

Su Wenjing, Wu Licheng, Sun Fuchun, et al. Dynamics modeling, control and simulation for flexible dual-arm space robot[J]. Journal of System Simulation, 2003,15(8):1098-1105. (in Chinese)

[7] Yu Xiaoyan, Chen Li. Modeling and observer-based augmented adaptive control of flexible-joint free-floating space manipulators[J]. Acta Astronautica, 2015,108:146-155.

[8] 李祖枢, 但远宏, 张小川, 等. 双摆机器人摆杆平衡态任意转换运动控制的实现[J]. 自动化学报, 2010, 36(12):1720-1731.

Li Zushu, Dan Yuanhong, Zhang Xiaochuan, et al. Fulfillment of arbitrary movement transfer control between equilibrium states for a double pendulum robot[J]. Acta Automatica Sinica, 2010,36(12):1720-1731. (in Chinese)

[9] He Shiwen, Jia Qingxuan, Chen Gang, et al. Modeling and dynamic analysis of planetary gear transmission joints with backlash[J]. International Journal of Control and Automation, 2015,8(2):153-162.

[10]Campos J, Lewis F L, Selmic R. Backlash compensation with filtered prediction in discrete time nonlinear systems by dynamic inversion using neural networks[C]∥ Proceedings of the 39th IEEE Conference on Decision and Control． Sydney:IEEE Control System Society,2000:3534-3540.

[11]Wang Zhihong, Wu Yifei, Chen Wei, et al. Discrete second-order sliding mode adaptive controller based on characteristic model for servo systems[J]. Journal of Control Science and Engineering, 2015,ID405376.

[12]Le Tien L, Schaffer A A, Hirzinger G. MIMO state feedback controller for a flexible joint robot with strong joint coupling[C]∥IEEE International Conference on Robotics and Automation. Roma:IEEE Robotics and Automatoin Society,2007:3824-3830.

[13]Heidari S, Piltan F, Shamsodini M, et al. Design new nonlinear controller with parallel fuzzy inference system compensator to control of continuum robot manipulator[J]. International Journal of Control and Automation, 2013,6(4):115-134.

[14]Nagarale R M, Patre B M. Decoupled neural fuzzy sliding mode control of nonlinear systems[C]∥IEEE International Conference on Fuzzy Systems (FUZZ). Hyderabad:IEEE Computation Intelligence Society,2013:1-8.

[15]Sehgal N, Malik M, Chhabra D. Meta-heuristics approaches for the placement of piezoelectric actuators/sensors on a flexible cantilever plate:a review[J]. Meta, 2014,3(6):7-16.

[16]Vörös J. Modeling and identification of systems with backlash[J]. Automatica, 2010,46(2):369-374.

[17]Lin C, Li H. Adaptive dynamic sliding-mode fuzzy CMAC for voice coil motor using asymmetric gaussian membership function[J]. IEEE Transactions on Industrial Electronics, 2014,61(10):5662-5671.

[18]Guerra T M, Vermeiren L. Control laws for Takagi-Sugeno fuzzy models[J]. Fuzzy Sets and Systems, 2001,120(1):95-108.

[19]Huang Jianfeng, Yang Chengying, Ye Jun. Nonlinear pd controllers with gravity compensation for robot manipulators[J]. Cybernetics and Information Technologies, 2014,14(1):141-150.

10.16450/j.cnki.issn.1004-6801.2016.04.024

国家自然科学基金资助项目(51175181)；华南理工大学中央高校基本科研业务费专项资金资助项目(2014ZG0019)

2015-02-05；

2015-04-28

TH113.1； TP273+.4

邱志成，男，1973年10月生，教授、博士生导师。主要研究方向为柔性结构的振动主动控制、机器人控制等。曾发表《基于视觉的柔性结构振动测量及其控制》(《振动、测试与诊断》2012年第32卷第1期)等论文。

E-mail:zhchqiu@scut.edu.cn