IVMD融合奇异值差分谱的滚动轴承早期故障诊断

2016-12-07唐贵基王晓龙

振动、测试与诊断 2016年4期

关键词：变分差分分量

唐贵基, 王晓龙

(华北电力大学能源动力与机械工程学院保定，071003)

IVMD融合奇异值差分谱的滚动轴承早期故障诊断

唐贵基, 王晓龙

(华北电力大学能源动力与机械工程学院保定，071003)

针对滚动轴承早期故障阶段存在特征信号微弱、故障识别相对困难的问题，提出了融合改进变分模态分解和奇异值差分谱的诊断方法。原始信号经改进变分模态分解方法处理后，被分解为若干本征模态函数分量，利用包络谱稀疏度指标筛选出最佳分量构造Hankel矩阵并进行奇异值分解，求取奇异值差分谱后，根据差分谱中的突变点重构信号，最终通过分析信号的包络谱可判断轴承的故障类型。利用改进变分模态分解融合奇异值差分谱的方法对轴承故障模拟及实测信号进行分析，均成功提取出微弱特征信息，能够实现滚动轴承早期故障的有效判别，具有一定的可靠性和应用价值。

改进变分模态分解；奇异值差分谱；滚动轴承；早期故障

引言

实际工程应用中，复杂振动传输路径及严重环境噪声干扰等因素使轴承早期微弱故障特征提取相对困难,这也是故障诊断领域的一个研究热点和难点[1-2]。针对该问题，不少学者进行了研究。文献[3]提出基于小波相关滤波的包络分析方法，成功实现轴承早期故障的判别，但小波基函数的选择缺乏自适应性。文献[4]将循环维纳滤波与包络谱相结合，用于分析轴承全寿命周期故障信号，效果明显，但滤波器处理精度受循环频率估计影响严重。文献[5]提出一种基于双重Q因子的稀疏分解方法，通过分析低共振分量提取微弱特征信息，但该方法参数过多，任一参数设置不合理都会对结果产生较大影响。文献[6]运用最小熵解卷积和包络谱处理轴承早期故障信号，但最小熵解卷积算法的鲁棒性欠佳，容易受信号中少数异常尖脉冲的干扰。文献[7]提出一种自适应信号处理方法——变分模态分解(variational mode decomposition，简称VMD)，该方法在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽，从而能够自适应地实现信号的频域剖分及各分量的有效分离。

笔者对VMD方法进行改进，提出基于能量准则迭代停止条件的改进变分模态分解方法(improved variational mode decomposition，简称IVMD)，并将其引入机械故障诊断领域，用于处理滚动轴承早期故障信号。然而轴承早期故障信号特征信息微弱，噪声干扰严重，如果直接利用IVMD方法对原始信号进行处理，有时效果并不理想。奇异值差分谱[8]能有效描述信号中有用成分和噪声成分奇异值的本质差异，根据差分谱中最大突变点的位置判定有效奇异值的个数，实现信号的降噪及周期成分的提取，将其与IVMD方法相结合，可以提取出更为清晰的故障特征。

1 基本原理介绍

1.1 改进变分模态分解

VMD算法中，本征模态函数(intrinsic mode function，简称IMF)被重新定义为一个调幅-调频信号，其表达式[7]为

(1)

VMD算法在获取IMF分量的过程中摆脱了EMD算法所使用的循环筛分剥离的信号处理方式，而是将信号分解过程转移到变分框架内，通过搜寻约束变分模型最优解来实现信号自适应分解的，每个IMF分量的频率中心及带宽在迭代求解变分模型的过程中不断更新，最终可根据实际信号的频域特性完成信号频带的自适应剖分并得到若干窄带IMF分量。假定将原始信号f分解成K个IMF分量，则对应的约束变分模型表达式为

其中：{uk}={u1,u2,…,uK}为分解得到的K个IMF分量；{ωk}={ω1,ω2,…,ωK}为各分量的频率中心。

为求取约束变分问题的最优解，引入增广Lagrange函数

L({uk},{ωk},λ)=

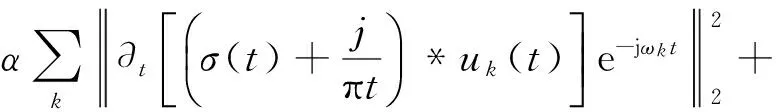
(3)

其中：α为惩罚参数；λ为Lagrange乘子。

利用交替方向乘子算法求取增广Lagrange函数的鞍点，即为式(3)约束变分模型的最优解，从而将原始信号f分解为K个窄带IMF分量。

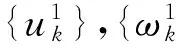
1.2 奇异值差分谱

奇异值分解(singular value decomposition，简称SVD)是一种正交化分解方法，对于任何一个实矩阵A∈Rm×n，都存在一对正交阵U=(u1,u2,…,um)∈Rm×m和V=(v1,v2,…,vn)∈Rn×n，使

A=UEVT

(4)

其中：E=(diag(σ1,σ2,…,σp),0)∈Rm×n或其转置；0为零矩阵；p=min(m,n)；σ1≥σ2≥…≥σp>0为所得的奇异值。

设X=(x(1),x(2),…,x(N))是长度为N的含噪离散数字信号，为了利用SVD方法对其进行降噪处理，须利用该信号构造出Hankel矩阵

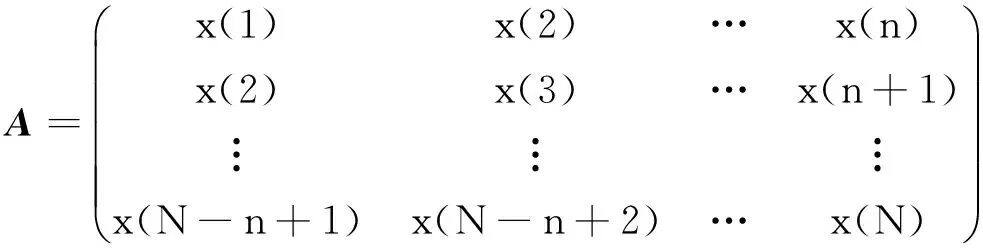
(5)

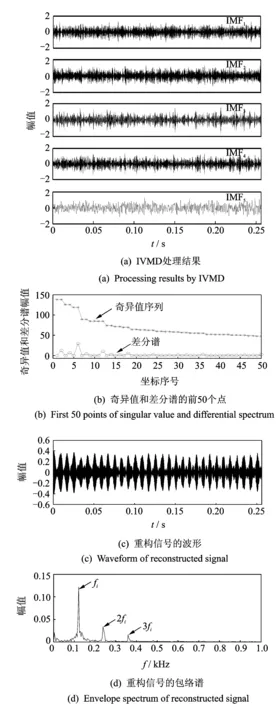
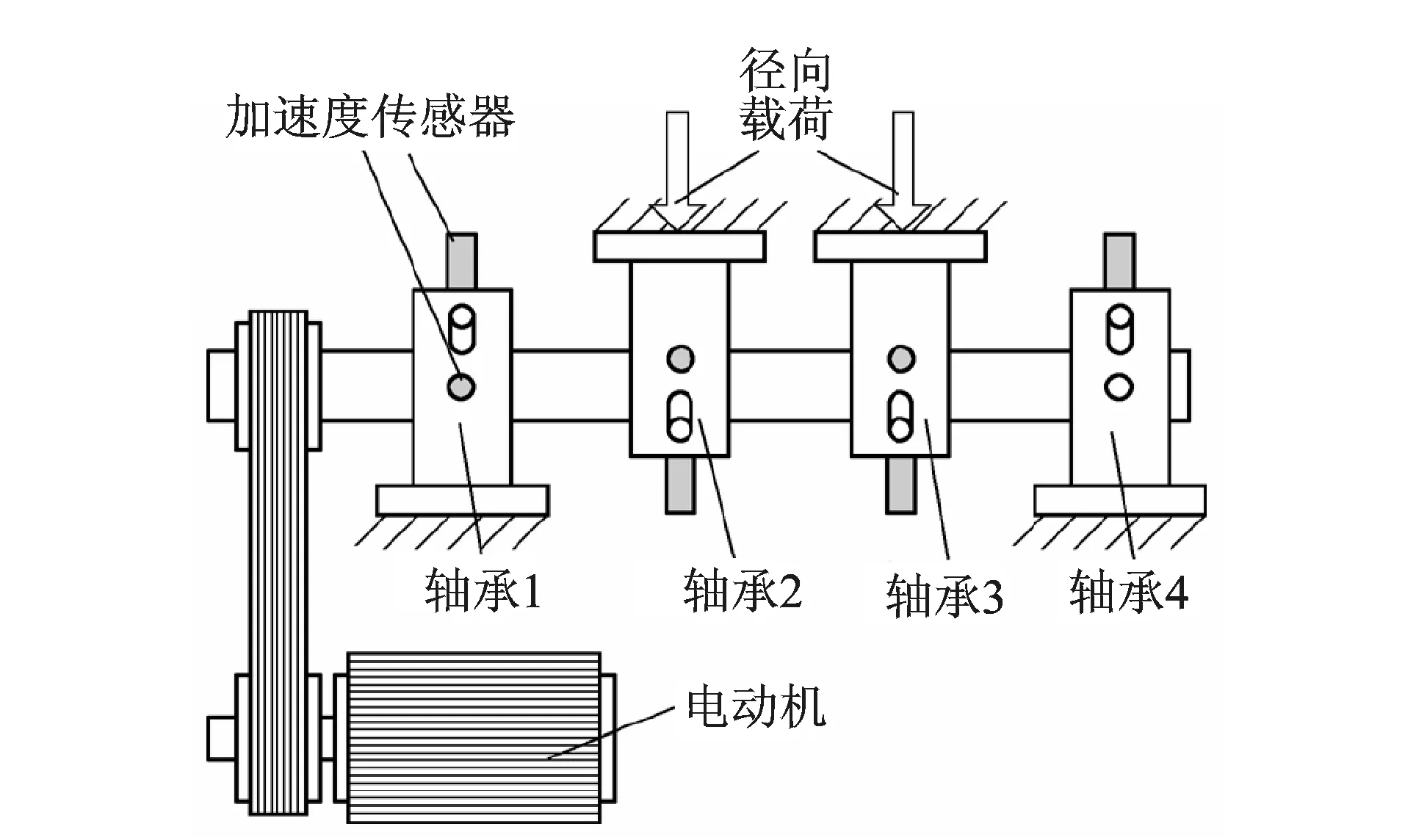
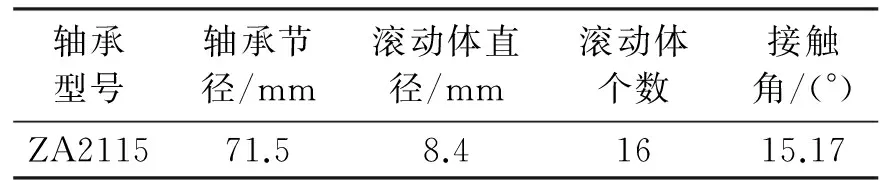
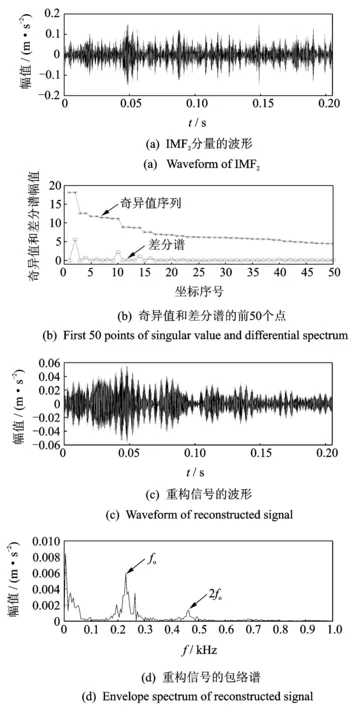
其中:1

由于矩阵的行列数对去噪结果存在直接影响，为实现信号成分的有效分离，需要矩阵的行列数尽可能达到最大，笔者取n=N/2，m=N/2+1。

对Hankel矩阵进行SVD处理，由于有用信号成分对应的奇异值明显大于噪声成分对应的奇异值，因此选取前几个较大奇异值进行信号重构即可达到降噪的目的[9]。为实现有效奇异值个数的自动选取，文献[10]提出了奇异值差分谱的方法，设奇异值按从大到小顺序排成序列E=(σ1,σ2,…,σp)，则

(6)

序列B=(b1,b2,…,bp-1)即为奇异值的差分谱，它描述了相邻奇异值之间的变化情况。最大值bk=max(bi)意味着奇异值序列在该位置处发生了最大突变，因此最大突变点即为信号重构时有用信号成分与噪声成分的分界点。

2 诊断流程

笔者提出了改进变分模态分解融合奇异值差分谱的故障诊断方法，利用IVMD方法对轴承早期故障信号进行处理，原始信号被自适应分解成为若干窄带IMF分量。

稀疏度指标[11]能够有效反应信号的稀疏特性，但是时域信号的稀疏度容易受单个或少量大幅值脉冲的影响。将信号转换到频域，计算信号包络谱的稀疏度则可有效避免这一缺陷。利用IVMD方法处理故障信号后，分别计算各IMF分量的包络谱稀疏度。如果分解分量中包含的噪声较多，与轴承故障相关的周期性冲击特征不明显，则信号包络谱各频率处的幅值相差不大，没有幅值特别突出的成分，包络谱稀疏度相对较小。如果IMF分量中包含的故障特征信息较多，波形中出现规律性连续冲击脉冲，则信号包络谱的相应频率处就会出现较大谱峰，稀疏度也随之增大。鉴于上述分析，笔者以包络谱稀疏度作为指导标准来搜寻最佳IMF分量。图1为改进变分模态分解结合奇异值差分谱的轴承早期故障诊断方法的实现步骤。

图1 具体实现步骤图Fig.1 Graphic of the specific steps

1) 对原始故障信号进行IVMD处理，得到几个频段的窄带IMF分量。

2) 分别计算各IMF分量的包络谱稀疏度，筛选出稀疏度最大的分量作为最佳分量。

3) 利用最佳IMF分量构建Hankel矩阵，并进行SVD处理。

4) 绘制差分谱曲线，确定最大突变点，根据突变点重构信号实现信号降噪的目的。

5) 对降噪信号做包络解调运算，得到包络谱。

6) 将滚动轴承故障频率理论值与包络谱中幅值明显的谱线进行对比，实现故障类型的判别。

3 仿真信号

利用故障模型[12]模拟轴承内圈存在局部缺陷时产生的冲击信号，并添加强烈的白噪声模拟内圈早期故障信号。仿真信号表达式为

其中:s(t)为周期性冲击成分;幅值A0为0.3;转频fr为30 Hz;衰减系数C为700;共振频率fn为4 kHz;内圈故障特征频率fi=1/T=120 Hz;n(t)为高斯白噪声成分;染噪信号的信噪比为-13 dB(信噪比计算公式SNR=20log10(υs/υn);υs和υn分别为冲击成分和噪声成分的有效值);采样频率fs为16 kHz;分析点数为4 096点。

冲击信号波形、内圈早期故障仿真信号波形及频谱如图2所示。对比图2(a),(b)发现，仿真信号中周期脉冲完全被噪声淹没，无规律可循，频谱中4 kHz处的共振频带隐约可见。如图3所示，对仿真信号进行包络谱分析，未发现任何突出频率成分。

图2 仿真信号的波形及频谱Fig.2 Waveform and spectrum of simulated signal

图3 仿真信号的包络谱Fig.3 Envelope spectrum of simulated signal

利用笔者提出的方法对仿真信号进行分析，原始信号经IVMD处理后，自适应地被分解成为图4(a)所示的5个IMF分量。前4个分量的波形中出现较明显的冲击成分，为了从结果中筛选出包含丰富故障特征信息的分量，分别计算各分量的包络谱稀疏度，其中IMF3分量的包络谱稀疏度最大，因此将其确定为最佳分量。利用该分量构造Hankel矩阵进行SVD处理，求取奇异值序列并绘制得到奇异值差分谱。为了观察差分谱的情况，将奇异值序列和差分谱前50个点绘在同一个坐标系下，如图4(b)所示。可以看到，第6个点为差分谱的最大突变点，保留SVD处理得到的前6个奇异值，其余奇异值均置0，进行奇异值重构，得到图4(c)所示的重构信号。SVD的本质是将信号分解成为一系列分量信号的线性叠加，每一个奇异值对应一个分量信号，奇异值越大，对应的分量信号在原信号中的比重越大。由于原信号中添加了较重的噪声干扰，冲击成分的部分特征因强度太小而淹没在噪声中，利用差分谱进行信号降噪时，仅选取前6个较大奇异值对应的分量信号进行重构，使冲击成分的部分特征随着噪声被一起除去，重构信号不会再呈现原本的单边冲击响应特征，但是冲击成分在整个时间段上的周期性并未发生改变。对重构信号做包络解调运算，得到图4(d)所示的包络谱。图中仅fi～3fi处存在3个明显谱峰，谱图干净，无任何干扰成分，故障特征频率及其倍频成分被准确提取出来。

图4 本研究方法的仿真信号分析结果Fig.4 Analysis results of simulated signal by proposed method

为了验证改进变分模态分解方法与奇异值差分谱相结合的必要性，对IMF3分量做包络谱分析，如图5所示。与图4(d)对比发现，图5中虽然内圈故障特征频率fi处谱线幅值比较突出，但是干扰谱线相对较多，且存在一定背景噪声，分析效果与图4(d)相比存在一定差距。

图5 IMF3分量的包络谱Fig.5 Envelope spectrum of IMF3

为突出该方法的优势，利用基于EMD的包络解调方法对仿真信号进行分析。信号经EMD方法处理后，分别求取每个分解分量的包络谱，取效果最好的一个与所述方法的分析结果进行对比。仿真信号经EMD处理后共得到11个分量，如图6(a)所示。计算各分量的包络谱经过对比后发现，仅C1分量的包络谱中出现故障特征频率成分，如图6(b)所示，但特征频率成分十分微弱，很难识别。由此表明基于EMD的包络解调方法无法有效提取出仿真信号中淹没在强烈噪声中的故障特征信息。

图6 基于EMD方法的仿真信号分析结果Fig.6 Analysis results of simulated signal by EMD method

4 全寿命周期加速试验信号

对NSFI/UCR智能维护系统中心的滚动轴承全寿命周期加速试验数据进行分析[13]，试验台转轴上同时安装了4个轴承，转速为2 kr/min，每个轴承的轴向和径向各安装一个加速度传感器，采样频率为20 kHz。图7给出了轴承和传感器的安装位置。

图7 试验平台Fig.7 Experimental platform

试验结束后发现1号轴承外圈出现局部损伤，笔者对该轴承的实测数据进行分析。表1为试验轴承的结构参数，根据结构参数计算得到的外圈理论故障特征频率fo为236.4 Hz。图8为1号轴承振动信号的均方根值趋势。

表1 滚动轴承结构参数

图8 1号轴承振动信号的均方根值趋势Fig.8 RMS trend of vibration signal of No.1 bearing

均方根值变化趋势反映了轴承运行状态的全过程，在7 020 min处，均方根值发生较大跳变，表明状态出现异常，均方根值在9 790min时达到最大，说明轴承已达到寿命极限。图9为7 020 min实测信号的波形及频谱。时域波形出现明显的冲击成分，且冲击间隔比较均匀，频谱在3 000～6 000 Hz范围内，与故障相关的共振频带也很明显，对该组信号进行包络解调运算，得到图10所示的包络谱。谱图主要由外圈故障特征频率及其倍频成分fo～4fo组成，由此很容易识别出轴承外圈故障。

图9 7 020min实测信号的波形及频谱Fig.9 Waveform and spectrum of measured signal in 7 020 minutes

图10 7 020 min实测信号的包络谱Fig.10 Envelope spectrum of measured signal in 7 020 minutes

图11为5 410 min时获取的信号波形及频谱。虽然时域波形中出现少量冲击脉冲，但无法判断脉冲出现的周期。频谱中1 kHz附近存在一个幅值突出的谱峰，属于试验平台的工频干扰。与7 020 min实测信号的频谱相比，该组信号频谱中与故障相关的共振频带并不明显。对其进行包络谱分析，如图12所示，没有出现故障相关频率成分，表明传统的直接包络解调方法对于该组信号无效。

图11 5 410 min实测信号的波形及频谱Fig.11 Waveform and spectrum of measured signal in 5 410 minutes

图12 5 410 min实测信号的包络谱Fig.12 Envelope spectrum of measured signal in 5 410 minutes

利用笔者提出方法对5 410 min实测信号进行分析，信号经IVMD算法处理后，被分解为4个IMF分量，其中IMF2分量的包络谱稀疏度最大，该分量的时域波形如图13(a)所示。观察发现，与原实测信号相比，IMF2分量中冲击成分明显增多，呈现出一定的周期特性，表明原本淹没在强烈背景噪声中的冲击脉冲被有效挖掘出来。利用该分量构建Hankel矩阵后进行SVD处理，得到图13(b)所示的奇异值差分谱,其中第2个点为最大突变点。如果最大突变点发生在前两个点，进行奇异值重构时往往取第2大突变点，因为奇异值个数太少容易丢失有效信息[14]。第2大突变点为第10个点，利用前10个奇异值重构得到图13(c)所示的重构信号。与IMF2分量相比，重构信号中冲击成分的周期特性明显，对重构信号做进一步包络解调运算，得到图13(d)所示包络谱。由于重构信号呈现出低频调制特征，因此包络谱低频段存在一个明显峰值。此外，在外圈故障特征频率fo及其倍频2fo处也出现了幅值突出的谱线，表明轴承外圈已出现局部损伤，理论分析与实际情况相符，且本研究方法与均方根值指标相比提前1 610 min就识别出轴承故障，对于实际诊断应用意义重大。

图13 笔者提出方法的实测信号分析结果Fig.13 Analysis results of measured signal by proposed method

图14 IMF2分量的包络谱Fig.14 Envelope spectrum of IMF2

图14为IMF2分量的直接包络解调分析结果。虽然包络谱中外圈故障特征频率fo处存在一个较明显谱峰，分析效果与原实测信号的直接包络解调结果相比有很大提升，但谱线左侧却存在一个幅值较大的干扰频率成分。对IMF2分量做进一步差分谱降噪后再做包络谱分析，故障特征频率成分变得更加清晰明了，实测信号分析结果也验证了改进变分模态分解与奇异值差分谱相结合的必要性。

利用基于EMD的包络解调方法对实测信号进行处理。信号经EMD处理后共得到10个分解分量，对所得分量依次做包络解调运算，仅在C1分量的包络谱中找到特征频率成分fo，该分量的波形及包络谱如图15所示。由于谱图中特征频率成分不突出且背景噪声干扰严重，因此很容易造成误诊和漏诊，分析效果与本研究方法相比差距较大。

图15 基于EMD方法的实测信号分析结果Fig.15 Analysis results of measured signal by EMD method

5 结论

1) 笔者在介绍变分模态分解方法的同时对其进行改进，提出了基于能量指标停止条件的改进变分模态分解方法。轴承早期故障仿真信号及全寿命周期加速试验信号分析结果表明，将改进变分模态分解与奇异值差分谱相融合能有效提取出信号中隐藏的微弱特征信息，实现轴承早期故障状态的判别。

2) 对比分析结果表明，与传统的直接包络解调方法以及基于EMD的包络解调方法相比，笔者提出的改进变分模态分解融合奇异值差分谱的滚动轴承早期故障诊断方法的分析效果更为有效、准确。

3) VMD作为一种自适应信号处理新方法，笔者首次将其引入到机械故障诊断领域，利用该方法来分析轴承早期故障信号。

[1] 罗颂荣,程军圣,郑近德.基于ITD分形模糊熵的轴承早期故障诊断[J].振动、测试与诊断,2013,33(4)：706-711.

Luo Songrong,Cheng Junsheng,Zheng Jinde. Incipient fault diagnosis based on ITD fractal dimension and fuzzy entropy for bearings[J].Journal of Vibration, Measurement & Diagnosis,2013,33(4)：706-711.(in Chinese)

[2] 杨庆,陈桂明,何庆飞,等.局部切空间排列算法用于轴承早期故障诊断[J].振动、测试与诊断,2012,32(5)：831-835.

Yang Qing,Chen Guiming,He Qingfei, et al. Inchoate fault diagnosis of rolling bearings based on local tangent space alignment algorithm[J].Journal of Vibration, Measurement & Diagnosis,2012,32(5)：831-835.(in Chinese)

[3] 曾庆虎,邱静,刘冠军,等.基于小波相关滤波一包络分析的早期故障特征提取方法[J].仪器仪表学报,2008,29(4)：729-733.

Zeng Qinghu,Qiu Jing,Liu Guanjun, et al.Approach to extraction of incipient fault features based on wavelet correlation filter and envelope analysis[J].Chinese Journal of Scientific Instrument,2008,29(4)：729-733.(in Chinese)

[4] Ming Y,Chen J,Dong G M. Weak fault feature extraction of rolling bearing based on cyclic Wiener filter and envelope spectrum[J].Mechanical System and Signal Processing,2011,25：1773-1785.

[5] 莫代一,崔玲丽,王婧.基于双重 Q因子的稀疏分解法在滚动轴承早期故障诊断中的应用[J].机械工程学报,2013,49(9)：37-41.

Mo Daiyi,Cui Lingli,Wang Jing.Sparse signal decomposition method based on the dual Q-factor and its application to rolling bearing early fault diagnosis [J].Journal of Mechanical Engineering,2013,49(9)：37-41.(in Chinese)

[6] Jiang R L,Chen J,Dong G M,et al.The Weak fault diagnosis and condition monitoring of rolling element bearing using minimum entropy deconvolution and envelop spectrum[J]. Engineering Science Engineers,Part C：Journal of Mechanical Engineering Science，2013,227(5)：1116-1129.

[7] Dragomiretskiy K,Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing,2014,62(3)：531-544.

[8] 胥永刚,孟志鹏,陆明,等.双树复小波和奇异差分谱在滚动轴承故障诊断中的应用[J].振动工程学报,2013,26(6)：965-973.

Xu Yonggang,Meng Zhipeng,Lu Ming,et al. Application of dual-tree complex wavelet transform and singular value difference spectrum in the rolling bearing fault diagnois[J].Journal of Vibration Engineering,2013,26(6)：965-973. (in Chinese)

[9] 张超,陈建军,徐亚兰.基于EMD分解和奇异值差分谱理论的轴承故障诊断方法[J].振动工程学报,2011,24(5)：539-545.

Zhang Chao,Chen Jianjun,Xu Yalan. A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value[J].Journal of Vibration Engineering,2011,24(5)：539-545. (in Chinese)

[10]赵学智,叶邦彦,陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J].机械工程学报,2010,46(1)：100-108.

Zhao Xuezhi,Ye Bangyan,Chen Tongjian.Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe[J].Journal of Mechanical Engineering,2010,46(1)：100-108.(in Chinese)

[11]Tse P,Wang Dong.The design of a new sparsogram for fast bearing fault diagnosis：part 1 of the two related manuscripts that have a joint title as ″two automatic vibration-based fault diagnostic methods using the novel sparsity measurement-parts 1 and 2″[J].Mechanical Systems and Signal Processing,2013,40：499-519.

[12]王宏超,陈进,董广明.基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报,2013,49(1)：88-94.

Wang Hongchao,Chen Jin,Dong Guangming.Fault diagnosis method for rolling bearing′s weak fault based on minimum entropy deconvolution and sparse decomposition [J].Journal of Mechanical Engineering,2013,49(1)：88-94. (in Chinese)

[13]Qiu H,Lee J,Lin J,et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J].Journal of Sound and Vibration,2006,289：1066-1090.

[14]胥永刚,孟志鹏,陆明,等.基于双树复小波和奇异差分谱的齿轮故障诊断研究[J].振动与冲击,2014,33(1)：11-16.

Xu Yonggang,Meng Zhipeng,Lu Ming,et al. Gear fault diagnosis based on dual-tree complex wavelet transform and singular value difference spectrum[J].Journal of Vibration and Shock,2014,33(1)：11-16. (in Chinese)