小学数学“矩形面积图示”的教学价值及教学策略

吴慧容

（仙游县城西中心小学，福建仙游351200）

小学数学“矩形面积图示”的教学价值及教学策略

吴慧容

（仙游县城西中心小学，福建仙游351200）

“矩形面积图示”是指用矩形的长、宽分别表示两个相关联的量，用面积表示这两个量的积的一种几何直观图示，也有人称之为“矩形图”或“面积图”。它的主要教学价值在于能帮助学生辨析概念、理解算理、解决问题和培养创新思维。教学“矩形面积图示”，一要选择合适的教学材料，促进学生逐步形成“矩形面积图示”的认知结构；二要经历描述和分析问题的过程，感受“矩形面积图示”的几何直观作用。

矩形面积图示；教学价值；教学建议

“矩形面积图示”是指用矩形的长、宽分别表示两个相关联的量，用面积表示这两个量的积的一种几何直观图示，也有人称之为“矩形图”或“面积图”［1］。譬如，用矩形的长和宽分别表示单价和数量，用面积表示总价的多少。这种图示的优势在于能够直观地揭示出“因数×因数=积”之类的数量关系。教学中只有把握好它的特点，才能发挥出它的独特价值。

一、“矩形面积图示”的教学价值

（一）辨析概念

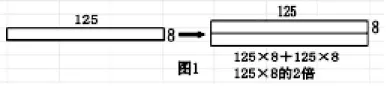
不少小学生往往会背诵却不会应用概念，主要原因在于缺少真正的理解。引入图示构建概念的几何背景，帮助小学生摒弃机械的学习手段，直观地理解概念，不失为概念教学的一种好的方法。“矩形面积图示”作为一种几何直观，在帮助学生辨析某些概念时有着不可替代的作用。“乘法结合律”与“乘法分配律”是学生易混淆的两个概念。例如125×64，通常学生把64分解为8×8，接着就错用乘法分配律：125×(8×8)= 125×8+125×8。纠正这类错误，不能仅仅停留在要求学生观察小括号里是“8×8”而非“8+8”！宜通过建立各自的几何背景帮助学生直观地洞察这两个算式的不同意义。

表征“125×8+125×8”与“125×8×8”的直观图(图 1、图2)：

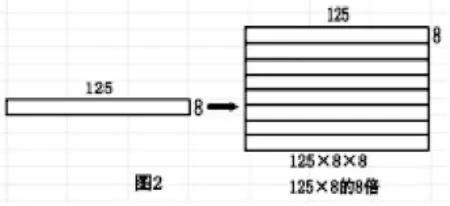
（二）理解算理

“算理直观，算法抽象”是计算教学的不二法门。教学分数乘法，如果说用线段图还好表示的话(图3)，那么用线段图表示就比较困难。相反，用“矩形面积图示”帮助学生理解算理就容易得多(图4)。可见，矩形图在帮助学生理解算理方面具有其独特价值。

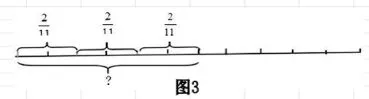
（三）解决问题

小学阶段的某些分数应用题可能会涉及两个相关联而又不相等的未知量，这实质上是一个二元一次方程问题。试举一例：某大型商场上月调进洋品牌空调与国产品牌空调共1200台。现在洋品牌空调已卖出2/5，国产品牌空调已卖出5/8，还有540台没有卖出。问调进的这批空调中洋品牌空调与国产品牌空调各多少台？

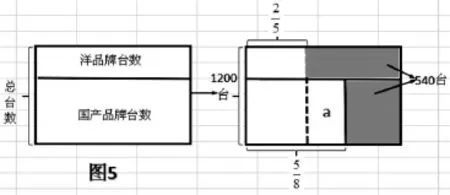
由于题中的两个分数“单位1”不同，用线段图分析其数量关系，必须用两条不等长的线段来表示这两个不相等的量(因为线段图是用线段的长度表示数量大小的)。这势必难以从中找出这两个部分量之间的对应关系，这是线段图的缺陷所在。相比较线段图而言，“矩形面积图示”则容易表征出这类问题的数量关系：构造两个长相同而宽不同的矩形并拼成一个大矩形，两个大小不同小矩形的面积分别代表“两个不同的部分量”。从而容易从中发现两个不相等的部分量之间的对应关系，为分数应用题的化归提供了解题线索。以解决本例谈问题为例，在矩形图中添加如图5中的虚线，标明已知条件，并在“没有卖出的部分”上面涂色或画虚线。如此，解题思路一目了然：

2.720-540=180（台）（利用矩形图的面积关系求出小矩形a表示的空调台数）

4.1200-800=400（台）（洋品牌空调台数）

一旦画成了矩形图(见图5)，相对繁琐的应用题都可以转化成较为简单的求面积问题。可见，“矩形面积图示”还是一个解决数学问题的工具。借助这个工具，能把一些复杂的、抽象的数学问题归结为一类容易解决或已经解决的问题，从而获得解决原问题的答案。

（四）培养创新思维

创新需要可靠的直觉，因为“逻辑用于证明，直觉用于发现”。［2］数学直觉虽然来自主体的潜意识，但是能够在后天自觉的训练中得到培养和提高。“矩形面积图示”作为一种直观背景和几何形象，能够帮助学生在解决某些问题时提供数学思考和直观洞察的机会，具有培养学生数学直觉思维的价值！

以下面的“问题解决”为例：

某班级女生的平均体重是26千克，男生的平均体重是32千克。女生人数是男生的一半。求全班学生的平均体重。小东用男生的平均体重32千克，女生平均体重26千克的和去除以2，得到29千克。他的方法对不对，为什么？

分别有学生用不同方法，证明小东的解法是错的:

第一种：用假设法，假设男生、女生各有若干人，譬如女生10人，那么男生就是20人。然后用常规列式：（32×20+26×10）÷（20+10）=30（千克）；

第二种：考虑极端情况，即如果女生只有1人，那么男生就有2人，这样列式：（32×2+26×1）÷（2+1）=30（千克）；

第三种：通过几何直观，对事物本质有一种直接洞察：①32-26=6（千克）；②26+3+1=30（千克）。

头两种方法容易理解，第三种方法的列式明显具有跳跃性和简约性。该学生先构建矩形图，发现移多补少后有剩余，证明小东的方法是错误的。见图6：

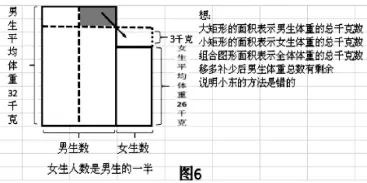
再二次移多补少，跳跃思考简约思维过程，快速地找到正确的答案，见图7：

显然，这个学生在某个程度上具有某种数学上的直觉和想象力，包括几何直观能力，能够根据所面对的问题的本质或特点，提出合情的、富有创见的解决问题的方法与策略。

二、“矩形面积图示”教学策略

与教学其他数学内容一样，“矩形面积图示”应该紧紧围绕“教什么”与“怎么教”这两个方面教学。围绕“教什么”，必须选择合适的内容作为学习材料；围绕“怎么教”，必须选择有利于提高学生几何直观能力的教学方式。

（一）选择合适的教学材料，促进学生逐步形成“矩形面积图示”的认知结构

心理学告诉我们，数学认知结构在学生头脑里是呈板块结构的，呈板块结构状态的数学知识既便于储存，又便于提取。［3］那么，我们应该怎么教学，才能促进学生在头脑里将所掌握的“矩形面积图示”的知识形成系统，组成相应的板块呢？笔者在实践中发现，通过“矩形面积图示”的知识“模块”作为教学材料，引导学生去发现规律、迁移应用往往事半功倍。

例如，解决问题：一块长方形铁板，长17厘米，宽13厘米，如果长裁剪2厘米，宽裁剪3厘米，面积比原来减少了多少平方厘米?

如果有可资利用的学生的错误资源：3×2=6(平方厘米)，那么笔者就会请水平高的学生帮忙：“请你想个办法让他自己发现答案是错误的！”如果没有这样的资源，那么笔者就请会做题的学生上台讲讲：“你们都想想办法，让别人一眼就能看出答案是正确的！”这两种做法，一般都能激发学生自发地画出直观图竭力地去发现或证明(图8)：

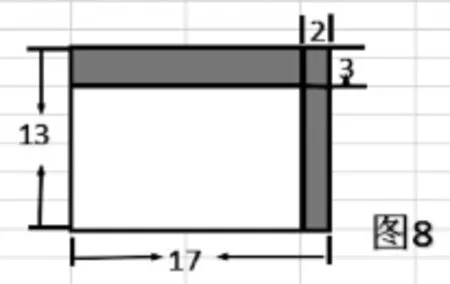
一般地，学生会写出这样的算式：17×13-(17-2) ×(13-3)。这时，笔者会追问：“根据图形的面积关系，你还能想出哪些解决问题的方法？图形的直观性启迪学生再列出下面算式：

1.17×3+(13-3)×2；

2.13×2+(17-2)×3；

3.(17-2)×3+(13-3)×2+3×2.

然后，出示一组变换情境后的“命题链”，并引导学生通过比较、联想，将有关知识简约化、模块化、集成化，进而把数学的“知识结构”内化为个体的数学“认知结构”。

1.下洲村有一个长方形鱼池，长17米，宽13米，因为扩宽道路的需要，鱼池的长要减少2米，宽要减少3米。鱼池的面积比原来减少了多少平方米?

2.乐乐音乐厅原来排列13排椅子，每排17座。因为担心过分拥挤，业主打算不但少放3排椅子，而且每排少放2座。这样总共减少多少个座位？

3.下洲小学原计划到商店购买17副单价13元的乒乓球拍。后来体育组组长发现网购同类球拍每付便宜3元，于是决定改为网购并少买2付。这样一共为学校节省了多少元？

这是应用命题联想系统思想构思的四道数学练习题(含例题)。虽然情境各异，但是几何背景完全相同，所蕴含的数量关系也毫无二致，都可以抽象为：“因数变化后的两积之差”。相信学生采用这样的模块练习，由此及彼、由表及里、由浅及深，融会贯通，对“矩形面积图示”的认识也会深刻不少。

（二）经历描述和分析问题的过程，感受“矩形面积图示”的几何直观作用

“矩形面积图示”是一种几何直观。所谓的几何直观是利用图形描述和分析数学问题，凭借图形对研究对象进行数学思考的一种能力。如果这样的理解大体正确的话，那么“矩形面积图示”的教学重心就应该明确地落在借助“矩形面积图示”表征问题的过程以及表征之后的反思与顿悟上，而不仅仅给予学生一个解题的工具。

举例说明：教学“两位数乘两位数的趣味计算”。这是笔者在教授人教版第六册期末复习“两位数乘两位数”特意增加的内容，目的在于帮助学生进一步打通了形象思维与抽象思维之间的“数学通道”，理解算理，培养学习兴趣。教学过程是这样的：

1.出示问题：一块长方形的菜地长32米，宽23米，这块菜地的面积是多少平方米？题目不难，这是因为把教学重点放在寻找计算的方法上，而不是求面积问题上。

2.当学生列出“32×23=”后，提出要求：“计算前，大家先估一估，这块菜地有多少平方米？”一般地，出现以下三种估算结果：

◆32≈30，30×23=690

◆23≈20，32×20=640

◆32≈30，23≈20，30×20=600

追问：与精确结果相比，你估算的结果是偏大了，还是偏小了？画出长方形图，在图上把估算之内部分与估算之外的部分划分开。

3.精确的计算结果应该包含估算在内的和未估算在内的两个部分。把这两部分合并起来就是题目所要求算出的答案，用竖式怎么算呢？学生用竖式计算后，出示“图9”，再追问：竖式中的“64”表示多少？你能用这个“长方形面积图形”解释每一步的结果吗？通常学生会这样解释:用图中的“③+④”作为第一层的积，用图中的“①+②”作为第二层的积，两层积之和就是“32×23”的积。

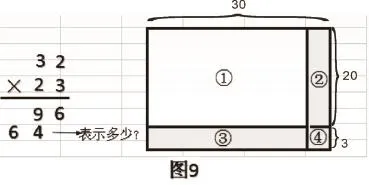
4.继续追问：分别合并图中的“③与④”“①与②”，我们发现了“两位数乘两位数”的竖式通用计算方法。如果换一种合并，那么你们能找到竖式计算的新方法吗？学生分组讨论后交流：“①与④”合并，“②与③”合并，用竖式表示就是图9所示那样。抽象算法“头乘头，尾乘尾，交叉相乘加一加”后，做巩固练习“75× 43=”“56×54=”，熟悉新算法。

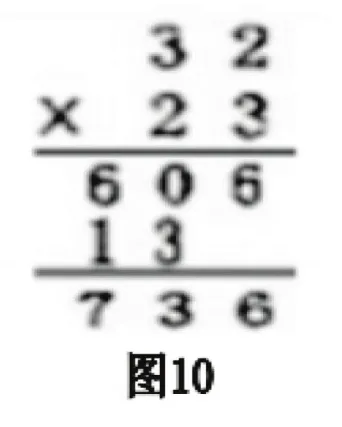
归纳起来，就是先让学生列式、估算求近似值，并主动“划分长方形的面积图”表示估算之内与估算之外的部分，经历用图示表征、解释通用算法的过程。再利用图形特征，让学生反思并实践“换一种图形组合，找竖式计算新方法”。不少学生能顿悟出新的算法这一教学效果证明：只有沟通图形表征、算式表征与计算方法之间的联系，才能获得几何直观的能力。反之，学生可能获得了几何的方法，却未必获得几何直观的能力。

“矩形面积图示”通过作矩形图来展示乘积问题各部分之间的关系来帮助学生理解问题、提高解决数学问题能力，是一种形象的数学模型方法。它在打通形象思维与抽象思维之间的“数学通道”，培养学生几何直观能力方面具有独特的价值和作用。对此，我们应有一个正确的认识，应在适当的时候渗透“矩形面积图示”教学，拓展几何直观的时空，提高学生分析和解决问题的能力。

［1］曹培英.小学数学问题解决的教学研究（四）［J］.小学数学教育，2013（10）.

［2］周林.学家论方法［M］.呼和浩特：内蒙古人民出版社，1985.

［3］光树.数学认知结构［J］.小学数学教育，2001（1/2）.

G633.6

A

1673-9884(2016)06-0062-04

2016-06-04

吴慧容（1968-），女，福建仙游人，仙游县城西中心小学高级教师。