五等跨连续梁模态分析试验及冲击系数
2016-12-06袁向荣蔡卡宏胡帮义
刘 辉, 袁向荣, 蔡卡宏, 胡帮义, 张 盼
(广州大学 土木工程学院,广东 广州 510006)
五等跨连续梁模态分析试验及冲击系数
刘 辉, 袁向荣, 蔡卡宏, 胡帮义, 张 盼
(广州大学 土木工程学院,广东 广州 510006)

分析计算五等跨连续梁的固有频率和振型,探讨连续梁桥冲击系数与其固有频率和振型的关系,并进行了连续梁振动试验,试验模型采用槽型梁,支撑方式采用钢锟轴支撑,试验结果运用DASP模态分析软件进行处理,得到五等跨连续梁的前5阶振型及频率。利用Midas有限元分析软件对连续梁进行有限元分析,将其计算结果与试验结果进行对比,证实振型变化的真实性。经过试验分析,连续梁的前5阶振型最大曲率位置被确定,结合规范讨论计算冲击系数时结构固有频率的选取。结果表明:当计算跨中正弯矩效应时,冲击系数宜按照《桥规》采用基频计算;当计算中支座负弯矩效应时,冲击系数应采用第3阶频率。
五等跨连续梁; 振型; 冲击系数; 有限元分析; 模态分析
0 引 言
连续梁桥是中等跨径桥梁中常用的一种桥梁结构形式,在现代化桥梁设计中,连续梁桥得到了广泛的应用,为了可以较准确的反映桥梁结构在动载作用下的动力增大效应,我们通过冲击系数加以体现。为确保桥梁安全运营,在桥梁结构设计或分析计算时,汽车荷载的总效应应由汽车静载效应乘以冲击系数加以量化考虑[1]。
闫永伦等[2]针对《公路桥涵设计通用规范》(JTJ021-89)中“冲击系数”的规定,提出了制定我国公路桥梁荷载放大谱的建议。《公路桥涵设计通用规范》[3](JTG D60-2004)(以下简称《桥规》)采纳了该建议,采用桥梁基频的函数来计算冲击系数。
《桥规》4.3.2第4款规定,汽车荷载的冲击力标准值为汽车荷载标准值乘以冲击系数μ,第5条规定:当f<1.5 Hz时,μ=0.05;1.5 Hz≤f≤14 Hz时,μ=0.176 7 lnf-0.015 7;f>14 Hz时,μ=0.45,其中,f为结构基频(Hz)。
冲击系数反映了汽车动荷载对桥梁的冲击作用[4],《桥规》中针对连续梁冲击系数的取值由其固有频率所决定。目前关于冲击系数计算的研究主要包括:①根据车辆耦合振动计算探讨冲击系数[5-7];②根据桥梁动载试验实测数据研究冲击系数[8-10];③将我国现行规范与国外规范对照比较,或对我国新旧规范进行比较[2,7,11-12]。
模态分析对于振动工程来说至关重要[13-14],通过分析可以识别结构体系的模态参数,目前连续梁振动的模态分析理论研究较成熟[15-16]。模型与实际试验的频率识别较多,但振型识别较少,而模态叠加法的基础在于振型,振型对于桥梁冲击系数有较大影响[17]。模型试验研究对于多跨连续梁模态分析至关重要,吴晶等[18-20]对二、三、四跨连续梁进行了模态分析计算和试验研究,胡帮义等对二等跨曲线连续梁桥进行了研究,得到了曲梁的前4阶频率及振型;罗川舟等对不同跨径组合的三跨连续梁的振型及频率进行了对比分析;而五跨连续梁还没有试验研究。
总之,《桥规》针对冲击系数的规定是适应的,但连续梁模态分析试验除产生1阶频率外,高阶频率也随之产生,所以研究高阶频率对桥梁结构冲击系数的作用是不可缺少的。姜长宇等的研究表明,对于连续梁桥,冲击系数的计算仅使用基频是不合理的,因此,完整的模态分析对于连续梁桥必不可少。袁向荣[17]基于连续梁振动分析,指出奇数跨连续梁第3阶振型在中支点处曲率较大,故冲击系数应采用第3阶频率计算。
桥梁结构设计的合理性取决于冲击系数的合理取值。本文对五等跨连续梁进行了模态分析试验,得到其前5阶频率及振型,结合试验结果及有限元分析结果,进一步探讨了冲击系数的计算,为今后连续梁冲击系数的计算提供一定的参考。
1 五等跨连续梁试验模型
试验对象为五等跨等截面连续梁模型,梁长5.5 m,桥跨布置为5×1.1 m,共设6个支座,编号为1~6。支承方式为钢辊轴,支座1采用砝码压重约束构成固定支座,其他支座采用直径2.5 cm钢管形成活动支座。连续梁材料采用槽型,横截面如图1所示。

图1 连续梁横截面图(mm)
材料参数取值:弹性模量E=70 GPa,泊松比υ=0.3,线膨胀系数为1.2×10-5/℃,容重Dens=28 kN/m3。试验模型如图2所示。

图2 连续梁试验模型
2 连续梁有限元模态分析
2.1 有限元模型建立
通过Midas Civil 有限元软件建立连续梁有限元计算模型,为使计算结果更加精确,对空间梁单元进行单元划分,将其划分为30个梁单元,并进行各种参数调整。然后进行边界条件处理,对于固定支座1约束其x、y、z方向的位移,其他支座为可动铰支座,只约束z方向位移,模型计算采用集中质量法,将质量转化到z方向。由于加速度传感器的存在,所以在有限元建模时应将每个传感器位置施加一集中力,即G=mg=0.143×9.8=1.40 N,运用将荷载转化为质量的方法施加在模型上,特征值分析设置为子空间迭代,建立的五等跨有限元分模型如图3所示。

图3 有限元分析模型
2.2 有限元计算结果
通过有限元计算分析,得到连续梁前5阶固有频率及振型,频率如表1所示,振型如图4所示。

表1 连续梁各阶频率理论值

(a) 1阶

(b) 2阶

(c) 3阶

(d) 4阶

(e) 5阶
图4 连续梁各阶理论振型图
3 连续梁模态分析试验
3.1 实验仪器及设备连接
本实验所用试验设备有:INV3060V2智能信号采集处理分析仪1台,BI1148型压电加速度传感器10个,联想Y470笔记本电脑1台,DASP V10智能分析软件1套,数据线若干。试验设备连接方式如图5所示。
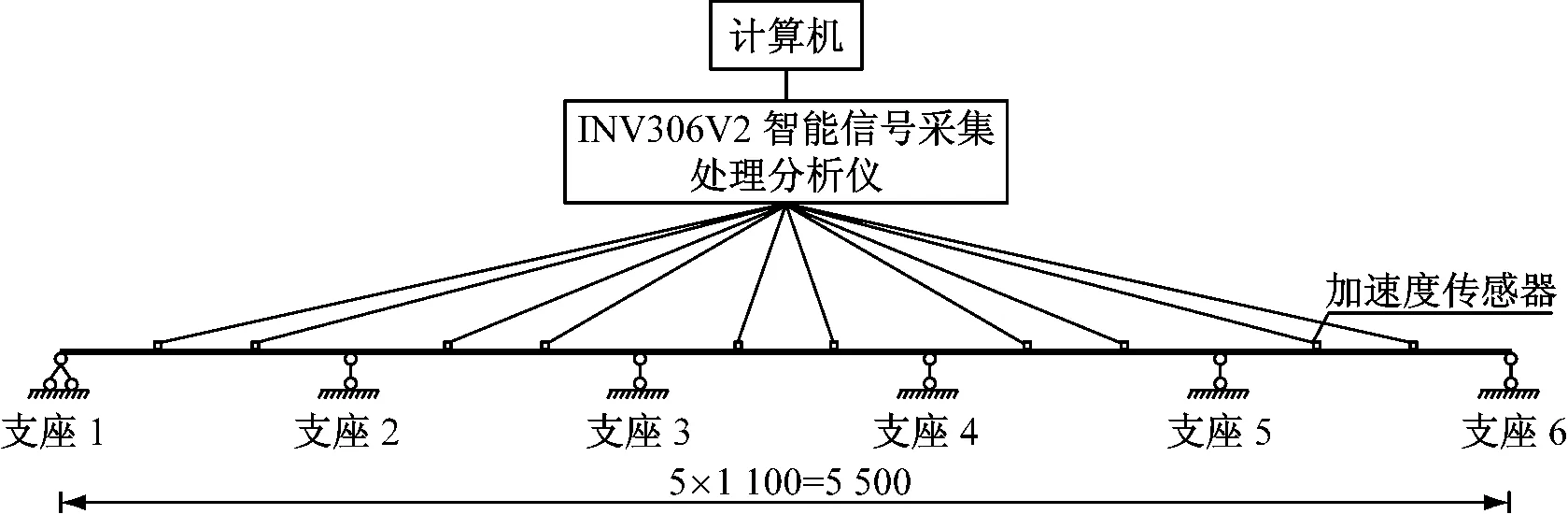
图5 试验设备连接示意图
3.2 试验方法
由于本次试验结构为小型模型试验,所以对试验对象的激励采用锤击法[18]。
3.3 实验过程
首先根据试验要求布置好桥跨和传感器位置,确保各线路畅通及各传感器通道信号显示正常;其次对各通道进行数据标定及各种参数的调整;然后对试验对象进行锤击,采用一点锤击多点测量的办法对实验对象进行激励,同时用信号采集仪采集振动信号并传入笔记本电脑,最后把传入电脑的信号用DASP模态分析程序自动导出传递函数和频响函数,对频响函数进行集总平均,选择恰当的频率定阶。最终进行实模态多自由度拟合,便得到结构的自振频率及其振型图[18]。
3.4 试验结果
通过DASP模态分析软件分析各测点的频响函数曲线得到连续梁的前5阶模态频率及振型幅值。各阶频率如表2所示,振型幅值如表3所示,各阶振型图如图6所示。

表2 各阶频率试验值

表3 各阶实测振型幅值

(a)1阶

(b)2阶

(c)3阶

(d)4阶
(e)5阶
图6 五等跨连续梁前5阶实测振型图
4 结果及对比分析
连续梁试验结果与有限元所得结果列于表4。结果表明:连续连第3阶频率相对误差仅0.2%,第1、2阶相对误差相等为2.1%,第4、5阶相对误差相对较大,但都小于8%;由图4和图6振型图可知,试验测得振型与有限元计算所得振型基本相同;试验所得连续梁前5阶固有频率均小于有限元计算频率。
《桥规》中结构固有频率为冲击系数计算公式的唯一变量,因此,有必要分析固有频率所对应的振型和动弯矩的关系[17]。

表4 有限元结果与试验结果对比
由力学知识可知:梁弯曲时,距中性层距离y的纤维应变为:
(1)
根据几何关系有:

(2)
式中:υ″为中性轴的曲率。联立式(1)、(2)有:

(3)
由式(3)可知,动弯矩M与曲率υ″成正比,即梁的动弯矩随着曲率的增大而增大。按照振动理论[16],振型组成梁振动的完备空间,梁在荷载作用下的动弯矩是其振型的线性组合。对五等跨连续梁1阶振型,各跨最大曲率均在跨中,而其在线性组合中所占比重最大,故最大动弯矩也在跨中。因此计算跨中正弯矩效应时,冲击系数采用基频是合理的。
当考虑支点负弯矩效应时,由图4可知,中支点的曲率最大值在第3、4、5阶振型中均有出现,虽然第4、5阶在中间支座处曲率稍大,但是第3阶振型先出现曲率最大值,故计算中支点负弯矩效应时,冲击系数应采用第3阶频率。
5 结 论
通过有限元计算和试验测试的对比分析,可以得到以下结论:
(1)试验测试分析与有限元分析所得结果除第4、5阶频率相对误差较大外,其他各阶相对误差均小于4%,其频率最大为7.6%,最小为0.1%,试验测得振型与有限元计算振型基本吻合。因此利用模态分析理论对连续梁进行动力特性研究基本是可行的,同时对这两种方法的计算结果进行了相互验证。
(2)对五等跨连续梁桥,其第1阶模态对各跨跨中动弯矩起主要作用,此时跨中处冲击系数最大,因此当计算跨中正弯矩效应时,依据《规范》采用基频计算冲击系数是合理的。考虑支座负弯矩效应时,则不能只按基频计算其冲击系数,应按第3阶频率计算。
(3)对于连续梁桥冲击系数的计算只考虑第1阶频率是不合理的,故在计算连续梁冲击系数时,应根据结构通过有限元计算的频率和振型,参考结构振型最大曲率与正负弯矩选择频率,并用此频率按照相关规范计算冲击系数。
通过试验分析,可以计算连续梁的各阶模态参数,为今后实际桥梁的健康监测提供了参考,也为结构尺寸不详的现有桥梁的结构优化设计和有限元建模提供动力学模态参数参考。
[1] 许 鹏. 桥梁结构冲击系数影响因素研究与试验分析[D].重庆:重庆交通大学,2013:5-13.
[2] 闫永伦,周建廷. 关于我国现行《公路桥涵设计通用规范》“冲击系数”规定的几点探讨[J].公路,2003(6):14-16.
[3] JTG D60-2004.公路桥涵设计通用规范[S].2014.
[4] 王海城,施尚伟. 桥梁冲击系数的影响因素及偏差成因[J].重庆交通大学学报(自然科学版),2007,26(5): 25-28.
[5] 盛国刚,彭 献,李传习. 连续梁桥与车辆耦合振动系统冲击系数的研究[J].桥梁建设,2003(6): 5-7.
[6] 张元文,姜长宇. 公路连续梁桥冲击系数的探讨[J].山西建筑,2008,34(14): 347-348.
[7] 桂水荣,陈水生,任永明. 先简支后连续梁桥车辆冲击系数影响因素研究[J].公路交通科技,2011,28(5): 54-60.
[8] 施尚伟,赵 剑,舒绍云. 梁桥冲击系数实测值与规范取值差异分析[J].世界桥梁,2010(2): 80-82.
[9] 许士强,陈水生,桂水荣. 公路桥梁汽车冲击系数对比研究[J].工程建设与设计,2006(12): 73-75.
[10] 孙伟良. 多跨先简支后连续钢筋混凝土空心板桥梁冲击系数研究[J].石家庄铁道学院学报,2007,20(2): 52-56.
[11] 漆景星. 公路桥梁冲击系数计算方法研究[J].公路,2011(7):85-88.
[12] 刘 舒,王宗林. 关于新旧规范中冲击系数的讨论[J].中国科技信息,2005(23): 121.
[13] 梁 君,赵登峰. 模态分析方法综述[J].现代制造工程,2006(8):139-141.
[14] 龙 英,滕召金,赵福水. 有限元模态分析现状与发展趋势[J].湖南农机,2009,36(4):27-28,45.
[15] 宋一凡.公路桥梁动力学[M].北京:人民交通出版社,2000.
[16] 刘晶波,杜修力.结构动力学[M].北京:机械工业出版,2005.
[17] 袁向荣. 基于连续梁振动分析的桥梁冲击系数研究[J].四川建筑科学研究, 2013,39(4):190-194.
[18] 吴 晶,袁向荣. 两等跨连续梁的模态分析试验[J].长春工程学院学报(自然科学版),2012,13(1):1-2,26.
[19] 郑仰坤,袁向荣. 不同跨径比的两跨连续梁的模态分析试验[J].噪声与振动控制, 2014,34(4):148-152.
[20] 胡帮义,袁向荣,陈泽贤,等. 四等跨连续梁模态试验分析及冲击系数研究[J].实验技术与管理, 2015,32(8):70-74.
Modal Analysis Test to a Five Equal Spans Continuous Beam and Study of Impact Factor
LIUHui,YUANXiang-rong,CAIKa-hong,HUBang-yi,ZHANGPan
(School of Civil Engineering, Guangzhou University, Guangzhou 510006, China)
The natural frequency and vibration mode of 5 equal spans continuous beam was analyzed, the relation between the impact factor of continuous beam and the natural frequencies and vibration mode was discussed, and these dynamic parameters of continuous beam modal were measured. Test model used groove type beam, supporting way was with steel shaft support, the DASP equipment was used for modal analysis to obtain the first five vibration modes and frequencies of 5 equal spans continuous beam. The finite element analysis software Midas was used for continuous beam. The simulation results were compared the measured data, the authenticity of the vibration mode change was verified. From the test analysis, the locations of the maximum curvatures of the mode shapes were determined, the selection of the natural frequency of the beam was discussed with the design code. It is shown that, when calculating the effect of positive bending moment at steady, the fundamental frequency should be used as shown in the general code to calculate the impact factor; when calculating the effect of negative bending moment at middle fulcrum, the 3rd frequency should be used.
five spans continuous beam; vibration mode; impact factor; finite element analysis; modal analysis
2015-07-22
国家自然科学基金(51078093,51278137);广州市科技计划项目(12C42011564)
刘 辉(1991-),男,河南泌阳人,硕士生,研究方向为桥梁工程、数字图像处理。
Tel.:18826223674;E-mail: 18826223674@163.com
U 441.3
A
1006-7167(2016)05-0010-04
