总变差一范数光流场计算综述①

李佳田 李显凯 李应芸 李果家 钱堂慧

(昆明理工大学国土资源工程学院 昆明 650093)



总变差一范数光流场计算综述①

李佳田②李显凯③李应芸 李果家 钱堂慧

(昆明理工大学国土资源工程学院 昆明 650093)

重点回顾与总结了计算光流场的总变差线性一范数方法，简称总变差一范数(TV-L1)方法。通过一致的形式化描述，将亮度守恒模型与梯度守恒模型过渡至全局平滑模型，并着重描述了模型的数值计算过程，透析计算原理与算法底层。最后给出了光流场可视化及质量评估方法，并对总变差一范数方法中的技术难点与下一步工作进行总结。

光流场， 总变差， 数值计算， 算法， 综述

0 引 言

光流场目标的运动速度在图像上的投影[1，2]，其在目标提取、图像重建与图像匹配等方面已有初步应用[3-7]。光流场计算(或光流场估计)实际上是依据图像亮度模式的变化对物体的运动进行估计，因此，解决该问题的一个切入点为：假设运动前后像素点保持亮度一致。然而，亮度一致性假设仅提供了一个约束方程来限定光流的两个分量，不能获取唯一解[8]。为此，Horn和Schunck(HS)、Lucas和Kanade(LK)等分别通过附加全局平滑约束[8]和多点邻域约束[9]的方法以适定光流的解，形成了以HS算法为代表的全局法和LK算法为代表的局部法，其中全局法因能获得稠密光流场、易于集成不同模型进行改进与获取的光流精度高等显著优点而更受青睐。全局法通过数据约束和先验约束下的总误差构成的能量泛函来获取全局最优解，通常将此类方法称为总变差方法。总变差方法的优化技术主要分为三个方面：一是对数据模型进行改进，如利用光学不变测度或多模型结合的方法构建数据约束；二是对平滑模型进行改进，如采用高阶先验约束、加权的先验约束或各向异性的先验约束等；三是总体约束误差的表达，早期的方法采用L2范数来整合单点约束误差，L2范数要求误差满足高斯分布，这在大部分真实场景中不成立。因此，提出了不同的稳健函数来优化误差表达，其中L1范数因效果较好而被广泛使用，此时，认为数据项与平滑项以线性组合方式作用于光流计算，所以称这种方法为总变差线性一范数(total variation linearly1 norm，TV-L1)，简称为总变差一范数，它是目前最主要的光流场计算方法。

通过一致的形式化描述，本文总结了总变差一范数计算方法的基本原理与模型演变，以及透视光流计算中非线性约束下的凸优化问题。在数值计算方法上，通过变分法最小化能量泛函把问题转变为非线性方程组的求解，考虑到计算效率及避免陷入局部最小值，归纳了固定点迭代和金字塔结合的求解策略，使得问题最终简化为大型稀疏线性方程组的求解。

1 基本原理与模型演变

光流场计算产生了多种基本假设模型，这些模型各有优劣，如何选取合适的模型进行集成以获取高精度光流是近年来的研究热点。总变差是不同模型进行集成、优化的强有力工具，形式如下：

EGlobal=EData+αEPrior

(1)

式中EData表示数据项，用于描述原始图像数据随时间的变化不满足特定恒等关系时的误差，由数据约束模型(如亮度守恒模型、梯度守恒模型)给出；EPrior表示先验项，用于描述光流场变化不满足先验恒等关系时的误差，由平滑约束模型给出；α>0，表示正则化参数。

1.1 数据项

1.1.1 亮度守恒假设

亮度守恒假设是光流估计的基本假设，假定目标点发生位移之后像素强度或颜色值保持不变，其隐含了三个假设条件，即目标反射特性(如：假设目标表面为理想散射表面)、场景状态(如：假设场景光照不发生变化)与图像采集传输(如：假设相机成像过程不产生晕影)。如果以f(x, y, t)表示像点(x, y)在t时刻的像素值，以(u(x, y, t), v(x, y, t))表示光流，则亮度守恒假设可表示为

f(x, y, t)=f(x+u, y+v, t+1)

(2)

线性化式(2)，即对其进行一阶泰勒级数展开，则有等式

(3)

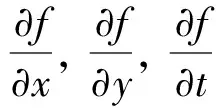
fxu+fyv+ft=0

(4)

1.1.2 惩罚函数选择

式(2)和(4)给出了单点约束误差，关于图像总体误差的表达，Horn和Schunck采用L2范数[8]，则以亮度守恒假设为约束的数据项表示如下：

EData=∑x,y(fxu+fyv+ft)2

(5)

从概率分布的角度来看，采用L2范数意味着假设约束误差满足高斯独立同分布，然而在多数真实场景中，尤其是在边界发生遮挡的区域，此假设并不成立。Black和Anandan[10]使用Lorentzian惩罚函数有效地解决了这一问题。Lorentzian惩罚函数虽然具有很强的稳健性，但因属于非凸函数，使得后续优化过程变得复杂，且容易陷入局部最小值。因此，Brox[11]和Wedel[12]提出采用L1范数克服上述缺陷，并用一个基于Charbonnier函数改写的可微函数来近似L1范数

(6)

式中E是关于单点约束误差Ex, y的向量；‖·‖1表示L1范数；是一个很小的正常数。

1.1.3 光学不变特征

亮度守恒假设是一种理想假设，在自然场景中由于成像设备噪声、光照变化、表面反射以及遮挡等原因往往会使得亮度值发生变化，尤其在某些应用情况下这种变化十分明显，极大违背了亮度守恒假设。早期的算法[13]主要通过对图像进行滤波预处理来消除亮度变化的影响，但改善效果不是很明显，后来有学者提出基于光学不变特征构建数据项，其中梯度特征、纹理特征在算法中被广泛应用。此外，也有学者采用更复杂的特征，如：Liu采用尺度不变特征变换(SIFT)特征[14]、Mileva等采用基于彩色信息的光度不变量[15]。

(1) 梯度特征

图像梯度是指像素值在时间、空间上的导数，由于数字图像是离散化的，每一个像点梯度的求解与周围像点有着密切关系，当发生均匀光照变化时，像点强度值发生变化而梯度值不会改变，为此Brox等[11]提出了梯度守恒假设，即

(7)

(2) 纹理特征

图像可以看作是结构部分和纹理部分的线性组合，光照变化发生后，产生的负面影响主要集中在结构部分，而纹理部分几乎不受影响[12]。因此，以图像纹理特征作为光流计算的输入可避免光照变化的影响。纹理特征的提取通过纹理结构分解(structure texture decomposition，STD)完成，STD基于总变差ROF(rudin osher fatemi)去噪模型实现[16]，对于图像f(x)，其结构部分fs(x)的求解模型为

(8)

其中Ω表示所求图像范围，θ为常数，模型(8)的求解采用原始对偶算法[17]。图像纹理部分fτ(x)为原始图像与结构部分之差，即fτ(α, x)=f(x)-αfs(x)，其中α∈(0,1)，经验证，α取值为0.95时，平均端点误差(Average End-point Error，AEE)最小[12]。

1.1.4 多通道图像

在构建数据项时，如果仅基于单通道图像进行考虑，则数据项无法满足多通道图像的光流场计算，一个较简单的解决办法就是以各通道的总体误差之和来表达数据项：

(9)

1.2 先验项

由于每个像点的光流均包含了两个分量，而式(2)或(4)仅给出一个约束方程来限定这两个分量，即该问题是不适定的，这种现象被称为“孔径问题”[8]。因此，必须增加一个先验项来正则化该病态问题，先验项一般由平滑函数构成。

1.2.1 一阶先验约束

Horn和Schunck根据有限区域内的光流具有相同变化规律的先验知识，提出全局平滑假设[8]，并用光流场的一阶导数来表示，

(10)

约束式(10)主要应用于2帧图像的光流估计，当应用情况变为多帧或整个图像序列的光流场估计时，需要在式(10)中增加时间平滑约束，并使用单向[19]或双向[20]时间校正技术。单向时间校正技术假设光流场随时间是渐变的，即在先验约束中增加时间平滑项∂u/∂t和∂v/∂t。双向时间校正技术需要选择中间帧作为参考进行双向迭代校正，因此，只能在图像帧数已知的情况下使用。

1.2.2 惩罚函数选择

先验项(式(10))采用了L2范数来表示先验约束误差，如1.1.2中所述，真实场景难以满足L2范数的使用条件。Anandan[10]提出在先验项中，通过引进稳健惩罚函数来对该问题进行修正，并在算法中对数据项和先验项运用了一致的惩罚函数。实际使用中，数据项和先验项可不必采取一致的惩罚函数。在多样的惩罚函数中，L1范数的惩罚函数因其显著优点而被广泛使用[11,12]。

在先验项中，惩罚函数有两种作用方式：一是对每一项先验约束误差分别利用惩罚函数，再将其总和作为先验项；二是先求取所有约束误差的平方和或绝对值之和，再对其利用惩罚函数作为先验项。第一种方式有助于获取更加平滑的光流场，Black和Anandan等[10]就采用了这种作用方式；第二种方式因能有效滤除异质点而应用更为广泛，Brox[11]、Wedel[12]与Bruhn[19]均采用了这种方式。

1.2.3 带权先验约束

另一种比较常用的先验约束是带权的一阶约束，即基于图像梯度对L2范数的惩罚函数进行加权：Eprior=∑x, yw(

(11)

其中w是关于像素梯度的权重函数，在边缘处像素梯度较大，对应权重w(f)较小，减弱了对光流的惩罚力度，有利于保留边缘信息。当然，权重函数也可不必基于图像梯度，如Seitz[21]采用分段的权重函数。

1.2.4 各向异性的先验约束

式(11)给出了一个各向同性的先验项，其缺点是无法避免先验约束与数据约束产生的相互干扰问题，应削弱先验约束在数据约束方向的作用力度，增强在数据约束正交方向的作用力度[1]。为此，Nagel[22]和Welberger[20]提出各向异性的平滑模型，使得先验约束在像素梯度方向的作用力度小于像素梯度正交方向；Sun等[23]通过构建可控随机场，根据光流分布及图像结构自适应调整约束方向；Zimmer等[18]提出不再基于像素梯度衡量方向信息，根据数据约束来考虑作用方向。

1.2.5 高阶先验约束

在弱纹理区域，光流估计存在分区域恒定现象[1]，为此Trobin等[24]提出采用二阶先验项来惩罚分区恒定，以欧式向量范数表示如下：

‖·‖=

(12)

高阶的先验约束能产生相对较平滑的光流场，但在边缘处容易产生过度平滑现象，为此，Nir等[21，25]提出采用仿射平滑先验约束获取更精确的光流场。首先参数化光流，然后对于每一像点不再直接求解光流矢量(u(x, y, t), v(x, y, t))，而是求解6个仿射参数，通过所求参数来表示光流：

(13)

(14)

其中(x0, y0)是图像的中点，通过式(13)和(14)可取代数据项直接进行光流求解。

1.3 总变差一范数模型

1.3.1 复合数据项构建

考虑到光照影响及特征提取的简易性，梯度特征是构建数据项的较好选择。然而，由于梯度守恒假设包含了方向信息使得约束式(7)仅在物体发生平移运动时成立[26]，且在后续优化过程中线性化能量函数时图像需满足二次可微条件，在多运动模式并存或一些更复杂的运动模式中，上述限制将会严重降低算法性能[1]。这些缺陷在亮度守恒假设中是完全可以避免的，因此，将基于亮度守恒模型和梯度守恒模型构建复合数据项。

线性化的亮度守恒约束式(4)建立在两个基本假设之上：图像像素强度是连续的；物体的运动是微小的。然而，自然场景中目标的运动难以严格满足这两个条件，因此，在建模阶段依然沿用原始的非线性守恒约束式(2)和式(7)[11]。根据1.1.2中的描述，广义Charbonnier惩罚函数表示如下：

(15)

定义x=(x, y, t)T， w=(u, v, 1)τ，则复合数据项表示为

ED(u, v)=∫Ωψ(|f(x+w)-f(x)|2

(16)

其中γ是两个假设之间的权重，用于调节模型间的相对作用程度。

1.3.2 先验项选择

在1.2中总结了5种不同类型的先验项，从作用方式看，这些模型主要分为两大类：全局平滑模型和有向平滑模型[27]。其中有向平滑模型对噪声比较敏感，且计算较为复杂，应用不如全局平滑模型广泛。基于此，选用一阶先验约束，并采用L1范数的惩罚函数式(15)来保持边缘信息，用光流场的空间梯度算子表示[11]，约束式(10)改写为

EP(u,v)=∫Ωψ(|u|2+|v|2)dx

(17)

式(16)和(17)分别给出了数据项和先验项，根据式(1)可得出总变差一范数光流场计算模型[14]

EG(u, v)=ED+αEP

(18)

现在的目标是需要找到使得式(18)所示泛函EG(u, v)最小的函数u和v，即问题转变为EG(u, v)的最优化问题，通常通过连续优化方法实现。

2 优化方法

在光流场计算中常用的连续优化技术有两种[26]：梯度下降法； 全变分法或极值法。近年也提出了一些比较新的方法，如Trobin[24]和Wedel[12]等采用的解耦算法、Seitz和Baker[21]提出的基于线性规划的凸优算法，但这些方法仍不成熟。梯度下降算法中以最速下降法[26]最为简明，但其需要大量迭代计算才能达到收敛，为此提出了Hessian矩阵的方法[28]，当图像含有N个像素点时，该方法需要求解2N×2N的矩阵及其逆矩阵，因此，梯度下降优化方法仅适用于以LK算法为代表的一类求取未知量较少的算法[9，29]。对于能量函数式(18)的优化，采用全变分法比较合适，根据变分原理，如果式(18)存在最小值，则必满足欧拉—拉格朗日方程[11]：

(19)

另一种与全变分法类似的方法是极值法，以κ表示每个像点的光流(u,v)，极值法通过∂EG/∂κ=0来获取约束方程组，该方法与全变分法的区别仅在于能量函数的逐像素化是在式(19)之前还是之后进行[26]。选用全变分法进行优化，由于EG(u,v)是高度非线性的，最小化过程比较繁琐，因此，为了提高可读性，定义下列缩写表示：

(20)

其中用含z的变量表示特定的差值便于同时间导数进行区分。

用上述变量表示式(19)的结果如下：

(21)

3 模型的数值计算方法

通过变分最小化后，每个像素点将产生如式(21)所示两个非线性方程，假设图像像素点个数为N，则结果为一个含有2N个欧拉-拉格朗日方程式的大型非线性方程组。此时，光流场计算简化为该方程组的求解，通过双重不动点迭代策略[11]消除方程组非线性后可把问题进一步简化为稀疏线性方程组的求解，运用一般的线性方程组解法[26](如雅克比迭代、高斯-赛德尔迭代、超松弛迭代等)即可解出光流。同时，为了避免陷入局部最小值及加快迭代收敛速率，采用不动点迭代和多尺度方法相结合的求解策略[11，30]。

3.1 多尺度运动估计

实现多尺度运动估计主要依靠由粗到细的金字塔结构实现，首先通过下采样建金字塔来构造不同的尺度空间，然后光流估计从粗尺度开始进行，在获取粗略解后，将粗略解映射到精细尺度下做进一步计算。尺度越粗糙，所含像点越少，收敛速度越快，以粗略的解作为精细尺度解的初始值有利于减少迭代次数，提高算法的效率[1]；且粗尺度下的图像含有较少的高频分量，能有效减少局部最小值的数量；在粗尺度下，光流较小，因此对亮度守恒、梯度守恒进行线性化是合理的[26]。

3.1.1 高斯金字塔构建

高斯金字塔构建主要包括高斯滤波和降采样[27]。首先采用高斯滤波作用于原始图像以消除噪声，降低异质点影响，然后通过降采样为金字塔每一层获取数据。

(1) 高斯滤波

高斯滤波是一种线性平滑滤波，被广泛用于图像去噪，其实质是对图像进行加权平均的过程[31]。定义滤波器gfilter，根据正态分布3原则可知位于当前像点3σ个像素外的像点基本不会对当前像点产生影响，则可设置滤波器宽度k=3σ×2+1，得到下式：

(22)

其中i表示滤波器中元素的位置，di表示其对应点距离当前像点的距离，σ通常设置为1。实现高斯滤波的方式一般有两种，一是采用滤波模板与图像做卷积，另一种是通过傅里叶变换实现。σ为1时，模板大小为7×7，卷积运算量较小。由于高斯函数有可分离性，可采用分离滤波器来加快速度，即把二维窗口卷积分离为两次一维卷积运算。

(2) 降采样

降采样过程是建立高斯金字塔的关键步骤，整个过程有两方面需要注意：

① 金字塔采样因子和层数。金字塔采样因子ratio是指当前层与下一层图像行或列的比值，一般采用隔行隔列采样，即ratio=0.5。金字塔层数直接关系着光流计算精度及计算效率，通常由一个给定的最小宽度来控制。

② 下采样插值。下采样插值主要用于构建金字塔过程中不是间隔固定行列采样时非整数坐标取值问题。主要的插值方法有双线性插值[7]和双三次插值[32]，后者获得的图像具有更好的平滑性。

3.1.2 光流逐层估计

逐层估计包含了金字塔不同层级间的增量校正过程及同一层级间的光流迭代更新过程，其计算过程将在3.2节给出，本节着重关注逐层估计中的Warping处理。Warping处理是指通过已解出的光流在第2帧上封装出一幅新图像[11]，其主要作用于两个过程：一是在低分辨率层光流场向高分辨率层映射；二是内层迭代(详见3.3节)结束后通过Warping处理缩小与第1帧图像的残差。其中，对于非整数坐标取值问题采用双线性或双三次插值解决，光流(u，v)越界问题通过下式处理：

(23)

3.2 外层不动点迭代

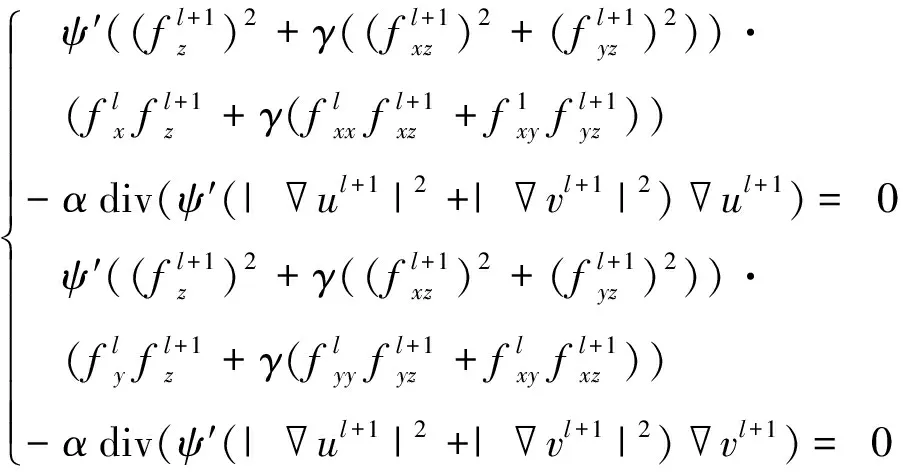
(24)

然后把未知量ul+1，vl+1分离为前一步的迭代结果ul，vl和未知增量dul，dvl。设

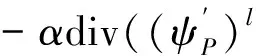
(25)

3.3 内层不动点迭代

(26)

3.4 梯度、散度离散近似

采用有限差分近似像素梯度与光流梯度。设定当前点位置(x, y)，对于宽M、高N的图像，光流增量du水平方向梯度的前向差分如下：

(27)

竖直方向梯度，

(28)

梯度的散度采用后向差分结果表达，目的是通过在前向差分结果上进行后向差分等价实现二阶中心差分：

(29)

式(26)经过差分近似后可得到两个线性方程式，则图像上所有像点对应的方程式就构成了一个大型的线性方程组。其中，待求解的列向量即为光流场增量，为加快收敛速度，采用超松弛迭代法[33]求解。

总变差一范数光流算法流程图如图1所示。

4 光流场可视化与质量评价

4.1 可视化

通过总变差一范数算法，可以获得一个致密的光流场，如何在图像上以直观的方式对光流场进行显示也是一个重要的问题。目前光流场显示主要有三种方法：灰度图、二维矢量图与彩色蕴含图[26]。

(1) 灰度图。对于流场的两个分量场，由于其值有正有负，因此将光流绝对值化后再进行归一化处理，就可以用两个灰度图来进行显示，但是这种显示方案在绝对值化时舍去了流场的方向信息，因此只能用于运动物体检测，无法提供更多运动相关信息。

(2) 二维矢量图。二维矢量图是比较直观显示方案，主要通过有向线段来表示光流矢量。由于每个像点具有一个光流矢量，为了观察方便，通常采用稀疏流场或放大的流场显示。

图1 总变差一范数光流算法流程图

(3) 彩色蕴含图。由于人眼对彩色的分辨能力比对灰度的强，因此基于彩色信息来表达光流有利于肉眼观察。彩色蕴含图是一种比较常用的显示方法，它一般基于面向视觉感知的颜色模型(如HIS、HSV等)来进行显示。其中，最常用的是HIS模型，它采用三个参数—色调、饱和度、亮度来描述颜色。当饱和度、亮度固定时，把最敏感的红、绿、蓝三种色调间的连续变化用离散圆域来表示，构成孟塞尔色轮。由于光流场是一个二维向量场，因此，可以将光流值与色轮上的颜色值一一对应，按相应颜色值进行显示即可得到一个彩色表示的光流场。

4.2 质量评价

(30)

AAE定义为

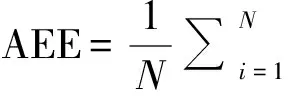
(31)

5 总结与展望

光流场算法一直致力于对孔径问题、成像噪声、运动不连续性、无纹理区域、光照变化、大位移光流、非刚体运动、小目标等方面进行改善，并取得了显著成果，但要在实际中深入应用，还需着重解决以下几个方面的问题：

(1) 设计合适的优化算法。目前广泛使用的优化方法都属于连续优化算法，此类算法通过数值迭代获取光流解，但每次迭代只能实现微小的更新，使得算法效率不高。许多学者提出了离散优化算法(如图割法[35]、置信度传播[36]等)。离散优化算法是在一个事先定义的离散的光流空间里搜索最优解，有利于可提高收敛速度，但此类方法尚属于起步阶段，存在着许多问题需要解决[1]。

(2) 复杂光照变化的影响。由于受阴影遮挡、拍摄角度与成像传输设备的影响，光流算法对亮度变化异常敏感，无法进行精确光流估计。为此，对图像进行滤波预处理、寻求光学不变特征、多模型结合等方法被用来改善算法在光照变化下的估计效果，此举在一定程度上降低了光照变化带来的不利影响，但由于真实场景中光照变化的复杂性，目前还没有一种算法能够自适应地解决复杂光照变化问题[1]，该问题严重限制着光流技术在实际中的应用。

(3) 大位移运动估计。虽然采用了由粗到细的金字塔法来解决大位移光流的获取，但是所能估计的位移尺度依然有限，Alvarez等[37]通过对基本光流场进行多方面改进后能解决10个像素大小的位移估计问题，但如何获取更大位移的光流依然是值得考虑的问题。由于传统的金字塔法提供的改进空间有限，可考虑融合其他图像特征作为引导信息来降低最优化的搜索范围及难度[38]。其次是小目标的大位移问题，为实现多尺度的方法，需要构造许多不同的尺度空间，这样将会造成低分辨率下小目标的丢失而无法估计其光流，融合通道表示下描述符匹配的方法[39]可以实现对小目标的捕捉，但是该方法不能有效处理结构复杂的运动图像，因此如何更好地对小目标的运动进行估计依然值得深入研究。

(4) 算法实时性。当光流技术应用到机器人导航、视频运动目标跟踪这些场景下时，必须考虑算法实时计算性能。为了求解非线性系统及获取大位移光流，需要采用不动点迭代、多尺度运动估计等求解策略，这就会极大地增大算法的时间复杂度，且整个估计过程需要逐层、逐点进行迭代计算，随着图像增大，大量浮点运算将会给CPU带来沉重负荷，因而设计结合GPU的并行处理架构或采用多核处理器将会为实时系统的构建提供有力支持[1，38]。

[1] 宋爽, 杨健, 王涌天. 全局光流场估计技术及展望. 计算机辅助设计与图形学学报, 2014, 26(5): 841-850

[2] 涂志刚, 谢伟, 熊淑芬等. 一种高精度的TV-L1光流算法. 武汉大学学报·信息科学版, 2012, 37(4): 496-499

[3] 范冲, 龚健雅, 朱建军等. ALOS-PRISM遥感影像超分辨率重建. 遥感学报, 2009, 13(1): 75-82

[4] 陈王丽, 孙涛, 陈喆等. 利用光流配准进行嫦娥一号CCD多视影像超分辨率重建. 武汉大学学报·信息科学版, 2014, 39(9): 1103-1108

[5] 闫利, 巩翼龙, 张毅等. 光流动态纹理在土地利用/覆盖变化检测研究中的应用. 光谱学与光谱分析, 2014, 34(11): 3056-3061

[6] 张正鹏, 江万寿, 张靖. 光流特征聚类的车载全景序列影像匹配方法. 测绘学报, 2014,43(12): 1266-1273

[7] 王昊京, 王建立, 王鸣浩等. 采用双线性插值收缩的图像修复方法. 光学精密工程, 2010, 18(5): 1234-1241

[8] Horn B K P, Schunck B G. Determining optical flow.ArtificialIntelligence, 1981, 17(1):185-203

[9] Lucas B D, Kanade T. An iterative image registration technique with an application to stereo vision. In: Proceedings of the 7th International Joint Conference on Artificial Intelligence, San Francisco, USA, 1981, 81: 674-679

[10] Black M J, Anandan P. The Robust Estimation of Multiple Motions: Parametric and Piecewise-Smooth Flow Fields.ComputerVisionandImageUnderstanding, 1996, 63(1): 75-104

[11] Brox T, Bruhn A, Papenberg N, et al. High accuracy optical flow estimation based on a theory for warping. In: Proceedings of the 8th European Conference on Computer Vision, Heidelberg: Springer, 2004, 3024: 25-36

[12] Wedel A, Pock T, Zach C, et al. An improved algorithm for TV-L1 optical flow. In: Lecture Notes in Computer Science. Heidelberg: Springer, 2008, 5064: 23-45

[13] Anandan P. A computational framework and an algorithm for the measurement of visual motion.InternationalJournalofComputerVision, 1989, 2(3): 283-310

[14] Liu C, Yune J, Torralba A, et al. SIFT flow: dense correspondence across difference scenes. In： Proceedings of the 10th European Conference on Computer Vision, 2008, 5304:28-42

[15] Mileva Y, Bruhn A, Weickert J. Illumination robust variational optical flow with photometric invariants. In: Proceedings of the DAGM Symposium on Pattern Recognition. Heidelberg: Springer-Verlag, 2007. 152-159

[16] Rudin Li, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms.PhysicaD, 1992, 60(1-4): 259-268

[17] 李秀智, 谭君, 贾松敏等. 基于结构纹理分解和多重网格的光流估计算法. 上海交通大学学报, 2014, 48(7): 959-964, 970

[18] Zimmer H, Bruhn A, Weickert J, et al. Complementary optic flow. In: Proceedings of the 7th international workshop on energy minimization methods in computer vision and pattern recognition, Bonn, Germany, 2009, 5681: 207-220

[19] Bruhn A, Weickert J, Schnorr C. Combine local and global optical flow methods.InternationalJournalofComputerVision, 2005, 61(3): 211-231

[20] Werlberger M, Trobin W, Pock T, et al. Anisotropic Huber-L1 optical flow. In: Proceedings of the British machine vision conference, Manchester, UK, 2009. 1-11

[21] Seitz S M, Baker S. Filter flow. In: Proceedings of the 12th IEEE International Conference on Computer Vision. Los Alamitos, USA, 2009. 143-150

[22] Nagel H, Enkelmann W. An investigation of smoothness constraints for the estimation of displacement vector fields from image sequences.IEEETransactionsonPatternAnalysisandMachineIntelligence, 1986, 8(5): 565-593

[23] Sun D, Roth S, Lewis J, et al. Learning optical flow. In: Proceedings of the 10th European conference on computer vision, Heidelberg: Springer, 2008, 5304: 83-97

[24] Trobin W, Pock T, Cremers D, et al. An unbiased second-order prior for high-accuracy motion estimation. In: Proceedings of the 30th DAGM Symposium Munich, Heidelberg: Springer, 2008, 5096: 396-405

[25] Nir T, Bruckstein A M, Kimmel R. Over-parameterized variational optical flow.InternationalJournalofComputerVision, 2008, 76(2): 205-216

[26] Baker S, Scharstein D, Lewis J P, et al. A Database and Evaluation Methodology for Optical Flow.InternationalJournalofComputervision, 2011, 92(1): 1-31

[27] 项学智, 开湘龙, 张磊等. 一种变分偏微分多模型光流求解方法. 仪器仪表学报, 2014, 35(1): 109-116

[28] Baker S, Matthews I. Lucas-Kanade 20 years on: a unifying framework.InternationalJournalofComputerVision, 2004, 56(4): 221-255

[29] Le Besnerais G, Champagnat F. Dense optical flow by iterative local window registration. In: Proceedings of the International Conference on Image Processing, 2005, 1:137-140

[30] Lei C, Yang Y H. Optical flow estimation on coarse-to-fine region-trees using discrete optimization. In: Proceedings of the 12th IEEE International Conference on Computer Vision. Los Alamitos: IEEE Computer Society Press, 2009, 1562-1569

[31] 李秀智, 尹晓琳, 贾松敏等. 改进的TV-L1平滑光流估计. 光学学报, 2013, 33(10): 188-194

[32] 庞志勇, 谭洪舟, 陈弟虎. 一种改进的低成本自适应双三次插值算法及VLSI实现. 自动化学报, 2013, 39(4): 407-417

[33] 李庆扬, 王能超, 易大义. 数值分析. 北京：清华大学出版社, 2006

[34] Baker S, Scharstein D, Lewis J P, et al. The middlebury computer vision pages [BE/OL]. http://vision.middlebury.edu/flow/

[35] 路子赟, 唐土生, 高隽等. 带有局部控制因子的图割光流估计. 中国图像图形学报, 2012, 17(7): 846-852

[36] 郁理, 郭立, 袁红星. 基于分级置信度传播的立体匹配新方法. 中国图像图形学报, 2011, 16(1): 103-109

[37] Alvarez L, Weickert J, Sanchez J. Reliable estimation of dense optical flow field with large displacements.InternationalJournalofComputerVision, 2000, 39(1): 41-56

[38] 李秀智, 贾松敏, 尹晓琳等. 视觉光流矢量场估计算法综述. 北京工业大学学报, 2013, 39(11): 1638-1643

[39] Laura S, Deqing S, Erik G, et al. Optical flow estimation with channel constancy. In: Proceedings of the 13th European Conference, Switzerland: Springer, 2014, 8689: 423-438

A review on TV-L1optical flow field calculation

Li Jiatian, Li Xiankai, Li Yingyun, Li Guojia, Qian Tanghui

(Faculty of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093)

The method for optical flow field calculation using the Total Variation Linearly 1 norm, called the TV-L1method for short, is reviewed and summarized emphatically. By means of the coherent formal description, the bright conservation model and the gradient conservation model are transferred to a global smooth model, and the models’ numerical computing progress, analytical calculation principle and physical level of algorithm are emphatically described. At the end, the method for visualization of optical flow fields and the method for quality assessment optical flow fields are given, and the technical difficulties of the TV-L1and its future work are concluded.

optical flow field, total variation, numerical calculation, algorithm, review

10.3772/j.issn.1002-0470.2016.04.004

①国家自然科学基金(41561082， 41161061)资助项目。

，E-mail: 1132468376@qq.com(

2016-01-26)

②男，1975年生，博士，硕士生导师，副教授；研究方向：视觉测量与机器场景理解；E-mail： ljtwcx@163.com