单导联脑电信号P300少试次提取算法研究①

胡春海 信思旭 刘永红

(燕山大学河北省测试计量技术及仪器重点实验室 秦皇岛 066004)



单导联脑电信号P300少试次提取算法研究①

胡春海②信思旭 刘永红

(燕山大学河北省测试计量技术及仪器重点实验室 秦皇岛 066004)

研究了脑电(EEG)信号中的正向电位P300的提取，为了克服P300信号提取中对电极数量和试验次数的苛刻要求，提出了一种单导联脑电信号P300少试次提取新方法，该方法首先对原始信号进行小波变换去噪处理，利用分离盲源的特征矩阵联合近似对角化(JADE)算法对得到的观测信号进行分解；其次为避免少试次提取中可能存在的突发性错误，依据皮尔逊相关系数(PCC)和列向标准差构建层次分析模型，对P300分量进行最优提取；最后利用时域能量熵的统计分布特性和小波变换原理对重构后的P300信号进行时频域的补偿。试验结果表明，该方法只需对单导联3试次的数据进行处理，并能够有效地提取P300成分。

脑电信号处理， P300， 时域能量熵， 小波变换， 层次分析模型

0 引 言

脑-机接口(brain computer interface, BCI)是在人脑和计算机或其他电子设备之间建立的不依赖于常规大脑信息输出通路的对外信息交流和控制的通信系统。作为事件相关电位(event related potential, ERP)中重要的内源性成分，P300脑电信号(EEG倍号)被广泛应用于BCI系统中[1-3]。P300是受试者受到发生概率较小的外界事件刺激时在头顶中缝区域内诱发的潜伏期为300ms左右的正向电位，不需要初始训练，刺激物与被试者的利害关系及被试者的情绪都会在P300上有所反映。然而P300成分十分微弱，实际采集到的EEG信号伴随着大量的神经源性噪声和非神经源性干扰，因此如何从EEG数据中提取出P300成分对认知生物科学和电子与信息科学等研究具有十分重要的意义[4]。

目前针对P300特征提取技术有很多方法，包括相干平均、参数模型、自适应滤波、小波分析[5]、神经网络[6]以及主成分分析[7, 8]等，均能够较好的提取P300成分，并达到可观的分类效果，但是其大量的导联数目增加了BCI系统操作的繁琐程度，冗杂的EEG数据也会严重加大算法的计算负荷，任一导联数据采集的好坏均会对BCI系统的识别结果产生影响；另外，由于EEG信号低信噪比和非平稳随机的特点，即使对于同一被试，诱发的P300也可能存在一定的区别，多次平均忽略了试验之间的差异性，多次刺激容易引起被试者的神经性疲劳，从而影响波形，这些均很难满足BCI系统在线应用的要求。针对上述问题，本文提出一种单导联脑电信号P300少试次提取的新方法，将小波变换与盲源分离(blind source separation, BSS)相结合，利用层次分析模型提取源信号估计分量中的P300成分，并结合时域能量熵的统计分布特征对重构后的信号进行时域和频域的补偿。

1 试验描述及数据来源

试验所用数据来自于BCI Competition II中的Data set IIb，该数据由基于经典Oddball范式的拼写器试验产生，使用标准化的64导联电极帽采集，并通过BCI2000系统记录，记录部位按照国际10-20导联系统分布。试验中，被试者面对一个6×6字符矩阵，并集中注意力观察要拼写的字符。对于每一个待选的字符，矩阵的行和列都会随机高亮12次，其中必定有一行和一列的高亮包含了所需要的字符，这样即构成了概率分别为0.17和0.83的偏差刺激和标准刺激。被试者对偏差刺激所在行和列的高亮次数进行计数，便构成了具有随机性和突发性的靶刺激，该刺激诱发的脑电信号中便含有强度较大的P300成分。

P300的头皮分布相对集中在中线部位，其波幅在顶后部Pz处和中央顶部Cz处较大。大量试验表明中央顶部记录的信号效果更为明显，因此只选择电极Cz处的EEG数据进行分析处理。对单导联采集到的数据分段整理，试验共拼写42个字符，每个字符进行15次试验，共得到1260次靶刺激和6300次非靶刺激数据段，每个数据段以刺激时刻0开始，到1000ms结束，因采样频率是240Hz，则每一次刺激的数据长度为240。

2 单导联脑电信号P300少试次提取算法

提取单导联3试次脑电信号中P300成分的过程如图1所示。具体提取步骤如下：

步骤1：对3试次的原始信号分别进行小波变换处理，滤掉0～7.5Hz之外的噪声干扰。

步骤2：利用盲源分离的特征矩阵联合近似对角化(joint approximate diagonalization of eigenmatrices, JADE)算法对观测信号进行分解，得到3个源信号的估计分量。

步骤3：依据相关系数和列项标准差构建层次分析模型，对P300分量进行最优提取，并结合混合矩阵重构P300信号。

步骤4：依据时域能量熵的统计分布特性对重构后的P300信号进行熵值调整，并利用小波变换作平滑处理，进行时频域的信号补偿。

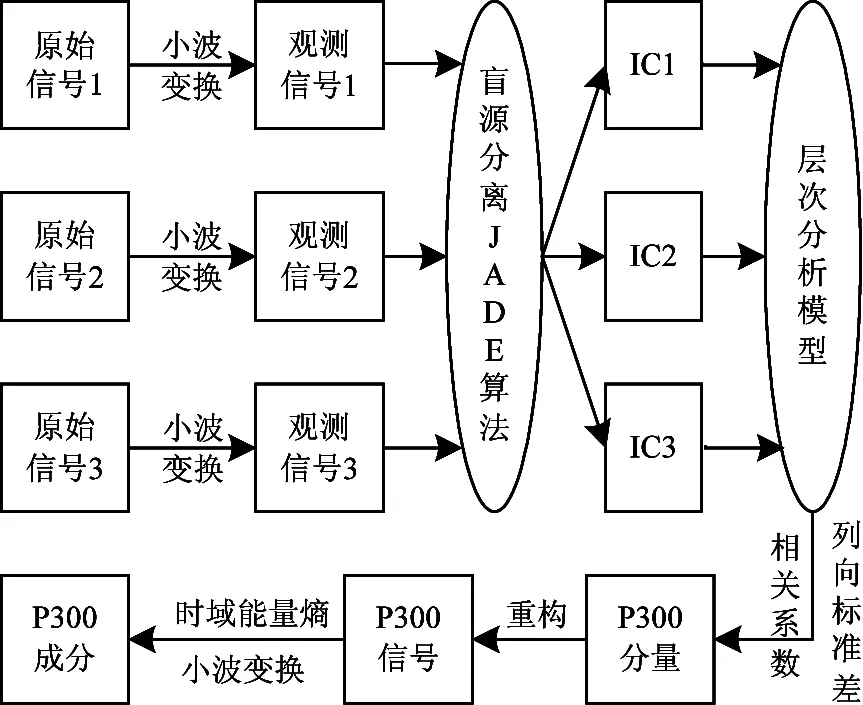
图1 单导联脑电信号P300少试次提取算法流程

2.1 基于小波变换的频域滤波

P300的频谱主要集中分布在低频区域，尤其是2～8Hz之间的EEG信号对P300的提取结果影响较大，为了滤除其频率之外的噪声干扰，选取小波变换[9]作为P300脑电信号的频域滤波方法。具体步骤为：

(1) 母小波采用Daubechies4小波，对每个EEG信号进行4层小波分解。

(2) 将分解得到的不同尺度下的高频细节分量置零处理。

(3) 进行多层小波重构，得到频带为0～7.5Hz的小波去噪后的脑电信号。

如图2、图3所示，随机选取3组电极Cz处的靶刺激信号作为原始EEG信号，对其进行上述小波变换处理，得到频域滤波后的3组观测信号。

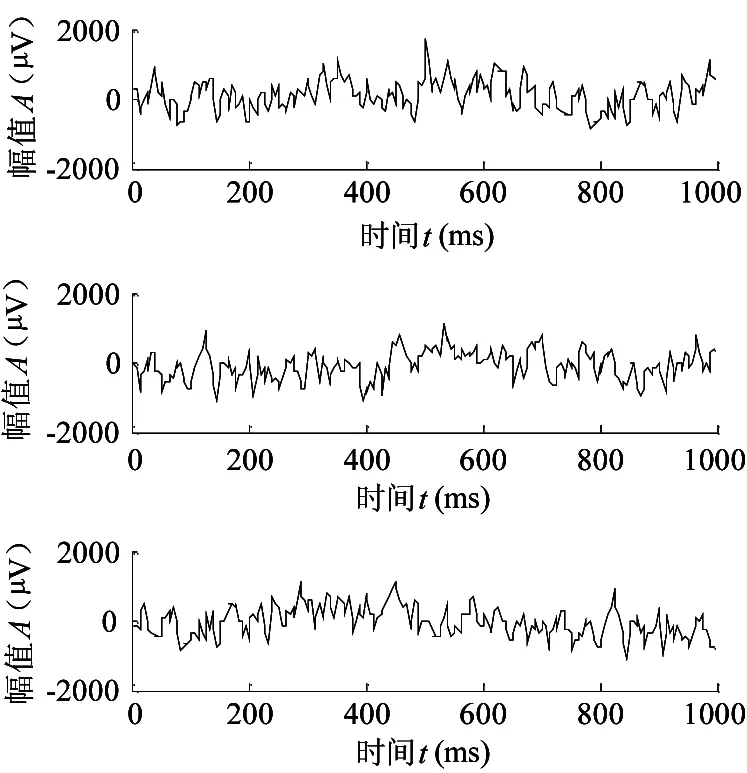
图2 原始EEG信号

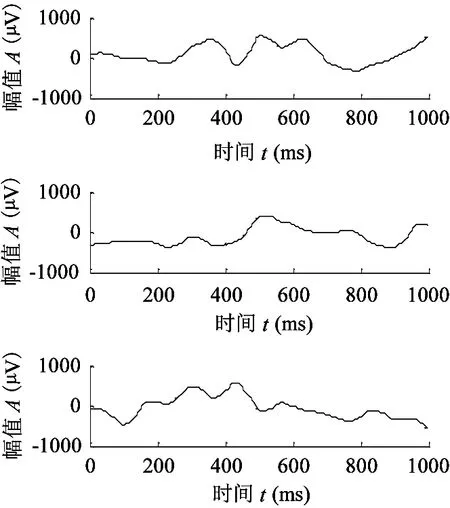
图3 频域滤波后的EEG信号

P300脑电信号与外界刺激之间具有良好的锁相关系，其波形不会因重复试验而发生很大改变，通常可采用40～100次累加平均来提高P300成分的信噪比。为便于比较分析，随机选取40组经过频域滤波的靶刺激信号进行累加平均，将其作为标准信号，如图4所示。将上述3组经过频域滤波的靶刺激信号进行累加平均，将其作为参考信号，如图5所示。

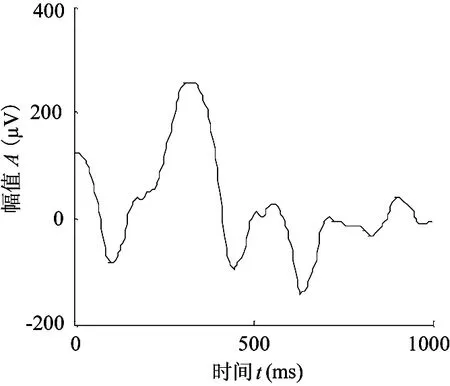
图4 标准信号-40试次累加平均

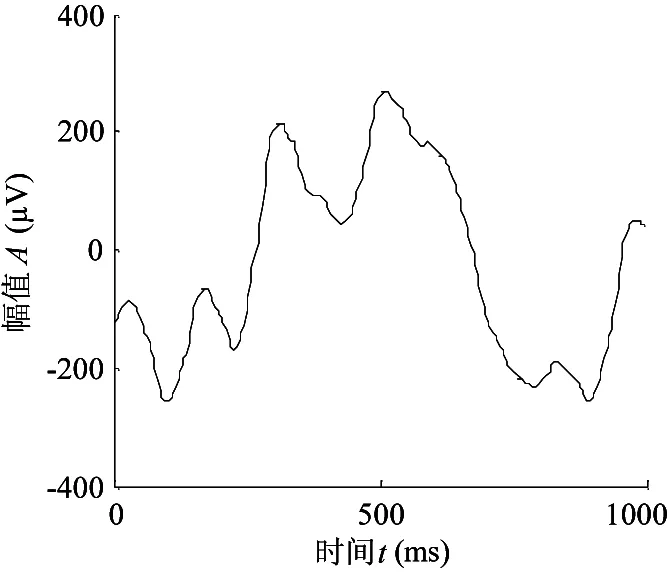
图5 参考信号-3试次累加平均

2.2 基于盲源分离JADE算法的特征提取

经过小波变换子带重组的多通道输出信号中，P300成分得到显著增强，非目标信号得到有效削弱，可以认为小波变换后的观测信号由3个信源组成，分别为P300、自发EEG以及噪声干扰，因此应用JADE算法对3试次信号进行盲源分离，能够有效估计出相对较强的P300成分[10]。对前述经过频域滤波后的3组靶刺激信号进行JADE盲源分离，得到3个源信号的估计分量，可以通过如下两种方法来提取其中的P300分量：

(1) 相关系数最大化

样本变量X、Y间的皮尔逊相关系数(Pearsom correlation coefficient, PCC)定义为

(1)

将得到的3个源信号的估计分量分别和靶刺激标准信号作相关分析，相关系数最大的即为P300分量。但是，由于观测信号均为单导联单次试，对非靶刺激来说，任一个观测信号含有大量的P300成分，就会导致分离得到的其中一个估计分量的相关系数较大，导致判断错误。

(2) 列项标准差最小化

混合矩阵的列向标准差定义为[11]

(2)

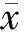
盲源分离中分离矩阵W的逆矩阵H的列反映了源信号在各观测信号中的变化情况，P300成分相对稳定，变化差异较小，其对应的混合矩阵H的列向标准差较小。对H的3个列向量依次作列向分析，标准差最小的即为P300分量。但是，由于自发EEG和噪声干扰的随机性和不稳定性，其对应的列向标准差最小的情况也是可能存在的。

针对上述问题，本文利用层次分析法，构建了一个具有丰富层次结构的分析评价模型，将从源信号的估计分量中有效、准确地提取P300分量转化为一个最优化选择问题，其实质就是依据相关系数及列项标准差，选择一个最有可能是P300分量的部分。根据层次分析原理[12]，最高层次A即为P300分量的相似程度；第2层次B包含2个一级评价指标，列向标准差B1和相关系数B2；对于第3层次C，为便于计算，将列向标准差小、中、大分别定义为3个二级评价指标C1、C2、C3，将相关系数大、中、小分别定义为3个二级评价指标C4、C5、C6，依据表1中的1～9比较尺度构造各层次的判断矩阵，如表2～4所示。

表1 判断矩阵标度及其含义

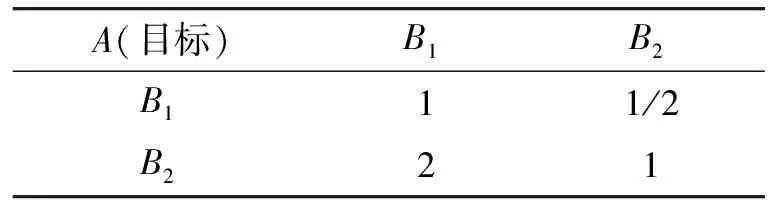
表2 一级评价指标判断矩阵

表3 列向标准差层次下二级指标判断矩阵

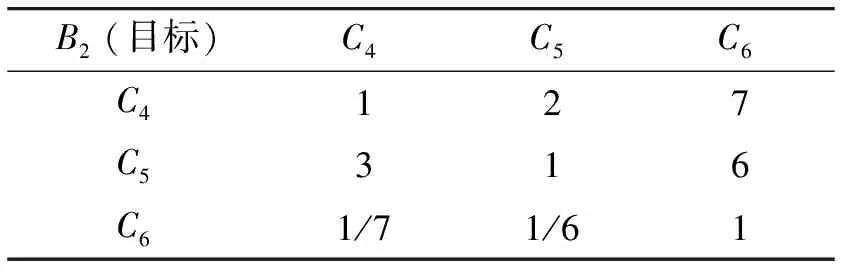
表4 相关系数层次下二级指标判断矩阵

求解各判断矩阵的特征向量，对一级评价指标、二级评价指标的权重进行计算，得到列向标准差B1的权重为0.333，相关系数B2的权重为0.667，C1～C6的权重分别为0.635、0.287、0.078、0.582、0.348、0.070，且判断矩阵均满足一致性准则。依据以下步骤对P300分量进行最优提取：

(1) 依据式(2)，对混合矩阵H的3个列向量做列向分析，得到标准差序列σ1、σ2、σ3，按数值大小分别对其重新赋值为相应的权重C1～C3；

(2) 依据式(1)，将3个源信号的估计分量分别和靶刺激标准信号作相关分析，得到相关系数序列ρ1、ρ2、ρ3，按数值大小分别对其重新赋值为相应的权重C4-C6。

(3) 依据式

Wmax=max{B1×σi+B2×ρi}， i=1,2,3

(3)

权重最大值Wmax所对应的估计分量即为所要提取的P300分量。式中，权重最大值可取为0.600、0.484、0.444或0.414。根据上述方法选择出P300分量后，将其余代表自发脑电和噪声干扰的分量置零，利用混合矩阵对其进行重构，完成对脑电信号P300成分的特征提取。

2.3 基于时域能量熵和小波变换的时频补偿

根据信息论中香浓熵的概念，定义时域能量熵

Ei=-log(Pi/P)

(4)

式中，Ei为第i段信号的时域能量熵，Pi为第i段信号的能量，P为信号的总能量。时域能量熵的大小描述了信号能量在时域上的分布情况：能量熵大，对应的时域段能量在信号总能量中的比重小；反之，在信号总能量中的比重大。

对前100，200，…，1200试次频域滤波后的靶刺激和非靶刺激EEG信号分别进行累加平均，把得到的12个信号分别分割成20段，每段50ms，包含12个数据点，进行时域能量熵分析，如图6、图7所示。

图6 靶刺激时域能量熵值的统计分布

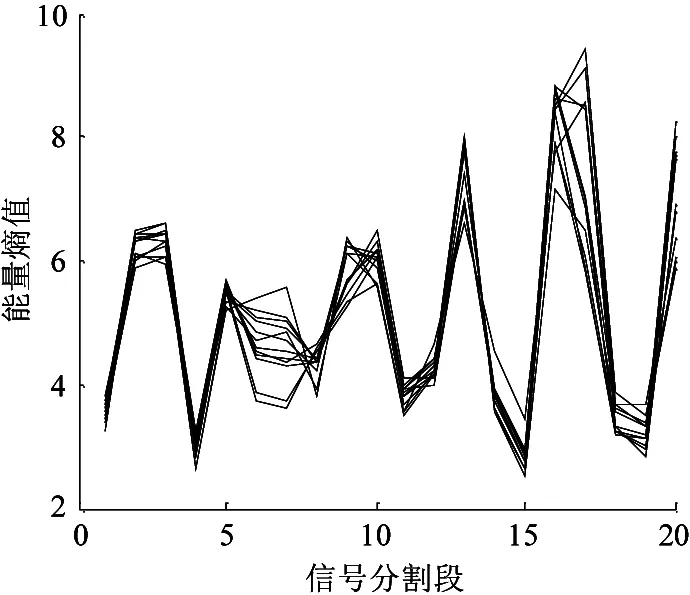
图7 非靶刺激时域能量熵值的统计分布

从图中可以看出，靶刺激和非靶刺激时域能量熵的分布具有统计特性，而且差异性显著，靶刺激信号在300ms左右的时域段能量较为集中，非靶刺激信号在整个时域上的能量分布较为平均。分别对20段的时域能量熵值进行处理，每段靶刺激和非靶刺激的各12个数据中，去掉2个最大和最小熵值，求出剩余的8个数据中的极大和极小熵值，这样对于每一个段即产生靶刺激最大、靶刺激最小、非靶刺激最大和非靶刺激最小4个阈值，分别选择其中的最大和最小熵值作为门限阈值，如表5所示。

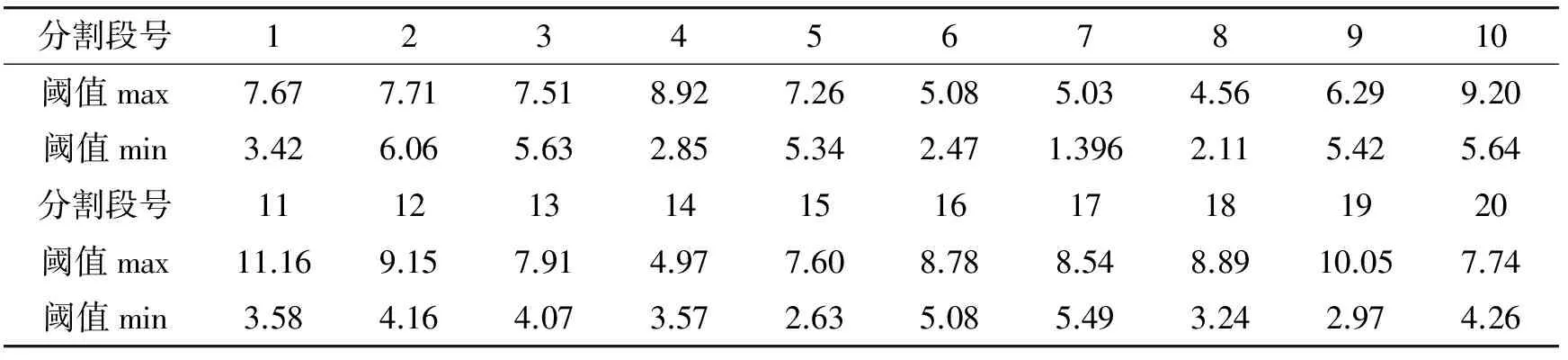
表5 时域能量熵门限阈值分布表

如图8、图9所示，利用时域能量熵的统计分布特征对重构后的信号进行补偿，具体步骤如下：

(1) 对每一个重构后的脑电信号进行时域能量熵处理，选择门限阈值之外距离最远的6段作为调整段。

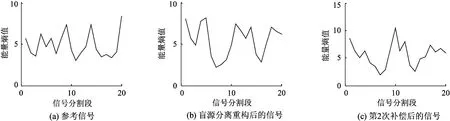
图8 经过时频补偿后的时域能量熵值分布

图9 经过时频补偿后的时域分布

(2) 对其中较远的5个调整段重新赋值为门限阈值，根据总能量P不变的等式求出第6个调整段调整之后的熵值。

(3) 利用Daubechies8小波，按照前述小波变换的频域滤波方法，对调整之后的信号作平滑处理，完成第1次补偿。

(4) 若补偿后信号某一段的幅值超过400μV，则将该段的数据还原为调整前的大小，再次做平滑处理，完成第2次补偿。

3 试验结果及数据分析

3.1 靶刺激单导联P300少试次提取相关程度分析

由于P300信号的潜伏期为300ms左右，因此这里只对前500ms内的信号作相关分析处理。上述参考信号、经过盲源分离JADE算法提取并重构后的信号、第1次补偿后的信号、第2次补偿后的信号与标准信号的皮尔逊相关系数(PCC)依次为0.490、0.670、0.663和0.887，由此可见，经过本文算法提取的靶刺激P300成分与标准信号高度相关。这里第1次时频补偿后相关系数较低主要是由于较大的波峰或波谷导致。

为进一步说明本文算法的有效性，在MATLAB R2010b Win32平台下，随机选取100组靶刺激信号作分析处理，并对重构后PCC系数小于0.7的信号作时频补偿。如图10、表6所示，依据本文算法，在导联数量和试验次数均较少的情况下仍能获得较高的相似程度，相比于累加平均、盲源分离等方法有很大程度的提高。

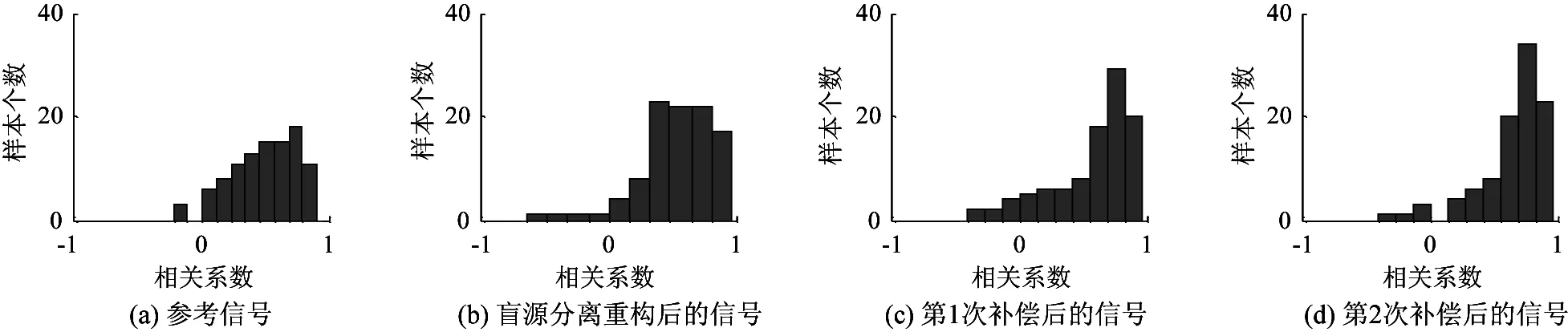
图10 提取的P300成分与标准信号相关系数试验次数的统计分布对比

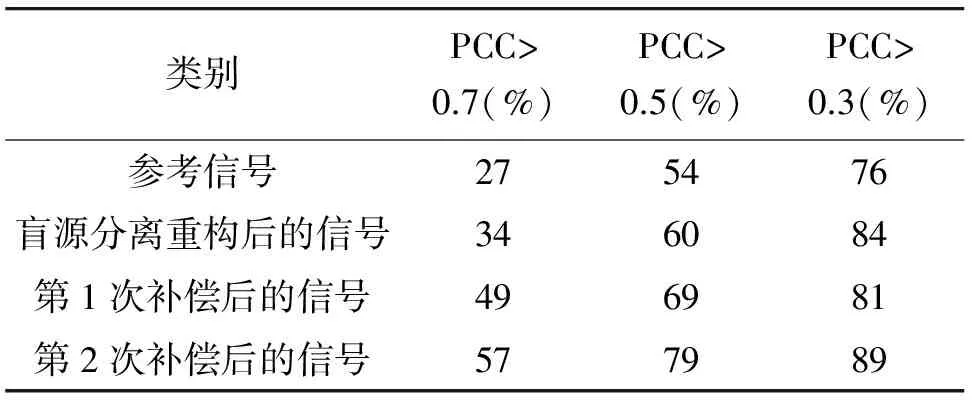
类别PCC>0．7(%)PCC>0．5(%)PCC>0．3(%)参考信号275476盲源分离重构后的信号346084第1次补偿后的信号496981第2次补偿后的信号577989

3.2 靶刺激、非靶刺激单导联P300少试次提取效果对比

如图11所示，本文算法所提取的靶刺激、非靶刺激信号中的P300成分，相比于3试次累加平均和经过盲源分离重构后得到的结果，靶刺激波形相对于非靶刺激波形的P300成分更加明显，更加接近于标准信号。

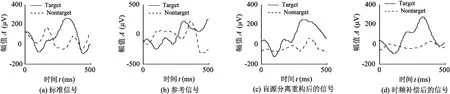
图11 靶刺激、非靶刺激信号提取P300成分的效果对比

4 结 论

P300脑电信号作为事件相关电位(ERP)中重要的内源性成分被广泛应用于脑-机接口(BCI)系统中，但是临床上使用的ERP检测仪器均采用累加平均技术，忽略了不同试次之间的差异性和多试次引起的神经性疲劳，造成操作繁琐、数据冗杂等问题。本文提出的单导联脑电信号P300少次提取算法，在采用小波变换与盲源分离JADE算法作滤波处理的同时，利用层次分析模型提取其中的P300分量，有效避免了少次提取中可能存在的突发性错误对提取结果造成的影响，并采用时域能量熵的统计分布特性对重构后的信号进行时频补偿，进一步强化P300特征成分。本文方法在单通道、3试次的情况下，仍能够有效地提取EEG中的P300成分，而且有效克服了多导联、多试次产生的缺陷，为基于P300脑电信号的BCI系统在线应用打下基础。

[1] Tu Y, Hung Y S, Hu L, et al. An automated and fast approach to detect single-trial visual evoked potentials with application to brain-computer interface.ClinicalNeurophysiology, 2014, 125(12): 2372-2383

[2] 郭凯, 裴为华, 王宇等. 基于干电极的头带式射频无线脑-机接口系统. 高技术通讯, 2012, 22(2): 211-216

[3] 程龙龙, 邱爽, 徐瑞等. 基于极能差与共空间模式的脑电信号特征增强研究. 高技术通讯, 2013, 23(9): 980-987

[4] Postelnicu C C, Talaba D. P300-based brain-neuronal computer interaction for spelling applications.IEEETransactionsonBiomedicalEngineering, 2013, 60(2): 534-543

[5] Vareka L, Mautner P. Off-line analysis of the P300 event-related potential using discrete wavelet transform. In: Proceedings of the 36th International Conference on Telecommunications and Signal Processing, Rome, Italy, 2013. 569-572

[6] Mousavi S A, Arshad M R H M, Mohamed H H, et al. P300 detection in electroencephalographic signals for brain-computer interface systems: a neural networks approach.ComputerEngineeringandNetworking, 2014, 277: 355-363

[7] Elsawy A S, Eldawlatly S, Taher M, et al. A principal component analysis ensemble classifier for P300 speller applications. In: Proceedings of the 8th International Symposium on Image and Signal Processing and Analysis, Trieste, Italy, 2013. 444-449

[8] 艾玲梅, 李营, 马苗. 基于EMD和PCA的P300分类算法. 计算机工程, 2010, 36(5): 182-184

[9] Wessel J R, Ullsperger M. Selection of independent components representing event-related brain potentials: a data-driven approach for greater objectivity.NeuroImage, 2011, 54(3): 2105-2115

[10] 黄璐, 王宏. 单导联脑电信号P300分类研究. 仪器仪表学报, 2014, 35(4): 814-819

[11] 陈洪波, 李蓓蕾, 陈真诚. 基于ICA的脑电信号P300少次自动提取. 电子学报, 2012, 40(6): 1257-1262

[12] Ishizaka A, Labib A. Review of the main developments in the analytic hierarchy process.ExpertSystemswithApplications, 2011, 38(11): 14336-14345

Study on extraction of P300 from monopolar lead EEG signal using several trials

Hu Chunhai， Xin Sixu， Liu Yonghong

(Measurement Technology and Instrumentation Key Lab of Hebei Province,Yanshan University, Qinhuangdao 066004)

The extraction of the positive potential P300 from electroencephalography (EEG) signals was studied. To vercome P300 extraction’s harsh requirements in electrode number and trial times, a new method for extraction of P300 from monopolar lead EEG signals using several trials was proposed. The method removes the noises in original signals by using wavelet transform and uses the Joint Approximate Diagonalization of Eigenmatrices (JADE), algorithm for blind source separation to decompose the observed signals, then, performs the optimal P300 extraction by using the analytic hierarchy process model built according to the pearson correlation coefficient (PCC) and the column standard deviation to avoid the possible sudden errors in P300 extraction in several trials, and finally, uses the statistical properties of temporal energy entropy and the wavelet transform principle to compensate reconstructed P300 signals in the time and frequency domain. As shown by the experimental results, only three trials of monopolar lead data need to be processed with the proposed method, and the P300 ingredient was extracted more effectively.

EEG processing, P300, temporal energy entropy, wavelet transform, analytic hierarchy process model

10.3772/j.issn.1002-0470.2016.04.006

①国家自然科学基金(61201110)资助项目。

2016-03-14)

②男，1966年生，博士，教授；研究方向：视觉检测技术，信息融合，脑机接口等；联系人，E-mail: fred-hu@ysu.edu.cn(