横向气流中非牛顿液体射流直接数值模拟
2016-12-06朱呈祥尤延铖
朱呈祥*,尤延铖
厦门大学 航空航天学院,厦门 361005
横向气流中非牛顿液体射流直接数值模拟
朱呈祥*,尤延铖
厦门大学 航空航天学院,厦门 361005
采用直接数值模拟研究了动量比为6的非牛顿液体射流在横向气流中的破碎特征,重点分析了表面波发展、弯曲特性和展向扩散等射流结构及其非牛顿特征。在非牛顿液体射流的近喷嘴位置,其表面迹线随时间摆动,并有逆横向气流方向运动的趋势。射流的展向扩散仅在喷入初期较为明显,此后基本维持在接近35°的扩散半角。射流的一次破碎,尤其是液丝与液滴、甚而卫星液滴的生成过程都被精细地捕捉和描述。在近喷嘴的射流柱附近,横向气流流动具有一定的圆柱扰流相似性,在其他区域则表现为极其复杂的紊流特征。射流的非牛顿特性主要体现在黏性系数,不同位置的液体黏性系数相差超过20%。相较牛顿液体射流,剪切稀化的非牛顿射流具有更易破碎的特征。
液体射流;横向气流;非牛顿流体;破碎;直接数值模拟
液体射流喷入横向气流被广泛应用在工程实际中,包括发动机的液体燃料喷注、农业灌溉、喷墨打印等,深入理解液体射流的物理本质对开发高效率的此类设备至关重要。
目前国际上针对液体射流喷入横向气流已经开展了大量研究。在实验领域,Lee[1]和 Sallam[2]等分别对比了不同湍动进口条件下和非湍动进口时圆形液体射流在横向气流中的喷入特征;Birouk[3]、Wu[4]和Stenzler[5]等则进一步整理了液体射流喷入横向气流后的发展规律,包括射流的破碎模式、喷射轨迹、穿透深度、破碎长度等。此外,Gutmark[6]、Shapiro[7]、Megerian[8]和 Coletti[9]等针对射流在横向气流中的破碎特征也都开展了相关的实验研究。
在数值领域,Herrmann[10-11]以力平衡优化水平集(Balanced Force Refined Level Set)方法为基础,重点对比了不同气液两相密度比下的射流破碎特征,Cavar和 Meyer[12]则运用大涡模拟(LES)技术探究了射流的涡场结构。与Cavar和Meyer的研究类似,Galeazzo等[13]也主要关心涡的形成发展,但其重心偏向于气液两相的掺混。在针对液体射流喷入横向气流的参数研究中,Sau和Mahesh[14]根据雾化水平专门对液体射流的喷入条件进行了优化,Pai等[15]则将重心放在流量比和气流韦伯数上,比较了它们对射流特征的影响,Muldoon和Acharya[16]则从力学角度出发,分析了不同简谐力下横向气流中的射流结构。此外,Margason[17]、Aalburg[18]和 Mahesh[19]等还分别对目前该领域的国际前沿工作进行了整理总结。
前文提到的所有研究都只考虑了牛顿流体。在非牛顿流体方面,Wong等[20]重点分析了4种不同的射流破碎类别,并比较了最终的破碎长度和液滴尺寸。Clasen等[21]则对一类黏弹性流体开展了实验研究,并着重分析了它的稀化特性。此外,Yarin[22]还专门针对非牛顿流体的力学和流变特性进行了总结。然而到目前为止,国际上还没有针对非牛顿流体开展过射流在横向气流中的研究。但在工程实际问题中,非牛顿流体其实广泛存在,以液体燃料为例,通常将其简单处理为牛顿流体,但事实上在添加了稳定剂和抗氧化剂后,液体燃料是具有弱的非牛顿特性的。而在液体火箭发动机中,甚至需要采用高黏度的剪切稀化非牛顿流体作为燃料,以应对它的储存问题。这些将直接导致其破碎体系相较传统煤油更为复杂,并最终诱发不同的雾化效果与燃烧效率。
因此,本文将以非牛顿流体为研究对象,开展直接数值模拟(Direct Numerical Simulation,DNS)研究,重点分析液体射流在近喷嘴附近的流动特征。介绍采用的数值方法与设置,重点分析液体射流的三维结构、弯曲和扩散特性、时域变化、涡场特征等,讨论其非牛顿黏性变化,并与牛顿射流进行对比。
1 数值方法

本文采用的数值工具为自主开发的DNS程序Free Surface 3D(FS3D),该程序求解的是三Δ维不可压Navier-Stokes方程组:式中:u为速度矢量;ρ为密度;p为压力;t为时间;k为外部作用力;T为气液两相分界面处的表面张力。FS3D程序采用流体体积(Volume of Fluid,VOF)[23]方法捕捉气液两相分界面,该方法定义变量f表征单元格内的液体体积分数,即

f满足以下守恒关系:

为了精确描述气液两相分界面,FS3D程序还运用分段线性界面计算(Piecewise Linear Interface Calculation,PLIC)[24]方法进行了分界面重构。此外,模拟射流进口的湍流度对工程应用同样至关重要,因此FS3D程序还搭建了一个基于Kornev和Hassel[25]的来流发生器。相应的数值方法均已在文献[26-27]中进行了气液两相液滴和瑞利破碎射流的实验验证,也说明了方法的可靠与准确性。

对于非牛顿黏性,本文采用以下的幂律函数进行模拟:
式中:μ0为零剪切时的动力黏度为剪切率;K和n为取决于流体和环境的模型常数。该幂律模型已被 Motzigemba[28]以及 Focke等[29]验证过。同时,文献[30]也就液态射流的黏性系数开展了基于Schroeder等[31]的实验数据的验证。
本文模拟的横向气流为空气,液体是20%质量分数的剪切稀化PVP溶液。该液体的Deborah数 De和Elasto-capillary数Ec都在10-8量级,远低于黏弹性流体的极限值0.35和2.35,因此是典型的幂律流体。
表1给出了液体与气体的相关物性参数以及射流直径D,下标l和c分别代表液体与横向气流。在横向气流射流喷注研究中,气液两相的动量比往往是决定射流流态的一个关键参数[32],本文定义气液两相动量比q为

此外,表2还给出了基于式(8)的气液两相韦伯数We与雷诺数Re:

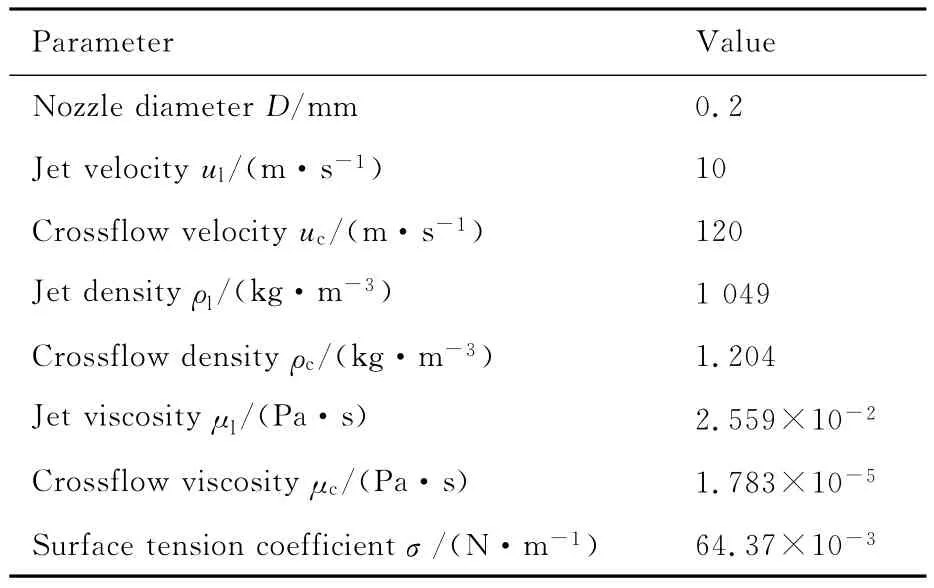
表1 计算条件设置Table 1 Computational condition setup

表2 无量纲参数Table 2 Dimensionless parameters
本文将着重分析射流在启动过程中近喷嘴附近的流动特征。这主要有两个方面的考虑,一是对于持续喷注,射流初期的流动特征对最终的流动形态影响显著,这对透彻理解射流破碎过程非常重要;另一方面,射流启动过程也是间歇喷注的主要流动特征,因此分析启动过程是研究间歇喷注的关键。为了研究射流的横向喷注,本文将采用如图1所示的矩形计算域,左侧边界面为气流入口,以恒定速度uc吹入横向来流,液体从xOy面内的圆形喷嘴喷入,横向气流沿x正方向从左侧的yOz面流入。下边界为无滑移壁面,靠近左侧边界面开有一个圆形射流入口,液体以帽状速度型读入并沿y轴正向喷入,其余边界设置为自由出流(von Neumann)条件。对于左侧的速度入口边界,直接将来流速度型赋给虚网格,不考虑液体在喷嘴内由于近壁无滑移而形成的边界层,在工程中这对应短直喷嘴。该模拟过程相当于先单独计算喷嘴流动,将其出口速度型提取出来,再赋值给本计算域直接作为边界条件读入。该手段由于无需布置过多网格在喷嘴近壁边界层内,不会导致计算资源浪费,因此在DNS中已被广泛采用。为了能够求解湍流中Kolmogorov长度[33]以满足DNS对网格精度的要求,本文在计算域10D×10D×5D内布置了512×512×256的结构化网格,因此最小网格尺度仅为4μm。

图1 矩形计算域示意图Fig.1 Schematic of rectangular computational domain
2 射流结构
图2给出了非牛顿液体喷入横向气流后近喷嘴处的流动结构。图中:t*=t ul/R,t为物理时间,ul为射流速度,R为射流半径,射流表面颜色代表无量纲速度(为当地速度除以液体射流速度)。射流沿着y轴正向喷入,横向气流沿x轴正向喷入。受横向气流的影响,液态射流沿x轴正向弯曲,并沿z轴展向扩散。随着射流深度的增加,液体被逐渐剪切成薄层,并在一定范围内与横向气流的流动方向几乎平行。然而这种平行流动的趋势在射流前部并不存在,到射流头部液体甚而逆着横向气流的方向弯曲,形成了一个大的类似bag类型的破碎,并产生了若干分裂的液丝与液滴。而这些液丝与液滴由于分裂位置不同也表现出了不同的速度分布,靠近喷嘴出口的速度低,靠近头部前缘的速度高。

图2 t*=9.2时刻的横向气流射流结构Fig.2 Flow structure of jet in crossflow(t*=9.2)
虽然 Hermann[10]也曾在相似的动量比 (q=6.6)下开展过横向射流数值计算,但本文发现的上述流动特征与其存在显著区别。这主要有两个原因:一是无量纲参数的差别,二是本文选用了非牛顿剪切稀化流体。在无量纲参数方面,尽管Her-mann教授与本文选用的q相似,但他采用的Re和We却很高。Pai等[15]曾指出,即使采用相同的q,液体韦伯数Wel的不同同样会产生不同的射流结构。在非牛顿流体和牛顿流体方面,液体的零剪切黏性系数较高将削弱射流的破碎;在射流内不同剪切率的位置,液体由于黏性系数不同也会表现出不同的破碎形式,射流的破碎也将最先发生在剪切率较高的区域。在以上两个原因共同作用下,本文研究的液体射流形成了前文提及的类似bag类型的流动与破碎特征。
为了更好地观察横向气流中非牛顿射流的结构,图3分别给出了液体的前视与俯视图,图中红色箭头代表射流方向,蓝色箭头代表横向气流方向,黑色实线为射流的弯曲轨迹,并与 Wu[4](红色实线)和Stenzler[5]等(蓝色实线)进行对比。从图3(a)可以更明显地看出射流的弯曲特性,但与 Wu[4]和Stenzler[5]等拟合的弯曲曲线相比,本文研究的射流弯曲轨迹明显偏低。Wu在拟合曲线的过程中主要考虑了横向射流的力学特性,在多种牛顿流体(水、乙醇、丙三醇等)和宽参数范围(如动量比3.38<q<185)基础上推导射流的弯曲轨迹。他指出,射流的弯曲轨迹主要由两个因素决定,一个是动量比q,另一个就是液体的黏性系数。在他们的研究中,液体最高的黏性系数约为水的3.66倍,这明显低于本文研究的25倍水黏性系数。Wu在文献[4]中也对比了不同黏性系数流体的横向射流,他强调,高黏性系数液体射流会比低黏性系数液体射流的弯曲程度更高,这正与本文得到的射流结构是相吻合的。当然,由于本文采用的是剪切稀化非牛顿流体,而Wu所研究的均为牛顿流体,因此Wu所提到的高黏性效应会被一定程度削弱。此外,文中仅考虑射流启动过程的弯曲特性,这与 Wu[4]和Stenzler[5]等的持续喷注也存在区别。
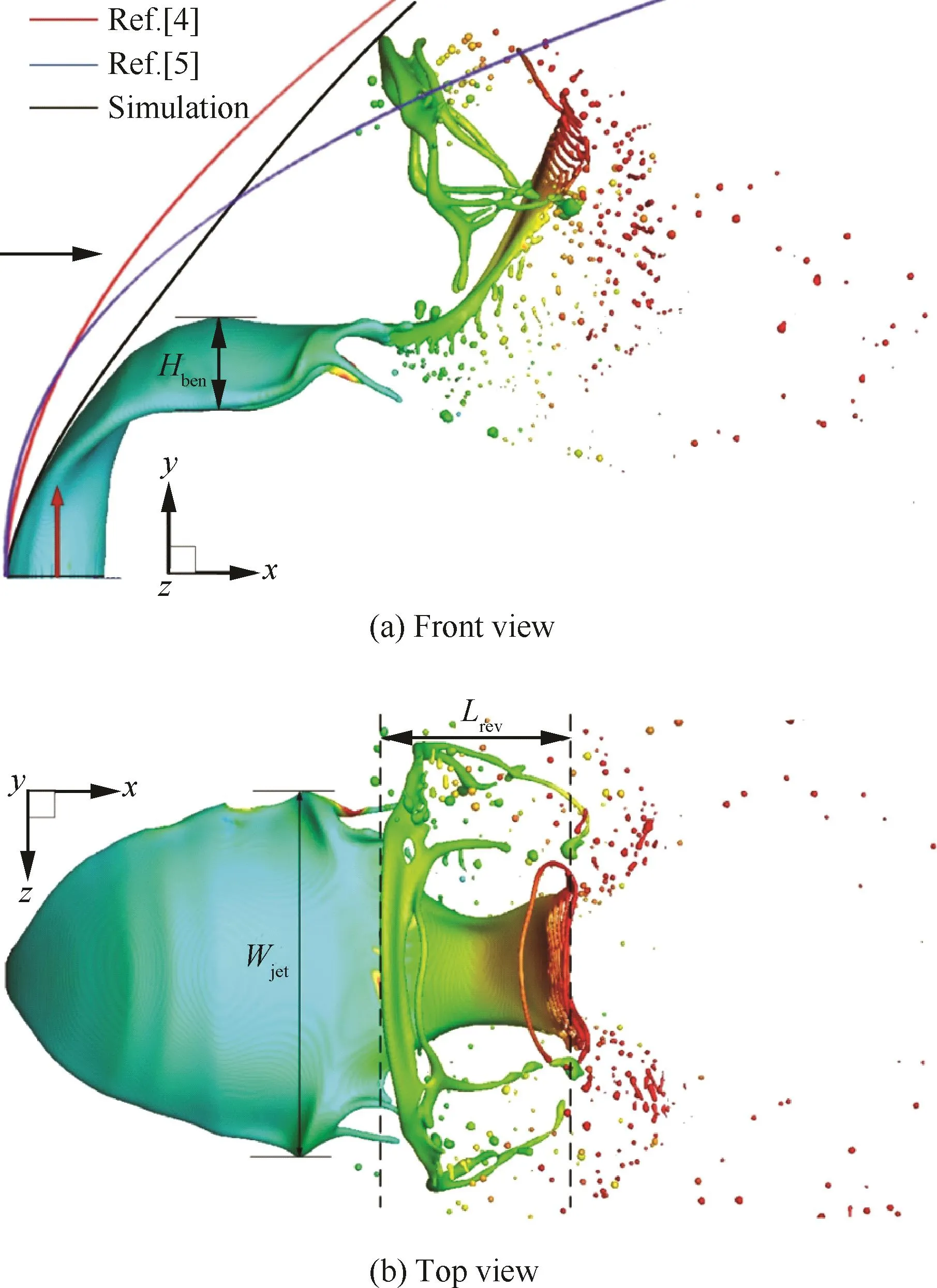
图3 射流结构的前视图和俯视图Fig.3 Front view and top view of jet structure
从图3还可以发现,射流不仅沿x轴方向弯曲,而且在y轴方向也存在弯曲,以轴向位置x/D=2D处为例,液体向下弯曲(y轴负方向)的高度Hben达到了0.875D。在图3(b)中,射流沿z方向的展向扩散现象也非常明显。随着轴向位置的增加,液体的宽度Wjet也逐渐增加,x/D=2.9D处射流的宽度达到了3.5D。在该图中,前文提到的射流头部逆横向气流现象也更为显著,射流逆向区域的长度Lrev(定义为下游未破碎区到逆向头部前缘的x轴的距离)达到了1.875D。结合图3还可以发现,射流破碎主要发生在薄层区(也称为表面破碎),这是由于该区域内液体被最大程度地剪切,因此黏性系数也最低。射流在该时刻形成的液滴尺寸覆盖了D/8~D/40之间,其中圆形液滴的尺寸主要集中在D/10~D/15。射流分裂的位置不同,各小液滴的运动速度也不尽相同,最快的液滴速度甚至可以超过最慢液滴的4倍。
图4为射流的总面积S*与总质量m*随时间的变化关系,这里的面积与质量均为无量纲参数,无量纲关系为

式中:射流的表面积总体上随时间增加,具体可划分为3个主要区间。t*<t*1=3时,由于射流仅轻微波动,表面积缓慢增加;t*>t*1时,射流开始出现弯曲并被剪切成薄层,因此表面积快速增加,到t*2=8时表面积已经达到了5;当t*>t*2时,面积增加开始放缓,此时液丝与液滴的生成是面积增加的主要因素,但这种面积的增加相较液体薄层引起的面积增加是少量的。从图4(b)可以发现,当t*>t*3=8.6时液体质量出现突降,这是由于部分液体已经流出了计算域,而在此之前,液体的质量几乎恒定。
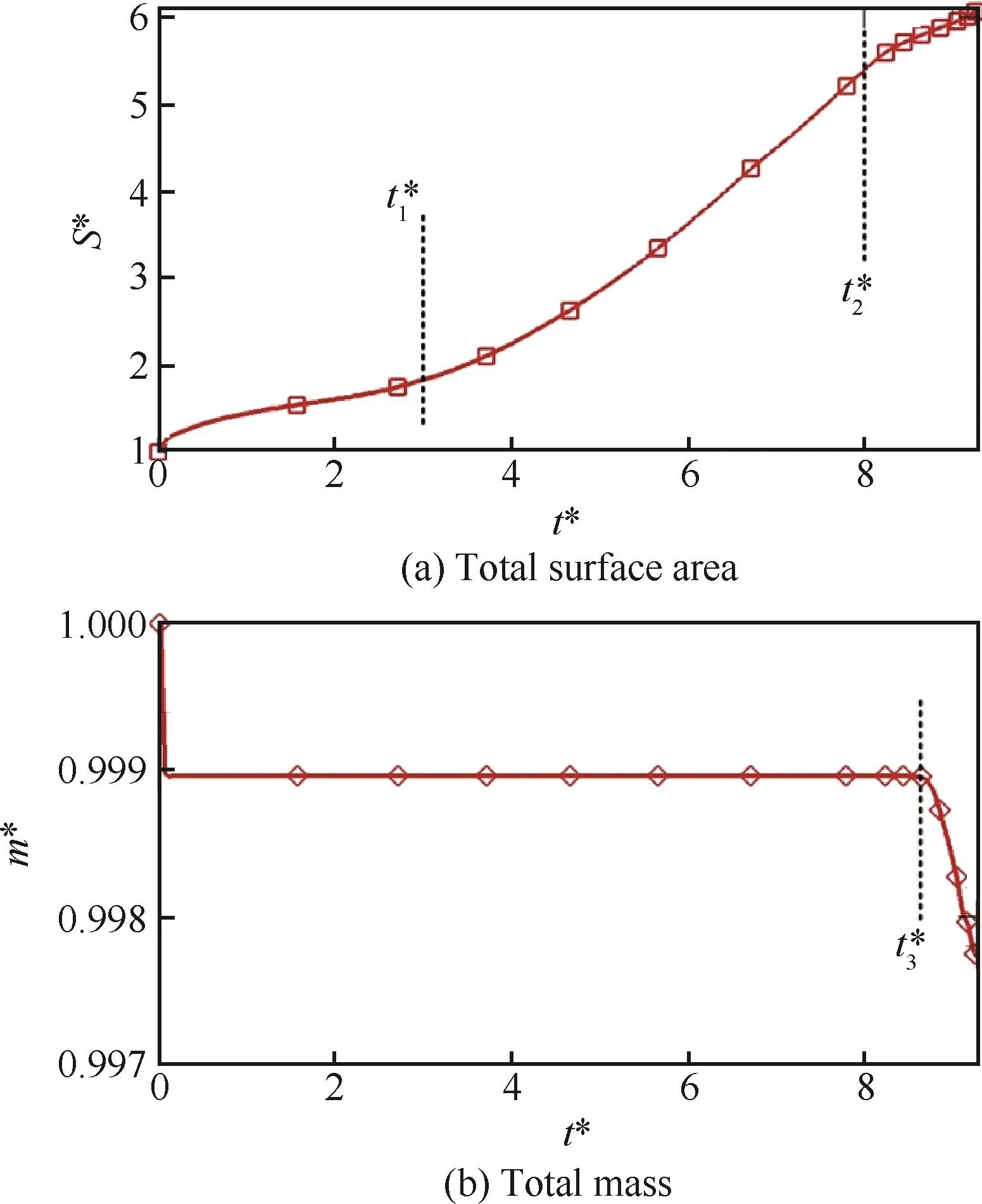
图4 射流的总面积与总质量随时间的变化Fig.4 Temporal evolution of total surface area and total mass of jet
3 特征分析
3.1 弯曲特性
液体射流在横向气流的喷注研究中,弯曲特性是其最重要的特征之一。图5给出了射流在7个典型截面内的形状,各横截面法向均与射流表面平行,内部红色区域为液体。在喷嘴出口位置,射流呈圆形,但到截面b位置时,迎风面呈平面状,这种现象在以往的研究中都未被发现过。本文将其归因于液体的高黏性系数,而与非牛顿流体无关。为了证明这一点,本文在3.5节也开展了高黏性系数的牛顿流体计算,发现其同样存在平面状迎风面。在以往的实验研究中,如文献[4-5],受实验设置的限制,很难观测到射流的瞬时横截面形状;而在数值研究中,如文献[10,18],由于液体的高黏性系数会引起气液两相分界面处物性参数的急剧跳动,因此也很难做到该类数值模拟。当然,这种前平后凸的横截面形状仍有待通过以后的实验去进一步验证。
在下游截面c,由于边缘受到的剪切较中心区域高,因此射流的迎风面形状逐渐弯曲,这种特征在截面d内更为明显。在截面e~g内,射流被逐渐拉成薄层,而且由于射流破碎,薄层的宽度逐渐减小。值得注意的是,在截面f与g内,受横向气流作用影响,液体薄层的边缘向下弯曲,极大地影响非牛顿液体的黏性,这将在3.5节中进一步讨论。
在研究射流的弯曲特性时,除了单一时刻(t*=9.2)横截面内的射流形状,本文还对比了近喷嘴处的射流弯曲轨迹,如图6所示。在t*=3时,射流向下游略弯曲,受横向气流影响,在射流前缘形成了一个小的头部。到t*=5时,该头部被拉长并沿x轴方向弯曲,形成了一个表面凹坑。该凹坑显然对横向气流更为敏感,因此在t*=7时液体被进一步拉伸剪切。在t*=7和t*=9.2之间,射流头部被快速拉长,并形成了独特的“甩尾”现象,该过程极为迅速,从t*=7~9.2,射流的轴向长度增加了一倍,即从2.7D~5.7D。从图6中还可以发现,射流头部受气流作用已出现破碎。

图5 t*=9.2时刻的射流横截面形状Fig.5 Slice view of cross-section shape of jet at t* =9.2
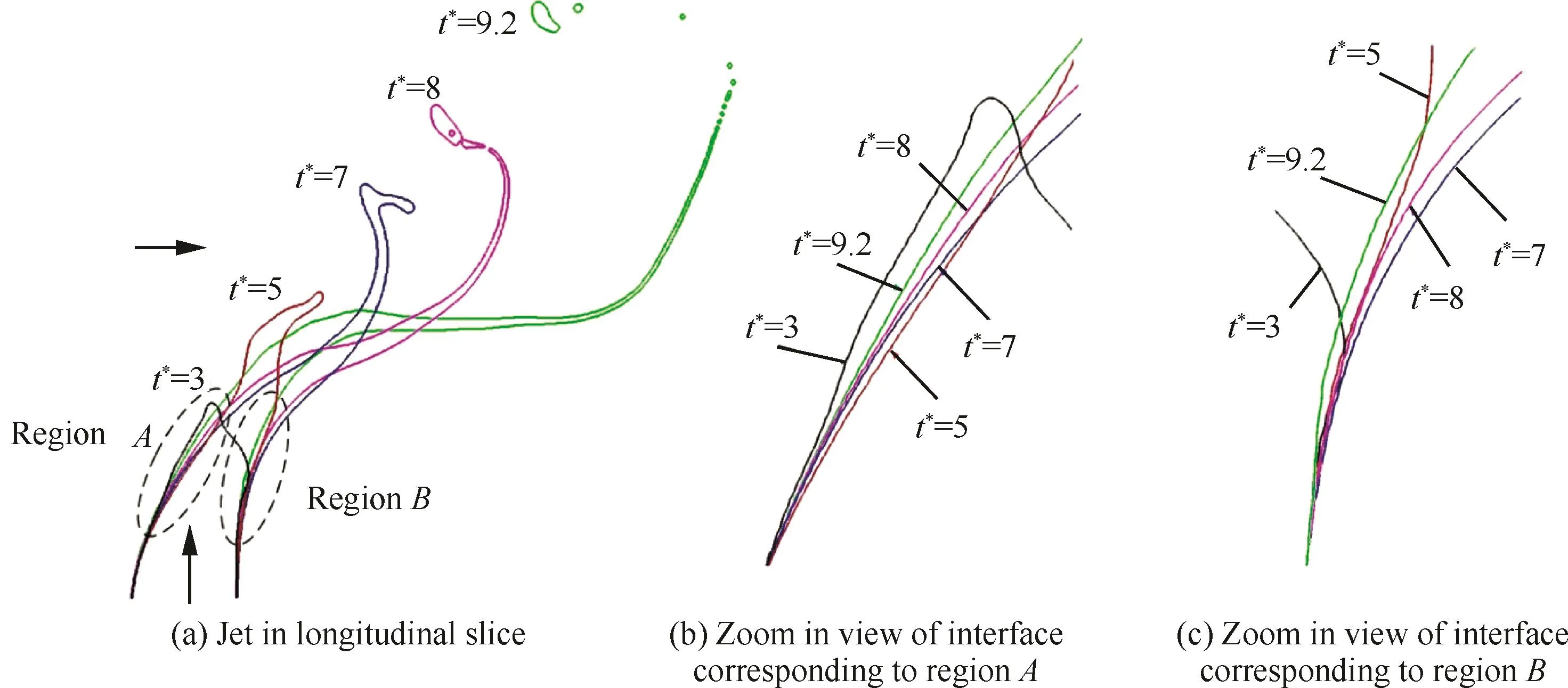
图6 对称切面内的射流随时间变化Fig.6 Temporal evolution of a jet in longitudinal slice through jet center
3.2 展向扩散特性
除了具有弯曲特性,液体在横向气流中的喷注也随时间展向扩散,图7给出了射流在4个不同时刻迎风面的左视图,虚线代表射流中心线,黑实线与α共同表征射流扩散角。此处的扩散角α定义为射流中心线与最左侧未破碎极限之间的夹角。与t*=3时相比,t*=5对应的展向面积明显增宽,并在t*=7时进一步扩散,此时射流两侧边缘由于强气流剪切已经出现破碎现象,气流剪切强意味着液体的黏性系数低,因此相较其他位置更易破碎(该破碎过程将在3.3节详细解释)。在t*=9.2时,射流出现了高度破碎,形成若干小液滴,但扩散角并未出现太大变化。
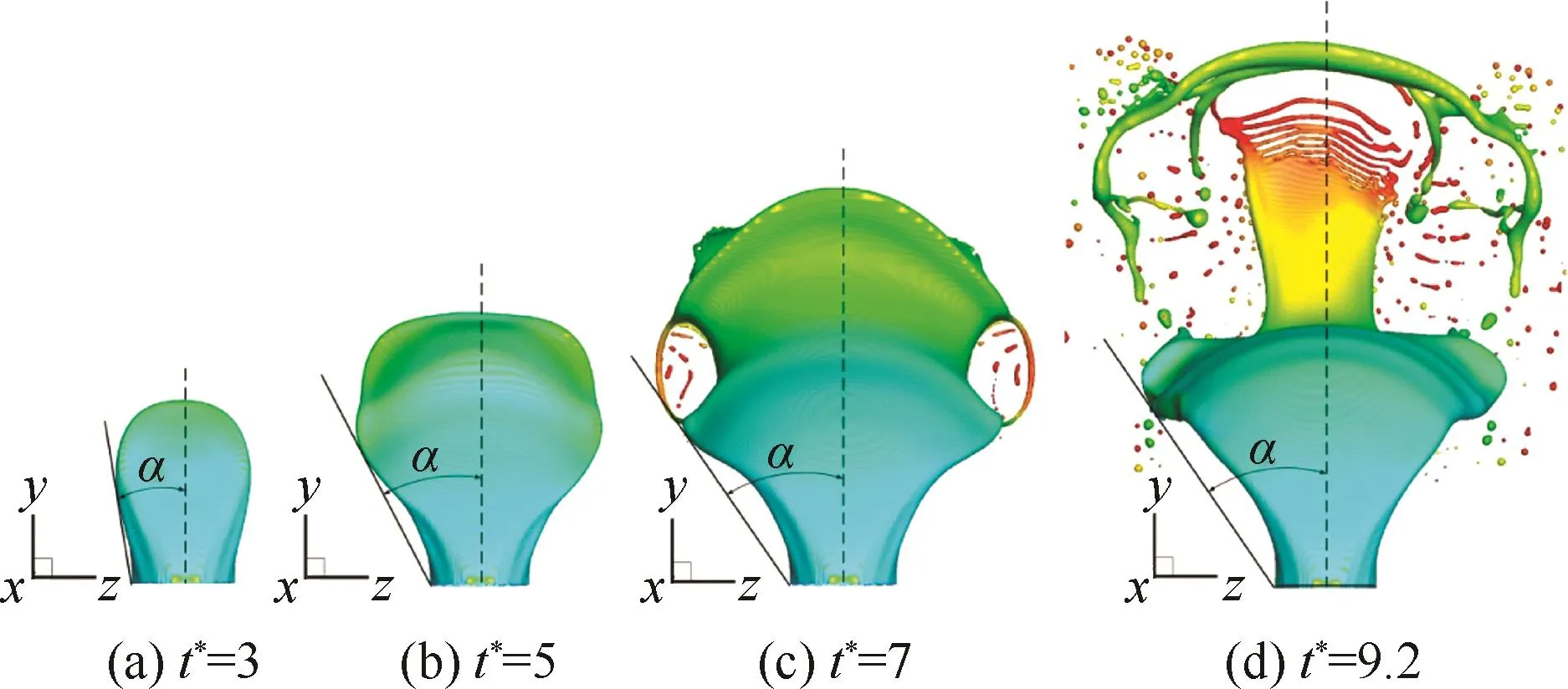
图7 射流的左视结构图Fig.7 Left view of jet structure
图8是射流扩散角的时域变化,可以看到t*=3~7时,扩散角快速增加,t*=3时扩散角仅为8.7°,到t*=5时已增长3倍多,扩散角为27.1°,在t*=7时更是达到34.4°,但在此之后扩散角的增速明显放缓,t*=9.2时仍维持在34.7°。从图8可以推断,液体在横向气流中喷注所具有的扩散特性在喷入初期最为显著,随着时间增加扩散将逐渐趋于
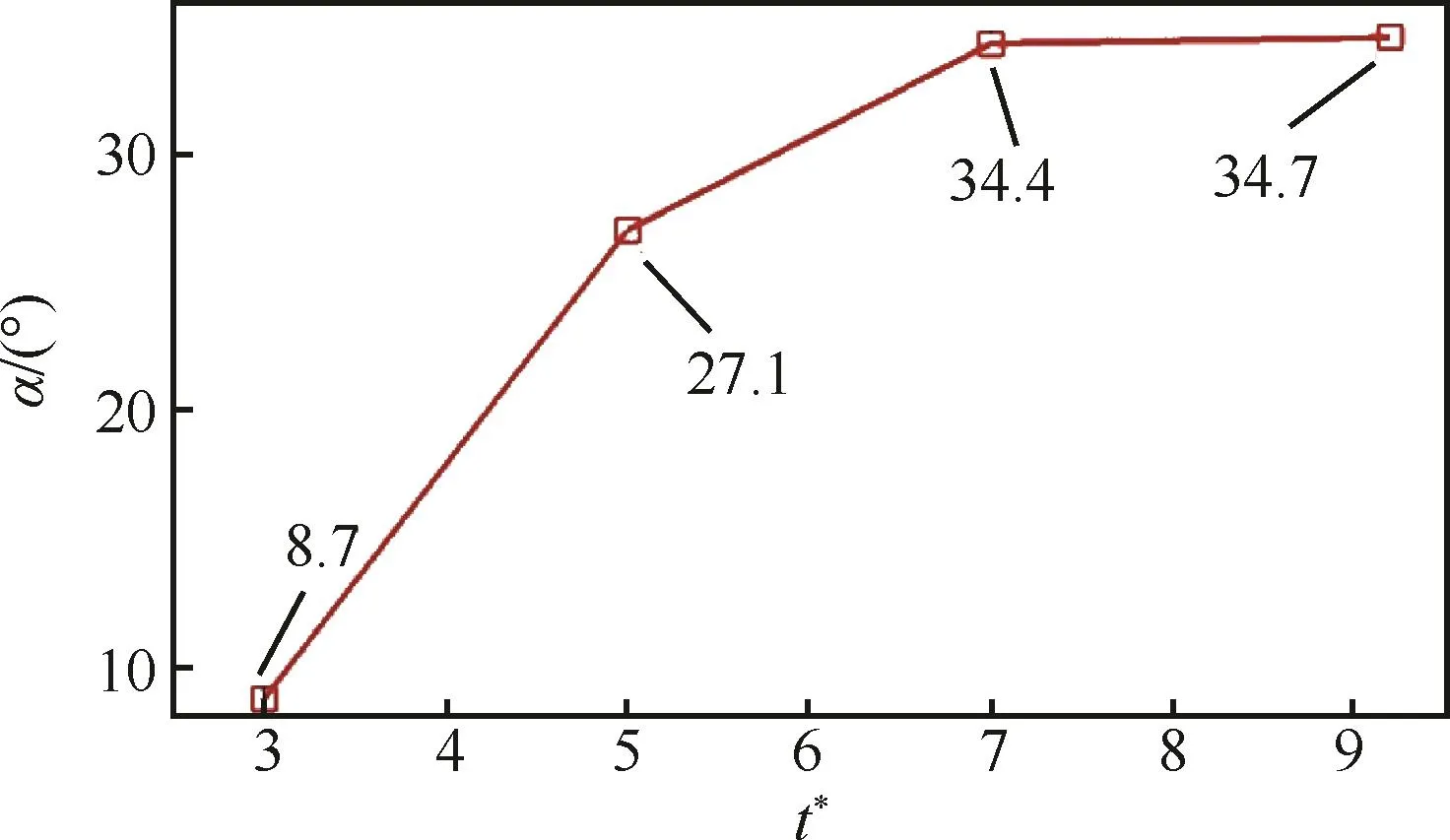
图8 射流扩散角随时间的变化Fig.8 Temporal evolution of spreading angle
稳定,这与文献[10]中在相近动量比q=6.6条件下发现的规律是类似的。
3.3 破碎特征
对于液体射流,液丝与液滴的生成无可避免。文献[4]将横向气流中的射流破碎分为两类:圆柱破碎(Column Breakup)和表面破碎(Surface Breakup),本文将重点关注如图9所示的边缘破碎,属于表面破碎类别。

图9 液丝与液滴的形成过程Fig.9 Formation of ligaments and droplets
在t*=7.6时,受表面张力作用,细长液丝的表面形成了颈部(图9(a)蓝色箭头处)。而表面张力与曲率半径成反比,即曲率半径越小受力越大,因此颈部受到的表面张力是最大的。随着时间推进,颈部将不断收缩并在t*=7.9时断裂,与此同时,液丝上形成了两个新的颈部(黑色箭头处)。相似的现象在图9(d)~图9(f)中红色与紫色箭头处同样可以看到。长液丝在横向气流的作用下变得极不稳定,颈部的形成以及最终的液丝破碎主要都是受瑞利不稳定性影响。从图9中的绿色箭头还可以发现,这些断裂后的小体积液体在表面张力的作用下有不断收缩成圆球形状的趋势。此外,图9(b)~图9(e)中黑色虚线还圈出了一个细致的液滴碰撞过程(最终同样趋于圆球形)。
3.4 涡特性
涡量分布通常用来描述当地的旋流特性。图10为本文计算得到的t*=9.2时的瞬时涡量场,白色箭头代表横向气流方向,涡量值ω根据射流直径D以及流速ul进行了无量纲处理,下标x、y、z分别代表3个方向,即

在射流的迎风面,气流中的高涡量主要集中在液体表面,并且旋流层的厚度沿着射流表面增加,近似于边界层的发展。在x/D=2.5位置,受射流弯曲影响,高涡量区将脱离液体表面,并在液体与高涡量区之间形成了一个特殊的未扰动层,同时,高涡量区在下游再贴附液体表面时形成了一个轴向漩涡(如图10(d)所示)。
在射流的背风面,存在一个非常大的高涡量尾迹区,如图10(e)所示,其涡量值范围较图10(a)大3倍。由于近喷嘴附近的射流近似为圆形,因此其流场与圆柱扰流类似。在圆柱扰流研究中,文献[34]通过对比不同来流雷诺数下单个圆柱扰流的尾迹涡发展及其阻力分布时就明确指出,当来流Rec超过40时,其扰流尾迹将出现不稳定,而本文研究中横向气流的Rec远超该临界值,达到了1 621,故出现极为复杂的尾迹区。
在射流头部附近区域M,横向气流流过液体时在下游形成了对漩涡(CVP),尽管与图10(e)同为横向扰流,但流动形态显然更加稳定,这有以下3个主要原因:①图10(b)中的液体具有x轴方向移动速度,因此气液两相的相对速度小,Rec因而也较小;②液体的尺寸较喷嘴处的射流直径小,这将进一步降低Rec;③从前缘滞止点开始沿液体表面发展的气流边界层在脱体前未完全发展,因此流动也更稳定。在图10(c)中,由于气液两相的相对速度以及液体尺寸均较小,满足涡的稳定发展条件,因此还形成了类似卡门涡街的流场结构。

图10 t*=9.2时刻的瞬时涡量场Fig.10 Instantaneous vorticity field at t*=9.2
3.5 非牛顿特征
3.5.1 黏性系数
图11给出的是射流的黏性系数(无量纲,除以μl)沿y轴的平均变化规律。可以发现,在y/D<3时,液体的黏性系数不断下降,并在y/D=3~5之间维持在一个较低值,之后又开始增加。通过分析流场可知,随着y的增加,射流变得越来越薄(图10(a)),液体被不断剪切导致其黏性系数持续下降,在喷嘴出口处液体的黏性系数为0.95,到y/D=3时降至0.80左右。在y/D=3~5之间,由于液体的厚度仅微弱变化,因此黏性系数也基本维持在0.80附近。y/D>5后的黏性系数增加主要是受射流头部较厚、内部黏性系数较高的影响。

图11 t*=9.2时刻液体的黏性分布沿y轴的变化Fig.11 Spatial distribution of viscosity in liquid phase along ydirection at t*=9.2
在图2中可以观察到,y/D=3~5之间的射流破碎最为显著,其实这可以从图11中该处液体的较低黏性系数(比μ0低20%)得到解释,因为黏性系数越低,液体越容易破碎。从定量角度看,低黏性系数代表着较大的当地雷诺数,因而此处的液体更为不稳定。
3.5.2 与牛顿液体射流对比

图12 t*=6.7时刻牛顿射流与非牛顿射流对比Fig.12 Comparison of jet structure from Newtonian and non-Newtonian at t* =6.7
为了更清晰地展示非牛顿射流与牛顿射流的区别,本文也开展了牛顿射流的数值模拟,并进行对比,如图12所示。在t*=6.7时刻,两者的总体射流结构是类似的,但存在几处主要区别:①射流边缘的液体破碎,对非牛顿流体而言,由于边缘处剪切率大,液体的黏性系数低,因此分裂成液丝与液滴,但在牛顿射流中,液体才刚刚出现破裂;②非牛顿射流的头部形成一个液体薄层,而在牛顿射流中并不存在;③二者的展向扩散特性不同。牛顿射流的最宽处为2.9D,而非牛顿射流的最宽处达到3.3D,两者的扩散角相差也超过了20%。因此即使液体只有弱的非牛顿特性,横向气流中的射流特征也会出现显著差别。
4 结 论
1)受横向气流作用,射流喷出后存在弯曲与展向扩散,并呈现bag类型破碎。
2)射流在弯曲过程中迎风面的液体表面趋平,下游液体受剪切作用被逐渐拉成薄层。
3)液体的展向扩散在喷注初期最为显著,后趋于稳定,其扩散角最终恒定在约35°。
4)破碎形成的小液滴最高速与最低速相差4倍,圆形液滴直径范围为D/10~D/15。
5)迎风面的涡量沿液体表面发展,而背风面气流形成复杂尾迹区,近似于圆柱绕流。
6)近喷嘴处的射流液体,其高/低黏性系数相差超过20%,而在破碎区液体的黏性系数最低。
7)与牛顿流体相比,剪切稀化非牛顿射流在头部形成单独的液体薄层且更易破碎,其展向扩散角也更大。
致 谢
本文部分工作是在德国斯图加特大学完成,因此特别感谢Bernhard Weigand教授和Moritz Ertl博士的帮助与讨论,也要感谢斯图加特高性能计算中心对本工作的大力支持。同时,本文作者也要感谢厦门大学校长基金对该课题的资助。
[1] LEE K,AALBURG C,DIEZ F J,et al.Primary breakup of turbulent round liquid jets in uniform crossflows[J].AIAA Journal,2007,45(8):1907-1916.
[2] SALLAM K A,AALBURG C,FAETH G M.Breakup of round nonturbulent liquid jets in gaseous crossflow[J].AIAA Journal,2004,42(12):2529-2540.
[3] BIROUK M, NYANTEKYI-KWAKYE B,POPPLE-WELL N.Effect of nozzle geometry on breakup length and trajectory of liquid jet in subsonic crossflow[J].Atomization and Sprays,2011,21(10):847-865.
[4] WU P,KIRKENDALL K A,FULLER R P.Breakup process of liquid jets in subsonic crossflows[J].Journal of Propulsion and Power,1997,13(1):64-73.
[5] STENZLER J N,LEE J G,SANTAVICCA D A.Penetration of liquid jets in cross-flow[J].Atomization and Sprays,2006,16(8):887-906.
[6] GUTMARK E J,IBRAHIM I M,MURUGAPPAN S.Circular and noncircular subsonic jets in cross flow[J].Physics of Fluids,2008,20(7):075110.
[7] SHAPIRO S R,KING J M,CLOSKEY R T M.Optimization of controlled jets in crossflow[J].AIAA Journal,2006,44(6):1292-1298.
[8] MEGERIAN S,DAVITIAN J,ALVES L S B.Transverse-jet shear-layer instabilities.Part 1.Experimental studies[J].Journal of Fluid Mechanics,2007,593:93-129.
[9] COLETTI F,ELKINS C J,EATON J K.An inclined jet in crossflow under the effect of streamwise pressure gradients[J].Experiments in Fluids,2013,54:1589.
[10] HERRMANN M.Detailed numerical simulations of the primary atomization of a turbulent liquid jet in crossflow[J].Journal of Engineering for Gas Turbine and Power,2010,132(6):061506.
[11] HERRMANN M.The influence of density ratio on the primary atomization of a turbulent liquid jet in crossflow[J].Proceedings of Combustion Institute,2011,33(2):2079-2088.
[12] CAVAR D,MEYER K E.LES of turbulent jet in cross flow:Part 2.POD analysis and identification of coherent structures[J].International Journal of Heat and Fluid Flow,2012,36:35-46.
[13] GALEAZZO F C C,DONNERT G,CARDENAS C,et al.Computational modeling of turbulent mixing in a jet in crossflow[J].International Journal of Heat and Fluid Flow,2013,41:55-65.
[14] SAU R,MAHESH K.Optimization of pulsed jets in crossflow[J].Journal of Fluid Mechanics,2010,653:365-390.
[15] PAI M G,DESJARDINS O,PITSCH H.Detailed simulations of primary breakup of turbulent liquid jets in crossflow[R].Stanford,CA:Center for Turbulence Research,2008:451-466.
[16] MULDOON F,ACHARYA S.Direct numerical simulation of pulsed jets in crossflow[J].Computers & Fluids,2010,39(10):1745-1773.
[17] MARGASON R J.Fifty years of jet in crossflow research:AGARD CP[R].Paris:AGARD,1993,534:1-41.
[18] AALBURG C,VAN LEER B,FAETH G M,et al.Properties of nonturbulent round liquid jets in uniform gaseous cross flows[J].Atomization and Sprays,2005,15(3):271-294.
[19] MAHESH K.The interaction of jets with crossflow[J].Annual Review of Fluid Mechanics,2013,45:379-407.
[20] WONG D C Y,SIMMONS M J H,DECENT S P,et al.Break-up dynamics and drop size distributions created from spiraling liquid jets[J].International Journal of Multiphase Flow,2004,30:499-520.
[21] CLASEN C,EGGERS J,FONTELOS M A,et al.The beads-on-string structure of viscoelastic threads[J].Journal of Fluid Mechanics,2006,556:283-308.
[22] YARIN A L.Free liquid jets and films:Hydrodynamics and rheology[M].New York:Wiley,1993.
[23] HIRT C W,NICHOLS B D.Volume of fluid (VOF)method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39:201-225.
[24] RIDER W J,KOTHE D B.Reconstructing volume tracking[J].Journal of Computational Physics,1998,141:112-152.
[25] KORNEV N,HASSEL E.Synthesis of homogeneous anisotropic divergence free turbulent fields with prescribed second-order statistics by vortex dipoles[J].Physics of Fluids,2007,19(6):068101.
[26] RIDER W J,KOTHE D B.Reconstructing volume tracking[J].Journal of Computational Physics,1998,141:112-152.
[27] GOMAA H,KUMAR S,HUBER C,et al.Numerical comparison of 3Djet breakup using a compression scheme and an interface reconstruction based VOF-code[C]/24th ILASS-Europe,2011.
[28] MOTZIGEMBA M,ROTH N,BOTHE D,et al.The effect of non-Newtonian flow behavior on binary droplet collisions: VOF-simulation and experimental analysis[C]/Proceedings of ILASS-Europe,2002.
[29] FOCKE C,BOTHE D.Computational analysis of binary collisions of shear thinning droplets[J].Journal of Non-Newtonian Fluid Mechanics,2011,166:799-810.
[30] ZHU C,ERTL M,WEIGAND B.Numerical investigation on the primary breakup of an inelastic non-Newtonian liquid jet with inflow turbulence[J].Physics of Fluids,2013,25(8):083102.
[31] SCHROEDER J,LEDERER M L,GAUKEL V,et al.Effect of atomizer geometry and rheological properties on effervescent atomization of aqueous polyvinylphrrolidone solution[C]/24th ILASS-Europe,2011.
[32] YOU Y,LUEDEKE H,HANNEMANN K.On the flow physics of a low momentum flux ratio jet in a supersonicturbulent crossflow[J].Europhysics Letters,2012,97(2):24001.
[33] BATCHELOR G K.The theory of homogeneous turbulence[M].Cambridge:Cambridge University Press,1953.
[34] MUNSON B R,YOUNG D F,OKIISHI T H.Fundamentals of fluid mechanics[M].New York:John Wiley&Sons,2006.
Direct numerical simulation of a non-Newtonian liquid jet in crossflow
ZHU Chengxiang*,YOU Yancheng
School of Aerospace Engineering,Xiamen University,Xiamen 361005,China
A direct numerical simulation study of a non-Newtonian liquid jet in crossflow is carried out with a moderate momentum flux ratio 6.The emphasis of this paper mainly focuses on the flow structure of the jet,including surface behaviors,bending phenomena,spreading features and non-Newtonian characteristics.Deep into the near-field region,it can be observed that the trajectory of the jet oscillates with time and has a tendency to move backward in the reverse direction of the crossflow.The spreading angle increases only at the start of the injection but keeps nearly constant afterwards at 35°.Further insight into the flow physics is obtained by visualizing the primary breakup of the jet,especially the formation of ligaments and droplets,as well as satellite droplets.In the near-field region,the flow feature is similar to that of a circular cylinder,while showing complex turbulent behavior in other regions.The specific non-Newtonian characteristics of the fluid are observed by analyzing the shear thinning viscosity,which varies over 20%spatially inside the liquid.Compared to Newtonian fluids,the current shear thinning non-Newtonian liquid jet shows a stronger breakup feature.
liquid jet;crossflow;non-Newtonian fluid;breakup;direct numerical simulation
2015-09-15;Revised:2015-11-03;Accepted:2016-01-12;Published online:2016-01-31 12:57
URL:www.cnki.net/kcms/detail/11.1929.V.20160131.1257.012.html
s:National Natural Science Foundation of China(91441128;51276151)
V231.2
A
1000-6893(2016)09-2659-10
10.7527/S1000-6893.2016.0004
2015-09-15;退修日期:2015-11-03;录用日期:2016-01-12;网络出版时间:2016-01-31 12:57
www.cnki.net/kcms/detail/11.1929.V.20160131.1257.012.html
国家自然科学基金(91441128;51276151)
*通讯作者.Tel.:0592-2186849 E-mail:chengxiang.zhu@xmu.edu.cn
朱呈祥,尤延铖.横向气流中非牛顿液体射流直接数值模拟[J].航空学报,2016,37(9):26592-668.ZHU C X,YOU Y C.Direct numerical simulation of a non-Newtonian liquid jet in crossflow[J].Acta Aeronautica et Astronautica Sinica,2016,37(9):26592-688.
朱呈祥 男,博士,讲师,硕士生导师。主要研究方向:气液两相流,非牛顿流体力学,气体动力学。Tel:0592-2186849
E-mail:chengxiang.zhu@xmu.edu.cn尤延铖 男,博士,教授,博士生导师。主要研究方向:高超声速流动,计算流体力学。Tel:0592-2186849
E-mail:yancheng.you@xmu.edu.cn
*Corresponding author.Tel.:0592-2186849 E-mail:chengxiang.zhu@xmu.edu.cn
