地基GNSS区域电离层延迟实时格网算法研究
2016-12-05章红平李东俊
王 倩 章红平 黄 玲 李东俊
1 武汉大学GNSS研究中心,武汉市珞喻路129号,430079 2 航天恒星科技有限公司,北京市知春路82号,100089
地基GNSS区域电离层延迟实时格网算法研究
王 倩1章红平1黄 玲1李东俊2
1 武汉大学GNSS研究中心,武汉市珞喻路129号,430079 2 航天恒星科技有限公司,北京市知春路82号,100089
采用中国区域陆态网络跟踪站的GNSS数据,利用载波相位平滑后的组合伪距观测值提取电离层延迟,扣除由CODE产品确定的卫星硬件延迟,利用半变异函数确定VTEC的空间相关性以及由经验值确定的时间相关性,建立VTEC和接收机DCB的随机模型,实现区域电离层实时格网建模。结果表明,模型99.7%的残差分布在1 m以内,内符合精度约0.3 m。以IGS电离层GIM为参考,格网点VTEC周日变化特征与之符合较好。接收机硬件延迟比较稳定,日变化量在1.5 ns以内;利用IGS卫星硬件延迟和球谐系数,从原始观测信息中分离出区域测站接收机硬件延迟,以此为参考,周日均值较差在2 ns以内。
电离层;格网模型;半变异函数;VTEC;DCB
电离层延迟是GNSS 定位的主要误差源。反映全球电离层延迟平均状态的经验模型虽然简单实用,但精度不高[1],改正效果一般在60%左右。对某一时段某一区域内实际测定的电离层延迟,采用数学方法拟合的模型,如三角级数展开模型、二维多项式模型、球谐函数模型和格网模型等[2-6]精度较高。常用的格网模型算法有区域加权平均、三角格网内插、克里金插值等,但在实际应用中各有不足。比如区域加权平均算法不具有分离硬件延迟偏差的能力[5];三角格网内插方法参数过多、计算量较大,且测站、卫星的硬件延迟偏差参数列相关,无法直接分离[7]。由于卫星的硬件延迟在一定时间内变化很小[5],本文使用CODE提供的DCB产品固定卫星硬件延迟,将穿刺点的观测量表示为格网点电离层延迟的线性组合,估计格网点的VTEC和接收机DCB,从而建立区域电离层延迟实时格网模型。
1 模型的建立
1.1 函数模型
为简化,以单层模型代替整个电离层。在该单层球面上,按5°×2.5°的间隔把球面分割成一定数量的网格,在网格区域内的每个穿刺点上,利用双频GNSS 观测值、相位平滑伪距获取电离层延迟,通过数学拟合建立区域电离层延迟模型。
本文使用CODE提供的P2-P1、C1-P2和P1-C1时延偏差产品改正由不同频率观测值(C1、P2)引起的硬件延迟偏差[8]:
STEC=9.524 37(P2-P1)+
9.524 37(b+B)
(1)
式中,(P2-P1)为平滑后的伪距观测值,b和B分别为卫星和接收机的DCB[5]。
将接收机天线到卫星斜路径上的总电子含量STEC转换为天顶方向总电子含量VTEC[2]:
VTEC=STEC/F(z)=STEC·cos(z′)
(2)
式中,z′为穿刺点处的天顶距。
卫星硬件延迟比较稳定[5],每天变化很小,在观测量中可直接扣除卫星的DCB。采用线性内插方法,建立格网点待估参数与观测量之间的观测方程:
(3)
式中,W(di)为加权函数,采用反距离加权法[9]。
假设观测区域有N个格网点、M个测站,以某个历元的穿刺点为例(图1),IPP为穿刺点,Xi为IPP所在格网的节点,d为到节点的距离。
将IPP的VTEC表示为4个节点的函数:
(4)
式中,
其中,xi表示格网点Xi的VTEC,bj表示j测站接收机的DCB,bk表示k卫星的DCB。权重根据穿刺点的高度角来定,即高度角越低,权重越小。

图1 穿刺点与格网点示意图Fig.1 Puncture and grid points diagram
1.2 随机模型
1.2.1 空间过程模型
建立电离层格网模型时,可认为相邻格网点参数波动很小。假设m×n为格网范围,格网点VTEC参数分别为X1,X2,…,Xn,Xn+1,…,Xm+n,空间相关性约束为:
(5)
所有观测量按上述方法形成法方程,并累加到总法方程中。其中虚拟观测方程的方差按照半变异函数计算得到。
1.2.2 时间过程模型
为改善模型时段间的不连续性和不光滑性,在时间域上进行约束,建立时间过程模型。
1)模型初始化。本文计算1周的数据,得到每个测站DCB的日均值。将日均值作为DCB初值再次计算,对1周的接收机DCB日均值取平均得到周日均值,以此作为各个接收机DCB的初值B0。以第i个测站为例:
(6)
2)时间过程描述。在各个时段之间,针对格网点VTEC和接收机DCB随机游走的特性,按照零均值、方差随时间呈线性变换的随机过程特征进行时间相关性约束。方差的变化为:
(7)

(8)
式中,VTECi和Bi-1分别为上个历元估计得到的VTEC和DCB。虚拟观测方程的方差根据全球电离层图GIM发布的格网点差值确定。
将每个历元的所有虚拟观测方程加入函数模型联合形成法方程,按最小二乘法解得各特定参数,从而建立起该时段的区域电离层模型。
2 实验结果与分析
选取2014-11-05~11-11(年积日309~315)中国区域陆态网络97个均匀分布的跟踪站的GNSS 数据,格网大小为2.5°×5°,时间分辨率为30 s,见图2。

图2 测站和格网点分布Fig.2 Stations distribution and grid points
为了客观评价区域电离层模型的精度,利用1周的GNSS观测资料建立该时段每天的区域电离层模型,并根据拟合后的残差计算模型的内符合精度。由年积日309的残差分布(图3)可以看出,残差符合正态分布特征,且99.7%的残差分布在-1~1 m区间内,模型拟合精度较好。计算年积日309~315一周的单天拟合残差的RMS日均值,见表1。除每天地方时14:00左右的RMS较大外,其余时间模型的拟合残差日均值都在0.3 m以内,模型精度较好。

图3 年积日309残差分布直方图Fig.3 Residual distribution histogram in DOY 309

年积日309310311312313314315RMS均值/m0.230.310.230.260.230.280.22
2.1 格网节点VTEC 分析
为了评定模型精度,以GIM为参考,计算格网点VTEC与GIM的差异,并统计格网差值的均值和RMS。图4给出年积日309(2014年)UTC 08:00、12:00、16:00和18:00的格网点VTEC相对于CODE的比值,以分析1 d中不同时刻格网点VTEC与GIM差值的相对偏差[10]。

图4 格网点VTEC相对CODE的相对偏差Fig.4 Deviation of grid VTEC to CODE
可以看出,相对偏差最大在40%左右,白天大于晚上,正午时刻最大,这是因为正午太阳活动剧烈、电离层变化大。而GIM是全球整体模型,其标称精度为2~8 TECu,且中国区域测站较少,无法精确描述中国区域的局部、瞬时电离层变化。同时,本文利用随机过程,充分考虑格网点参数的时空变化,可以更准确地体现局部电离层的细节,导致两者在正午偏差较大。另外,由于低纬度地区电离层变化较中高纬地区大,因此低纬度地区格网点VTEC相对偏差明显大于高纬度地区。
图5给出UTC12:00的穿刺点分布图,格网区域的边缘穿刺点较为稀疏,而内部的穿刺点多,观测信息丰富。这与格网点VTEC的精度边缘化相似。所以,格网点的精度可能和穿刺点的密集稀疏程度有关,VTEC差值大的格网点是由于缺少数据、观测不充分引起的。

图5 穿刺点分布图(UTC12:00)Fig.5 Puncture points distribution(UTC12:00)
2.2 接收机硬件延迟偏差DCB 分析
各个测站接收机1周的DCB日均值标准差可以反映DCB的内符合精度,如图6所示,五角星对应的测站位于格网边缘(下同)。可以看出,标准差大于1 ns的测站都位于格网边缘,其余测站均在1 ns以内。这是由于格网边缘的测站对应的穿刺点少,观测信息不充分,导致接收机DCB误差较大。

图6 DCB周日均值标准差图Fig.6 Daily average standard deviation chart
为评估DCB的外符合精度,利用IGS卫星硬件延迟和球谐系数,从原始观测信息分离出区域测站接收机的硬件延迟,比较与之单天日均值较差(图7)。结果表明,日均值较差大于1.5 ns的测站共有16个,均分布于格网边缘,说明格网内部精度优于边缘表现在格网点VTEC和接收机DCB两个方面。
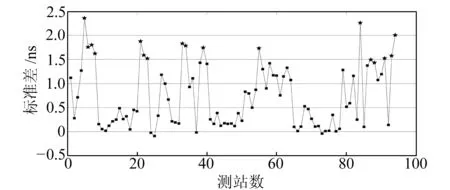
图7 接收机DCB周日均值较差Fig.7 Daily deviation of receiver DCB
3 结 语
本文利用相位平滑伪距提取电离层延迟,根据穿刺点和格网点空间距离的相关性,采用线性内插方法构建电离层延迟的时间和空间随机过程模型,实现区域电离层实时格网建模。结果表明:1)模型拟合残差3倍误差99.7%都在1 m以内,精度较好;2)格网点VTEC与CODE周日变化符合较好,低纬度地区和正午的电离层TEC波动大,精度较差,源于电离层正午活动剧烈、噪声大,随机模型难以准确描述,接收机DCB日变化很小,大部分在1 ns以内,比较稳定;3)格网点VTEC和接收机DCB都存在边际效应,对应的格网点VTEC和接收机DCB精度低于区域内部。若选择区域分布更均匀的测站观测值,有望进一步提高模型精度。
[1] 张小红,李征航, 张建军. 利用GPS观测值建立区域性VTEC电离层模型研究[C].中国全球定位系统技术应用协会年会,宁波,1999 (Zhang Xiaohong, Li Zhenghang, Zhang Jianjun. Research for Regional VTEC Ionospheric Models by Using GPS Observation[C].Annual Meeting of China Technical Application Association for Global Positioning System,Ningbo,1999)
[2] 章红平.基于地基GPS 的中国区域电离层监测与延迟改正研究[D].北京: 中国科学院研究生院,2006(Zhang Hongping, Regional Ionospheric Monitoring and Delay Correction Based on the Ground-Based GPS in China[D]. Beijing: Graduate University of the Chinese Academy of Sciences,2006)
[3] 袁运斌.基于GPS 的电离层监测及延迟改正理论与方法的研究[D].北京: 中国科学院研究生院,2002(Yuan Yunbin. Theory and Method of Regional Ionospheric Monitoring and Delay Correction Based on the GPS[D]. Beijing: Graduate University of the Chinese Academy of Sciences, 2002)
[4] 刘经南,陈俊勇,张燕平,等.广域差分GPS 原理与方法[M].北京: 测绘出版社,1999(Liu Jingnan, Chen Junyong, Zhang Yan, et al. Wide-Area Differential GPS Principle and Method[M].Beijing: Surveying and Mapping Press, 1999)
[5] 耿长江. 利用地基GNSS数据实时监测电离层延迟理论与方法研究[D].武汉:武汉大学,2011(Geng Changjiang. Theory and Method of Ionospheric Real-Time Monitoring and Delay Correction Based on the Ground-based GNSS[D]. Wuhan:Wuhan University,2011)
[6] 章红平,施闯,唐卫明.地基GPS区域电离层多项式模型与硬件延迟统一解算分析[J].武汉大学学报:信息科学版,2008,33(8):805-809(Zhang Hongping, Shi Chuang, Tang Weiming. Unified Calculation and Analysis of Ground-Based GPS Regional Ionospheric Polynomial Model and the Hardware Delay[J].Geomatics and Information Science of Wuhan University, 2008,33(8):805-809)
[7] 章红平,韩文慧,黄玲等.地基GNSS全球电离层延迟建模[J]. 武汉大学学报:信息科学版,2012,37(10):1 186-1 189(Zhang Hongping,Han Wenhui, Huang Ling,et al. Modeling Global Ionospheric Delay with IGS Ground-Based GNSS Observations[J].Geomatics and Information Science of Wuhan University, 2012,37(10):1 186-1 189)
[8] 李征航,黄劲松. GPS测量与数据处理[M]. 武汉:武汉大学出版社,2009(Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing [M].Wuhan: Wuhan University Press,2009)
[9] 余小东,武莹,何腊梅.反距离加权网格化插值算法的改进及比较[J]. 工程地球物理学报,2013, 10(6):900-904(Yu Xiaodong, Wu Ying, He Lamei. Imporvement and Comparison of Inverse Distance Weighted Grid Interpolation Algorithm[J]. Chinese Journal of Engineering Geophysics,2013,10(6):900-904)
[10]Mannucci A J, Wilson B D, Yuan D N, et al. A Global Mapping Technique for GPS-Derived Ionospheric Total Electron Content Measurements[J]. Radio Science, 1998, 33(3):565-582
About the first author:WANG Qian, postgraduate, majors in ionosphere modeling and RTK, E-mail:qwangwhu@163.com.
Real-Time Grid Algorithm Study of Ground-Based GNSS Regional Ionospheric Delay
WANGQian1ZHANGHongping1HUANGLing1LIDongjun2
1 GNSS Research Center,Wuhan University,129 Luoyu Road, Wuhan 430079,China 2 Space Star Technology Co Ltd,82 Zhichun Road, Beijing 100089,China
Based on GNSS data from the crustal movement observation network of China (CMONOC), we extract ionospheric delay from levelled carrier-phase observations, deduct the satellite hardware delay, then attach stochastic models of VTEC and DCB; these apply the semi-variable function as the spatial constraint of VTEC and the experienced VTEC and receiver hardware delay as the periods constraint, thus setting up the regional ionospheric grid model in real time. The results show that the inner precision of the model is about 0.3 m and the residuals are within 1 m. Taking GIM, which is the IGS ionospheric delay product, as reference, the characteristics of sequence diagram of VTEC are in accordance with GIM for a week. Furthermore, receiver hardware delay, with variations within 1.5 ns each day, are relatively stable. Compared with the regional station receiver hardware delay isolated from the original observation by using satellite hardware delay and spherical harmonic coefficient of IGS, the mean differences for a week are all within 2 ns.
ionosphere; grid model; semivariable function; VTEC; DCB
National Natural Science Foundation of China, No.41231064; National High Technology Research and Development Program of China, No.2014AA123101.
2015-12-16
项目来源:国家自然科学基金(41231064);国家863计划(2014AA123101)。
王倩,硕士生,主要研究方向为电离层建模和相对定位,E-mail:qwangwhu@163.com。
10.14075/j.jgg.2016.12.008
1671-5942(2016)012-1069-04
P228
A
