一种顾及钟差周期误差和随机特性的卫星钟差预报方法

孙大双 吕志平 王宇谱 李柏地 王 宁

1 信息工程大学地理空间信息学院，郑州市科学大道62号，450001 2 解放军78092部队,成都市，610000



一种顾及钟差周期误差和随机特性的卫星钟差预报方法

孙大双1吕志平1王宇谱1李柏地2王 宁1

1 信息工程大学地理空间信息学院，郑州市科学大道62号，450001 2 解放军78092部队,成都市，610000

提出一种顾及钟差周期误差和随机特性的卫星钟差预报方法。首先通过比较二次多项式加1、2、3、4个主要周期误差的模型，取其优者求得钟差预报的拟合值;然后针对拟合残差值的随机特性采用灰色模型进行建模，求得拟合值残差预报值；最后，将其与之前求得的预报值相结合得到最终的钟差预报值。采用IGS的15 min精密钟差数据进行实验，结果表明，在短期预报中，加2个主要周期误差的模型预报性能最好，并且新模型的预报精度优于常用算法。

二次多项式模型；灰色模型；周期误差；卫星钟差；随机特性

目前，IGS提供的精密钟差产品精度约0.1 ns，但实时性较差；而广播星历和快速钟差预报产品的精度不高，无法满足高精度定位的要求[1-2]。研究表明，原子钟的频率总波动是多种不同噪声的线性组合[3-5]，因此建立精确的原子钟运行模型非常困难。很多学者构造了不同的模型以及各种组合模型进行钟差预报研究[1,6-10]。其中，二次多项式模型(QP模型)和灰色模型(GM模型)是最常用的预报模型，但这两种方法都仅仅研究了钟差趋势项函数模型。虽然考虑周期误差的二次多项式模型预报效果较好，但没有考虑随机项对钟差预报的影响。

本文基于二次多项式模型和灰色模型，提出一种顾及钟差周期误差和随机特性的卫星钟差预报方法。首先比较4种二次多项式加不同主要周期误差的模型，取其优者求得钟差预报的拟合值；然后针对拟合残差值的随机特性采用灰色模型进行建模，求得拟合值残差预报值；最后将其与二次多项式加主要周期误差模型求得的钟差预报值相结合，得到最终的钟差预报值。利用IGS官方网站的15 min精密钟差数据进行短期钟差预报，比较不同算法的预报精度并得出相应结论。

1 原 理

钟差预报的二次多项式模型误差方程为[11]：

(1)

式中，Li为历元时刻ti的卫星钟差，a0、a1、a2分别为参考时刻t0的卫星钟差、钟速和卫星钟的频漂，Δi为模型残差。根据最小二乘原理，当钟差数据多于3个时，可解算得到未知参数的最或然值。

在钟差拟合预报中，除考虑钟差的趋势项，还应考虑其周期变化特性。附加周期误差的二次多项式模型为：

(2)

式中，p为周期误差个数，Ak、fk、φk分别为对应周期误差的振幅、频率和相位。

由文献[12]可知，星载原子钟受周期误差影响的顺序由大到小为12 h、6 h、4 h、3 h，也有学者认为取前两个周期误差即可[12-13]，即p=4或2。通过二次多项式加周期误差的模型[13]所得到的拟合残差值会受到各种噪声组合的随机项以及模型本身不足等因素的影响，而各种噪声的组合情况变化无常，很难得到其细致的变化规律。以2012-10-01精密钟差数据中PRN32卫星的数据进行二次多项式加两个主要周期误差建模为例，求得2012-10-02的钟差预报残差值(图1)。

图1 PRN32卫星钟差预报残差Fig.1 The error of clock bias prediction of satellite PRN32

由图1可知，预报残差值的大小受到预报模型或原子钟本身及各种因素的影响而无法获得其细致的变化规律，大致呈现出递增或递减的趋势，符合灰色系统建模的基本条件[6,14-16]。通过对原始数据进行累加或累减生成一组规律性较强的新序列，对新序列可以建立灰色模型。

基于此，本文提出一种顾及钟差周期误差和随机特性的卫星钟差预报方法，其模型表达式为:

(3)

式中，GM(1,1)表示灰色模型，其微分方程表达式为dx/dt+ax=u。a、u分别为发展系数和灰色作用量，x为数据序列，t为时间。

由于GM(1,1)模型要求计算序列是非负的[17]，在对二次多项式加主要周期误差模型得到的拟合残差值进行灰色建模时，必须检查残差值序列的正负号是否一致。若不是，则给每一个残差值都加上一个常数c，从而使该序列的符号一致。由此得到的序列预报值再减去常数c，即可得到残差值的预报值[18]。如图1所示，预报残差值序列有正有负，应当对其进行处理。对于常数c的具体取值，目前已有文献没有明确说明。本文通过对比加上不同大小的常数c的钟差预报实验发现，在预报过程中，常数c越大，精度越高；达到一定程度后，精度不再提高。其原因是，当所加常数c达到某一数值后，正数序列的特性趋于稳定，其数值不再对模型预报结果产生较明显的影响。

该组合预报方法的基本思路为：使用初始钟差数据L(0)={l(0)(i),i=1,2,…,n}进行二次多项式加主要周期误差建模；将L减去二次多项式加主要周期误差求得的拟合钟差值L1，得到拟合钟差值的误差V1；对所得的拟合误差V1采用基于最小二乘的GM(1,1)模型进行建模，并得到拟合误差的预报值V2；最后，将V2加上由二次多项式加主要周期误差模型的钟差预报值P1，得到最终的钟差预报值P。为了验证主要周期误差个数对卫星钟差短期预报效果的影响，本文采用4种组合方式：1)考虑12 h一个周期误差；2)考虑12 h和6 h两个周期误差；3)考虑12 h、6 h和3 h三个周期误差；4)考虑12 h、6 h、4 h和3 h四个周期误差，分别进行钟差预报，取其优者的拟合误差值进行灰色建模，如图2所示。

图2 组合钟差预报模型解算流程Fig.2 Calculating process of combination model for clock bias prediction

定义钟差预报的均方根误差为：

(4)

式中，εi为i时刻钟差预报误差，Pi为i时刻钟差预报值，Li为i时刻IGS精密钟差值。

2 算例分析

本文采用GPS系统15 min采样间隔的最终精密钟差产品进行预报实验，从IGS官方网站下载2012-09-29～2013-09-28的精密钟差数据。目前的星载原子钟有BLOCK ⅡA型、BLOCK ⅡR型、BLOCK ⅡR-M型、BLOCK ⅡF型4种(表1)。

超快速(IGU)产品虽然既含实测数据又有预报数据，但其数据质量却相对较差，存在起点偏差、数据粗差及钟跳相对严重等问题。因此，在钟差预报实验中，本文选取该时间段内未出现钟差跳变和间断的完整钟差数据进行相关研究，且以其为参考真值，计算每次预报结果的均方根误差。为了避免某一天的预报精度较好或较差而对模型的预报性能造成影响，选取每颗星钟差预报多次的均方根误差的均值(mean)、最小值(min)以及极差值(range)作为统计量，并统计这3个量的平均值，以此来分析各种卫星钟差预报模型在连续钟差预报中的效果。

表1 GPS系统搭载原子钟的在轨卫星(截止到2014-07-14)

下文字母意义如下：QPT1表示二次多项式加1个主要周期误差(12 h)模型，QPT2表示二次多项式加2个主要周期误差(12 h、6 h)模型，QPT3表示二次多项式加3个主要周期误差(12 h、6 h、4 h)模型，QPT4表示二次多项式加4个主要周期误差(12 h、6 h、4 h、3 h)模型，QPGM表示二次多项式模型与灰色模型结合的组合模型，QPT2GM表示二次多项式加2个主要周期误差(12 h、6 h)模型与灰色模型相结合的组合模型。

设计两个算例对各模型的钟差预报效果进行分析。

算例1 选择2013-06-16～07-29以4 d为窗口、每次向前滑动1 d的钟差数据，采用QPT1模型、QPT2模型、QPT3模型和QPT4模型分别连续进行40次的6 h、12 h和24 h钟差预报。为比较4种模型的预报性能，统计4种模型连续40次预报结果的均方根误差最小值、平均值和极差值，其平均值见表2。

表2 算例1中各项统计量平均值

由各颗卫星的预报结果可知，所有卫星钟差预报均方根误差平均值都在ns级甚至亚ns级，说明4种模型均有良好的预报性能。同时，相比于其他卫星，PRN04、PRN08、PRN10、PRN24、PRN28连续40次钟差预报的均方根误差平均值和极差值较大，说明采用这4种模型进行钟差预报时，搭载Rb原子钟的卫星钟差预报性能优于搭载Cs原子钟的卫星，后期发射的卫星钟差预报性能优于早期发射的卫星。分别对比4种模型对不同卫星预报不同长度钟差的均方根误差平均值和极差值可知，4种模型的预报精度随着预报时间的增加逐渐降低。

由表2可知，后3种模型的预报性能优于QPT1模型，与QPT1模型的min、mean和range平均值之差分别在10-11、10-12、10-11量级。 QPT2模型的range平均值大于其他几种模型，其原因是QPT2模型的min平均值优于另外3种模型，若数据质量下降，QPT2模型的RMS值与另外3种模型相当时，则会出现QPT2模型的range平均值偏大的情况。再者，QPT2模型的mean平均值明显优于另外3种模型，因此，由min、mean、range 3统计量的平均值综合分析可得，QPT2模型的钟差预报性能是4种模型中最好的。

算例2 由算例1可知，QPT2模型的预报性能在4种模型中是最优的。选取2012-09-29～11-11以4 d为窗口、每次向前滑动1 d的钟差数据，采用QP、QPT2、QPT2GM、QPGM和GM模型分别连续进行40次6 h、12 h和24 h钟差预报。在QPT2GM和QPGM模型中，采用QPT2和QP模型拟合残差值中最后48个历元进行灰色建模，将连续40次6 h预报结果的均方根误差平均值和极差值绘制成图(图3、图4)。由于篇幅所限，将所有卫星预报时长为6 h、24 h的结果统计量平均值统计在表3中。

由图3、图4可知，5种模型进行6 h钟差预报的结果精度均在ns级和亚ns级(大部分在亚ns级)，说明5种模型的预报结果都比较可靠。QPT2GM模型的预报精度及稳定性优于其余4种模型，说明对少量QPT2模型的拟合残差值进行灰色建模可以提高预报残差值的可靠性。

由表3可知，相比于其他4种模型，QPT2GM模型解得的各项统计量平均值都较小，表明QPT2GM模型的钟差预报精度与稳定性优于其余4种模型。同时，对比两种原子钟的预报效果可知，采用文中几种方法进行钟差预报时，Rb钟的预报效果优于Cs钟，其连续40次预报均方根误差的min及mean的平均值比Cs钟小80%以上，其连续40次预报均方根误差range的平均值比Cs钟小70%以上。QPT2GM模型对Cs钟的改善尤为明显，提高的效率是Rb钟的2倍以上。

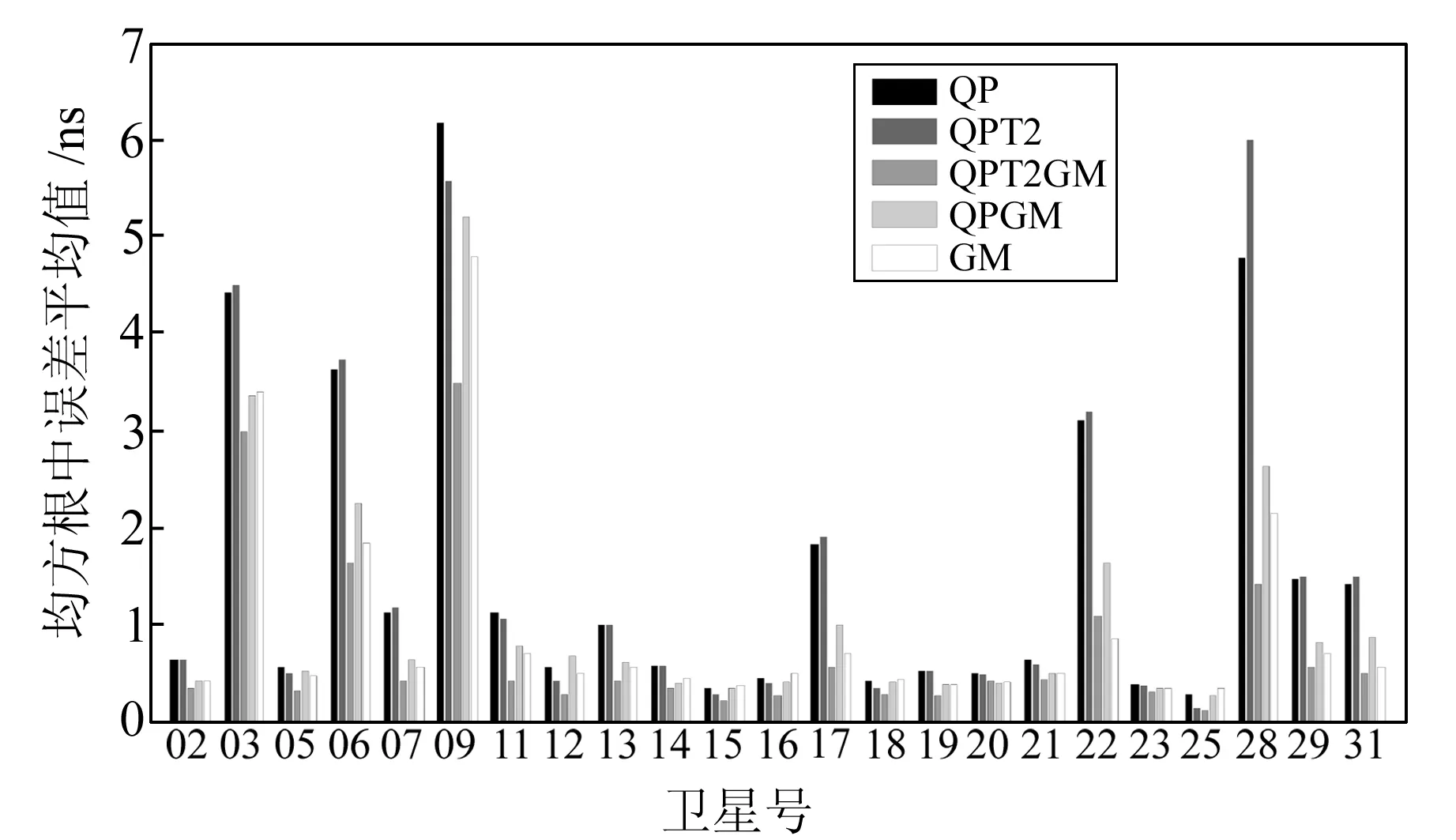
图3 不同模型4 d数据预报6 h钟差RMS平均值Fig.3 The mean value of RMS of four days clock’s prediction in 6 h with different models

图4 不同模型4 d数据预报6 h钟差RMS极差值Fig.4 The range value of RMS of four days clock’s prediction in 6 h with different models

各统计量平均值原子钟预报6h/ns预报24h/nsQPQPT2QPT2GMQPGMGMQPQPT2QPT2GMQPGMGMminRb0.2280.1980.1360.1940.1860.3820.3400.2560.3190.312Cs1.3490.9740.8711.1351.2213.0502.1521.6471.8082.319meanRb1.2131.2130.5220.7840.6632.3972.3791.4971.6501.522Cs5.3125.0563.2374.2714.1238.7358.4547.0307.6146.668rangeRb4.2524.4081.5082.3031.9737.7537.8025.5485.7555.967Cs12.05811.5205.9979.0509.36823.95224.84418.34218.46016.848

3 结 语

1)本文所提算法的解算精度及稳定性在卫星钟差短期预报中均优于常用算法，可以作为一种较好的钟差预报模型，且采用该模型进行卫星钟差预报时，Rb钟的预报效果优于Cs钟。

2)在一定精度范围内，进行卫星钟差短期预报时可以只考虑2个主要周期误差。

3)钟差预报模型的预报性能与星载原子钟的类型及发射时间有关，后期发射的卫星钟差预报性能优于早期卫星，与目前已公开的结论一致。

4)本文对钟差趋势项进行建模时采用二次多项式模型，但是该模型并不适用于所有类型的卫星，在以后工作中将对其作进一步研究。

[1] 王宇谱，吕志平，陈正生，等.卫星钟差预报的小波神经网络算法研究[J].测绘学报，2013，42(3)：323-330(Wang Yupu, Lü Zhiping, Chen Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 323-330)

[2] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2014(Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M].Wuhan: Wuhan University Press, 2014)

[3] Galleani L, Sacerdote L, Tavella P, et al. A Mathematical Model for the Atomic Clock Error[J]. Metrologia, 2003,40(3):257-264

[4] Allan D W. Time and Frequency (Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1987,34(6):647-654

[5] 郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州：信息工程大学，2006(Guo Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou:Information Engineering University,2006)

[6] 崔先强，焦文海. 灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报：信息科学版，2005，30(5)：447-450(Cui Xianqiang, Jiao Wenhai. Gray System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University,2005,30(5):447-450)

[7] 黄观文，杨元喜，张勤.开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报[J].测绘学报，2011，40(1):15-21(Huang Guanwen, Yang Yuanxi, Zhang Qin. Estimate and Predict Satellite Clock Error Using Adaptively Factors Based on Opening Windows[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 15-21)

[8] 王宇谱，吕志平，崔阳，等.利用遗传小波神经网络预报导航卫星钟差[J]. 武汉大学学报：信息科学版，2014，39(7)：809-814(Wang Yupu, Lü Zhiping, Cui Yang, et al. Predicting Navigation Satellite Clock Bias Using a Genetic Wavelet Neural Network[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7):809-814)

[9] Hu Y, Tang D P. Application of a Novel Data Mining Method Based on Wavelet Analysis and Chaotic Neural Network on Satellite Clock Bias Prediction[J]. Applied Mechanics and Materials, 2014, 513-517:1 144-1 149

[10]Yuan H B, Wang Z M, Dong S W, et al. Dynamic Grey-Autoregressive Model of an Atomic Clock[J].Metrologia, 2008,45(6):S1-S5

[11]郑作亚，陈永奇，卢秀山.灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J].天文学报，2008，49(3)：306-320(Zheng Zuoya, Chen Yongqi, Lu Xiushan. An Improved Grey Model for the Prediction of Real-time GPS Satellite Clock Bias[J]. Acta Astronomica Sincia,2008,49(3):306-320)

[12]John D, Santosh B, Marek Z. Development of a Kalman Filter Based GPS Satellite Clock Time-offset Prediction Algorithm[C]. European Frequency and Time Forum(EFTF), 2012

[13]Kenneth L S, Jim R R, Ronald L B. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions,2008, 12(3):211-225

[14]郑作亚，党亚民，卢秀山，等.附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J].天文学报，2010，51(1)：95-102(Zheng Zuoya, Dang Yamin, Lu Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sincia,2010,51(1):95-102)

[15]Zhao C S. Grey System Theory and Its Applications[J]. Journal of Grey System, 2015,27(1):127-129

[16]路晓峰，杨志强，贾晓林，等.灰色系统理论的优化方法及其在卫星钟差预报中的应用[J].武汉大学学报：信息科学版，2008，33(5)：492-495(Lu Xiaofeng, Yang Zhiqiang, Jia Xiaolin, et al. Parameter Optimization Method of Gray System Theory for the Satellite Clock Error Predicating[J]. Geomatics and Information Science of Wuhan University, 2008,33(5):492-495)

[17]尹逊震.灰色模型的改进及其应用[D].南京：南京信息工程大学,2008(Yin Xunzhen. The Improved Grey Model and Its Applications[D].Nanjing: Nanjing University of Information Science & Technology,2008)

[18]李玮，程鹏飞，秘金钟.灰色模型在快速卫星钟差预报中的应用[J].测绘科学，2010，35(3)：43-45(Li Wei, Cheng Pengfei, Bei Jinzhong. Grey System Model for the Ultra-rapid Satellite Clock Error Predicting[J]. Science of Surveying and Mapping, 2010,35(3):43-45)

About the first author:SUN Dashuang, postgraduate, majors in theory and method of surveying data processing, E-mail:sundashuang1992@163.com.

A Method of Satellite Clock Bias Prediction Considering Periodic Errors and Stochastic Characteristics

SUNDashuang1LÜZhiping1WANGYupu1LIBodi2WANGNing1

1 School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China 2 78092 Troops，Chengdu 610000,China

In order to improve satellite clock bias prediction, a new prediction method is proposed considering periodic errors and stochastic characteristics. First, the given satellite clock bias is fitted by four quadratic polynomial models with one to four dominating periodic errors; the best model is then chosen to obtain the fitting residuals. Then, the prediction of the fitting residuals is modeled based on grey model, considering the stochastic characteristics of the fitting residuals. Finally, the clock bias based on the best of the four models and prediction of the fitting residuals are combined to obtain the ultimate prediction result. The precise data of satellite clock bias within 15 min from IGS are used to conduct experiments on different models. The results show that the model with two dominating periodic errors is better than the model with other dominating periodic errors and that the proposed model performs better than commonly used models in short-term prediction.

quadratic polynomial model; grey model; periodic error; satellite clock bias; stochastic characteristic

National Natural Science Foundation of China, No.41274015; National Key Research and Development Program of China, No.2016YFB0501701; Open Fund of State Key Laboratory of Geo-Information Engineering, No.SKLGIE2015-M-2-1.

2015-11-02

项目来源：国家自然科学基金(41274015);国家重点研发计划(2016YFB0501701)；地理信息工程国家重点实验室开放基金(SKLGIE2015-M-2-1)。

孙大双，硕士生，主要从事测量数据处理方法与理论研究，E-mail：sundashuang1992@163.com。

10.14075/j.jgg.2016.12.010

1671-5942(2016)012-1078-05

P228

A