基于修正钟差一次差分数据的卫星钟差预报

王宇谱 吕志平 周海涛 王 宁 翟树峰

1 信息工程大学地理空间信息学院，郑州市科学大道62号，450001 2 地理信息工程国家重点实验室，西安市雁塔路中段1号，710054



基于修正钟差一次差分数据的卫星钟差预报

王宇谱1,2吕志平1周海涛1王 宁1翟树峰1

1 信息工程大学地理空间信息学院，郑州市科学大道62号，450001 2 地理信息工程国家重点实验室，西安市雁塔路中段1号，710054

对钟差一次差分预报原理进行改进，分析常用的一次多项式模型、二次多项式模型和灰色模型在采用改进原理进行预报时的相关特性。结果表明，对钟差一次差分预报原理的改进是有效的，可以提高常用模型在钟差短期预报中的预报精度。

导航卫星；钟差预报；一次差分；数据建模

卫星导航系统中星载原子钟的钟差预报在维持系统的时间同步、优化导航电文中的钟差参数等方面具有重要作用[1]。针对卫星钟差预报，国内外学者建立了大量模型[2-11]。已有的钟差预报研究主要在于模型本身，本文则通过对钟差数据进行一次差分实现钟差建模数据与建模策略的改变，研究基于钟差一次差分数据的卫星钟差预报方法来提高钟差预报的精度。在给出基于钟差一次差分数据的预报原理及其预处理方法的基础上，对钟差一次差分预报原理进行改进，同时分析一次多项式(LP)模型、二次多项式(QP)模型和GM(1,1)模型在采用本文原理进行预报时的相关特性。

1 算法原理

为了记录高精度的时间信息，卫星钟差数据的有效位数通常比较多，数值相对较大，使得钟差数据中的异常数据点容易被掩盖。而相邻历元间的钟差数据其数值变化不大，通过历元间钟差数据的一次差分可以在一定程度上消除原钟差序列趋势项的影响，得到一组有效数字位数减少、便于进行预处理的数据序列。以GPS系统PRN01卫星2015-04-02～04-03的15 min采样间隔的精密钟差数据为例，图1给出其钟差数据，图2是其对应的一次差分数据。

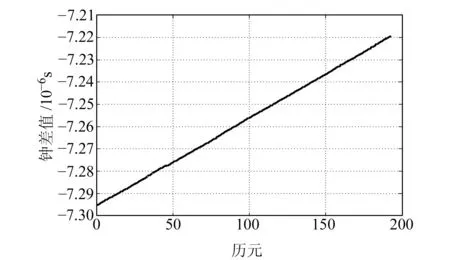
图1 PRN01卫星的钟差数据Fig.1 SCB data of satellite PRN01

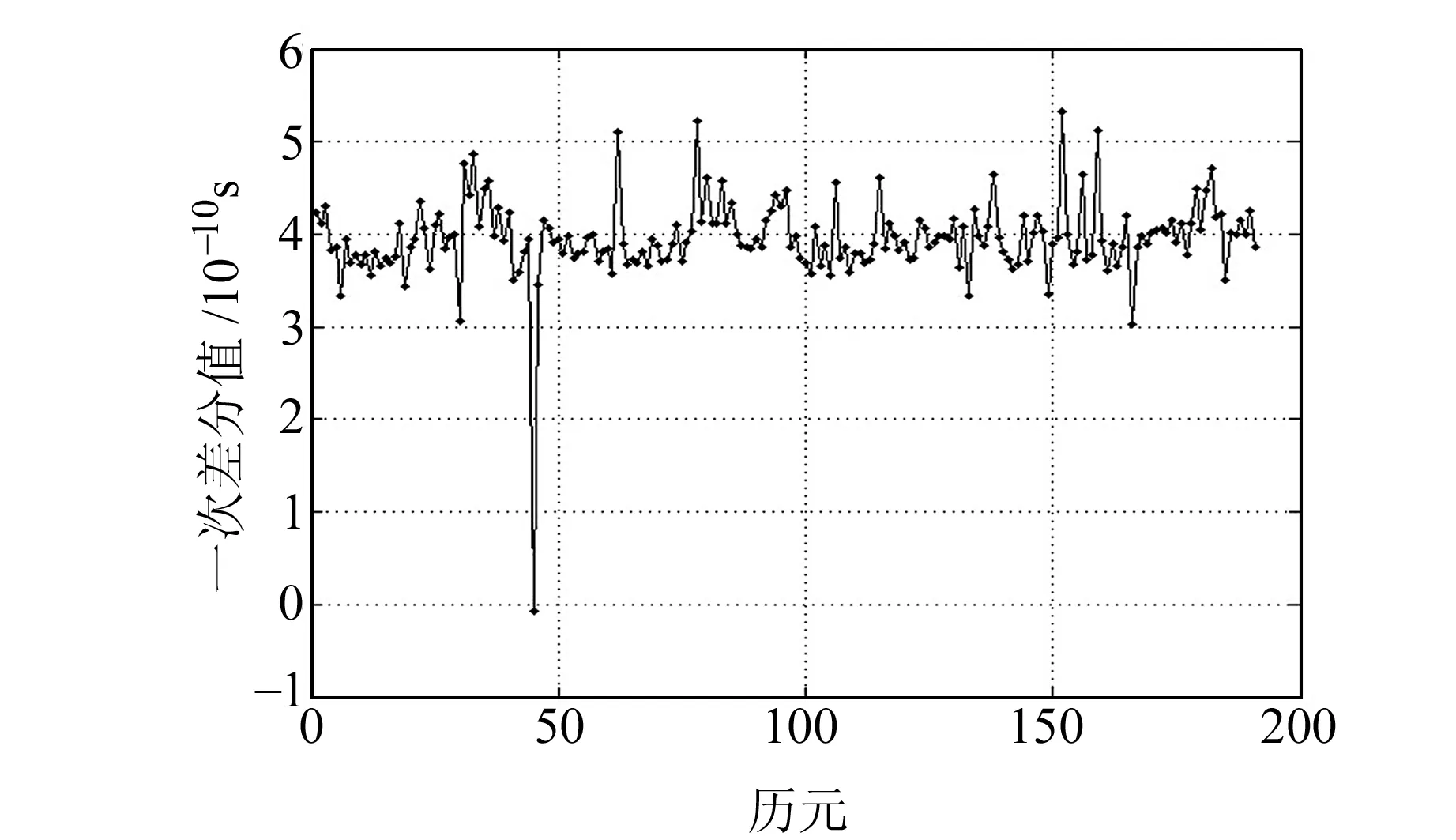
图2 PRN01卫星的钟差一次差分数据Fig.2 Single difference data of SCB of satellite PRN01

对比图1和图2可以看出，原始钟差数据容易掩盖异常数据点，而异常数据点在其对应的一次差分数据中表现为峰值点，从而使得异常值的探测变得相对容易。同时，经过相邻历元间钟差数据的一次差分处理，可以消除原钟差序列中可能存在的系统误差。所以，基于钟差一次差分数据进行钟差拟合预报，既便于数据的预处理，也有利于更加准确地进行数据拟合。

1.1 基于钟差一次差分数据的预报原理[1,8-9]

基于钟差一次差分数据的预报是采用一次差分后的数据序列ΔL来对模型进行平差解算。模型确定之后，预报n-1个一次差分建模数据对应历元以后的m(m>1)个历元的一次差分序列ΔL1={Δl(j),j=n,n+1, …,n+m-1}。然后将一次差分预报序列ΔL1和建模钟差数据的最后一个钟差值l(n)对应相加，从而求得所需预报历元j时刻的钟差值l(j)：

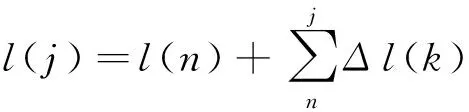
(1)

1.2 基于钟差一次差分数据的预处理方法

针对钟差一次差分数据，文献[7]设计了一种基于改进中位数的异常值探测方法：将每个钟差一次差分数据Δl(i)跟一次差分序列的中数(MED)k及中位数(MAD)数倍之和进行比较。若钟差一次差值:

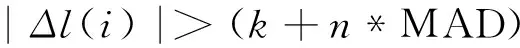
(2)

则认为该一次差分数据是异常值，予以剔除，同时用内插的方法补充该点数据。本文采用三次分段样条方法对剔除历元所对应的钟差一次差值进行内插补充。式(2)中，k= Median{Δl(i)}，MAD=Median{|Δl(i)-k|/0.674 5}，n的取值根据需要确定(本文取n=3)。图3是对应于图2的钟差一次差分数据预处理后的数据，图4为钟差一次差分数据预处理后对应的钟差数据。从图3可看出，通过对异常数据点的处理可以得到质量更好的钟差一次差分数据。

图3 PRN01卫星预处理后的钟差一次差分数据Fig.3 The preprocessed single difference of satellite PRN01

图4 PRN01卫星预处理后的钟差数据Fig.4 The preprocessed SCB data of satellite PRN01

1.3 基于钟差一次差分数据预报原理的改进

从式(1)可以看出，基于钟差一次差分数据的预报，对于建模钟差数据中最后一个数据l(n)的依赖程度高，该数据的可靠性与基于该预报原理的预报结果密切相关。然而，目前基于钟差一次差分预报原理的钟差预报应用中[1,8-9]，没有考虑该问题。

借鉴文献[11]对预报模型的起点偏差修正所采取的策略，本文在钟差一次差分预报原理的基础上，通过采用建模数据中最后5个数据拟合最后1个数据的方式来提高式(1)中l(n)的可靠性，进一步完善钟差一次差分预报原理。其中，所采用的拟合公式是钟差的二次多项式模型，该模型包含了描述钟差所需的相对于卫星导航系统时间的偏差、钟速和钟漂3种确定性参数。为了验证所作改进的有效性，以GPS系统PRN01卫星的钟差预报为例，使用2015-04-06的卫星钟差数据进行建模，预报2015-04-07前6 h的钟差，分析在给已知建模钟差数据最后一个值分别加入0.1 ns、0.5 ns、1.0 ns和2.0 ns的模拟粗差时，基于钟差一次差分预报原理改进前后的预报效果。图5～8是PRN01卫星钟差在不同模拟粗差条件下的预报误差，基于钟差一次差分预报原理的QP模型记为DQP模型，基于改进钟差一次差分预报原理的QP模型记作MDQP模型。表1给出了4种粗差条件下两种模型预报结果的均方根误差(RMS，其定义参见式(3))。

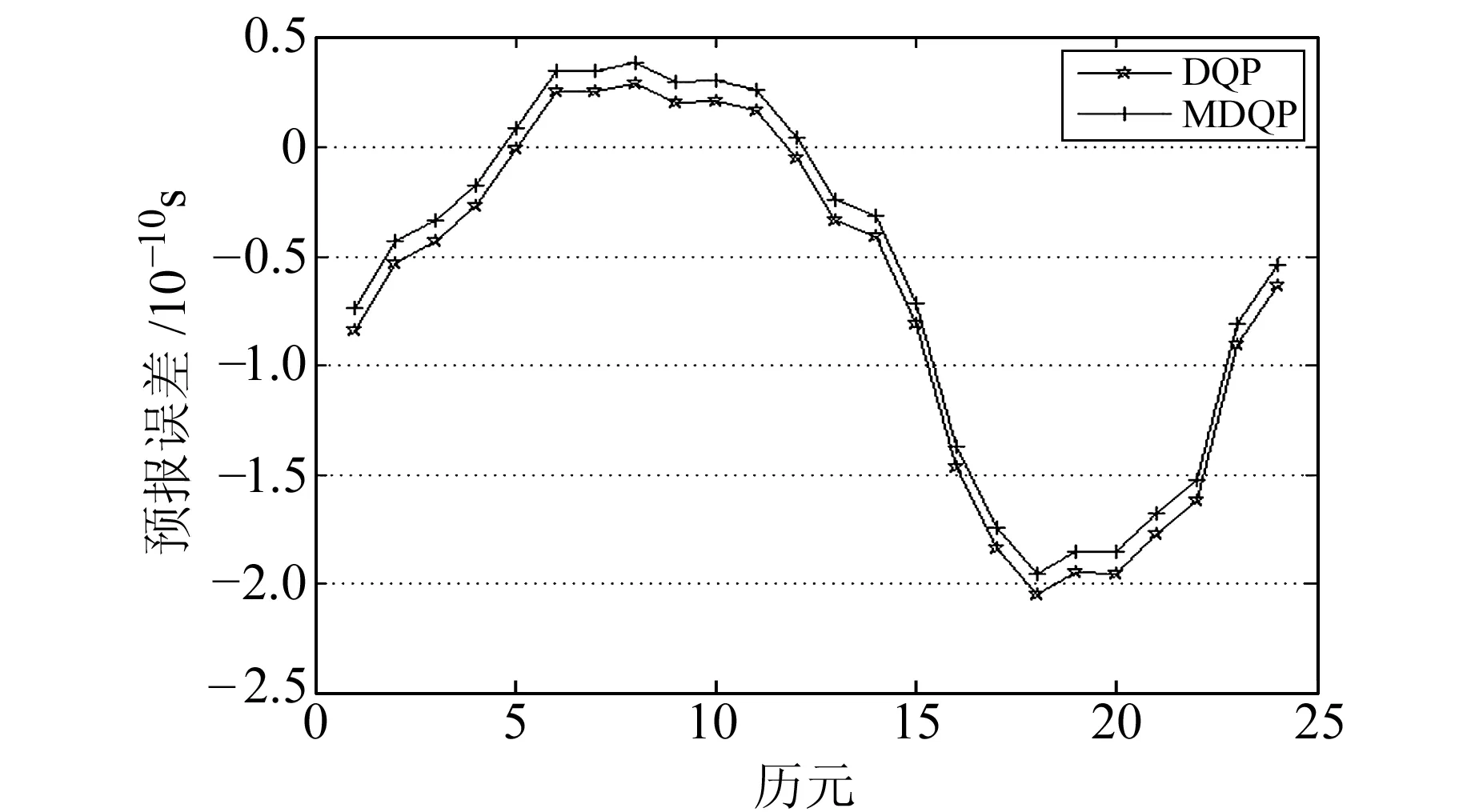
图5 加入0.1 ns粗差时预报结果的对比Fig.5 Comparison of prediction results during added outliers with 0.1 ns

由图表可以看出，MDQP模型的预报残差及RMS值均小于DQP模型，说明改进后的钟差一次差分预报原理能够在一定程度上改善最后一个建模数据不可靠对预报结果的影响，从而降低对最后一个建模钟差数据的依赖程度。

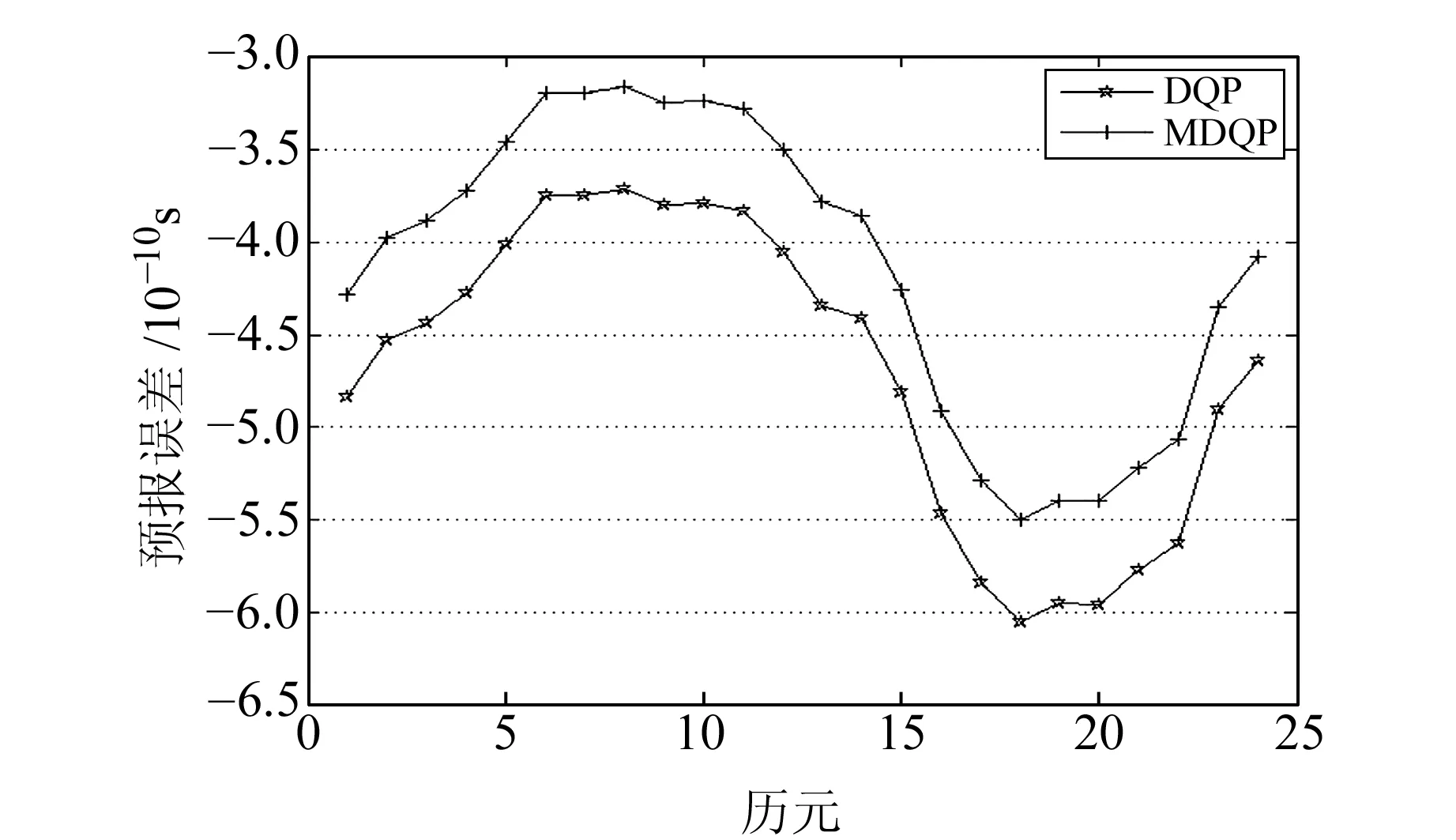
图6 加入0.5 ns粗差时预报结果的对比Fig.6 Comparison of prediction results during added outliers with 0.5 ns

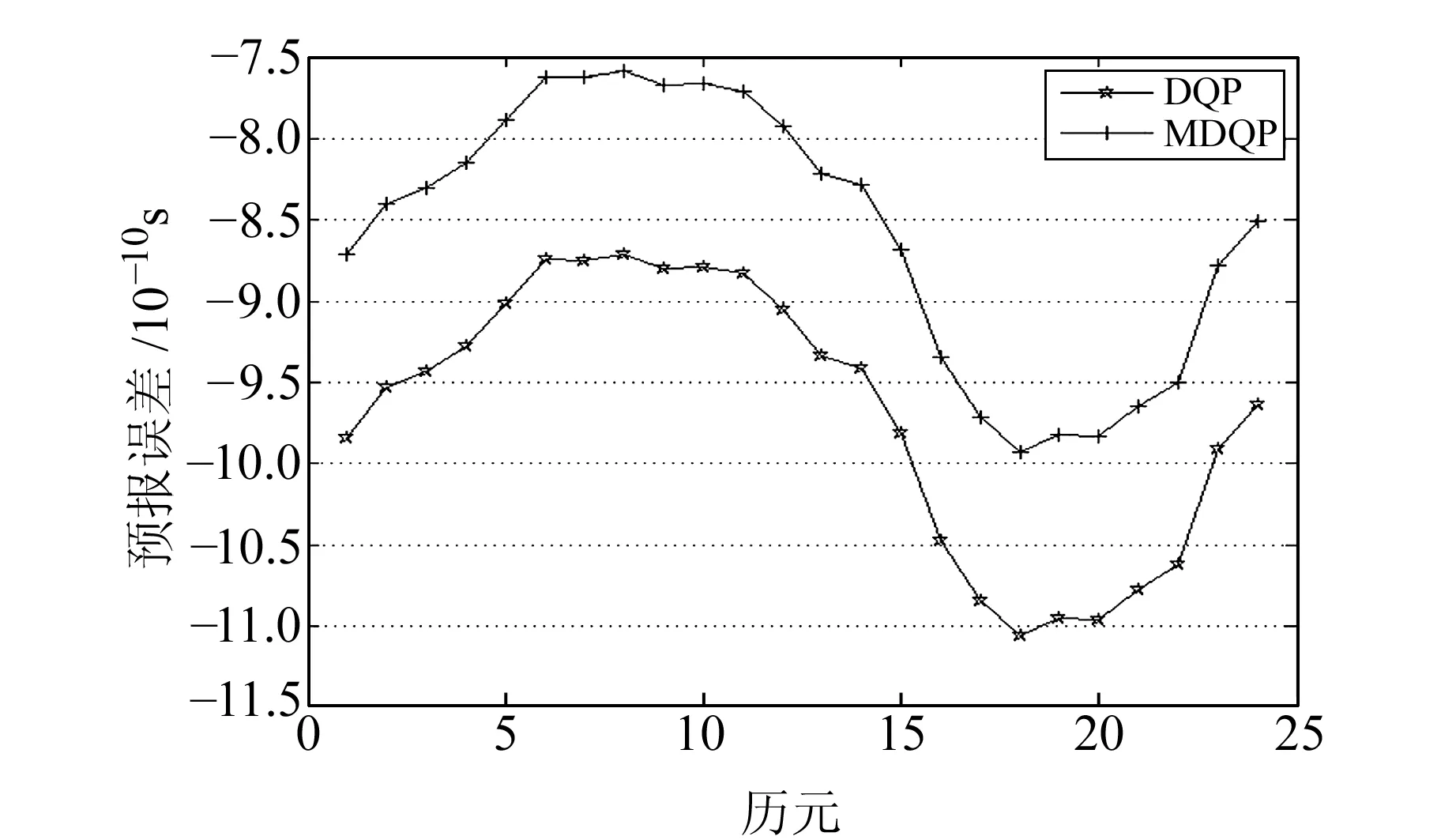
图7 加入1.0 ns粗差时预报结果的对比Fig.7 Comparison of prediction results during added outliers with 1.0 ns

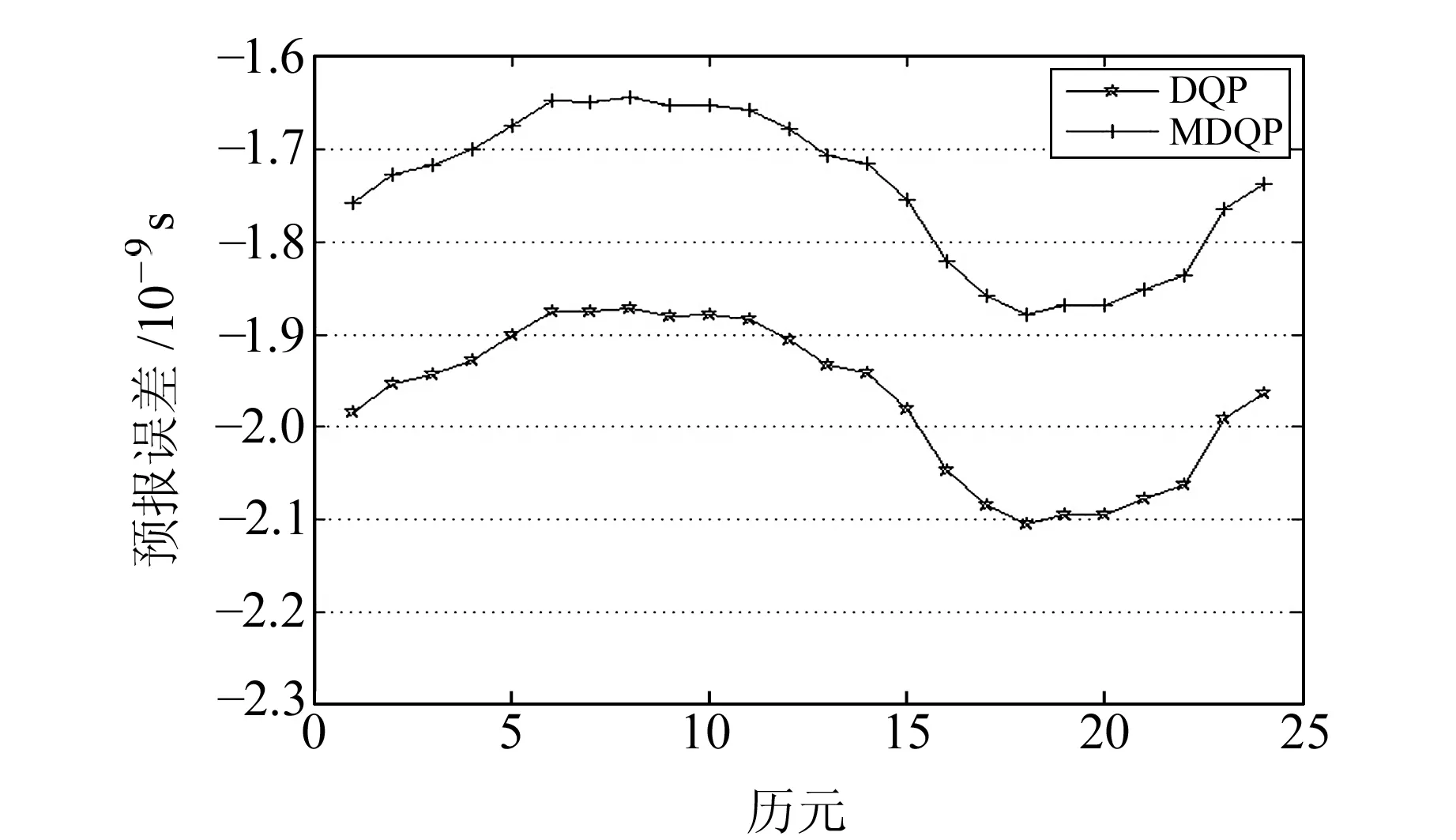
图8 加入2.0 ns粗差时预报结果的对比Fig.8 Comparison of prediction results during added outliers with 2.0 ns

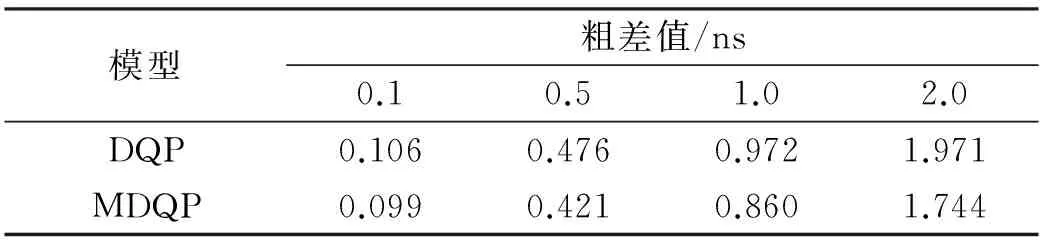
模型粗差值/ns0.10.51.02.0DQP0.1060.4760.9721.971MDQP0.0990.4210.8601.744

2 实验与分析

为了验证所提的基于钟差一次差分预报原理的有效性，采用IGS提供的GPS系统15 min采样间隔的精密钟差数据进行分析，数据采集时间为2015-04-04～04-18。考虑当前在轨运行的GNSS星载原子钟主要是铷原子钟，而该时间段内GPS星载铷(Rb)钟包含4种类型：BLOCKⅡA Rb钟、BLOCK ⅡR Rb钟、BLOCKⅡR-M Rb钟和BLOCKⅡF Rb钟。选取该时间段内数据完整的每种类型钟对应的一颗卫星，本文选取PRN01、PRN02、PRN04和PRN12进行预报实验。另外，以预报时间段对应的已知精密钟差值为参考真值，采用均方根误差(RMS)作为预报结果精度的统计量进行对比。均方根误差计算公式为：

(3)

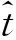
设计两种预报方案，通过对比常用的LP模型、QP模型和GM(1,1)模型在常规建模条件下的预报结果和基于改进的钟差一次差分原理的预报结果，分析基于钟差一次差分预报原理的特性。其中，基于改进的钟差一次差分预报原理的LP模型和GM(1,1)模型分别记作MDLP模型和MDGM模型，GM(1,1)模型简记为GM。使用前1 d的卫星钟差数据拟合后预报接下来6 h的钟差，连续预报14次。方案1，统计前4 h的预报精度；方案2，统计前6 h的预报精度。

图9～12分别给出了方案1中4颗卫星14次预报结果的RMS值。为了便于分析，表2和表3分别给出了4颗卫星在两种预报方案下各模型14次预报结果RMS的平均值及该平均值对应的4颗卫星的平均值。

分析图9～12、表2、表3可知：

1)对比LP、MDLP模型和QP、MDQP模型结果可以看出，两种预报方案下每颗卫星预报结果的RMS值都是MDLP模型小于LP模型、MDQP模型小于QP模型，说明MDLP模型比LP模型的预报精度高、MDQP模型比QP模型的预报精度高；对于4颗卫星预报精度的平均值而言，两种方案下MDLP模型较LP模型分别提高了25.5%和11.6%，MDQP模型较QP模型分别提高了17.7%和13.8%；而根据GM模型和MDGM模型的结果可知，4颗卫星预报精度的平均值，在两种方案下MDGM模型较GM模型分别提高了24.4%和11.0%。因此，在卫星钟差短期预报中，采用本文所提的修正钟差一次差分预报原理，可以提高常用的LP模型、QP模型和GM(1,1)模型的预报精度。

2)对比表2和3可以看出，MDLP模型、MDQP模型和MDGM模型在建模数据一定的条件下，随着预报时间的增长，模型预报结果的精度均有所降低。这3种模型中，MDLP模型在两种预报方案下的RMS值都最小，即MDLP模型的预报精度优于MDQP模型和MDGM模型，说明钟差一次差分数据更符合一次多项式模型。此外，根据各模型对4种类型卫星钟差预报的结果可知，基于改进钟差一次差分预报原理的预报结果与卫星钟的类型有关，特别是对于BLOCK ⅡF 型铷钟和ⅡR-M型铷钟，基于该预报原理可以更为显著地提高常规钟差预报模型的预报精度。

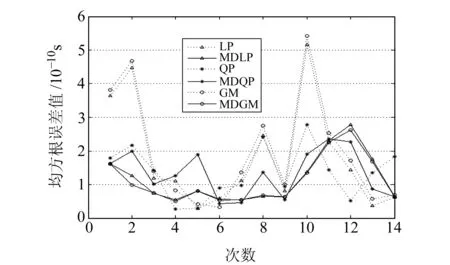
图9 PRN01卫星14次预报结果对应的RMS值Fig.9 RMS values of 14-time prediction results of satellite PRN01

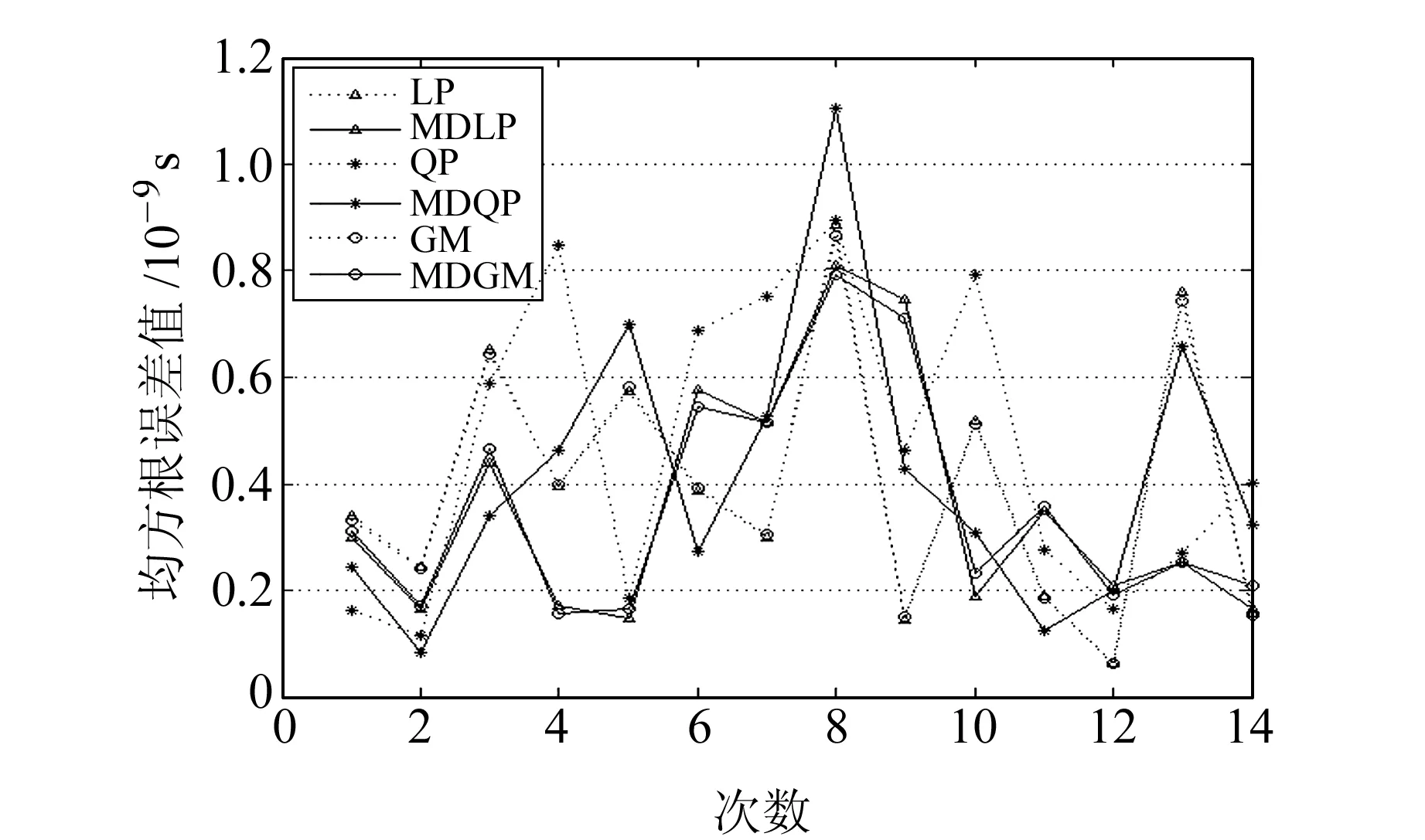
图10 PRN02卫星14次预报结果对应的RMS值Fig.10 RMS values of 14-time prediction results of satellite PRN02

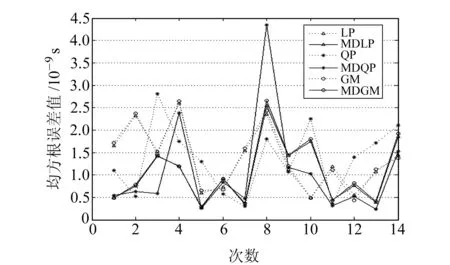
图11 PRN04卫星14次预报结果对应的RMS值Fig.11 RMS values of 14-time prediction results of satellite PRN04

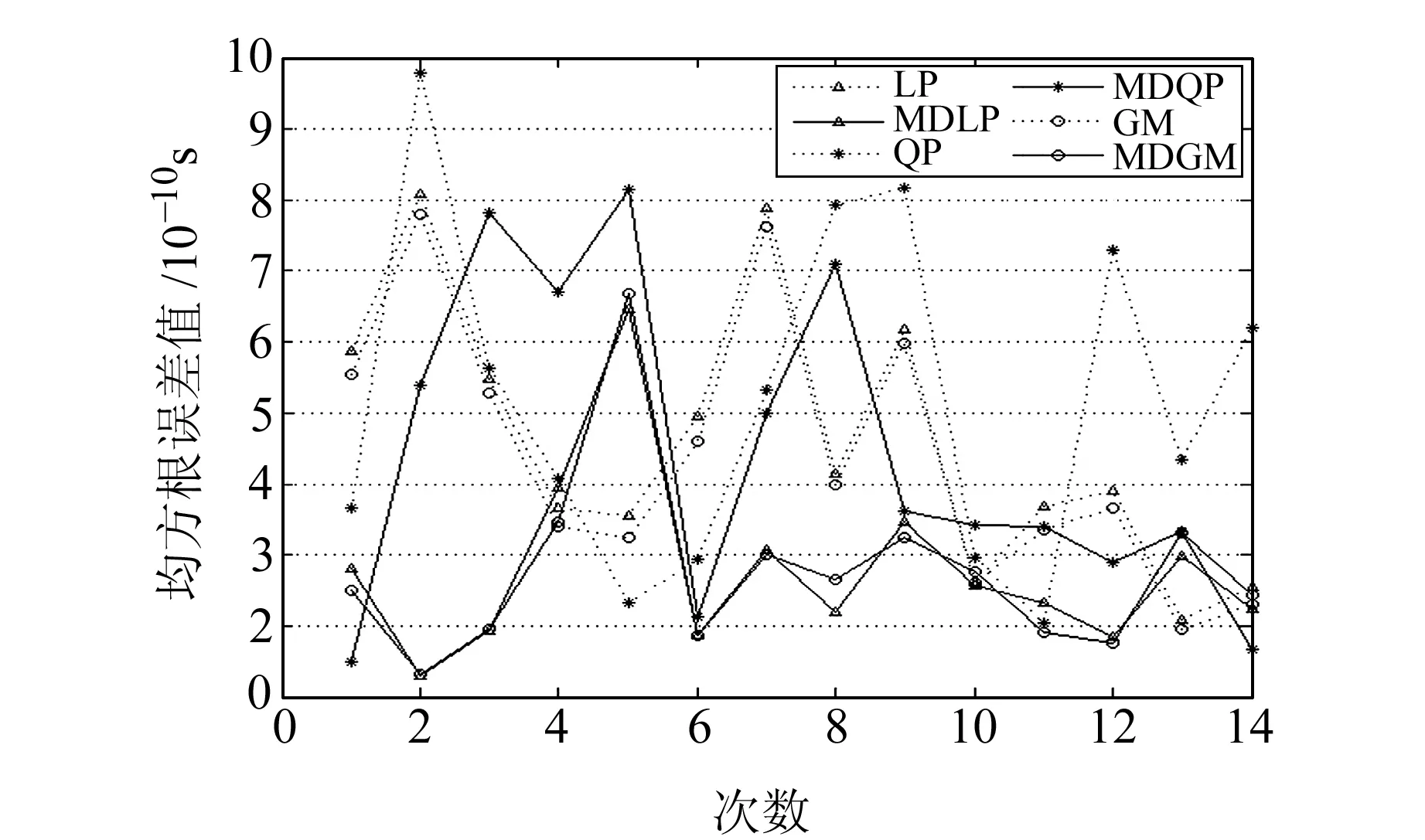
图12 PRN12卫星14次预报结果对应的RMS值Fig.12 RMS values of 14-time prediction results of satellite PRN12

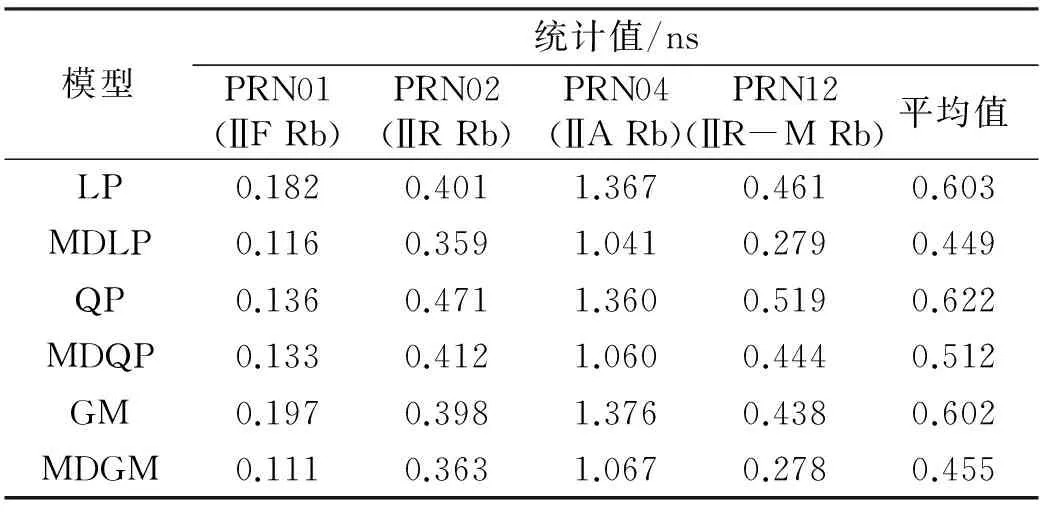
模型统计值/nsPRN01(ⅡFRb)PRN02(ⅡRRb)PRN04(ⅡARb)PRN12(ⅡR-MRb)平均值LP0.1820.4011.3670.4610.603MDLP0.1160.3591.0410.2790.449QP0.1360.4711.3600.5190.622MDQP0.1330.4121.0600.4440.512GM0.1970.3981.3760.4380.602MDGM0.1110.3631.0670.2780.455

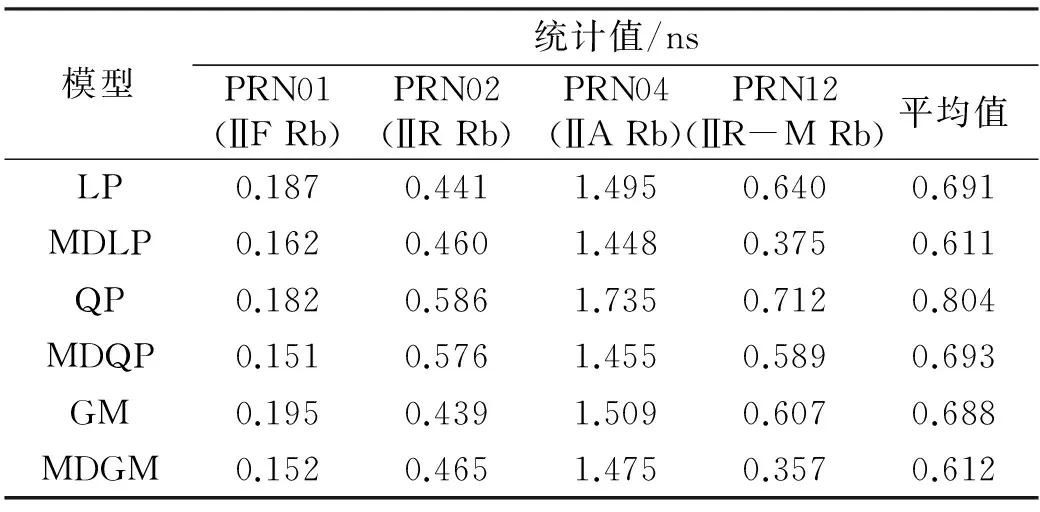
表3 6 h预报结果的统计值

3 结 语

本文通过对钟差数据进行一次差分实现钟差建模数据与建模策略的改变，研究基于钟差一次差分数据的卫星钟差预报方法来提高钟差预报的精度。实验表明，所提的改进的基于钟差一次差分预报原理能够在一定程度上改善最后一个建模数据含粗差时对预报结果的影响；采用基于修正钟差一次差分的预报原理，在钟差短期预报中可以提高常用钟差预报模型的预报精度，取得较常用模型更好的预报结果；对于卫星钟差的一次差分数据而言，更适合采用一次多项式模型建模。

[1] 王宇谱,吕志平,陈正生，等.卫星钟差预报的小波神经网络算法研究[J].测绘学报,2013,42(3):20-28(Wang Yupu，Lü Zhiping，Chen Zhengsheng, et al. Research the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013,42(3):323-330)

[2] 崔先强,焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报：信息科学版, 2005,30(5):447-450(Cui Xianqiang，Jiao Wenhai. Grey System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5):447-450)

[3] 郑作亚,党亚民,卢秀山，等.附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J].天文学报,2010,51(1):95-102(Zheng Zuoya, Dang Yamin, Lu Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sincia, 2010, 51(1):95-102)

[4] Heo Y J, Cho J, Heo M B. Improving Prediction Accuracy of GPS Satellite Clocks with Periodic Variation Behavior[J]. Measurement Science and Technology, 2010, 21(7): 3 001-3 008

[5] Senior K L, Ray J R, Beard R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3):211-225

[6] Davis J, Bhattarai S, Ziebart M. Development of a Kalman Filter Based GPS Satellite Clock Time-offset Prediction Algorithm [C]. European Frequency and Time Forum (EFTF), Gothenburg, Sweden, 2012

[7] 王宇谱,吕志平,宫晓春，等.一种新的钟差预处理方法及在WNN钟差中长期预报中的应用[J].武汉大学学报：信息科学版, 2016,41(3): 373-379(Wang Yupu，Lü Zhiping，Gong Xiaochun, et al. A New Data Preprocessing Method for Satellite Clock Bias and Its application in WNN to Predict Medium- and Long-term Clock Bias[J]. Geomatics and Information Science of Wuhan University, 2016,41(3): 373-379)

[8] 雷雨,赵丹宁.基于经验模式分解和最小二乘支持向量机的卫星钟差预报[J].天文学报,2014,55(3):216-227(Lei Yu, Zhao Danning. The Satellite Clock Bias Forecast Based on Empirical Mode Decomposition and Least Squares Support Vector Machines[J]. Acta Astronomica Sinica, 2014,55(3):216-227)

[9] 梁月吉,任超,杨秀发，等.基于一次差的灰色模型在卫星钟差预报中的应用[J].天文学报,2015, 56(3): 264-277(Liang Yueji, Ren Chao, Yang Xiufa, et al. Grey Model Based on First Difference in the Application of the Satellite Clock Bias Prediction[J]. Acta Astronomica Sinica, 2015, 56(3): 264-277)

[10]郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州: 信息工程大学, 2006(Guo Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellite[D]. Zhengzhou: Information Engineering University, 2006)

[11]黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D].西安: 长安大学,2012(Huang Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi’an: Chang ’an University, 2012)

About the first author:WANG Yupu, PhD candidate, majors in theory and method of satellite clock data processing, E-mail: 987834660@qq.com.

Satellite Clock Bias Prediction Based on Modified Single Difference Data of Clock Bias

WANGYupu1,2LÜZhiping1ZHOUHaitao1WANGNing1ZHAIShufeng1

1 School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China 2 State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi’an 710054, China

An improved strategy for the prediction principle based on single difference values of satellite clock bias (SCB) is proposed. This paper analyzes prediction characteristics of the frequently-used linear polynomial model, quadratic polynomial model and grey model when they use the proposed prediction principle. The simulation results show that the proposed improvement for the prediction principle is effective and the prediction precision of the frequently-used models can get better prediction results based on the proposed prediction principle in the short-term SCB prediction.

navigation satellite; clock bias prediction; single difference; data modeling

National Natural Science Foundation of China, No. 41674019; National Key Research and Development Program of China, No.2016YFB0501701; Open Fund of State Key Laboratory of Geo-Information Engineering, No. SKLGIE2015-M-1-6.

2015-12-23

项目来源：国家自然科学基金(41674019)；国家重点研发计划(2016YFB0501701)；地理信息工程国家重点实验室开放基金(SKLGIE2015-M-1-6)。

王宇谱，博士生，主要从事卫星钟数据的处理理论与方法研究，E-mail: 987834660@qq.com。

10.14075/j.jgg.2016.12.009

1671-5942(2016)012-1073-05

P228

A