霍尔效应测量磁场实验中副效应的研究

孙可芊，李 智，廖慧敏，张朝晖

(a.北京市八十中学，北京 100020； b.北京大学 物理学院，北京 100871)



霍尔效应测量磁场实验中副效应的研究

孙可芊a，李 智b，廖慧敏b，张朝晖b

(a.北京市八十中学，北京 100020； b.北京大学 物理学院，北京 100871)

用换向法对实验室的霍尔效应仪进行了测量，结果表明各种副效应中以不等位电势差的贡献最大，而能斯特效应和里吉-勒迪克效应的贡献可以忽略. 测量结果还显示存在一项额外的副效应，这一副效应与霍尔电流的平方成正比，与外磁场无关，其性质与一般教科书中提到的各种副效应都不同，应该是由霍尔电流的热效应引起的温差电动势. 根据上述结果，对换向法的公式进行了相应的修正.

霍尔效应；不等位电势差；温差电动势

霍尔效应是一种基本的电磁现象[1]. 根据霍尔效应制成的霍尔元件,在传感器、自动控制等领域有着广泛的应用[2-5]. 因此，利用霍尔效应测量磁场是大学物理实验中非常基本和常见的实验项目. 实际实验过程中，所测量的电压信号中，除了霍尔效应的贡献之外，还伴随着各种副效应的贡献[6-11]. 一般教科书上认为副效应主要包括不等位电势差、埃廷斯豪森效应、能斯特效应和里吉-勒迪克效应，这些副效应会对测量结果产生影响，因此实验中的重点内容就是通过换向法消除副效应. 然而，对实验中所用霍尔元件的测量结果表明：能斯特效应和里吉-勒迪克效应的贡献一般可以忽略，无需通过换向法消除，更为重要的是，实验中还存在另一项性质与前面所说的各种副效应都不同的副效应，这一项的影响一般不能忽略.

1 霍尔效应实验原理

将通有电流的导体置于垂直电流方向的外磁场中时，磁场会对导体中的运动电荷产生洛仑兹力，使电荷发生横向偏转，偏转的载流子在霍尔元件边界不断累积，并产生横向电场，直到横向电场力与洛仑兹力刚好互相抵消. 此时载流子不再偏转，在导体中垂直于外磁场和电流的方向上出现横向电势差UH，该现象称为霍尔效应. 根据霍尔效应的基本原理，霍尔电压UH与导体中通过的霍尔电流IH和垂直电流方向上所加的外磁场B成正比关系.

实际测量过程中还会伴随一些副效应，它们产生的附加电压将对UH的测量产生影响. 首先是不等位电势差，由于霍尔电压测量引线在制作时不可能绝对对称地焊接在霍尔片的两侧，因此，当霍尔电流IH流过霍尔元件时，即使不加外磁场，在霍尔电压测量引线间也会有电势差存在，这就是不等位电势差U0.U0与霍尔电流IH成正比，与外磁场B无关.

由于导体中载流子的速度满足一定统计分布，高速和低速载流子受到洛仑兹力和电场力的合力方向不同，将向相反方向偏转，并对霍尔片两侧造成不同效果的加热，使两侧出现温度差，进而产生温差电动势UE，这就是埃廷斯豪森效应. 埃廷斯豪森效应的电压UE与霍尔电流IH和外磁场B都成正比关系.

其次是能斯特效应，由于实际霍尔元件中霍尔电流引线两端电阻不完全相同，霍尔电流流过时发热不同，会产生一定的温度差，进而在霍尔电流所在方向上形成热流，而热流是由载流子的定向扩散运动形成的，因此，和电流类似，也会在外磁场B作用下产生横向的附加电压UN，这就是能斯特效应.UN与热流和外磁场B成正比，而热流由霍尔电流产生的热引起，与霍尔电流IH的平方成正比，因此UN与IH的平方成正比关系.

最后是里吉-勒迪克效应，类似于埃廷斯豪森效应中电流的载流子速度分布在磁场作用下会在横向产生温差电动势UE，热流的载流子速度分布在磁场作用下也会在横向产生温差电动势UR，这就是里吉-勒迪克效应.UR也与热流和外磁场B成正比，因此也和霍尔电流IH的平方成正比.

为消除副效应对霍尔电压测量的影响，常用的方法是换向法. 由于不同效应的电压对霍尔电流IH和外磁场B的依赖关系不同，改变IH和B的方向时，不同电压的符号改变不相同：

当IH正、B正时，

U1=UH+U0+UE+UN+UR;

(1)

当IH负、B正时，

U2=-UH-U0-UE+UN+UR;

(2)

当IH负、B负时，

U3=UH-U0+UE-UN-UR;

(3)

当IH正、B负时，

U4=-UH+U0-UE-UN-UR.

(4)

记下4种不同情况下的电压测量值U1,U2,U3,U4，并做运算可以得到

UH+UE=(U1-U2+U3-U4)/4,

(5)

U0=(U1-U2-U3+U4)/4 ,

(6)

UN+UR=(U1+U2-U3-U4)/4.

(7)

也就是可以分别获得UH+UE,U0和UN+UR的值. 这里换向法虽然不能消去与UH方向始终相同的UE，但由于UE和UH对霍尔电流IH和外磁场B的依赖关系完全相同，实际上可以不做区分，而不会对实验中磁场的测量结果造成影响.

2 实验内容和数据

实验使用西安理工大学科教仪器研究所研制开发的HL-4霍尔效应仪(见图1). 外磁场B由电磁铁产生，其大小和方向可以通过改变励磁电流IM的大小和方向进行控制，霍尔片置于电磁铁的气隙中. 实验中首先将IM的大小固定在0.600 A，再依次将霍尔电流IH的大小设定为2.000,4.000,6.000,8.000,10.000 mA. 每次都通过换向开关1和换向开关3分别改变霍尔电流IH和励磁电流IM(从而改变外磁场B的方向)的方向，用数字电压表测出霍尔元件两端相应的4组电势差数据U1,U2,U3,U4，并根据式(5)～(7)计算出UH+UE,U0和UN+UR的值，结果如表1所示. 这里，由于式(5)～(7)中都包含“除以4”，将计算得到的电压值多保留了1位数字.

图1 实验装置图

IH/mAU1/mVU2/mVU3/mVU4/mV(UH+UE)/mVU0/mV(UN+UR)/mV2.0009.96-9.988.97-8.999.4750.4950.0004.00020.05-20.1217.92-18.0019.0221.0620.0026.00030.06-30.2326.87-27.0428.5501.5950.0008.00040.06-40.3635.80-36.0938.0782.132-0.00210.00050.06-50.5444.73-45.1947.6302.670-0.005

为了更直观地显示出不同效应电压的相对大小和所满足的基本规律，在图2中分别画出了UH+UE，U0和UN+UR对IH的依赖关系. 由图2可以看到：UH+UE和U0都与霍尔电流IH成正比关系，与理论预言的规律一致；而U0的大小大约是UH+UE的6%，也就是说不等位电势差的贡献比较明显，不能忽略. 相比之下，从表1中可以看到，当IH变化时，UN+UR表现为随机涨落，并且绝对值始终在0.01 mV以下，也就是说在仪器分辨能力范围内(数字电压表200 mV挡分辨率为0.01 mV)，没有观察到明显的UN+UR.

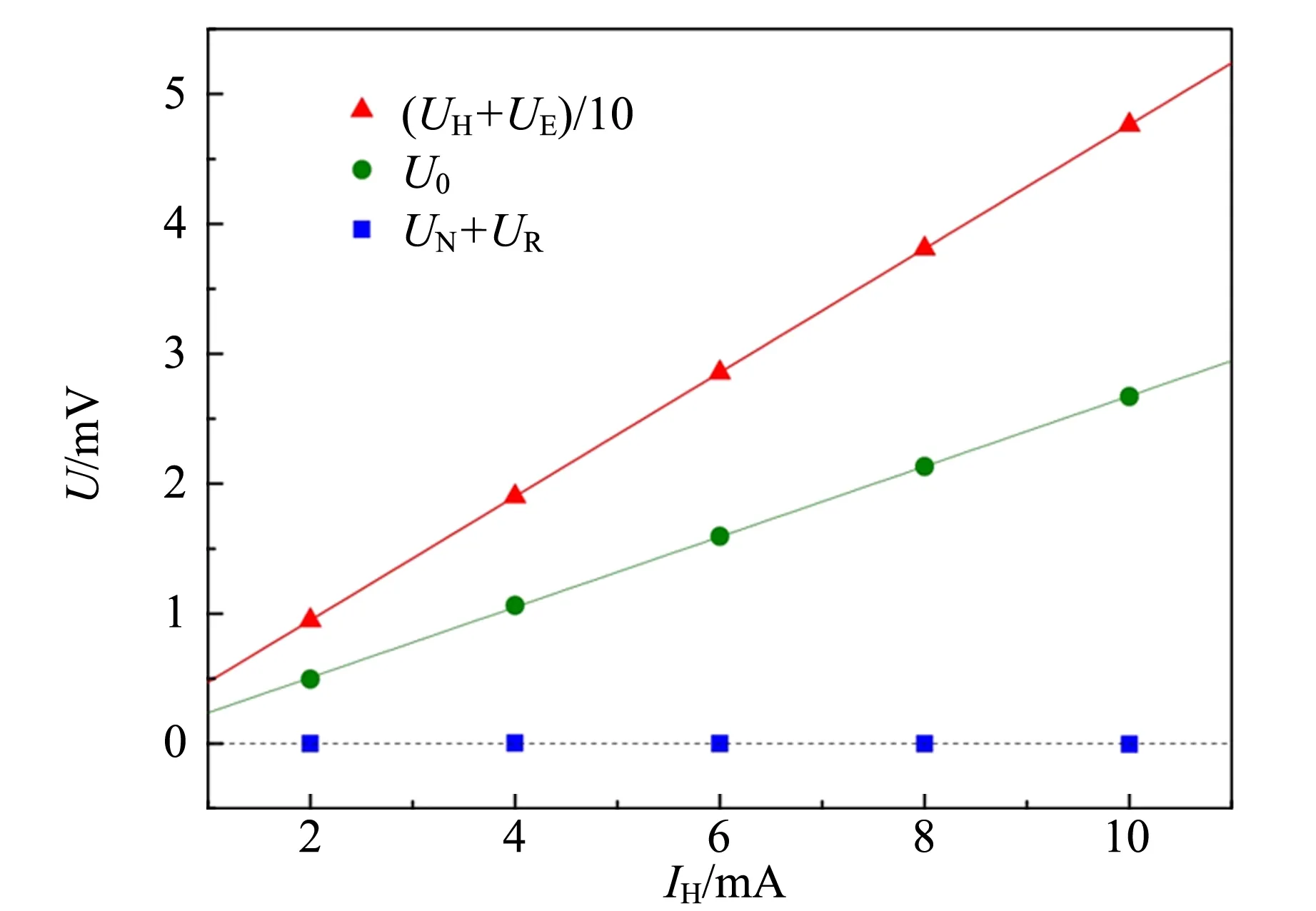
图2 UH+UE，U0和UN+UR对霍尔电流IH的 依赖关系(励磁电流IM=0.600 A)

由于测量结果显示UN+UR可以忽略，即UN+UR≈0，代入式(1)～(4)可以得出U1≈-U2，U3≈-U4. 然而观察表1中的原始测量数据可以发现，上述关系并不成立，U1与-U2、U3与-U4之间存在明显偏差. 为了更清楚地显示出这一差异，将U1-(-U2)(即U1+U2)和U3-(-U4)(即U3+U4)的计算结果列入表2中，可以看到U1+U2与U3+U4的值近似相等并且随霍尔电流IH的增加而增加. 这一结果说明:在式(1)～(4)中一定还存在着之前没有考虑到的其他副效应. 这一额外副效应随霍尔电流IH的增加而增加，但增长速度明显快于IH. 在图3中，画出了U1+U2和U3+U4对IH平方的依赖关系，可以看到二者与IH的平方呈正比关系. 根据这一特征猜测这一副效应应该是由霍尔电流的焦耳热效应所导致的，因此与霍尔电流的平方成正比.

表2 U1-(-U2)和U3-(-U4)对霍尔电流IH的

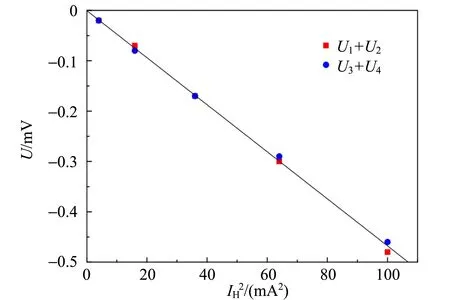
图3 U1+U2和U3+U4对IH平方的依赖关系 (励磁电流IM=0.600 A)

为了进一步弄清楚这一额外副效应的来源，将霍尔电流IH的大小固定在10.000 mA，依次改变励磁电流IM，从而改变外磁场B的大小(外磁场B近似与励磁电流IM成正比关系，如表3所示)，测量U1～U4随励磁电流的变化，并对测得的数据进行与之前类似的处理. 为了简单起见，省略了部分原始测量数据，而在表3中直接给出计算得到的各个电压项.

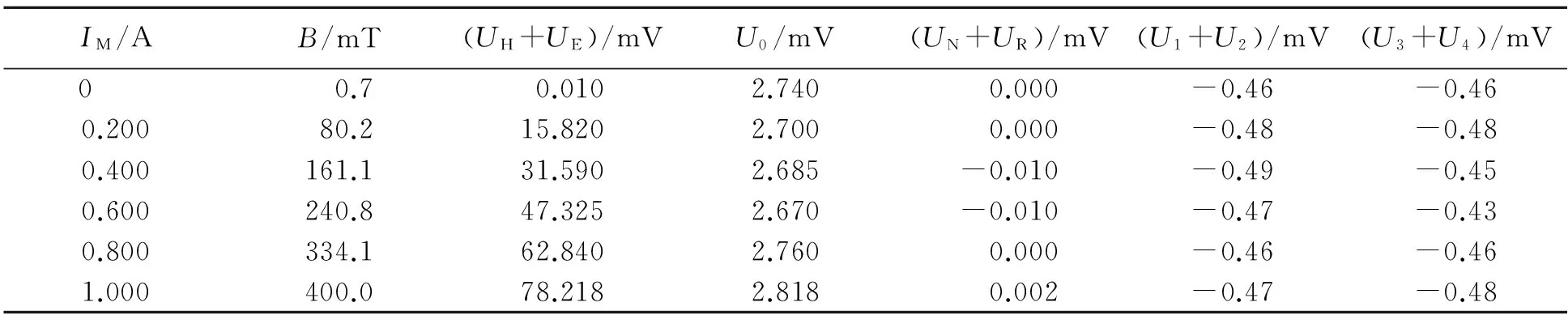
表3 固定IH=10.000 mA，改变励磁电流IM，由测量结果计算得到的不同电压项

可以看到，UH+UE与励磁电流IM或者说外磁场B大致成正比关系，与理论预期一致. 不等位电势差U0的大小始终保持在2.7 mV左右，与外磁场B基本无关，也和理论预期一致.UN+UR的绝对值始终不超过0.01 mV，并且与外磁场B没有表现出明显的依赖关系，也就是说在仪器分辨能力范围内没有观察到明显的UN+UR，这一结果也和之前固定IM改变霍尔电流IH情况下的结果保持一致.U1+U2和U3+U4这两项始终保持近似相等并且不随励磁电流变化而改变，由此可以得出结论，这一额外副效应与外磁场B无关.

综合前面改变霍尔电流和励磁电流的实验结果可得出结论：存在一项额外的副效应，这一副效应与外磁场B无关，而与霍尔电流IH的平方呈正比关系. 基于这2个特征，我们认为这一副效应应该是霍尔电流所引起的温差电动势：当霍尔电流流过霍尔片时，会产生焦耳热，由于两侧霍尔电压引线的焊点不可能完全相同，焊点附近霍尔电流的发热和散热能力存在差别，因此2个霍尔电压引线间温度不可能完全相同，这一效应会导致2个引线间存在一定的温度差，进而由于温差电效应会产生额外的温差电动势UT，这一电动势的产生与外磁场B无关，是纯粹的电效应，同时由于是霍尔电流的焦耳热引起的，所以和霍尔电流的平方成正比.

考虑到额外副效应UT的存在，需要对式(1)～(4)进行修正. 由于UT与霍尔电流的平方成正比，也就是说与霍尔电流的方向无关，同时UT又与外磁场B无关，因此，对于一定大小的霍尔电流，在改变霍尔电流和励磁电流的方向时，副效应UT始终保持不变，相当于是常数项，这一性质明显不同于其他已知的各项副效应，由此可以得到修正后的实际测量电压公式：

当IH正、B正时，

U1=UH+U0+UE+UN+UR+UT;

(8)

当IH负、B正时，

U2=-UH-U0-UE+UN+UR+UT;

(9)

当IH负、B负时，

U3=UH-U0+UE-UN-UR+UT;

(10)

当IH正、B负时，

U4=-UH+U0-UE-UN-UR+UT.

(11)

对修正后的公式做运算可以得到，式(5)～(7)仍然成立，也就是说，副效应UT的存在不影响UH+UE,U0和UN+UR的计算. 原因是UT在修正后的式(8)～(11)中表现为常数项，在不同电压的减法运算中互相抵消，因此不影响UH+UE,U0和UN+UR的计算. 但是副效应UT的存在会使实验中的4个测量电压U1～U4在整体上发生相同的偏移. 根据式(8)～(11)还可以得到UT的计算公式为

UT=(U1+U2+U3+U4)/4.

(12)

在图4中给出了计算得到的UT随外磁场B的变化，可以看到UT近似保持不变，也就是与外磁场B无关. 作为对比，图中还给出了U0和UN+UR，可以看到不等位电势差U0也和外磁场B无关，并且在这3种副效应中，U0最为显著，其次是UT，而UN+UR可以忽略.

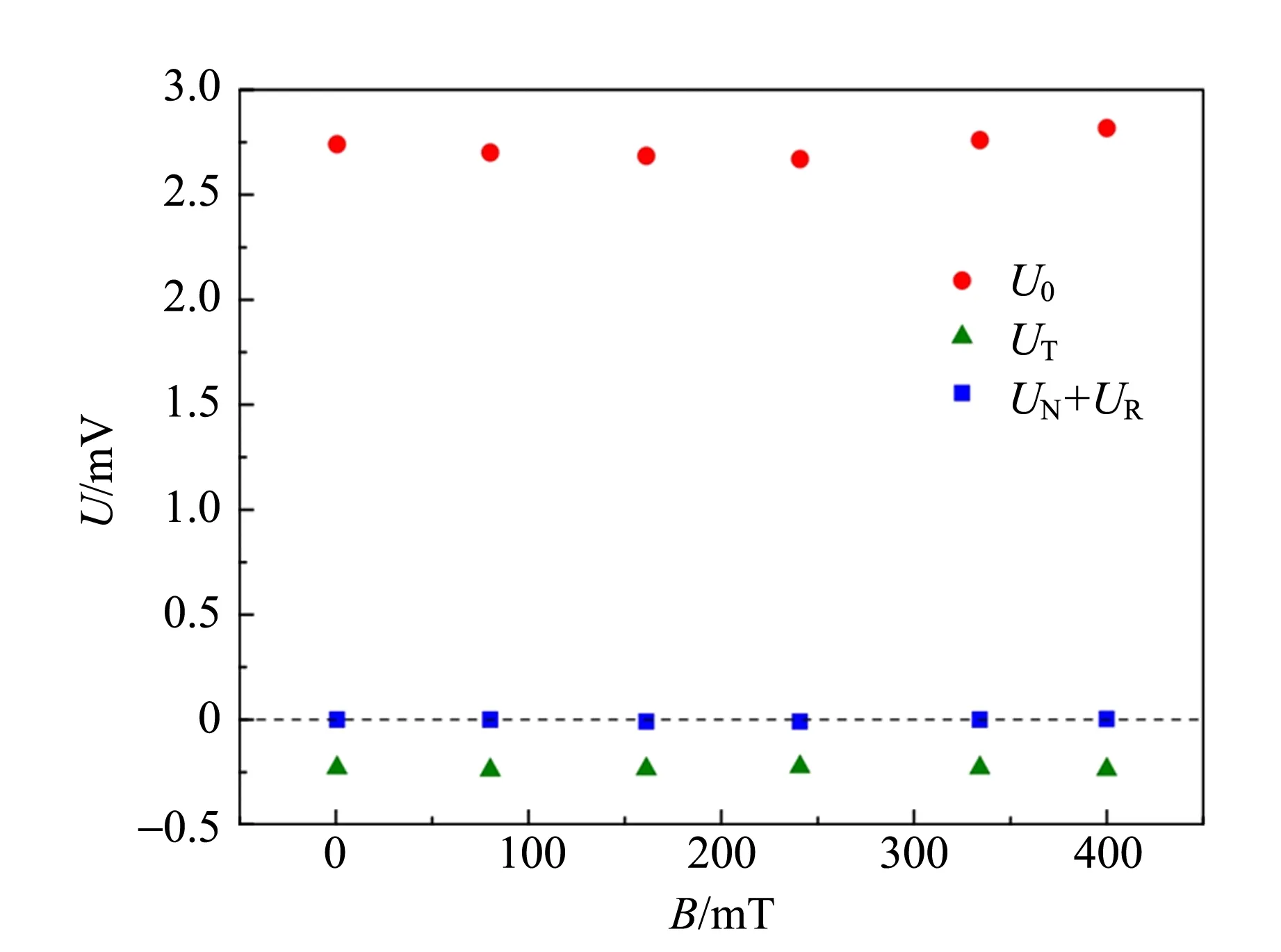
图4 利用修正后的公式计算得到的U0,UT和UN+UR 对外磁场B的依赖关系

以上是实验室中某个霍尔元件的测量结果，为了验证结论的普遍性，又在实验室中任意选取了其他5台仪器进行测量. 表4列出了在霍尔电流IH=10.000 mA、励磁电流IM=1.000 A的情况下，用上述修正后的公式计算所得到的不同效应的电压值. 从结果可以看出，副效应基本都是以不等位电势差U0最为明显，大致是在UH+UE的百分之几量级；其次是霍尔电流产生的温差电动势UT，大致在UH+UE的千分之几量级；而能斯特效应和里吉-勒迪克效应对应的电压UN+UR比UT小1个量级以上，基本可以忽略. 也就是说，前面实验中所观测到的主要现象是普遍存在的.

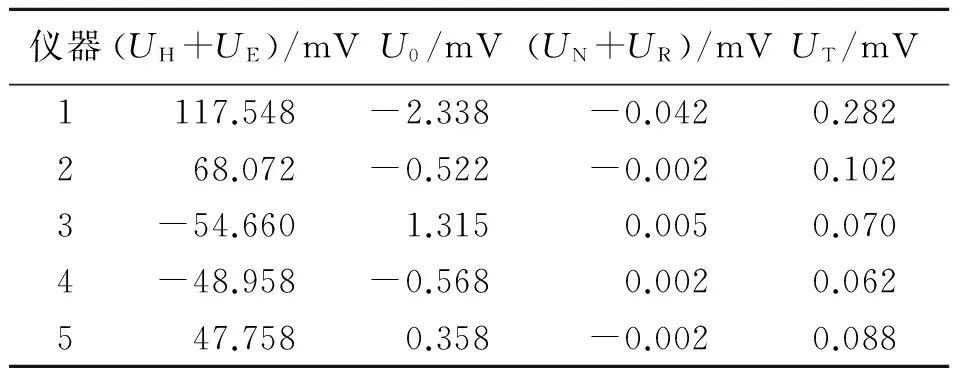
表4 用修正后的公式测量、计算得到的其他5台仪器的

不等位电势差U0是由霍尔电压测量引线的不对称所引起的，受到仪器制作工艺的限制，上述现象应该普遍存在，因此副效应中通常以U0最为明显是合理的现象. 由于霍尔电压引线的焊点不可能完全相同，焊点附近霍尔电流的发热和散热能力存在差异，在霍尔电流的焦耳热作用下，导致霍尔电压测量引线间存在温度差也是很正常的现象，而温差电动势UT是上述温度差所直接产生的电动势，这一效应较为显著也是比较合理的. 相比之下，能斯特效应和里吉-勒迪克效应的产生需要在霍尔电流的焦耳热作用下，使电流引线间先产生温度差，并进一步由这一温度差引起热流存在，再由热流载流子在磁场下偏转产生电压UN+UR，这是一种次生的高阶效应，因此一般来说UN+UR比霍尔电压引线间的温度差所直接产生的温差电动势UT要弱得多. 查阅资料可以发现，能斯特效应和里吉-勒迪克效应一般都描述为热流在外磁场作用下所产生的电动势，可以想象，上述效应在没有电流只有热流的情况下会相对较为显著，而在霍尔效应实验中，热流本身只是电流产生的次生效应，因此不难理解，这种情况下次生的热流所引发的电动势相对于电流直接产生的电动势来说一般是可以忽略的，这就是实验中没有观察到明显的UN+UR的原因.

另外为什么长期以来副效应UT并未引起关注？从教学实践来看，主要原因是容易将温差电动势UT误认为是UN+UR. 如果从一般教科书上的公式，也就是式(1)～(4)出发，会认为UN+UR存在的后果是使U1与-U2,U3与-U4之间产生差异，也就是在霍尔电流换向时测量的电压值会表现出差异，并且这一差异也是与霍尔电流IH的平方成正比，因此，如果不做深入分析，很容易直接认为测量数据中U1与-U2，U3与-U4之间的差异是源于UN+UR. 然而，从修正公式(8)～(11)来看，副效应UT同样会使U1与-U2，U3与-U4之间出现差异. 那么如何区分UT和UN+UR所造成的差异呢？关键不同在于UT与外磁场B无关，而UN+UR与B成正比. 从表3中的数据来看，实验中U1-(-U2)和U3-(-U4)都与B无关，说明这个差异是源于UT而非UN+UR. 此外，从修正公式还可以分析出，若只有UT存在会使U1-(-U2)和U3-(-U4)的大小、符号都相同；反之，若只有UN+UR存在则会使U1-(-U2)和U3-(-U4)大小相等、符号相反，而表2和表3中的数据表明，实验中的实际情况属于前者，这也是区分UT和UN+UR的一种办法.

3 结束语

利用换向法对实验室的霍尔效应仪进行了测量，结果表明副效应中不等位电势差的贡献最大，而能斯特效应和里吉-勒迪克效应可以忽略. 此外，实验结果表明还存在额外的副效应，这种副效应与霍尔电流的平方成正比，与外磁场无关，其性质与一般教科书中提到的各种副效应都不同，应该是由霍尔电流的焦耳热所引起的温差电动势. 实际教学当中，容易将此副效应误认为是能斯特效应和里吉-勒迪克效应，因此需要特别注意.

[1] 吕斯骅，段家忯，张朝晖. 新编基础物理实验[M]. 北京：高等教育出版社，2013：197.

[2] 吴高米，崔敏，王闯，等. 利用霍尔元件测量金属丝的弹性模量[J]. 物理实验，2014，34(6)：40-42.

[3] 张立辉，张攀，乐宏昊. 利用双霍尔探头测螺线管中低频交变磁场[J]. 物理实验，2014，34(7)：30-32.

[4] 王科范，刘平安. 利用霍尔效应研究热退火对黑硅材料电学性质的影响[J]. 物理实验，2014，34(10)：1-3.

[5] 徐雅惠，周林，李欣蔚，等. 基于霍尔效应的惯性测振实验的研究与应用设计[J]. 物理实验，2015，35(7)：35-39.

[6] 刘昶丁，柳纪虎. 霍尔效应中的副效应及其消除方法[J]. 物理实验，1987，7(1)：1-3.

[7] 李文成，王涌萍. 霍耳效应测量磁场实验中的副效应及温度对测量结果的影响[J]. 大学物理，1995，14(5)：36-38.

[8] 刘晓云. 霍尔效应实验直流测量法的误差探讨及处理[J]. 大学物理实验，2004，17(2)：58-61.

[9] 董海鹏. 热磁副效应的消除是必要的吗[J]. 牡丹江大学学报，2008，17(12)：98-100.

[10] 杨洁. 霍尔效应测量半导体特性参数中副效应的消除方法[J]. 三维坊学院学报，2010，10(6)：32-34.

[11] 黄响麟，何琛娟，廖红波，等. 变温霍尔效应中副效应的研究[J]. 大学物理，2011，30(3)：48-52.Associated effects in experiment of measuring magnetic field with Hall effect

[责任编辑：郭 伟]

SUN Ke-qiana, LI Zhib, LIAO Hui-minb, ZHANG Zhao-huib

(a. Beijing No.80 High School, Beijing 100020, China;b. Shool of Physics, Peking University, Beijing 100871, China)

Contributions of different associated effects to the Hall voltage were determined in the experiment of measuring magnetic field with Hall effect. It was found that the influence of IR drop was prominent, while the contributions of the Nernst and Righi-Leduc effects were negligible. The results also indicated the presence of an additional associated effect, which was proportional to the square of the Hall current and was independent of the magnetic field. This effect was attributed to thermo-electromotive-force originating from the thermal effect of the Hall current.

Hall effect; IR drop; thermo-electromotive force

2016-06-18

中学生英才计划

孙可芊(1999-)，女，北京人，北京市八十中学学生.

O472.6

A

1005-4642(2016)11-0036-05