磁性薄膜的有效垂直磁各向异性场的全输运测量

石弼钊

(中国人民大学附属中学，北京 100080)



磁性薄膜的有效垂直磁各向异性场的全输运测量

石弼钊

(中国人民大学附属中学，北京 100080)

采用磁控溅射方法，通过金属掩膜板制备了霍尔棒形状“CoFeB/MgO”体系薄膜样品，其中CoFeB层厚度为1.0 nm、1.1 nm、1.2 nm，利用垂直温度梯度的反常能斯特效应和反常霍尔效应对其相关磁输运特性进行了测量，所得结果可分别等效为常规面内和垂直方向的磁滞回线，并由此获得了薄膜的有效垂直各向异性场.

反常霍尔效应；反常能斯特效应；磁性薄膜；有效垂直磁各向异性场；全输运测量

具有垂直磁各向异性的磁性多层膜一直是磁性薄膜研究的热点. “CoFeB/MgO”体系组成的多层膜材料是近年来发现的一种新型垂直磁各向异性多层膜. 研究表明，当CoFeB厚度在1.0～1.2 nm时，Ta/CoFeB/MgO及MgO/CoFeB/Ta薄膜具有强的垂直各向异性[1].

所谓垂直磁各向异性，即为磁化过程中垂直薄膜表面外磁场所做的功小于平行膜面外磁场时所需要做的功，也就是说，垂直于薄膜表面的磁化相对较为容易. 有效垂直磁各向异性场为有效垂直磁各向异性能的一种等价表现形式，是表征磁性薄膜最重要的物理参量和性能指标，原则上在忽略磁畴影响的情形下，可通过测量平行膜面和垂直膜面的磁滞回线获得. 一般采用振动样品磁强计(VSM)、超导量子磁强计(SQUID)等进行测量[2-5]. 这些大型测量设备比较昂贵，且对于超薄膜情形，样品的总磁矩小，接近或甚至小于极限灵敏度，测量有效垂直磁各向异性场变得比较困难.

由于输运测量对样品总磁矩的依赖性并不高，譬如人们往往通过测量反常霍尔回线来等效表现垂直薄膜方向的磁化曲线，这样可不受薄膜厚度的限制. 不过，由于反常霍尔效应对电流、磁场及电压3个方向互相垂直的要求，面内方向的磁化曲线依然无法从类似的磁输运而获得. 本文提出：通过在垂直膜面方向加一温度梯度，进而通过测量反常能斯特效应电压随面内磁场的变化，可获得膜面内的等效磁化曲线. 本论文结合反常霍尔效应和反常能斯特效应测量，采用全输运的方式对CoFeB薄膜的有效垂直磁各向异性场进行测量.

1 相关理论简述

1.1 反常霍尔效应理论

在置于xy平面内的非磁性金属或半导体薄片中，若沿x轴方向施加一外电场E，沿z轴(薄片所在平面的法线方向)施加一外磁场B，此时材料中的载流子在外加电场所受电场力而沿x轴方向运动的同时，还受到外加磁场的洛伦兹力作用在y轴方向发生横向附加运动，载流子轨迹发生一定偏转，使得薄片两侧电荷积累，从而产生霍尔电压VH，当其处于稳定状态时，载流子受到霍尔电压产生的电场力与洛伦兹力平衡，轨迹不再发生偏转. 而此时，横向霍尔电阻率ρxy的大小与外加磁场B的大小成正比，即

ρxy=R0B,

(1)

其中，R0为常规霍尔系数，其大小与载流子数目成反比，其符号取决于载流子的类型. 此现象称为正常霍尔效应(OHE).

而对于具有铁磁性的金属样品，横向电阻率ρxy在(1)式常规项的基础上又引入了与样品磁化强度M有关的反常项，在样品达到饱和磁化强度Ms时，此反常项大小变为常量. 一般地，在样品未达到饱和磁化强度之前，ρxy随着外磁场B的大小的增加而迅速增加，之后经过一拐点后继续随外磁场B缓慢线性增加. 其拐点即为样品恰好达到饱和磁化强度Ms的情况. 显然，仅利用载流子在外磁场中所受洛伦兹力并不能对此现象进行合理地解释，因而称之为反常霍尔效应(AHE). 根据经验，一般将反常霍尔效应的横向电阻率ρxy写作：

ρxy=R0B+4πRsM,

(2)

其中，Rs称为反常霍尔系数，通常其大于正常霍尔系数R0至少1个量级以上，且对温度有强烈的依赖性[6].

反常霍尔效应来自内禀和外禀机制. 内禀机制认为，由于自旋-耦合轨道，动量空间布洛赫波函数的贝里曲率决定了霍尔电导率. 在理想晶体中，利用布洛赫波函数组成的波包表示晶体载流子在外加电磁场中的准经典运动，可以得到反常速度与外磁场B无关，其方向与外加电场E垂直. 在完整的布里渊区内，通过积分所有占据能带的贝里曲率，可得出晶体的反常霍尔电导率：

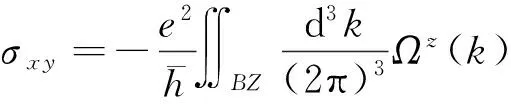
(3)

其中，k为波矢. 外禀机制主要来自各类杂质相关的散射，包括斜交和侧跃2种具体机制[7].

1.2 反常能斯特效应理论

在置于xy平面内的非磁性金属或半导体薄片中，若沿x轴方向施加温度梯度T，沿z轴(薄膜所在平面的法线方向)施加外磁场B，此时由于温度梯度的存在，载流子产生扩散运动，同时，载流子还将受外加磁场的洛伦兹力的作用，运动轨迹因而发生一定的偏转，使得薄片两侧电荷积累，从而产生能斯特电压VN，当其处于稳定状态时，载流子受到能斯特电压产生的电场力与洛伦兹力平衡. 对于温度梯度恒定的体系，能斯特电场有如下表达：

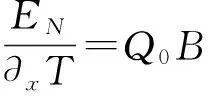
(4)

其中，Q0为正常能斯特系数，能斯特电场场强EN与载流子类型与温度场、磁场方向有关. 此现象被称为(常规)能斯特效应.

与霍尔效应类似，对于具有铁磁性的金属样品，能斯特电场在正常项的基础上又加入了与样品磁化强度M有关的反常项，在样品达到饱和磁化强度Ms时，其反常项大小就变为常量. 一般地，对于温度梯度恒定的体系，在样品未达到饱和磁化强度之前，能斯特电场场强EN随着外磁场B的大小的增加而迅速增加，之后经过一拐点后继续随外磁场B缓慢线性增加. 其拐点即为样品恰好达到饱和磁化强度Ms的情况. 显然，仅利用载流子在外磁场中所受洛伦兹力并不能对此现象进行合理地解释，因而人们称之为反常能斯特效应(ANE). 根据经验，一般将能斯特电场与温度梯度(塞贝克系数S)的比值写作：

(5)

其中，Qs称为反常能斯特系数，在铁磁性材料中，广泛存在Qs≫Q0. 反常能斯特效应的机理类似反常霍尔效应，但更为复杂.

2 薄膜样品制备

2.1 基片的选择、清洗与装片

单晶硅片(单面抛光)作为薄膜样品的基片，切割尺寸为5 mm×7 mm. 硅基片的清洗过程如下：

1)将硅片在洗液中浸泡24 h以上. 洗液的配比为：10 g K2Cr2O7+200 mL H2SO4(浓)+25 mL H2O.

2)分别用丙酮和无水乙醇超声清洗30 min.

3)用去离子水超声清洗2次，每次15 min.

4)用匀胶机将基片甩干，备用.

为了便于测量，选择霍尔棒形状掩膜板进行装片. 在装片之前，用无水乙醇对掩膜板与卡箍等进行清洗. 装片完成后用氮气冲喷基片表面，并将掩膜板与基片安装到样品位上.

2.2 薄膜样品的参量选择

在样品设计上，采用“Ta/CoFeB/MgO”典型结构. 综合薄膜界面效应的影响并结合以往对于CoFeB和MgO层厚度的研究，具体如下：

Si/Ta (5 nm)/ CoFeB(1.0 nm)/MgO(2 nm)/Ta(3 nm)；Si/Ta (5 nm)/ CoFeB(1.1 nm)/MgO(2 nm)/Ta(3 nm)；Si/Ta (5 nm)/ CoFeB(1.2 nm)/MgO(2 nm)/Ta(3 nm).

2.3 磁控溅射

本研究的薄膜样品采用磁控溅射的物理沉积方法(PVD). CoFeB靶与MgO靶采用射频溅射，Ta靶则利用直流溅射. 溅射台的背景真空4.6×10-5Pa，氩气压pAr=0.5 Pa，Ta靶溅射速度0.061 1 nm/s，CoFeB靶溅射速度0.083 3 nm/s，MgO靶溅射速度0.021 5 nm/s. 薄膜各层的厚度由基片在对应溅射靶位上方的停留时间确定.

2.4 样品的真空退火处理

研究表明，溅射生长的MgO磁隧道结通常在350 ℃左右的温度退火一段时间后才能够让MgO势垒层晶化良好，使得磁隧道结性能提升. 另外，MgO/CoFeB/Ta体系在经过退火后，薄膜垂直磁各向异性增强[8]. 本研究在背景真空优于0.6×10-4Pa的真空退火炉中将3个样品进行无外磁场300 ℃退火处理，时间为1 h.

3 薄膜样品的测量

3.1 垂直磁化曲线测量

基于反常霍尔效应的测量方法可以得到垂直膜面的磁化曲线. 测量示意图见图1，霍尔电压VH满足：

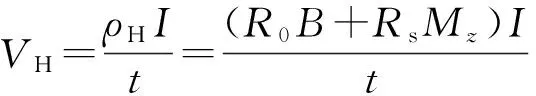
(6)其中，Rs称为反常霍尔系数，Mz为磁化强度，t为薄膜厚度，B为样品磁感应强度. 由于Rs≫R0，因而在较小的磁场下样品的VH-H图线，基本就对应着垂直磁场的磁滞回线Mz-H[6，9，10]. 严格上，可以通过大磁场的线性关系，将R0的影响完全扣除.

图1 垂直方向霍尔回线测量示意图

3.2 面内磁化曲线测量

VN∝zT(Q0B+4πQsMx),

(7)

其中，Q0为常规能斯特系数，Qs为反常能斯特系数，铁磁性材料中存在Qs≫Q0. 扣除线性项的影响，VN-H曲线代表的就是Mx-H曲线.

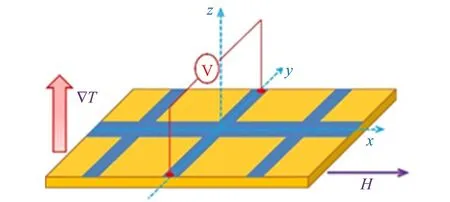
图2 面内方向磁化曲线测量示意图

4 测量结果分析与讨论

将3个样品均进行垂直方向霍尔回线的测量，设置磁场范围为±1.2×10-2T，步长为1×10-3T，结果见图3.

图3 样品的霍尔回线

由图3可以看出3个样品在垂直方向的磁化饱和场均较小，剩磁比接近100%，可基本判断薄膜具有垂直磁各向异性. 不过，完整的判据要求进一步结合面内磁化曲线. 通过面内和垂直方向的磁化曲线的对比，能真正确认薄膜为垂直易磁化还是面内各向异性，而两曲线所包围的面积对应垂直磁各向异性能的大小.

能斯特效应回线测量分别3个样品，设置磁场范围为±0.35 T(实验装置电磁铁所能达到的最大磁场)，步长为2.5×10-2T，得到VN-H测量曲线如图4所示.

图4 样品的反常能斯特电压测量曲线

由图可以看出，除CoFeB层厚度为1.0 nm的1#样品在外场大小为0.35 T时尚未出现趋于饱和的现象，其余2个样品均在外场较大的情况下出现了趋于饱和的现象. 显然，3个样品均已垂直磁化，磁化易轴垂直于膜面，难轴位于面内. 进一步，从能斯特曲线的饱和磁场可以估计CoFeB层厚度为1.1 nm和1.2 nm时，2个样品的有效垂直各向异性场约为0.15 T和0.05 T. CoFeB薄膜的垂直磁各向异性主要来自界面，作为一种界面效应，厚度越大，界面所占的比例就越小，效应自然相对的越小. 对比已有文献，T.Liu 等人测得Ta(5)/Co40Fe40B20(0.8-2)/MgO(2)/Ta(5)参量样品在经高真空300 ℃退火60 min后，其饱和磁化强度为1.65×106A/m3，根据其对于磁性薄膜的有效垂直磁各向异性常量与薄膜厚度的拟合研究，界面贡献参量Ks为1.7×10-3kg/s-2，体贡献参量Kv几乎为零[11]. 因而有效垂直磁各向异性场可由有效磁各向异性常量Keff的如下形式进行反推：

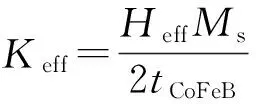
(8)

(9)

其中，Kv，Ks，t分别为磁性层体和界面对该体系薄膜各向异性的贡献参量与磁性层的厚度. 经反推计算，T.Liu等人的结果与本文所测得的有效垂直磁各向异性场的大小基本吻合.

5 结束语

利用反常霍尔效应与反常能斯特效应对“CoFeB/MgO”体系的有效垂直磁各向异性场进行了测量，实现了对于磁性薄膜的有效垂直磁各向异性场的全输运测量. 在实际应用方面，由于采用全输运测量法，不受磁矩大小与薄膜厚度的影响，对超薄膜尤其有利；另外，全输运测量法仅需要常规实验室具备的高精度电测量仪表，无须受制于磁测量相关的大型仪器设备，为薄膜磁各向异性表征提供了重要的补充手段.

致谢：本文在中国科学院物理研究所蔡建旺研究员的指导下完成，薄膜生长和磁输运测量全部在其实验室完成，其间亦得到邹吕宽博士和郑晓丽博士的相关指导.

[1] 吴少兵. CoFeB基垂直磁化膜的反常霍尔效应研究[D]. 武汉：华中科技大学,2013:47-49.

[2] 王芳，许小红. 振动样品磁强计在磁记录介质中的应用[J]. 信息记录材料,2005,5(2):55-59.

[4] 刘秋朝,袁淑娟,王磊,等. 铁磁/反铁磁多层膜中纵向和垂直交换偏置[J]. 扬州大学学报(自然科学版),2004,7(3):1-4.

[5] 朱艳燕. 磁性多层膜的垂直各向异性及巨磁电阻效应研究[D]. 上海：复旦大学,2013:15-16.

[6] 梁拥成,张英,郭万林,等. 反常霍尔效应理论的研究进展[J]. 物理,2007,36(5):385-390.

[7] 张俊杰. 反常霍尔效应和自旋霍尔效应的理论介绍和比较研究[D]. 金华：浙江师范大学,2009:8-19.

[8] 寇昕莉. 氧化镁磁隧道结磁电阻效应的研究进展[J]. 材料导报,2008,22(12):23-25.

[9] 周卓作, 杨晓非, 李震,等. 基于反常霍尔效应的薄膜磁滞回线测量系统的原理与设计[J]. 磁性材料及器件, 2011,42(2):43-45.

[10] 张静言. 基于反常霍尔效应的Co基自旋电子材料的研究[D]. 北京:北京科技大学,2015.

[11] Liu T, Cai J W, Sun L. Large enhanced perpendicular magnetic anisotropy in CoFeB/MgO system with the typical Ta buffer replaced by an Hf layer [J]. Aip Advances, 2012,2(3):413-421.Entire transport measurement of effective perpendicular magnetic anisotropy field of magnetic thin film

[责任编辑：郭 伟]

SHI Bi-zhao

(High School Affiliated to Renmin University of China, Beijing 100080, China)

Using magnetron sputtering method and a hall-bar shaped metal mask plate, CoFeB/MgO thin film samples were prepared, with CoFeB layer thickness of 1.0 nm, 1.1 nm, and 1.2 nm, respectively. The magnetic transport properties were measured by anomalous Nernst effect in vertical temperature gradient and anomalous Hall effect. The results were equivalent to the hysteresis loops in the conventional plane direction and the perpendicular direction, and thus the effective perpendicular anisotropy field was obtained, which was consonant with the data reported by

.

anomalous Hall effect; anomalous Nernst effect; magnetic thin films; effective perpendicular magnetic anisotropy field; entire transport measurement

2016-06-18

石弼钊(1999-)，男，北京人，中国人民大学附属中学学生.

学生园地

O484.43

A

1005-4642(2016)11-0032-04