白内障及屈光手术源性散光的计算方法汇总

赵海亮，张 健



·文献综述·

白内障及屈光手术源性散光的计算方法汇总

赵海亮1，张 健2

白内障摘除及人工晶状体植入术后影响视力的主要原因之一是术后散光。术后散光是术前散光和手术源性散光(surgically induced astigmatism，SIA)的矢量和。手术源性散光是一个矢量，既有大小又有方向。对手术源性散光进行计算分析，是进行白内障、屈光手术之前的必要步骤。本文就手术源性散光的计算方法进行综述。

白内障；角膜；散光；矢量分析

引用：赵海亮，张健.白内障及屈光手术源性散光的计算方法汇总.国际眼科杂志2016;16(12):2217-2220

0引言

随着白内障手术步入屈光手术时代，白内障患者和手术医师对术后视力要求越来越高，而影响术后裸眼视力的主要原因之一是术后散光。术后散光是术前散光和SIA的矢量和。SIA是由手术本身因素所造成的，包括术前、术后角膜散光及其轴向的改变。在没有达到最终散光之前，SIA是个可变量，即有时刻性。因手术前后散光不但有大小，而且有方向的变化，所以SIA也有大小和方向，即是个矢量。以前分析SIA往往采用简单法，即将散光度及其轴向分别进行分析，简单但准确性差。而矢量分析法等方法计算SIA的大小和方向，兼顾其两个特征，可准确反映手术造成术后的角膜散光情况。而且角膜屈光手术前后对于屈光度和散光度进行分析，可以了解屈光手术的手术疗效，这些分析需要应用上述矢量分析法。下面就手术源性散光的计算方法进行综述。

1手术源性散光的计算方法

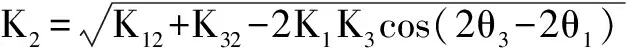
1.2极值法(polar values) 该方法由Naser[3]提出，公式为： KP=M×{sin2[(α+90)-Ω]-cos2[(α+90)-Ω]}其中M为净散光度(取两个轴位上散光度之差的绝对值)，α为较大屈光度所在的子午线，Ω和(Ω+90)表示术前更陡峭子午线的方向和其垂直方向，KP即极值，单位是屈光度，其中正极值表示顺规性散光，负极值表示逆规性散光。当Ω=90°时，KP(90)=M×(sin2α-cos2α),该公式计算了顺规性散光和逆规性散光部分的相互抵消。当Ω=135°时，KP(135)=M×[sin2(α-45)-cos2(α-45)]，该公式计算了投射到135°和45°轴位上散光部分的抵消。通过KP(90)和KP(135)可以描述任何散光，因此极值对于散光分析是一个普遍适用的方法。SIA用手术前后散光极值的差值来表示[4-6]。

本公式将复杂的散光矢量以一个简单的数值表示出来。此方法可以准确地计算出白内障手术引起的顺规或逆规的SIA。这使术者能够评估术前散光、切口类型、缝合技术和术后散光治疗等对SIA的影响，通过处理和选择手术方式，术者能够最小化SIA，也能帮助术者评价一系列不同的手术技术。矢量分析法描述整个散光的改变，包含散光的大小和方向；而极值法是一个简化的量，它在事先选定的方向上，通常是手术子午线的平面上定义散光的大小[7]。

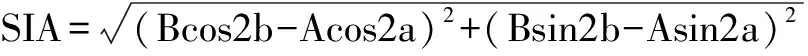
1.4 Cravy法(Cravy’s vector analysis)[9]该方法由Cravy于1979年提出，又称为三角法极值分析，SIA计算公式为：

Ks=M×θ°，

tanθ=△y/△x，

θ=arctan △y/△x，

Ks即SIA，M和θ分别代表SIA的大小和轴位，K1即术前净散光(取两个轴位上屈光度之差的绝对值)，K2即术后净散光(同上)，轴位分别是其较大屈光度所在的轴位，x1和y1即K1在坐标轴上分解后x和y的值，x2和y2即K2在坐标轴上分解后x和y的值，

△x=x2-x1，

△y=y2-y1，

该公式可以方便地计算成组患者的整体散光，其计算是伴随着手术切口愈合散光动态改变的顺序分析过程。同时该方法可预测正常和不正常的切口愈合，对通过拆除缝线确定SIA改变的值可能有帮助。

1.5 Naylor矢量分析法(Naylor′s vector analysis)[10]该方法由Naylor于1967年提出，又称为柱镜矢量分析法，SIA计算公式为：

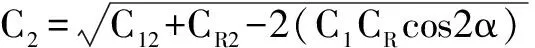
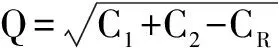
sin2β=(CR/C2)sin2α，

S2=SR-S1-Q，

其中C1、C2、CR分别表示术前散光、SIA、术后散光的大小，θ°、(θ+β)°、(θ+α)°分别表示术前散光、SIA、术后散光的轴位，S1、S2、SR分别表示其球镜大小，其中β值可以通过Naylor提供的表格查到。该方法给出因手术引起的球镜和柱镜改变的大小及柱镜即散光的方向，使SIA表达更为精确。

1.6 Thibos矢量分析法(Thibos′s vector analysis)[11-14]该方法由Thibos于1997年提出，该方法将屈光度(S，C×α)转换成函数成分(M，J0，J45)，M、J0、J45相当于在几何学上的三个正交的三维直角坐标(x、y、z)中x、y、z，该公式如下：

M=S+C/2，

J0=(-C/2)cos(2α)，

J45=(-C/2)sin(2α)，

其中S为球镜，C为柱镜，α为柱镜轴位，M为等效球镜值，J0为交叉柱镜在α=0°=180°上的数值，J45为交叉柱镜在α=45°上的数值，+J0为顺规性成分，-J0为逆规性成分，J45为斜向成分，B是估计屈光度异常引起视物模糊的指数，可以清楚地表示屈光手术前后未矫正屈光度导致视物模糊的程度。

应用Thibos提出的矢量分析法，可以有效地将手术所致屈光度和散光度的改变分解。每一个屈光度矢量都对应于三维直角坐标系上的唯一的一个点，矢量值为点至原点(0，0)的距离，反之亦然。而且这三个坐标是相互垂直的，意味着这三个变量是相互独立的。它将复杂的矢量计算简化成每个直角坐标上的简单加减，并且常用的统计学分析也适用于每个坐标轴。J0、J45、B在数学分析上是独立的，所以对角膜准分子激光手术前后的屈光度和散光度变化进行矢量转换后，可以直接加减、相互比较以及统计分析。而且，该方法将视光学理论与临床实践连接起来，可详细描述眼屈光异常和屈光手术疗效，使得全面达到视觉矫正，获得完美的视觉图像成为可能[13]。

1.7 Alpins矢量分析法(Alpins′s vector analysis)[15-21]该方法由Alpins于1993年提出，是基于传统的矢量分析来进行SIA分析的方法。它使用精确的直角坐标，提供正确的SIA的大小和角度，及不同的矢量来计算。设定K1、K2、K3和θ1、θ2、θ3分别为术前散光、目标散光、实际散光的大小和轴位，其中K1、K2、K3是净散光值，

X1=K1cos(2θ1)，

Y1=K1sin(2θ1)，

X2=K2cos(2θ2)，

Y2=K2sin(2θ2)，

X3=K3cos(2θ3)，

Y3=K3sin(2θ3)，

X1、X2、X3和Y1、Y2、Y3分别表示K1、K2、K3在X轴和Y轴坐标在360°内的矢量值。

X12=X2-X1，

Y12=Y2-Y1，

X13=X3-X1，

Y13=Y3-Y1，

X32=X2-X3，

Y32=Y2-Y3，

再进行以下计算：

θ12d=arctan(Y12)/(X12)，

θ13d=arctan(Y13)/(X13)，

θ32d=arctan(Y32)/(X32)，

K12=Y12/sin(θ12d)，

K13=Y13/sin(θ13d)，

K32=Y32/sin(θ32d)，

其中K12、K13、K32分别表示目标散光、SIA、矢量差值的大小，上述值如果为正值，则θ12d、θ13d、θ32d不需要转换；如果为负值，则需要180°转换。目标散光、SIA、矢量差值的方向分别为θ12、θ13、θ32，其计算方法如下：

θ12=θ12d/2，

θ13=θ13d/2，

θ32=θ32d/2

该方法提供了一个数学的精确评估手术的方法，可以比较不同眼和不同手术技术的差异，另外该方法提供的一些参数可以帮助术者获得想要达到的术后散光水平。通过定义一些特别的误差，可以获得更好的手术技术的使用和控制以及更精确的手术效果。

1.8 Holladay-Cravy-Koch法(Holladay-Cravy-Koch′s vector analysis)[22]由Holladay、Cravy、Koch于1992年提出，又称为Holladay十步计算法，手术矫正散光的量(surgically induced refractive correction，SIRC)计算方法：SIRC = PreRX- PostRX，EE + RX= RE，其中SIRC、PreRX、PostRX分别表示手术矫正散光的量、术前光学矫正值、术后光学矫正值，EE(the error of the eye)、RX(the optical correction)、RE(the residual error)分别表示眼屈光度、光学矫正的屈光度、残余屈光度。设球柱镜SC1和SC2，其中S1、C1、A1和S2、C2、A2分别表示SC1和SC2球镜值、柱镜值、柱镜轴位，SC3是目标球柱镜，它是SC1和SC2的矢量和，S3、C3、A3分别表示其球镜值、柱镜值、柱镜轴位。其中下面是十步法：

(1)调换SC1和SC2，使其柱镜有相同的正负号；

(2)SC1的A1值应该比A2值小；

(3)α=A2-A1；

(4)tan2β=C2sin2α/(C1+C2cos2α)；

(5)θ=(2β+180°)/2；

(6)SC=C1sin2θ+C2sin2(α-θ)；

(7)S3=S1+S2+SC；

(8)C3=C1+C2-2SC；

(9)A3=A1+θ；

(10)SC3可以转换为正或负的球柱镜形式SC4或者交叉柱镜形式SC5。

设SC1和SC2分别代表PreRX、-PostRX，计算SC3即可计算出SIRC。还可应用如下公式：SIRC = Kpost- Kpre，其中Kpost、Kpre分别表示术后和术前角膜曲率值，不过在现实中，角膜曲率常常测量不准确，而且折射的终点也不是很精确，故第一个公式较为常用。Holladay公式还可以计算眼镜的过矫，旋转角，相对于主子午线斜子午线上的屈光度，偶联比以及平均轴位等。

1.9三角几何法[23]采用三角几何法计算斜交叉圆柱镜方程，以确定手术前后圆柱镜的变化。设手术前后的柱镜分别为F1和F2，α为二者的夹角，C为手术产生的柱镜变化，AX为其轴线，S为手术引起的球镜变化，则

tanθ=(F2-F1+C)/(F2+F1+C)tanα，

AX= AXF1+ θ，S=(F1+F2-C)/2。

通过上述公式，根据术前和术后散光量和轴向，即可计算出手术源性散光量和轴向，在屈光手术后还可以计算每只眼手术效应轴和术前散光轴之间的夹角，与拟矫正的散光进行比较。

1.10美国角膜屈光手术矫正散光的标准化分析法[24- 25]由美国国家标准化组织Z80.1l工作组于2006年制定出的一套标准分析方法，用以评价屈光手术矫正散光的量(SIRC)等。设(Cpreop，Apreop)、(CIRC，AIRC)和(Cpostop，Apostop)分别表示术前散光、目标散光、术后散光的大小和轴位，

Xpreop= Cpreop×cos(2×Apreop)，

Ypreop= Cpreop×sin(2×Apreop)，

XIRC= CIRC×cos(2×Apreop)，

YIRC= CIRC×sin(2×Apreop)，

Xpostop= Cpostop×cos(2×Apostop)，

Ypostop= Cpostop×sin(2×Apostop)，

YSIRC=Ypreop-Ypostop，

XSIRC=Xpreop-Xpostop，

θ=0.5×arctan(YSIRC/XSIRC)，

SIRC表示手术矫正散光的量的大小，其轴位ASIRC如下：如果Y≥0且X>0，则ASIRC=θ；如果Y<0且X>0，则ASIRC=θ + 180°；如果X﹤0，则ASIRC=θ + 90°；如果X=0且Y>0，则ASIRC=45°；如果ASIRC=135°。对散光来说，一致的术语和分析方法对理解球柱镜屈光不正是必要的，该方法提供了一个综合的分析方法，可以用来评价角膜激光手术的散光矫正和其安全性、有效性，可以帮助分析不同机器的散光矫正效果。

1.11简单相减法(simple subtraction) 该方法仅在两个散光矢量轴位相同时应用，仅考虑其散光度大小，不考虑其轴位，该方法虽方便但欠准确，故应用较少。

2总结

计算手术源性散光对评估屈光手术效果、白内障手术的小切口及不同伤口愈合、缝线技术的效果及角膜移植缝线的拆除等非常重要。根据术源性散光矢量分析，可以指导白内障术者通过改善手术技巧来减小术后散光，可使术者评价手术因素对角膜散光的影响，从而使患者获得最佳的术后视力。屈光手术前后对于角膜屈光度和散光度进行矢量分析，可以全面评价手术前后的散光变化，并可评估眼屈光异常与屈光手术疗效，从而协助制定个体化准分子激光切削方案，获得更加完美的视觉图像。矢量分析犹如手术的航行舵手，它表明了未来手术的方向和过去手术的成功效果，散光矢量分析有效地比较了不同手术方法和术者散光手术的成功因素，通过使用手术矢量分析可以加强散光手术的计划性和收到更好的效果。在临床工作中，可以应用不同的散光矢量分析方法，通过比较其和实际效果来进一步指导临床实践，给予患者更佳的视力和视觉质量。

1张钧，王丽天，盛耀华. 白内障超声乳化术与手术性散光的关系. 中华眼视光学与视觉科学杂志 2002；4(2):123-124

2林英杰，梁先军，何锦贤，等. 同轴微切口白内障超声乳化术后角膜散光的临床观察. 国际眼科杂志 2013；13(7):1464-1466

3 Naeser K. Conversion of keratometer readings to polar values.JCataractRefractSurg1990;16(6):741-745

4 Naeser K, Hjortdal J. Bivariate analysis of surgically induced regular astigmatism. Mathematical analysis and graphical display.OphthalmicPhysiologicalOptics1999;19(1):50-61

5 Naeser K, Behrens JK, Naeser EV. Quantitative assessment of corneal astigmatic surgery: expanding the polar values concept.JCataractRefractSurg1994;20(2):162-168

6 Naeser K, Hjortdal J. Polar value analysis of refractive data.JCataractRefractSurg2001;27(1):86-94

7 Naeser K, Behrens JK. Correlation between polar values and vector analysis.JCataractRefractSurg1997;23(1):76-81

8 Jaffe NS, Clayman HM. The pathophysiology of corneal astigmatism after cataract extraction.TransAmAcadOphthalmolOtolaryngol1975;79(OP):615-630

9 Cravy TV. Calculation of the change in corneal astigmatism following cataract extraction.OphthalmicSurg1979;10(1):38-49

10 Naylor EJ. Astigmatic difference in refractive errors.BrJOphthalmol1968;52(5):422-425

11 Thibos LN, Horner D. Power vector analysis of the optical outcome of refractive surgery.JCataractRefractSurg2001;27(1):80-85

12 Thibos LN, Wheeler W, Horner D. Power vectors: an application of Fourier analysis to the description and statistical analysis of refractive error.OptomVisSci1997;74(6):367-37513 Thibos LN. The new visual optics.OptomVisSci1997;74(7):465-466

14 Diakonis VF, Yesilirmak N, Cabot F,etal. Comparison of surgically induced astigmatism between femtosecond laser and manual clear corneal incisions forcataract surgery.JCataractRefractSurg2015;41(10):2075-2080

15 Alpins NA. A new method of analyzing vectors for changes in astigmatism.JCataractRefractSurg1993;19(4):524-533

16 Alpins NA. New method of targeting vectors to treat astigmatism.JCataractRefractSurg1997;23(1):65-75

17 Alpins NA. Vector analysis of astigmatism changes by flattening, steepening, and torque.JCataractRefractSurg1997;23(10):1503-1514

18 Alpins NA. Astigmatism analysis by the Alpins method.JCataractRefractSurg2001;27(1):31-49

19 Alpins NA, Tabin GC, Adams LM,etal. Refractive versus corneal changes after photorefracive keratectomy for astigmatism.JRefractSurg1998;14(4):386-396

20 Krall EM, Arlt EM, Hohensinn M,etal. Vector analysis of astigmatism correction after toric intraocular lens implantation.JCataractRefractSurg2015;41(4):790-799

21 Lam DKT, Chow VWS, Ye C,etal. Comparative evaluation of aspheric toric intraocular lens implantation and limbal relaxing incisions in eyes with cataracts and≤ 3 dioptres of astigmatism.BrJOphthalmol2016;100(2):258-262

22 Holladay JT, Cravy TV, Koch DD. Calculating the surgically induced refractive change following ocular surgery.JCataractRefractSurg1992;18(5):429-443

23王铮，陈家祺，杨斌. 准分子激光角膜切削术治疗近视散光的临床分析.中华眼科杂志 1997；33(2)：132-135

24张杨，陈世豪，王勤美. LASIK术后的散光矢量分析. 眼科研究 2009；27(10)：893-897

25 Eydelman MB, Drum B, Holladay J,etal. Standardized analyses of correction of astigmatism by laser systems that reshape the cornea.JRefractSurg2006;22(1):81-95

Summary of calculation of surgically induced astigmatism in cataract and refractive surgery

Hai-Liang Zhao1, Jian Zhang2

1Department of Ophthalmology, Beijing Longfu Hospital, Beijing 100010, China;2Department of Ophthalmology, Xuanwu Hospital, Capital Medical University, Beijing 100053, China

Jian Zhang. Department of Ophthalmology, Xuanwu Hospital, Capital Medical University, Beijing 100053, China. drzhangjian@vip.163.com

•One of the main reasons affecting visual acuity after cataract extraction and intraocular lens implantation is postoperative astigmatism. The postoperative astigmatism is the vectorial sum of preoperative and surgically induced astigmatism. The surgically induced astigmatism is a vector which includes size and direction. And the analysis of surgically induced astigmatism is the necessary step before cataract and refractive surgery. This paper has summarized the method of calculation of surgically induced astigmatism.

cataract; cornea; astigmatism; vector analysis

赵海亮，男，硕士，住院医师，研究方向：白内障、角膜病。

张健，毕业于首都医科大学，硕士，主任医师，副教授，硕士研究生导师，研究方向：白内障、角膜病.drzhangjian@vip.163.com

2016-08-25

2016-11-14

1(100010)中国北京市隆福医院眼科；2(100053)中国北京市，首都医科大学宣武医院眼科

:Zhao HL, Zhang J.Summary of calculation of surgically induced astigmatism in cataract and refractive surgery.GuojiYankeZazhi(IntEyeSci) 2016;16(12):2217-2220

10.3980/j.issn.1672-5123.2016.12.11

Received：2016-08-25 Accepted：2016-11-14