从“—”到“||”，让符号生动起来

薛金梅

每每到七年级的时候，刚开始起步教学有理数时，都会遇到学不会，做不对的情形.对于某些学生来说，真的很难学，确切的说是很难理解.那么，是什么原因导致的呢？坦率地说，导致以上现象和问题的原因是十分复杂的.但我认为学生没有理解数学符号的意义是肯定的.短短的45分钟让学生记住一个计算步骤、掌握一个技巧或许可以，但是一算就乱、一写就错让我们师生双方都倍受打击.

现就七年级伊始教学的《绝对值和相反数》谈谈笔者的看法.

1.什么叫绝对值呀？学生不能理解.绝对值这个定义可不是能随意篡改的，我们就按照书上说的：“数轴上表示一个数的点与原点的距离叫做这个数的绝对值.”还要再多追问：如果不看数轴，我们可以怎么写出绝对值？学生会总结出一些适合他们自己记忆的方法.最多的是，纯数字部分（就是正数）不涉及正负.再问，为什么都是正的呢？学生们会七嘴八舌的说一些，最具合理性的就是，因为距离没有负的.绝对的数字，此乃歪解，但是很好记.

2.为什么绝对值的符号是“| |”？怎么能记得住.学生说这多容易呀.一写起来就不知道绝对值的概念飞到哪里去了.尤其是正负数混杂在一起的时候：有人写出|+9|=-9；也有求-3的绝对值，写成-|3|=3.我仔细研究后发现，前一种错误，是学生在写了一些负数的绝对值之后，以为，“| |”要把一个数写在符号里，就是把符号变一下，所以写|2.3|=2.3 没有问题，一上符号就不知所云了；第二种是完全没有理解| |的含义，内容听一半，自己脑补一半.

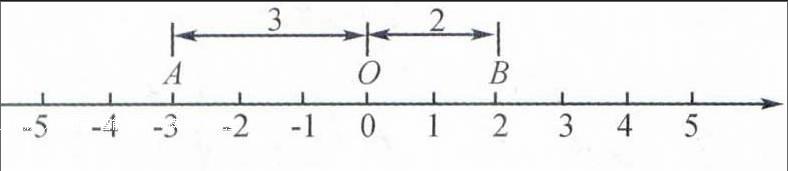
可怎么记住符号呢？我们在数轴上是这样演示的：

点A在原点O左侧且到原点O的距离为3个单位长度，点B在原点O右侧且到原点O的距离为2个单位长度.表示-3的点A与原点的距离是3，因此-3的绝对值是3；表示2的点B与原点的距离是2，因此2的绝对值是2；表示0的点O与原点的距离是0，因此0的绝对值是0.

你看，在数轴上OA间的距离我们用“| |”表示这段距离，所以我们选用| |表示绝对值符号.因为是距离，就绝没有负数的出现.

3.谈到|a|=-a（a < 0）， 学生就问了为什么是负的呀？我问a是什么数？一定是正数么？-a一定是负数么？说清楚a没有条件的情况下可以表示任何数，究其原因学生还不能很好地理解用字母表示数，以及相反数的符号.

那么，导致上述问题的根本原因是什么，数学教学应该注意什么呢？ 学生缺乏获取数学语言的能力，无法从数学符号中获得必要的数学信息，无法正确转化信息是根本原因.一方面，学生不能从数学符号中获得数学符号意义，也就失去了与教师对话的前提条件，就没有与教师互动的动机，只能被动地接受、记忆教师的观点；另一方面，学生不能从数学符号中获得数学符号意义，就无法向教师表达自己的理解，教师就无法准确把握学生的真实水平，容易造成数学教与学的脱节，导致学不会、做不对现象的发生.那么，是什么原因导致了学生缺乏数学符号意义获得能力呢？

1.数学教师忽视了数学知识与数学符号的差异，认为只要让学生记住了教师所讲的话语和教材中的符号，掌握了所练的数学题，就完成了教学任务.当数学教师将自己的经验性知识转换为陌生的、抽象的、枯燥的数学符号讲授给学生时，学生感受到的只是符号的写法和自己对符号意义的理解.这些言语意义只描述了知识的一个侧面或部分，如果学生不能进行认真的反思和体味，很难将数学符号的意义整合为有意义的数学形象.不理解成为必然，学生似懂非懂.

2. 数学教师忽视数学语言与自然语言的差异，不注重学生数学阅读能力的培养.很多教师认为数学书中的数学符号非常简单、数量有限，没有必要进行专门的数学语言教学，学生记住这几个简单的数学符号应该没有问题；也没有想过将文字语言、符号语言、图表语言三类在数学意义的表达上是各有特点和优势的.数学语言符号与自然语言符号有不同的意义表达方式.正是由于数学语言不同于自然语言，而数学教师又忽视数学语言的教学，使学生得不能正确理解数学语言，不能从数学符号中获得所需要的数学信息，成为很多学生学习数学的最大障碍.

3.数学教师忽视数学知识的结构性，使学生只掌握了一些孤立的知识点，没有形成系统的认知结构，不利于学生对数学知识的记忆和转换.数学符号一般有文字、符号、图表三种表征形式，而数学教师在讲课时往往只重视一种形式，导致了学生所学数学知识形式上的“孤立”，无法实现不同符号之间的相互转换；而教师却没有讲授这种转换的方法，更没有专门培养学生的这种符号结构意识和转换能力；最后，学生虽然能够当时听懂、记住孤立的数学知识和解题方法，但这些知识和方法更多是存储在短时记忆中，并没有通过精细加工程序进入到长时记忆中，所以学生会很快忘记所学的知识和所做过的题目.教师不仅没有指挥学生对所学知识进行精细加工，还给学生布置大量的作业，使得学生把主要精力都用到完成作业上，没有时间进行反思和自我总结.即使下次遇到的是同样的题目，学生常常只是保留一点模糊的印象，很难联想到更多的细节.因此，教师注重知识点的传授和掌握，忽视新知识点与原有知识点的联系，是导致做不对的一个重要原因.

4.数学教师忽视了数学符号意义的建构，将数学符号意义获得看作是数学符号意义记忆或理解，没有给学生建构数学符号意义提供充分的时间和机会.在当前的数学教学中，数学教师普遍重视数学知识的符号记忆，忽视数学知识的推导.记忆的数学符号随着时间的推移而很快消逝，只剩下一点模糊的记忆印迹.只有让学生养成知识推导的意识，掌握获取知识的方法，具备了获取知识的能力，才能在相应的情境下，激活模糊了的记忆印迹，在逻辑思维的帮助下恢复原有的知识.

因此，学习和使用新的数学符号时，教师有必要指导学生对数学符号做进一步的思考，对出现的错误进行深入的分析，确定错误的原因，找到正确的解法，提出改进的措施，强化学生的规范意识.数学学习中的困难一般是无法直接解决的，要全面分析导致困难的原因，采取各个击破的方法.用数学家G.波利亚的话说就是：解决困难的方法是迂回包抄.成功的数学符号教学起步，能帮助学生更好的学习数学，让数学符号生动起来，让学生爱动脑、爱思考吧，帮助他们学会提出问题并解决问题吧，让数学课堂也生动起来.