提升学生初中数学思维的两点思考
2016-12-03徐芹
徐芹
思维是认知的核心!我们的数学教学应该关注学生的思维发展,在教学过程中如何有效提升学生的数学思维呢?本文从新授课,习题课两个方面进行分析.
一、新授课学生数学思维的培养与提升
新授课如何培养学生的数学思维呢?
新课程在学习模式上也有改革的要求,强调学生是学习的主体,数学思维也并非是灌输的,有序地发展学生的数学思维需要我们教师主导性作用的发挥.
首先,在每一节新授课之前,我们教师应该结合学生的学情和所教内容的实际情况,进行合理的分析,继而拟定活动单或导学案.活动单、导学案是一份学习方案,凸显导学功能,是链接三维教学目标和学习内容、学生已有知识和待学知识之间的桥梁,也是学生进行学习,提升自己知识、发展能力的一个重要指导.在活动单中应有科学合理的问题设计,设计的问题应立足教材,来源于生活,同时又具有较强的数学思维继发性.
教材是什么?
教材是学生学习内容的例子!是经过课程专家进行挑选的,符合学生学龄特征和思维发展要求的例子,承载着数学知识、思维和方法,是我们与学生一起学习初中数学的最为主要的资源.不仅仅如此,如果站在应试的角度看教材,它也是中考命题专家手头最为重要的“题源”.我们的问题设计应该对教材进行深度的挖掘.
例如,笔者在和学生一起学习“无理数”这个概念时,可以进行如下的设计,通过一个情境引出多个问题,引导学生的思维不断深化.
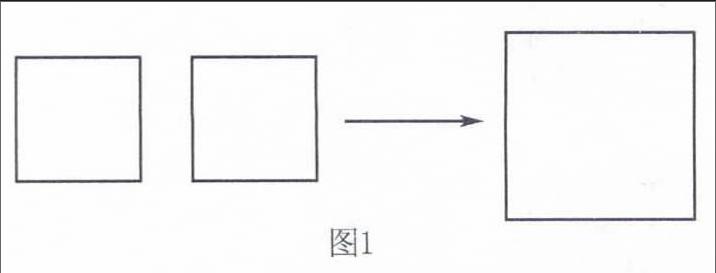
情境(PPT投影):现在有两张完全相同的,边长为1正方形纸片,如果将这两个正方形剪开,如图1所示拼接出一个大正方形,请思考如下几个问题.
(1)求拼接得到的那个大的正方形面积;
(2)求拼接得到的大的正方形的边长.
设计意图:从问题的设计来看,第一个问题的起点相对较低,学生很快可以发现这样的拼接面积不变,所以大的正方形面积为2,但是很多学生对于其边长的思考容易卡壳,怎么办?可以进一步追问.
追问1:边长大约是多少?
追问2:可以用分数来表示么?
设计意图:通过追问让学生的思维的台阶降低,笔者在教学中发现,追问后学生会跟着问题的节奏思考,最终发现有理数在表示大的正方形边长时存在着障碍,怎么办?在不能解决时,新的问题随之而来,“用什么数来表示呢?”探究欲望和问题意识都被有效激发.这一过程中学生的思维能力得到有效的发展.
二、习题课学生数学思维的培养与提升
1.分析学生解题出错的错因并提前预防
习题教学是我们不得不重视的课型,不过我们的习题教学应该如何上呢?笔者认为除了要教给学生正确的解决数学习题的方法外,还应该正视学生在解题过程中出现的错误,和学生一起分析出现解题错误的成因,一起总结解决问题的方法,实现从错误走向正确.这样的学生的思维会得到正向的引导.
初中数学学生更多的学习是代数,而且学生有小学的基础,但是错误还是时常发生,例如,“数与式”处理上学生就常常容易犯错,具体的易错点与原因分析如下.
错因1:学生对概念理解上的偏差导致了错误,如在实数的范围内,涉及到若干个概念,正数和负数,无理数与有理数,平方根和算术平方根等等,理解上的偏差势必导致在应用和描述上出现问题.
错因2:学生在实数范围内进行数与式的计算时,由于不能非常熟练地掌握和运用基本技能,导致在进行变形与计算时出现了较为明显的错误.
错因3:学生在学习过程中由于对各个代数式的认识存在着较为模糊的现象,导致在判断与应用上出现错误.
错因4:学生间存在着较为明显的个体差异,导致有部分学生的观察、分析与总结的能力出现部分缺失,综合能力偏弱,面对一些综合性的习题时,解决存有困难.
例如,16的算术平方根是多少?
很多同学初次遇到这个问题时会错误地认为结果是4.为什么会出现这样的错误结果呢?笔者和学生交流后发现,学生出错的主要原因在于对数学概念的理解出现偏差,对根号的意义和符号语言缺乏深入的理解,如果将符号转化为语言,那么这个数学问题等价于:求16的算术平方根的算术平方根,这里有开方开2次,最终的正确结果应该是2.这就是典型的学生对代数式的理解存在偏差导致了解题出现错误.
那么,这类问题如何引导学生进行预防呢?
首先,应该引导学生深化对概念的理解与研究,注意防止知识陷阱.
其次,要加强运算的熟练性、准确性,同时给学生提供更多训练的平台,切实提升学生解决数学问题的技巧性.
2.拓展训练,促进思维与知识“框架化”发展
由于学生的思维能力还不够成熟,所以对于数学知识的学习和方法的积累很多时候不可能一步到位,只有通过多个角度的训练才能得到内化和发展,笔者认为为了有效促进学生思维和知识的框架化发展,我们的拓展训练不可缺失,问题设计应具有综合性,同时还应该设计变式训练.
例如,“三角形全等”的习题课中,笔者有如下的问题设计.
例1 在△ABC中,AB=AC,MN是过A点的直线,已知BD⊥MN于D,CE⊥MN于E,根据所学内容思考如下2个问题:
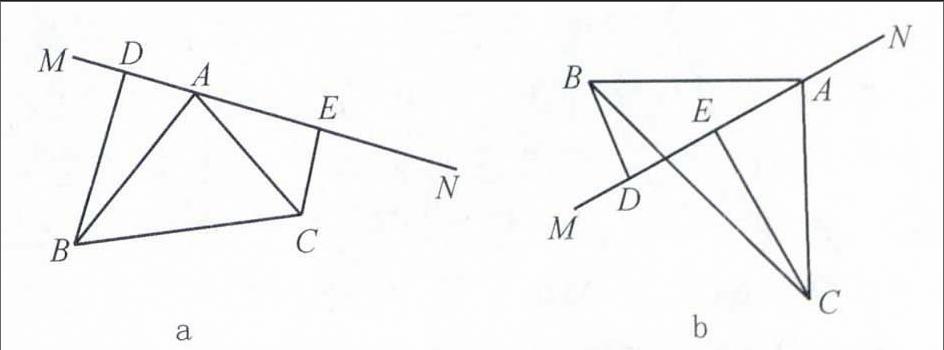
问题1 若B、C分别位于直线MN的同侧(如图a所示),且AD=CE,求证:AB⊥AC;
问题2 若B、C分别位于直线MN的两侧(如图b所示),且AD=CE,试分析AB与AC是否垂直?
学生在解决完这个例题后,为了帮助学生提炼解决问题的办法,促进知识框架和思维框架的建立,进行如下的变式.
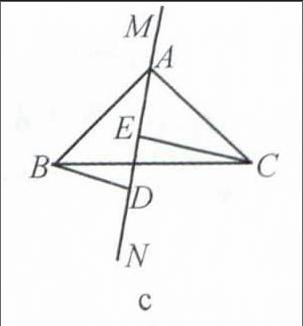
变式 在△ABC中,∠BAC=90°,AB=AC,MN为一条过C点的直线,已知BD⊥MN于D,CE⊥MN于E,现在绕A点将直线MN旋转到图c所示的位置,请猜想DE、BD、CE之间可能存在的等量关系,写出关系式,并试着证明你的猜想.
设计意图 通过这样的综合性问题设计和变式处理,学生的框架逐步地趋于严谨、精细,思维能力和学习情感也在解决问题的过程中逐步地提升.
