自膨胀支架几何参数对服役影响的有限元分析*
2016-12-03张会娟王伟强
张会娟,王伟强,齐 民
(大连理工大学 材料科学与工程学院,辽宁 大连 116024)
自膨胀支架几何参数对服役影响的有限元分析*
张会娟,王伟强,齐 民
(大连理工大学 材料科学与工程学院,辽宁 大连 116024)
自膨胀式血管支架的成功服役主要受制作材料和支架几何参数的影响。大波段Z型支架由于其实验室制作工艺简单、便于测试、有好的临床适用性,广泛用于实验分析和有限元分析中。本文主要运用有限元法,分析了自膨式Z型支架几何参数对其力学服役的影响。通过参数化模拟对照,发现增加顶端圆弧半径、增加支撑体长度、增加圆周V型个数均会减小支架径向抗力。但是支架超出血管的尺寸对径向抗力影响不大。对支架脉动受载及易疲劳区位置进行分析表明,支架在服役时,舒张压和收缩压下平均应变和交变应变分布不一致,最先发生疲劳的位置是支架顶端圆弧内侧,受力状态是压缩。
镍钛合金;血管支架;有限元;参数化;疲劳
0 引 言
超弹性自膨式镍钛合金支架可以在发生大变形后恢复,在血管疾病的治疗上有很大的优势,特别适用于服役时出现大变形的部位,如膝盖[1],颈动脉[2],股动脉[3],以及表层动脉等外周血管部位。
自膨式支架的成功服役受很多因素的影响,如支架几何[4-5],制作材料[6],输送系统以及支架与血管接触相互作用等[7-8]。对于大血管来说,Z型支架是应用很广泛的一种。由于实验室制作工艺简单,尺寸较大,测试容易,Z型支架被广泛用于有限元分析和实验分析中。Duerig等通过理论分析得出了Z型支架受力变形与支架几何参数的关系[9]。但具体的参数化分析多是针对激光切割类支架,对大血管金属丝定型支架的参数化分析还很少。本文主要是针对镍钛合金Z型大血管支架,通过控制支架几何参数,研究其对受力的影响,并将结果和理论分析进行对比。同时也对支架的脉动受载进行了分析,为今后支架设计和选择提供借鉴。
1 材料和方法
1.1 材料属性和单元
和一般金属材料不同,镍钛合金的超弹性是一种通过相变实现的伪弹性。材料初始为奥氏体态,施加外力(拉伸或压缩)时,首先发生弹性变形。当变形到一定程度时,材料产生应力诱发马氏体相变,由奥氏体态变为马氏体态。对应地材料应力应变曲线上会产生加载平台,亦即在外力增加很少的情况下,材料产生大的变形,直至完全相变为马氏体。之后,若继续施加外力,应力应变曲线上平台期结束,材料进入马氏体弹性变形阶段。此时外力逐步撤除时,马氏体先弹性恢复,随后逆相变,由马氏体转变为奥氏体,对应地材料应力应变曲线出现卸载平台(下平台)。再继续撤力,奥氏体弹性变形恢复,实现材料的伪弹性变形过程。
本模拟是基于ABAQUS6.12软件,表1列出了模拟中支架的材料参数[10]。在软件实现上,主要是运用ABAQUS内置的镍钛合金超弹性本构模型(C3D8R)。
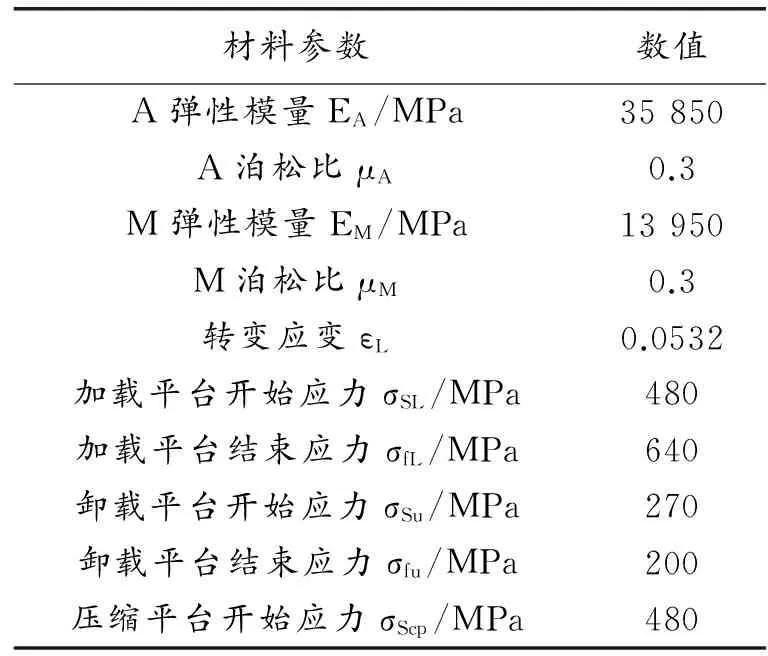
表1 镍钛合金材料参数
对于压缩支架的工具,模型采用surface单元中SFM3D4R。血管建模采用线弹性本构(C3D8H)。材料属性[11]如表2所示。

表2 血管材料参数
1.2 模拟控制过程
图1表明了支架建模的几何外形。实际应用中,支架由一系列特定形状的金属环连接而成。对于大动脉血管,支架一般由金属丝热处理定型,最后通过和覆膜的缝合连接而成。
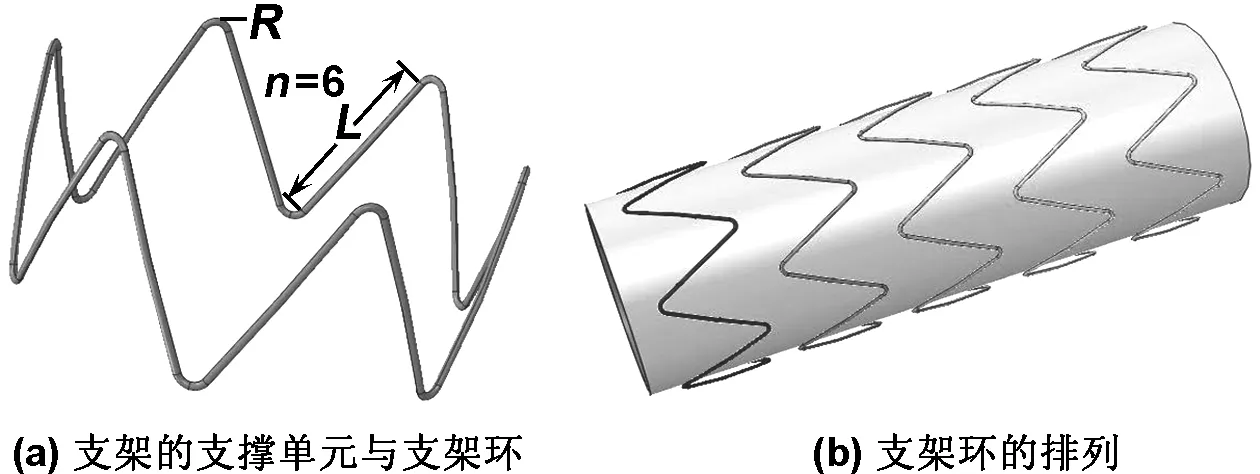
图1 支架的支撑单元与支架环和支架环的排列
Fig 1 Stent supporting unit and the stentring and alignment of stent rings
支架在置入体内的过程中,会经历一系列的变形。所以模拟分为以下控制过程:(1) 支架从原始直径压缩到目标尺寸(22Fr);(2) 支架释放与血管接触;(3) 支架脉动受载。
1.3 建模方法
本模拟运用ABAQUS/standard模块求解分析。由于分析重点是支架的受力情况,血管和压握工具均简化为圆柱。模拟运用柱坐标控制,设置Z方向为支架长轴方向。由于支架、血管和压缩工具均环向对称,为节省计算资源,均选取部分进行建模,在截取面上设置圆周对称边界。同时,为避免支架在Z方向出现大的刚性位移导致计算不收敛,在支架端部点设置Z向位移为0。
本模拟是探究支架几何参数对服役的影响,考虑以下几个参数(参见图1(a)):支撑体连接弧半径R,支撑体长L,圆周V型支撑体个数n,支架超出血管尺寸O(用支架和血管的直径比dstent∶dartery表示)。具体参数化模拟设置,如表3所示。

表3 模拟参数设置
支架详细植入过程控制如下:第一步,压握过程。支架在压缩鞘作用下被压在导管内。压缩鞘的运动通过位移控制,在柱坐标下,设置径向位移边界。支架和压缩鞘的接触运用主从接触面算法,摩擦系数设为0。第二步,植入过程。支架从输送器释放与血管接触。支架膨胀由内部储存的变形能驱动,撤销压缩鞘后,支架自发膨胀。当膨胀接近血管尺寸时撤销压缩鞘与支架的接触,达到稳定释放。接触算法同压缩步,同时设置支架和血管之间摩擦系数为0.2。血管长轴端面设置U2=U3=0,径向U1保持自由。第三步,脉动服役。此过程支架在血管收缩压和舒张压下随血管运动。由于正常血管在脉动时随心脏收缩和扩张下脉动幅度一般为5%[12]左右,模拟运用位移控制,设置支架的脉动直径变化为植入血管直径的±2.5%。
1.4 不同服役阶段支架力学性能的表征
血管支架在整个服役过程中,不同阶段受力不同,相应关注的重点也不同。在压缩进入输送导管的预装过程,关注力学参量主要是支架的径向抗力和最大主应变[9]。其中径向抗力指标在本文中用单个支架环在径向对压缩鞘的反作用力表示。在置入后,主要关注的是支架长期安全性,本文用支架脉动时的平均应变和交变应变来表示。
2 模拟结果
2.1 连接弧半径对支架压握过程的影响
从图2(a)可以看出,一定范围内,弧半径越大,压缩到相同直径,支架的径向抗力越小,压缩到最小半径时最大主应变越小。同时发现在连接弧半径达到1.4R时,径向抗力出现突增(图2(a))。这是由于发生了自接触,之后压缩支架需要更大的力,同时应变值也增加。
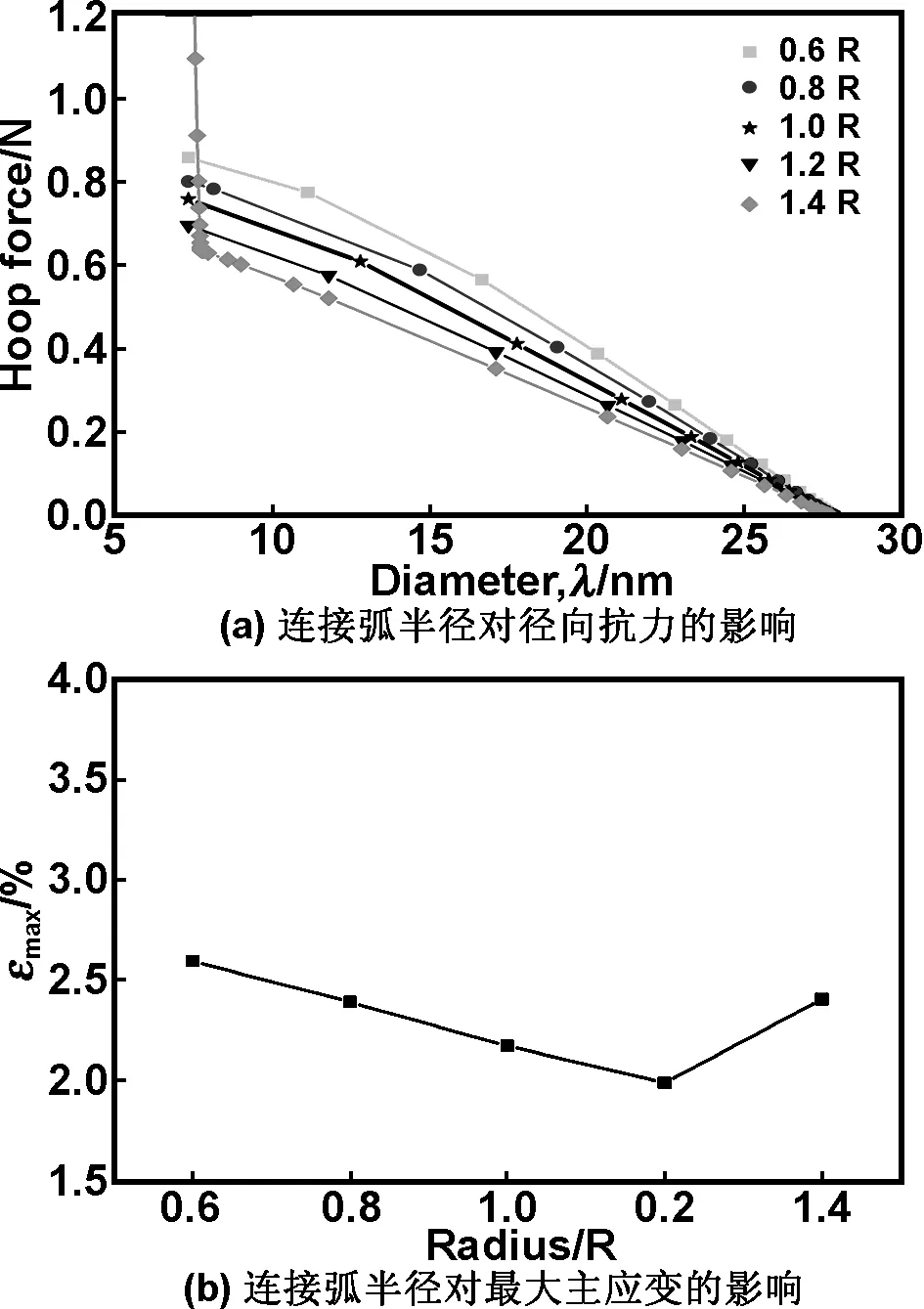
图2 连接弧半径对径向抗力的影响和对最大主应变的影响
Fig 2 The effect of crown radiuson radial resistance and on maximum principal strain
2.2 支撑体长度对支架压握过程的影响
从图3可以看出,随着支撑体长度的增加,支架的径向抗力减小,越容易被压缩,在压缩到最小直径时,主应变越小。
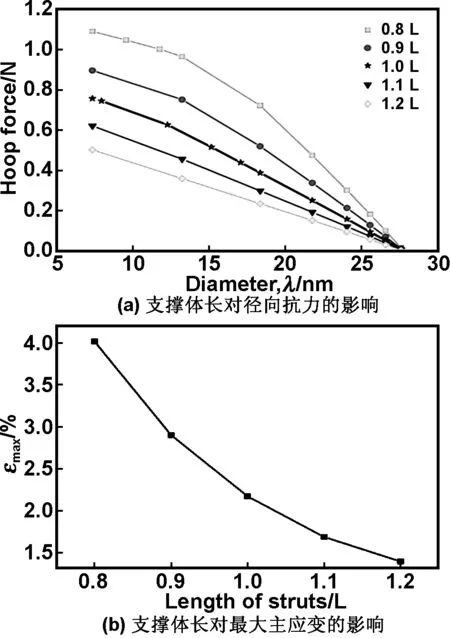
图3 支撑体长对径向抗力的影响和对最大主应变的影响
Fig 3 The effect of length of struts on radial resistance and on maximum principal strain
2.3 圆周方向V型支撑体数目对支架压握过程的影响
从图4可以看出,随着圆周方向V型支撑体数目增加,支架径向抗力变小。但在数目增加到10时,压缩接近输送器直径时出现了径向抗力突增的现象。
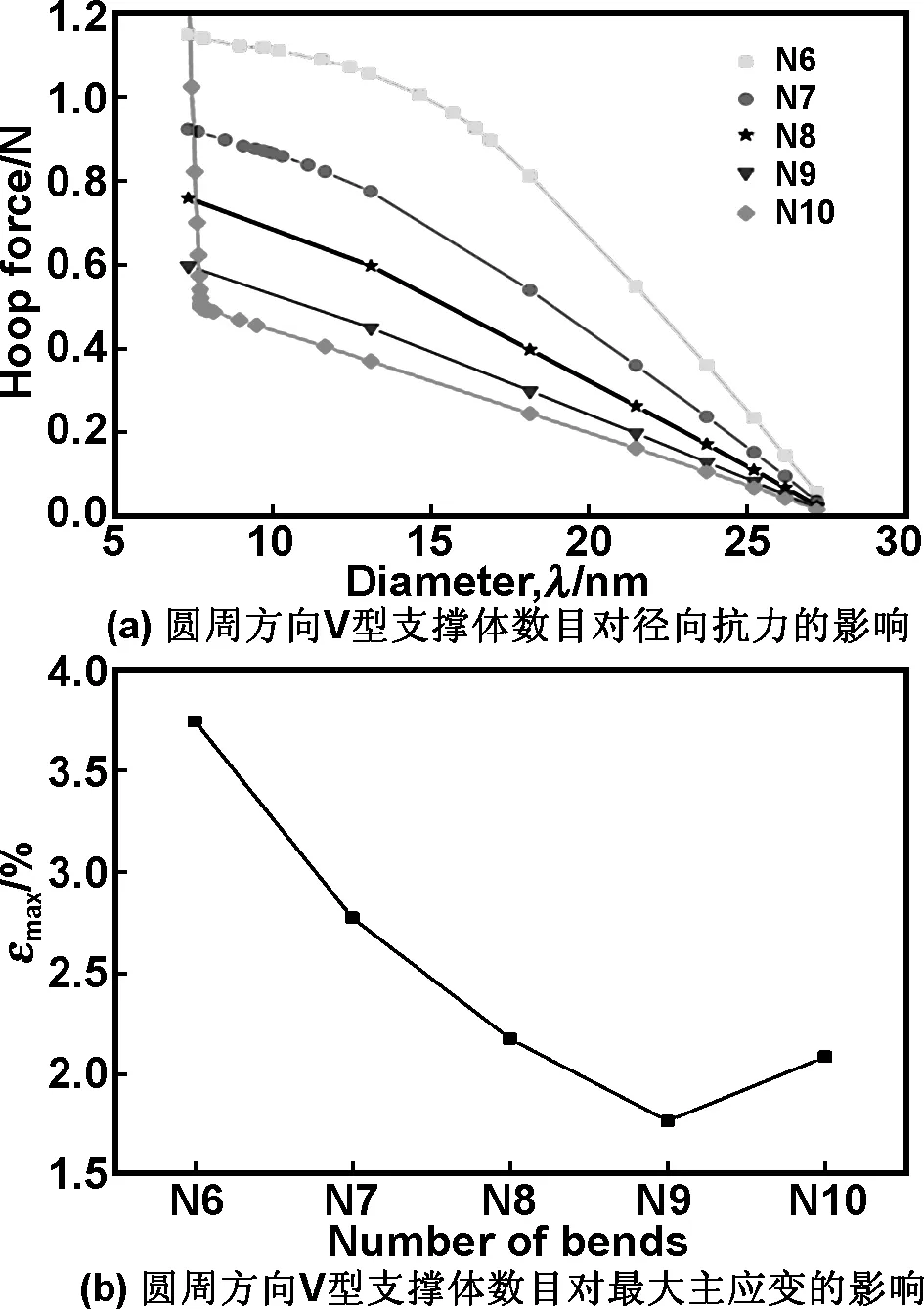
图4 圆周方向V型支撑体数目对径向抗力的影响和对最大主应变的影响
Fig 4 The effect of thenumber of V-shapedsupporting unit along circumference on radial resistance and on maximum principal strain
这是由于V型数目增加时,支架的径向轮廓增加,压缩到相同尺寸,相邻支撑体之间发生自接触,难以继续压缩,导致径向抗力突增(图4(a))。在压缩主应变上,随着V型数目增加主应变减小。同样在数目为10时由于强制压缩,最大主应变也出现了突增(图4(b))。
2.4 支架超出血管尺寸对支架压握过程的影响
从图5可以看出,支架超出血管尺寸对支架的径向抗力影响不明显。随着匹配过盈量的增加,支架径向抗力出现小的增加趋势。同时,压缩到最小直径时的最大主应变也小幅度增加。

图5 支架超出血管直径对径向抗力的影响和对最大主应变的影响
Fig 5 The effect of stent oversizing on radial resistance and on maximum principal strain
2.5 支架脉动受载时受力情况
针对支架脉动服役时的受力情况,本文运用python脚本对模拟结果进行了后处理,提取了支架在血管收缩压和舒张压结束状态的最大主应变数值,并计算了两个状态下的平均应变和交变应变。由于所有对照组支架的应变云图分布均相似,本文给出了对照组3中N=6支架的分析结果,见图6。从中可看出,平均应变和交变应变的最大值区域分布不一致。平均应变最大值区域位于支架弯曲圆弧外侧,而交变应变最大值区域位于连接弧顶端内侧。分析支架对应的应力云图发现圆弧内侧应力状态是受压。
3 讨 论
3.1 支架几何参数对其受力的影响
Duerig等[9]在对激光切割Z型支架几何参数对其受力影响的研究中,给出了支架V型支撑体数目、支撑体长度,支撑体横截面宽度和厚度对其径向刚度的影响,相关表达式如下
K∝Ew3t/nL3
(1)
其中,K是径向刚度,n是环向V型支撑体的数目,L是支撑体的长度,E是材料弹性模量,w是支撑体的宽度,t是支撑体的厚度。对应支架受力,表达式如下
F=PDL/2
(2)
其中,P是血压,D是血管直径,L是支架支撑体的长。经过一系列推导可以得出,在相同的直径变化下,支架径向受力和几何参数的影响关系如下
F∝Ew3t/n L2
(3)
从式(3)可知,对于此种激光切割型支架,环向V型支撑体越多,支撑体越长,其径向抗力越小,这和本文中以金属丝制成的Z型支架几何参数变化与对受力影响的规律一致(见图3、4结果)。
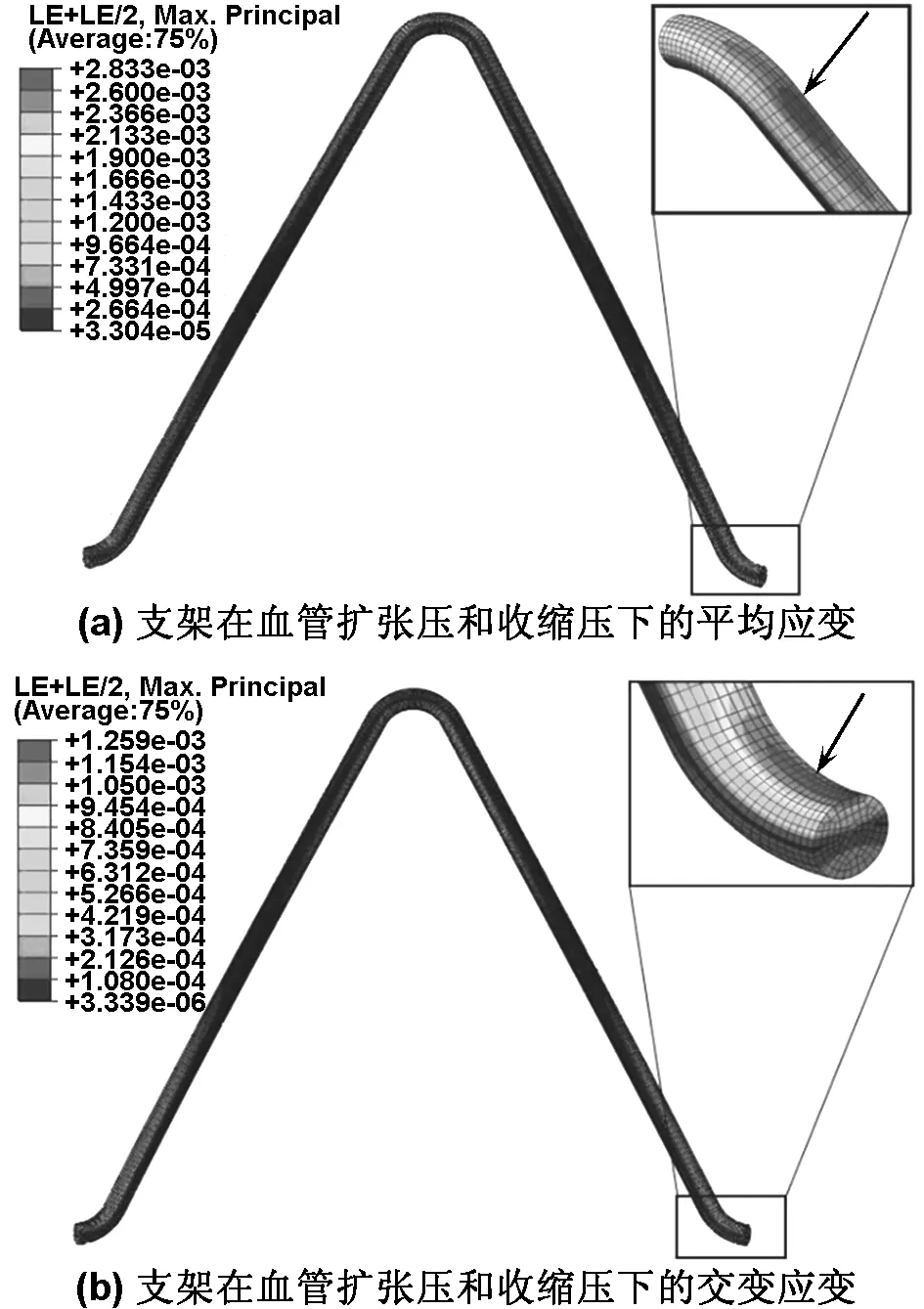
图6 支架在血管扩张压和收缩压下的平均应变和交变应变
Fig 6 The mean strain and alternating strain of stent on diastole and systole pressure
Hsiao和Pike的研究[6,13]均指出,连接圆弧对支架整体力学影响很大,但并没有明确指出其影响规律,同时,式(3)中也没能反映出Z型支架顶端连接弧和支架超出血管尺寸的影响。通过本次模拟发现,支架连接弧半径越大,其径向抗力越小。但径向抗力并非越大越好,径向抗力变大,即连接弧半径变小,会使支架V型结构定型困难,且植入后和血管接触形成接触应力也较大,易对血管造成损伤;径向抗力太小,不能对血管形成很好的支撑,不利于形成新的血流通道。同时,模拟结果表明,连接弧半径增加会导致支架压缩时自接触的提前发生,亦即会影响其径向可收缩尺寸,而支架的径向可收缩尺寸则限制了输送器的最小轮廓尺寸及其在血管中的可通过性。针对支架的过盈尺寸参量,模拟发现,超出血管的尺寸对支架径向抗力没有明显影响,但不可忽略的是,过盈尺寸的加大会增加支架服役时覆膜的褶皱程度,而这将会对覆膜的贴壁性造成影响。
3.2 支架易疲劳区域分析
已有研究[12]指出,镍钛合金的疲劳是应变控制型,且交变应变是支架疲劳的主要影响因素。James等[14]对镍钛合金丝的弯曲压缩变形进行了分析。其结果指出,对于存在预弯曲定型的镍钛合金丝,当经历大幅度压缩变形时,圆弧内侧会产生大的压应力和压应变,导致此处表面组织的粗糙化并产生微裂纹,即形成压缩损伤。此种微裂纹在合金丝压缩并释放时,会向前扩展。支架的脉动服役其实质就是V型结构的压缩与张开。由此推断出,材料的疲劳循环会促使圆弧内侧压缩区裂纹的扩展。对于本文的Z型支架环,模拟得出支架的交变应变较大值区域也位于合金丝V型结构圆弧内侧,亦即对于此种结构镍钛合金丝的变形,模拟分析和上述研究得出的疲劳脆弱区的推断是一致的。
另有学者指出[15],当镍钛合金材料的平均应变小于1.5%或2%时,支架的疲劳极限即发生疲劳失效的临界交变应变是0.4%;当平均应变增加到1.5%或是2%时,材料耐疲劳性会增加,即临界交变应变值应大于0.4%。此现象主要与材料应力诱发马氏体相变有关。应变的增加会诱发材料发生相变,缓解了变形时的应力集中,增加了材料的耐疲劳性。因此在分析支架的疲劳时,也需进行平均应变的分析。本文模拟的各参数Z型支架,在脉动服役时的平均应变最大值均小于1.5%,而对应的交变应变云图中,其交变应变最大值均低于0.4%,因此在不考虑其它因素的影响下,此参数范围内的支架均是安全的。
4 结 论
自膨胀镍钛合金支架除却材料的影响,其设计对服役也有着举足轻重的作用。本文通过有限元法,研究了支架关键几何参数对受力的影响,分析了支架置入后脉动受载时的应变分布情况,最终得出以下结论:
(1) 支架支撑体长度增加,圆周V型支撑体个数增加均使其径向抗力减小;顶端圆弧半径对径向抗力有很大影响,圆弧半径增加使径向抗力减小;支架超出血管的尺寸对径向抗力影响不大。
(2) 支架的易疲劳区主要受力状态是受压,位于Z型支架弯曲圆弧的内侧。
[1] Jaff M R. The nature of SFA disease[J]. Endovascular Today, 2004, 4: 13-15.
[2] Auricchio F, Conti M, De Beule M, et al. Carotid artery stenting simulation: from patient-specific images to finite element analysis[J]. Medical engineering & physics, 2011, 33(3): 281-289.
[3] Petrini L, Wu W, Dordoni E, et al. Fatigue behavior characterization of nitinol for peripheral stents[J]. Function Materials Letters, 2012, 5(1): 1-4.
[4] Hsiao H M, Wu L W, Yin M T, et al. Quintupling fatigue resistance of intravascular stents via a simple design concept[J]. Computational Materials Science, 2014, 86(15):57-63.
[5] Gao Z Y, Liang D K, Qi M et al. The longitudinal flexibility analysis of nitinol self-expanding stent[J]. Journal of Function Materials, 2007,38(1):113-114.
[6] Liu X P, Wang Y N, Yang D Z, et al. The effect of ageing treatment on shape-setting and superelasticity of a nitinol stent[J]. Materials Characterization, 2008, 59(4):402-406.
[7] Azaouzi M, Makradi A, Belouettar S. Deployment of a self-expanding stent inside an artery: a finite element analysis[J]. Materials and Design, 2012, 41: 410-420.
[8] Liang D K, Yang D Z, Qi M, et al. The finite element analysis of superelastic nitinol intravascular stent[J]. Journal of Function Materials,2005, 36(3):471-476.
[9] Duerig T W, Tolomeo D E, Wholey M. An overview of superelastic stent design[J]. Minimally Invasive Therapy & Allied Technologies, 2000, 9(3/4):235-246.
[10] De Bock S, Iannaccone F, De Santis G, et al. Virtual evaluation of stent graft deployment: a validated modeling and simulation study[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2012, 13: 129-139.
[11] Kleinstreuer C, Li Z, Basciano C A, et al. Computational mechanics of nitinol stent grafts[J]. Journal of Biomechanics, 2008, 41(11):2370-2378.
[12] Duerig T, Pelton A, Stockel D. An overview of nitinol medical applications[J]. Materials Science and Engineering: A, 1999, 273-275(15): 149-160.
[13] Pike K, Berg B, Adler P. Development of the Z specimen for tensile-tensile, tensile-compression, compression-compression wire testing[J]. Journal of Materials Engineering and Performance, 2011, 20(4):835-837.
[14] James B, Murray S, Saint S. Fracture characterization in nitinol[C]//: Proceedings of the International Conference on Shape Memory and Superelastic Technologies, 2004, 321-329.
[15] Fatigue testing of diamond-shaped specimens[C]//: Proceedings of the International Conference on Shape Memory and Superelastic Technologies, 2004, 293-302.
Finite element analysis of the effect of self-expansion stent geometry on its performance
ZHANG Huijuan, WANG Weiqiang, QI Min
(School of Materials Science and Engineering, Dalian University of Technology, Dalian 116024, China)
The successful performance of self-expansion stent, in terms of stent design, is mainly influenced by the used material and geometric parameters of the stent. Big band Z-strutstent, for the reasons thatit has simpleproduction process, easy to test, and has a good clinical applicability, is widely used in experimental analysis and finite element analysis. In this paper the finite element method was used to analyze the influenceofthegeometric parameters of self-expanding stentonits mechanical service. Through parametric simulation control, it was found that increasing the crown radius, the length of the support, and the number of V-shaped strut alongcircumference will reduce the radialresistance. But stent oversizing has little effect on radial stiffness.Withpython script processing, the state of stress and strain distribution was analyzed, thelocation of fatigue zone and the stress and strain state of this zone were analyzed and discussed as well.Itwasdiscovered that when the stent moved with diastole and systole pressure, the mean strain and alternating strain distribution areinconsistentwith each other, and the position of the first occurrence of fatigue exist insideof the crown where stress state is compressed.
nitinol; stent; FEA; parameterization; fatigue
1001-9731(2016)04-04094-05
国家自然科学基金资助项目(51371042);中央高校基本科研业务费专项资金资助项目(DUT13JB06)
2015-03-10
2015-05-25 通讯作者:王伟强,E-mail: wangwq@dlut.edu.cn,齐 民
张会娟 (1990-),女,郑州人,在读硕士,师承齐民教授,从事血管支架研究。
TB381
A
10.3969/j.issn.1001-9731.2016.04.019
