海杂波特性认知研究进展与展望

2016-12-03董云龙刘宁波王国庆

雷达学报 2016年5期

关键词：杂波分量特性

丁昊董云龙刘宁波王国庆关键

(海军航空工程学院电子信息工程系烟台 264001)

海杂波特性认知研究进展与展望

丁昊*董云龙刘宁波王国庆关键*

(海军航空工程学院电子信息工程系烟台 264001)

海杂波是影响海用雷达目标探测性能的主要制约因素之一，其物理机理复杂，影响因素众多，且非高斯、非平稳特性显著，因此海杂波特性认知研究是一项极其复杂的系统工程。该文从数据层海杂波特性认知出发，围绕目标检测算法所关注的海杂波幅度分布特性、谱特性、相关性及非平稳与非线性特性，回顾和总结了海杂波特性认知研究进展，梳理了主要研究结论。在此基础上，从海杂波影响因素的深化分析、海杂波精细化建模与检测器需求的博弈、海杂波与目标差异特性认知等4个方面展望了有待于进一步探索的问题。

海杂波；特性认知；非高斯；非平稳；精细化建模；目标检测

1 引言

无论在军事方面还是民用方面，对海雷达快速可靠地发现海上目标都具有越来越重要的意义。然而，雷达面临的工作环境复杂多变，其接收的回波信号中除了感兴趣的目标回波外，还包含噪声、干扰、海杂波等。在上述因素中，由于海杂波功率水平较高，且非高斯、非平稳特性显著，再加之其影响因素的复杂性和多变性[1]，导致海杂波成为影响探测性能的主要制约因素之一。为此，从目标探测的需求出发，开展海杂波特性认知研究，掌握海杂波变化趋势并建立海杂波模型，是有效改进和创新海杂波抑制算法和目标检测算法、削弱海杂波不利影响、实现探测性能提升的基本前提和基础[2]。

目前，国内外围绕海杂波特性认知问题已开展了大量研究，总地来看，可归结为两个层面的研究工作[3–5]，一是物理机理层的研究，即首先假定海表面服从某种理论模型(如1阶、2阶海表面模型等)，在一定的参数范围内(如波段、极化、海况、擦地角等)，利用电磁散射理论与海表面模型，计算海面后向散射回波并研究海杂波特性；二是试验数据层的研究，即根据研究需求开展基于实际海面或造浪池的海杂波测量试验，利用海杂波试验数据分析海杂波特性及其随雷达参数、海洋环境参数等多种因素的变化趋势，并在考虑部分机理或不考虑机理的情况下建立海杂波模型。这两部分研究为互补关系，在海杂波认知中发挥的价值无法相互替代。依赖于电磁散射理论的海杂波特性认知具有参数可控、可重复性强等优势，所得到的海杂波特性认知结果可为基于测量数据的海杂波特性认知奠定理论基础，并通常具有很高的指导意义。然而，其主要局限性在于：由于海表面组成成分复杂，且影响因素众多、自由度大，基于机理建模得到的认知结果通常难以逼真反映实际情况。因此，利用不同雷达参数、海洋环境参数条件下的海杂波测量数据开展海杂波特性认知研究是一种贴近实际且被广泛采用的研究方法，其可验证海杂波散射机理研究成果，弥补机理研究的不足。

本文主要关注数据层的研究，在系统性梳理较有代表性的海杂波测量试验的基础上，围绕海杂波幅度分布特性、谱特性、相关性以及非平稳与非线性特性4个层面的研究内容，回顾和总结了海杂波特性认知研究进展及主要研究结论，并展望了有待于进一步研究和探索的问题。

2 海杂波测量试验概述

在过去的数十年里，相关研究机构已经分别针对星载、机载、舰载和岸基等多种平台开展了专项海杂波测量试验(包括外场试验和造浪池试验)，获取了大量海杂波测量数据，以有效支撑海杂波特性认知研究。

2.1 外场海杂波测量试验

从公开文献来看，较为典型的外场海杂波测量试验有美国海军研究实验室(NRL)的机载四频率(分别为UHF, L, C和X波段)雷达海杂波测量试验[6]、美国海军与美国国防部高级研究计划署(ARPA)的山顶计划(MountainTop Program)[7]、美国空军研究实验室(AFRL)与美国Northrop Grumman公司牵头的多通道机载雷达测量(MCARM)计划[8]、美国海军空战中心的多波段(UHF, L, S, C, X和Ku波段)雷达小擦地角(LOGAN)海杂波测量试验[9]、加拿大McMaster大学的X波段IPIX雷达海杂波测量试验[10]、南非科学和工业研究理事会(CSIR)的X波段Fynmeet雷达海杂波测量试验[11]、英格兰南海岸多波段(S, X和Ku波段)雷达海杂波测量试验[12]、西班牙南海岸Ka波段线性调频连续波(LFMCW)雷达海杂波测量试验[13]、澳大利亚国防科技署(DSTO)的海杂波测量试验[14–28]等。除此以外，美国Sandia国家实验室、华盛顿大学、英国Thales公司、伦敦大学、比萨大学、荷兰国家应用科学研究院(TNO)等国外研究机构[29–38]，以及国内的众多科研院所(如中电14所、38所、22所、西电、成电、海军航空工程学院等)在海杂波测量与特性认知方面也具有一定的技术积累。

以DSTO的研究为例，该单位自1998年起全面涉足海杂波特性认知方面的研究，以有效支撑其武器装备的发展或升级项目[14–28]。在图1(a)、图1(b)中，分别给出了用于海杂波测量的S和L波段试验雷达系统实物图。在表1中，对DSTO在海杂波特性认知方面所公开发布的技术报告进行了简要汇总。从其研究内容来看，该单位已经利用自行研发的多波段、多极化、多平台试验雷达开展海杂波测量试验，并围绕海杂波特性分析、建模、参数估计、海杂波仿真等多个层次开展了持续性、系统性的海杂波特性认知研究及其在目标检测中的应用研究，所涉及的研究内容涵盖均值散射系数、幅度分布特性、时间/空间相关性、多普勒谱特性等多个方面，其研究成果在同类研究中具有非常重要的参考价值和借鉴意义。

由于技术保密等原因，除IPIX雷达海杂波测量数据外，其余外场测量数据大多未公开发布。IPIX数据有两大集合[10,39]，一是1993年在加拿大新斯科舍省南部城市Dartmouth的测量数据，试验时雷达从峭壁上俯视大西洋，纬度/经度为44°36.72'N/ 63°25.41'W，架设高度距平均海平面约30 m；二是1998年在加拿大安大略湖畔Grimsby的测量数据，试验时雷达从岸上俯视安大略湖，纬度/经度为43°12'41.0''N/79°35'54.6''W，平台高度为20 m。由IPIX数据得到的海杂波特性分析结论将在后续各节给出。

2.2 造浪池海杂波测量试验

除外场试验外，利用造浪池开展海杂波测量试验是另一种重要的海杂波数据获取手段。尽管计算机模拟出的水面环境难以真实还原实际的复杂海洋环境，但是由于可控因素较多、可重复性强，因此便于开展系统性的定量分析，在探索不同波浪类型的后向散射机理及其回波特性等方面的研究中具有一定的优势。

图1 DSTO的试验雷达系统Fig. 1 Experimental radar systems of DSTO

表1 DSTO在海杂波方面的技术报告汇总Tab. 1 Summary of technical reports on sea clutter by DSTO

在造浪池海杂波测量方面，较有代表性的是美国加利福尼亚大学海洋工程实验室(OEL)开展的试验，又称为UCSB试验[40]。该试验采用的造浪池长53.34 m，宽4.27 m，深2.13 m，利用机械式波浪发生器或风扇，可产生出多种不同类型的波浪，其波长在1～4 m之间可控。该造浪池配置两套不同的雷达系统，分别为MIDAS雷达和C波段调频连续波(FMCW)雷达，以获取不同参数影响下的海杂波测量数据，满足多样化的海杂波特性认知需求。MIDAS雷达为脉冲多普勒(PD)体制，带宽为500 MHz，工作频率可在3～94 GHz之间设置，HH/VV双极化，脉冲重频(PRF)为2 kHz，擦地角变化范围为3°～24°。FMCW雷达的擦地角固定为6°，带宽可在125 MHz～4 GHz之间设置，PRF为1 kHz，在脉冲之间极化捷变，对于每个极化通道，无模糊的多普勒带宽为±250 Hz。与雷达同步的水面实时影像由高速摄像设备获取。该造浪池测量的海杂波数据在电磁散射计算结果的试验验证、海杂波多普勒谱分析及其机理研究等方面均发挥了重要价值。

除UCSB试验以外，东京大学工业科学学院(IIS)在2005年利用其海洋工程造浪池也开展了海杂波测量试验[40]。该造浪池长50 m，宽10 m，采用的雷达类型为连续波散射计，散射计安装在转台上，在方位和俯仰方向都可以转动。IIS雷达系统的主要参数如表2所示。在无风或有风条件下，一共产生了41种不同类型的波浪，包括规则波(Regular waves)、孤立波(Solitons)、聚焦波(Focussing waves)、Benjamin-Fier型碎浪等。该试验数据有效支撑了海杂波多普勒谱特性及其随擦地角、方位角之间依赖性的研究。

表2 IIS雷达系统主要参数Tab. 2 Main parameters of the IIS radar system

3 海杂波幅度分布特性认知

从统计学角度研究海杂波幅度分布特性无论在过去还是当前都属于海杂波特性认知研究中的重点关注对象，其所涵盖的研究内容主要涉及实测海杂波经验分布特性及其随雷达参数和环境参数的变化规律、幅度分布建模与参数估计、以及特定场景和雷达参数条件下的海杂波仿真问题。通过海杂波幅度分布特性认知所建立的幅度分布模型对目标检测算法的优化设计、恒虚警(CFAR)检测器中检测阈值的选取等问题具有重要的理论指导意义。目前，国内外已经围绕该问题展开了系统深入的研究，并在部分考虑或不考虑海表面散射机理的情况下，结合实测海杂波的时域起伏和经验分布特性(如动态范围、偏斜程度、拖尾程度等)，建立了一系列统计模型，包括幅度分布模型(又称为单点统计模型或1阶统计模型)和多维联合概率分布模型。其中，前者描述了单个距离单元内海杂波包络的统计起伏规律，而后者描述的是包络检波前一个相干处理间隔(CPI)内海杂波复矢量的联合分布特性，它在前者的基础上考虑了海杂波在不同脉冲之间的时间相关性，在模型中通过协方差矩阵实现对该相关性的定量描述。

3.1 典型幅度分布模型及其适用性

在幅度分布建模方面，瑞利模型是最早应用的海杂波模型之一，其理论基础是统计学中的中心极限定理(CLT)。将瑞利模型应用于海杂波建模时要满足如下几点基本假设：雷达分辨单元内不同散射体之间统计独立；散射体数目巨大，且不存在占据主导作用的散射体；分辨单元内两散射体与雷达距离之差比分辨单元尺寸小很多；分辨单元内天线增益为常数。历史海杂波数据的统计分析结果表明，瑞利模型主要适用于中等或较高擦地角条件下低分辨率雷达海杂波的幅度分布建模。为有效提升雷达检测性能，现代雷达往往采用较高的距离分辨率，其主要优势在于减小了散射单元面积，提高了信杂比，为低可观测目标探测提供了可能。然而，高分辨率海杂波具有更加复杂的特性，其幅度分布往往严重偏离瑞利模型，表现为尖峰和拖尾的增强，以及标准差-均值比的明显增加(对于瑞利模型，该比值为0.523)，且在小擦地角条件下更加显著。散射机理层面的研究结果证实，这种非瑞利分布特性与海浪结构所引起的散射体聚束现象有关[29]，这意味着，在小时间尺度上CLT仍然适用，非瑞利海杂波是局部瑞利分布海杂波受到调制的结果。为提高理论模型与测量数据经验概率密度函数(PDF)之间的吻合度，一些双参数或三参数非高斯模型，如对数正态、韦布尔、K、GK分布等，在海杂波幅度分布建模得到应用。

对数正态分布模型较早出现在Trunk和George等人的研究中[41,42]，适用于动态范围较大、拖尾程度较重情况下的海杂波建模问题。韦布尔分布模型的拖尾程度介于瑞利模型和对数正态模型之间，适用于较为均匀情况下的海杂波建模问题。K分布模型在海杂波建模中的应用得益于Trunk等人的重要研究结论[43]，即某些类型的非瑞利海杂波可以建模为局部均匀的瑞利模型，其功率水平被海表面的大尺度空间采样所调制。由该结论发展而来的海杂波模型即为瑞利混合模型，又称为复合高斯模型，它是一个分布族，在海杂波功率水平的分布函数给定后就可以得到模型的具体表达式，K分布即为其特例之一。1976年，Jakeman和Pusey从海表面散射现象学出发，在海杂波建模为2维随机游走模型的假定下，基于随机散射场相干叠加数学描述推导出了K分布模型，并首次将其应用于海杂波建模[44]。1994年，Sangston等人通过严格的数学推导建立了复合高斯模型与2维随机游走之间的理论关系[45]。

目前，公开文献已利用大量海杂波测量数据，对上述典型模型的适用性和模型参数变化趋势展开了深入研究[12,46–48]，研究结果表明，由于不同雷达参数及海洋环境参数条件下海杂波幅度分布特性存在较大差异，且不同模型在动态范围、拖尾程度上各异，因此目前不存在一个通用的模型形式来概括已有的幅度分布模型。除对数正态分布以外，上述非高斯模型均为复合高斯模型的具体形式。复合高斯模型建立在复合表面理论的基础上，因同时兼备机理可解释性和数学易操作性，在海杂波建模及后续的雷达信号处理领域中得到了广泛应用[49,50]。从数学形式上看，复合高斯模型可表示为两个相互独立分量乘积的形式，两个分量分别称为散斑分量和纹理分量。散斑分量是零均值、有可能相关的复高斯过程，描述了海表面小尺度张力波的散射特性；纹理分量是实的非负随机过程，描述了海表面大尺度重力波的散射特性。

3.2 K分布及其半经验参数模型

在复合高斯模型中，如果纹理分量建模为平方根Gamma模型，则海杂波幅度满足K分布模型。由于K分布在大部分条件下均能较好的拟合实测海杂波，因此相关研究人员试图建立K分布参数的半经验模型，以提高应用的灵活性。需要注意的是，对于不同的试验数据，由数据拟合直接估计得到的分布参数与半经验模型给出的预测值可能具有偏离，但是对于给定的参数集合，如擦地角、分辨率、极化等，半经验模型给出的预测值可以作为典型的参数平均值使用。

K分布尺度参数与海杂波的局部功率水平有关，它可以通过杂波的均值散射系数(典型的模型有SIT, GIT, TSC, HYB和NRL等)、雷达参数(如波长、天线波束宽度和脉宽等)和几何位置参数等先验信息计算得到[14]。

K分布形状参数与海杂波的尖峰和拖尾程度有关，拖尾越重，形状参数就越小。形状参数的半经验模型最初由Ward等人给出[29]，在统计分析300批次距离分辨率为4.2 m的机载海杂波试验数据的基础上，建立了形状参数随擦地角、切向分辨率、涌浪方向和极化之间的经验关系模型。后续研究对Ward模型进行了修正，通过引入余弦函数形式的方向依赖因子来描述形状参数随涌浪方向的变化[51]，以提高模型的灵活性和适用范围。在1990年，Ward和Wicks给出了形状参数的另一种半经验模型，模型中涉及3个未知参数，可采用最小二乘法拟合得到[51]。Ward-Wicks模型在适用性上优于Ward模型及其修正型，但是对于任意涌浪方向条件下的海杂波数据，该模型无法准确预测出形状参数。以上两种模型仅适用于脉宽为28 ns的海杂波数据，考虑到脉宽对海杂波幅度分布拖尾的影响，Ryan和Johnson在Ward模型的基础上加入了脉宽修正因子，以使模型适用于脉宽大于28 ns情况下的海杂波数据[52]。上述半经验模型仅适用于X波段且脉宽大于28 ns的场景，在其它情况下，尚不存在K分布形状参数的半经验模型。

通过大量实测海杂波数据的统计分析，并结合K分布形状参数的半经验模型，可以得到如下几点结论[14]：①同等条件下，HH极化海杂波的形状参数小于VV极化；②擦地角越小，形状参数也越小；③当波束方向顺着或逆着涌浪方向时，形状参数较小，侧视涌浪方向时形状参数较大，在其它方向上形状参数介于两者之间；④随径向距离的增加，切向距离单元的尺寸增加，形状参数出现变大的趋势；⑤形状参数随海况、风速、或视线方向与风向夹角之间的统计趋势较弱。

3.3 球不变随机过程模型

在自适应相干检测领域，通常较为感兴趣的是包络检波前海杂波复矢量的联合分布特性。由于纹理分量具有较长的相关时间，因此，当观测时间和雷达系统的CPI相近时，纹理分量可近似建模为随机常数，此时，复合高斯模型简化为球不变随机过程(SIRP)，海杂波整体的相关性与散斑分量一致。对SIRP采样，就可以得到球不变随机矢量(SIRV)。SIRV的联合PDF由均值矢量、协方差矩阵和1阶特征PDF共同确定，其在杂波建模以及自适应检测中的广泛应用主要得益于以下3个原因：一是该模型与海杂波测量数据的经验分布特性较为一致；二是该模型在某些线性变换下能保持PDF的不变性，如典型的MTI处理；三是该模型属于外生模型，在海杂波仿真时可以独立控制边缘PDF和协方差矩阵[53,54]。

在文献[48,55,56]中，分别提供了两种不同的检验方法以测试海杂波测量数据与SIRV模型的兼容性。检验结果表明，在显著性水平为0.05的情况下，IPIX雷达海杂波数据不能拒绝SIRV模型的假设；同样，对于美国山顶计划海杂波数据，距离上临近的采样矢量可以采用独立SIRV模型描述，即纹理分量在不同距离单元之间完全相关。在基于广义似然比(GLRT), Rao检验等检测准则的自适应检测器设计时，为得到封闭的检验统计量表达式，通常假定SIRV模型中的纹理分量为确定性未知量，而非随机常数[57]。

3.4 幅度分布拖尾建模

在高分辨率、小擦地角等条件下，海杂波幅度分布出现重拖尾的概率明显增加，利用已有典型海杂波幅度分布模型难以有效解决拖尾建模问题[58,59]。由DSTO的研究报告可知，这种现象在大擦地角条件下也会出现[19]。例如，在图2中，给出了一组S波段、HH极化小擦地角海杂波的经验概率分布函数(CDF)曲线及已有模型的建模结果，其中，纵坐标表示1-CDF域，它等同于虚警概率的含义[46]。图中所示的GK和GK-LNT模型分别为纹理分量建模为广义Gamma分布和对数正态分布情况下复合高斯模型的特例[48]。

图2 幅度分布建模结果Fig. 2 Amplitude distribution modeling results

可以看出，对数正态分布的收敛速度过慢，整体的拟合误差较大，而韦布尔、K、GK和GKLNT分布在小幅值区域，即虚警概率小于10–2时，能够取得较为满意的建模效果，但是当虚警概率低于10–2时，理论模型逐渐偏离测量数据的经验CDF曲线，出现较大的建模误差。在CFAR检测器设计或性能分析时，对于给定的虚警概率，若利用复合高斯理论分布模型设置检测门限，则门限将明显过低，导致检测结果中出现的虚警数大于预期。由此可见，作为稳健的幅度分布模型，应同时能够对海杂波幅度分布的全局PDF以及PDF的拖尾区域实现精确拟合，且拖尾部分的拟合精度往往具有更加重要的意义。显然，对于该组数据，上述理论分布模型尚不具备这种稳健性。

已有研究成果表明，海杂波幅度分布拖尾部分与理论建模曲线的偏离主要与海杂波中间断出现的海尖峰现象有关[60]。海尖峰在时域通常表现出类似于冲激信号的特性，其持续时间可长达秒量级，给检测器设计带来一定的挑战[61–69]。海尖峰观测试验的研究结果证实，约占据80%的海尖峰与海表面的碎浪或白浪有关[63]，其对应海表面的非Bragg散射机理。在海尖峰背景下，倾斜调制的Bragg散射分量和海尖峰分量是构成海杂波的两个独立分量[68]，从这点来看，已有复合高斯模型在散射机理层面并未考虑后者对幅度分布特性的贡献，因此在描述拖尾现象上仍具有一定的不足。

为有效解决拖尾建模问题，公开文献提出了一系列幅度分布模型，总体来看这些模型可分为两类，第1类试图在重力波/张力波散射分量的基础上以线性叠加的形式增加额外的散射分量，以考虑海尖峰对拖尾的贡献，例如KA, KK, WW, ε-高斯模型等[70–77]；第2类则是在复合高斯的理论框架内，通过采用数学上更潜力描述拖尾现象的PDF对模型中的两个分量进行建模，以实现建模精度的改善，例如广义Gamma分布纹理、逆Gamma分布纹理、逆高斯分布纹理建模的复合高斯模型及广义复合(GC)分布模型等[78–83]。第1类模型通常具有较多未知参数，而第2类模型通常不存在封闭形式的PDF表达式，在实际应用时应根据研究需求择优选择拖尾模型。除上述模型以外，稳定分布模型、K+瑞利分布模型、Pareto分布模型、Pareto+噪声分布模型及非广延分布模型等在拖尾建模中均得到应用，有效改善了建模精度[84–90]。

3.5 模型参数估计和海杂波仿真

ML估计是较为通用且广泛使用的参数估计方法，但大多数模型通常不存在封闭表达式，给实际应用带来较大不便。为此，矩估计方法得到大量应用，利用模型的各阶矩，可以将参数估计问题转化为简单的代数方程求解问题[18,91]。

若幅度分布模型中的未知参数较多，则采用单一方法通常难以估计出模型中的所有未知参数，此时可以采用“两步法”求解，即根据模型形式，在第1步先通过搜索或优化方法估计出部分参数，以此为基础，在第2步估计出剩余未知参数[30]。以典型的3参数GK分布模型为例，其包含形状参数、尺度参数和功率参数，在第1步估计中，根据2～5阶矩估计值，利用最优搜索方法(如Nelder-Mead单纯形法)首先估计形状参数和功率参数，将其代入PDF表达式后，再利用1阶矩方法通过简单的代数运算估计出尺度参数。若模型中包含更多未知参数，如KA和KK模型，其参数均多达5个，此时需在分析模型各参数对总体分布特性影响的基础上，结合实测海杂波的经验分布特性，对部分参数进行简化处理，以降低参数估计的复杂度。

在仿真方面，目前关注较多的是复合高斯海杂波仿真问题，较为常用的仿真方法包括零记忆非线性变换法(ZMNL)和SIRP法[92]。在非高斯海杂波仿真中，除了关注幅度分布特性和时间相关性外，还需关注不同距离单元之间纹理分量的空间相关性、谱的时变非平稳特性等，使之尽可能与实际海杂波特性匹配。因此海杂波仿真是一项极具挑战性的工作，目前较有代表性的成果可参考Davidson, Watts, Dong等人的研究工作[25,33,93]。

从该部分研究现状来看，海杂波幅度分布特性认知已取得较大进展，分布模型已在韦布尔、K等已有典型模型的基础上得到很大程度的完善和发展。然而，在解决拖尾问题上，仍然缺乏体系化的建模方法，同时，幅度分布模型如何真正应用于CFAR检测和自适应检测领域，以便于从理论上指导检验统计量设计和门限形成，仍是有待于进一步解决的重要理论问题。

4 海杂波谱特性认知

海杂波谱是多个概念的统称，既可以指海杂波的幅度谱、相位谱，也可以指功率谱、高阶谱等。一般而言，公开文献中提到的海杂波谱通常是指功率谱[2]。由于海表面呈现出永无止境的运动状态，再加上天线扫描调制以及雷达平台运动等因素的影响，海杂波谱将产生多普勒频移，因此，海杂波功率谱又称为多普勒功率谱，或简称为多普勒谱。

从数据层面出发，已有公开文献围绕海杂波谱特性认知问题主要开展了3个层面的研究工作。一是海杂波谱基础特性及其机理阐述，该研究主要从谱形状及参数等方面掌握海杂波谱的基础特性，为海杂波谱建模和相参海杂波仿真提供支撑。二是持续较长时间结构的平均谱形状建模问题，所关注的时间尺度大于海表面的重力波周期，一般为秒量级以上，在该尺度上，海杂波谱随时间的起伏变化特性在谱估计阶段被平滑，因此研究结果仅能反映海杂波能量在不同频点的总体分布情况，海杂波谱的时间非平稳性信息缺失。为进一步探索海杂波谱随时间变化的精细化信息，还需在此基础上开展第3个层面的研究，即短时局部谱研究，主要涉及谱形状建模及各多普勒门内谱的起伏性描述，其所关注的时间尺度小于重力波周期，大于碎浪和白浪的相关时间，约为十分之一秒量级。

4.1 海杂波谱基础特性及其机理阐述

谱基础特性研究包含十分丰富的内涵，其中，Pidgeon, Lee, Ward, Watts以及Lamont-Smith等人的研究较有代表性。Pidgeon的主要贡献在于利用C波段小擦地角海杂波发现了谱峰分离现象[94]，该现象表明小擦地角条件下Bragg散射并非唯一占据主导地位的散射分量。事实上，受遮挡和多径效应的影响，除Bragg散射外，白浪散射、镜面散射均会对后向散射做出一定的贡献，它们主要与海杂波数据中观测到海尖峰相关联，其散射机理可描述为非Bragg散射，对应的散射体称为快散射体，该类散射体在多普勒速度上大于Bragg散射体(慢散射体)，且在HH极化时占据主导，因此导致HH极化海杂波的谱峰出现在较高频点上[40]。

从散射机理上看，在微波波段，Bragg散射分量源于粗糙海面的小尺度张力波，而非Bragg散射分量主要源于碎浪的波峰。随着张力波接近或远离雷达视线方向，在频域将出现两条Bragg谱线，分别位于正负频率处[50]。对于L及L以下波段海杂波数据，谱观测结果通常与该理论结果相符。然而，对于L以上波段海杂波谱，通常在频域只出现一个偏离零频的谱峰[46]，这主要是Bragg散射体与中等尺度波浪和长波散射体耦合的结果。其中，中等尺度波浪的轨道速度具有一定的扩展，导致海杂波谱在Bragg谱线附近展宽，在大多数海洋环境条件下，轨道速度导致的谱展宽效应比Bragg谱线的分离更加显著，而长波则根据其自身的轨道速度对多普勒谱进行平移。在其综合影响下，海杂波谱出现了上述特征。实际上，Lee等人的研究指出[95]，除波浪速度扩展引起的谱展宽外，还存在第2种谱展宽机理，即受生存周期控制或阻尼控制的谱展宽，它与散射体的有限生存周期有关。

在海杂波谱基础特性研究方面，Lamont-Smith等人的研究具有持续性，涉及的研究内容较为系统深入[40,96–99]。研究过程中采用的海杂波数据包括英国南海岸Portland悬崖顶部的海杂波测量数据和基于造浪池(包括UCSB和IIS造浪池)的海杂波测量数据，且部分研究结果与电磁散射计算结果进行了对比和验证。其主要研究结论为：①随擦地角增加，多普勒速度减小，两者近似为线性变化关系；②慢散射分量一直存在，在VV极化时占据主导，它具有较窄的谱；③快散射分量随机出现的时间只占据约20%，在其出现的多普勒门内具有较大的归一化方差，其多普勒速度与雷达视线方向上碎浪的相速度有关；④多普勒谱峰的不对称性是由快散射分量和慢散射分量很少准确对齐引起的；⑤海杂波时域的拖尾程度与多普勒谱宽之间没有必然联系。

最后，需要说明的是，在中等以上擦地角(10°以上)条件下，海表面散射机理异于小擦地角条件，具体表现为：Brewster角抑制效应不再显著，削弱了多径的影响，占据主导作用的散射分量为粗糙海面的Bragg散射，以及少量的白浪散射。机理层面的差异导致小擦地角海杂波谱特性分析结论或模型未必适用于大擦地角条件。

4.2 平均谱形状建模研究

平均谱形状建模所关心的时间尺度一般为秒量级以上，以保证观测数据至少能够涵盖一个完整的重力波周期[32]。高斯模型是较早应用且受到广泛关注的模型之一，该模型除用于平均谱形状建模外，在短时局部谱分析中也得到大量应用。除高斯模型外，指数模型、幂率模型也是常用的平均谱形状模型。为使模型能够适用于多样化的海杂波测量数据，在考虑Bragg和非Bragg散射机理的前提下，海杂波平均谱形状模型已经从最初的高斯模型、幂率模型等简单模型发展到Lee模型[95,100]、Walker模型[101,102]、Lamont-Smith模型[97]及Rosenberg模型[103]等多分量混合模型，其中，后两种模型均可视为Walker模型的修正形式。

Lee模型分别考虑了Bragg和非Bragg散射分量对谱的贡献，在建模时将平均海杂波谱分解为3种不同类型的基函数，分别为高斯、Lorentzian和Voigtian，其中，Voigtian谱是高斯和Lorentzian谱卷积的结果[95,100]。Walker在Lee模型的基础上对平均谱形状模型进行了修正和简化，提出了数学上更易操作的三分量混合高斯模型[101,102]，3种分量分别描述了Bragg散射、白浪散射和海尖峰散射的谱特性，并以线性叠加的形式构成海杂波谱形状模型。当雷达平台运动时，文献[104]对Walker模型进行了修正，以考虑平台运动对多普勒谱的影响。Lamont-Smith模型可视为Walker模型的简化形式，该模型最多包含两个高斯分量，用来描述快散射分量和慢散射分量的贡献[97]。Rosenberg模型为Walker模型在大擦地角条件下的改进型[103]。在该条件下，海杂波中的白浪和海尖峰分量明显弱于Bragg分量，因此Walker模型并不适用。在Rosenberg模型中，白浪和离散的海尖峰分量建模为高斯模型，且在HH/VV极化条件下均存在，在此基础上叠加另一高斯模型以描述慢速Bragg散射分量的贡献。

4.3 短时局部谱研究

短时局部谱可以精细刻画海杂波谱的时间非平稳性和空间非均匀性，正确认识该特性是有效评估协方差矩阵估计性能、自适应检测器的CFAR特性以及目标检测性能的前提[39,105]。

短时局部谱形状通常建模为单分量高斯模型，在其关注的时间尺度内，海杂波局部功率水平可近似描述为随机常数，且不同时间段之间海杂波局部功率水平起伏变化，因此，利用该随机常数对高斯模型进行功率调制，就可以得到短时局部谱模型。然而，若仅考虑功率调制，则海杂波在所有多普勒门内的统计特性完全相同，这显然与海杂波测量数据的NSIM分析结果不一致[29]。实际上，除功率调制外，受海表面状态、风速/风向等复杂海洋环境参数的影响，短时局部谱的谱宽和中心频率均受到调制，表现出一定的随机起伏，且部分参数之间具有一定的依赖关系，在建模过程中需综合考虑这种依赖关系。

针对该问题，Miller, Ward及Watts等人给出了短时谱建模的新方案[32,106–109]。Miller采用变化系数来分析海杂波，在此基础上建立了短时局部谱形状模型[106]。Ward将海杂波短时局部谱建模为随机功率常数调制的两分量混合高斯模型，以描述Bragg散射、Burst散射和白浪散射分量[32]。Watts进一步深入研究了短时谱特征参数的耦合关系，建立了更加贴合测量数据的模型[33,107]，即，在幅度分布建模为K分布模型的基础上，将谱的局部功率水平建模为Gamma分布模型，谱形状采用高斯基函数建模，其谱宽本身也是高斯分布的随机变量，而中心频率则是一个与局部功率水平线性相关的Gamma分布随机变量。该模型的有效性已经得到X波段Fynmeet雷达小擦地角海杂波测量数据的验证，且在相参海杂波仿真、自适应检测算法性能评估等领域得到应用[33,105]。在文献[108,109]中，Watts等人对该模型做了修正和完善，以使其适用于中等擦地角条件下的海杂波测量数据。

除谱形状建模外，各多普勒门内谱的起伏性描述也是短时局部谱的重要研究内容，其研究结果直接关系到频域目标检测算法中的CFAR门限设置。Baker较早认识到了海杂波谱的非高斯特性，即，时域非高斯海杂波变换到频域后，在不同多普勒门内具有非高斯统计特性[110]。其研究结果表明，时域K分布模型同样适用于描述单个距离-多普勒门内海杂波谱的统计建模问题，且该模型在描述其相关性方面具有一定的灵活性。此外，不同多普勒门内K分布尺度参数c和形状参数v均发生变化，这与Ward等人采用NSIM得到的分析结果一致[29]。形状参数的较小值主要出现在谱峰边缘区域，该区域内多普勒功率水平较低，但是起伏较为剧烈，在分布特性上具有显著的拖尾。该现象主要与谱宽的随机起伏以及多普勒中心频率的变化有关[29,108]。在文献[111]中，利用X波段机载海杂波测量数据开展类似的分析，结果表明不同距离单元之间形状参数随频率之间同样表现出相同的变化规律。在频域CFAR门限设置时，如何充分考虑不同多普勒门内海杂波谱的尖峰和拖尾程度，以有效控制虚警数，是有待于进一步解决的重要问题。

4.4 其它层次的谱研究

随现代信号处理理论和方法的不断发展和完善，海杂波谱特性认知涉及的内容也得到了扩展，除上述研究内容外，还可从更多层次上认知海杂波谱特性，包括时变AR谱[50]、双谱[112]、WVD时变谱[113]、Hilbert谱[114,115]、分数阶功率谱(FPS)[116]等。以FPS为例，它反映了随机信号功率谱在分数阶Fourier变换(FRFT)域的变化和分布情况，非常适合分析时变随机信号。采用FPS能够从本质上反映海面散射回波信号的功率谱在FRFT域的变化和能量分布，进而分析海杂波中快散射体对应的非Bragg散射分量谱特性。上述谱特性分析结果可辅助用于特征域目标检测方法设计。其总体思路为：提取和筛选出一系列能够区分海杂波单元与目标单元的差异特征，通过特征抽取和特征筛选将海杂波映射到低维特征空间，并在特征空间中选取一个能包含大多数海杂波特征向量的区域，以便有效分离目标和海杂波的回波特征，实现目标检测的目的[114,115]。

5 海杂波相关性认知

在高距离分辨率条件下，海杂波的时间-距离2维平面图上会表现出明显的纹理结构，不同脉冲或不同距离单元之间不再是统计独立的关系，此时，基于单点统计特性的海杂波模型往往具有一定的局限性，且模型层面的偏差通常会对雷达目标检测性能造成不利影响[20,117]。为提高模型的拟合精度，必须充分考虑海杂波相关性，其反映了不同脉冲或不同空间位置海杂波之间的线性依赖程度，其中，同一距离单元、不同脉冲之间的相关性称为时间相关性，不同距离单元之间的相关性称为空间相关性，包括距离向空间相关性和方位向空间相关性。海杂波相关性一般采用相关函数或其归一化形式(即相关系数)进行定量描述，当相关系数从1衰减为1/e时，对应的时间间隔(或距离间隔)称为相关时间(或相关长度)[20]。

5.1 时间相关性

从复合表面理论散射机理可知，在不同时间尺度上，海杂波时间相关性差异显著[118]。在小时间尺度上，即观测时间约在雷达系统的CPI量级时，时间相关性主要与复合高斯模型中的散斑分量有关，其相关时间为毫秒量级。在大时间尺度上，即观测时间约在海浪的主波周期量级时，时间相关性主要与纹理分量有关，其相关时间为秒量级。

由维纳-辛欣定理可知，短时时间相关性与海杂波多普勒谱、协方差矩阵之间为一一对应的关系，因此时间相关性分析结果可从时域角度揭示海杂波谱的基本特性。由于海杂波多普勒频移通常不为零，因此时间相关系数的虚部不可忽略。若谱形状中出现两个分离的谱峰(L及L以下波段海杂波谱通常为该情况)，则时间相关性分析结果仅能揭示功率水平较大的谱峰特性[46]。短时时间相关性分析结果表明，其主要与雷达波段、极化、雷达体制、擦地角、风向等因素有关，其主要研究结果为[22,46,47,118]：①VV极化的相关时间通常大于HH极化；②随雷达工作频率的减小，相关时间增加，对于X和S波段雷达，其典型值分别为10 ms和30 ms量级[46]；③频率捷变对海杂波谱具有白化作用，使海杂波变得完全不相关；④随擦地角增加，相关时间变长；⑤在相同擦地角条件下，逆风向海杂波较其它方向具有更长的相关时间。在文献[103]中，通过大量海杂波数据的统计分析，还建立了HH/VV极化条件下相关时间随风速和波高之间的半经验关系模型。

长时时间相关性本质上反映的是纹理分量的相关性，在分析时首先需要对海杂波进行平滑，以消除散斑分量的影响。时间相关系数首先表现出一个缓慢的下降期，然后是一个持续较长时间的周期性缓慢衰减，其周期性主要与海表面的涌浪结构有关。文献[118]利用C, X和Ku波段高分辨率海杂波数据分析了长时时间相关性，结果表明其与波段、距离分辨率无关，与极化有一定的关系，其中，VV极化时周期性调制特征更加显著。文献[17]利用X波段Ingara雷达在澳大利亚南海岸测量的海杂波数据，分析了VV极化条件下逆风/逆浪、侧风/侧浪以及视线方向介于两者之间这3种情况下的长时时间相关性，结果表明：在逆风/逆浪情况下，相关系数起伏周期最长，约为11 s量级，与观测到的涌浪周期完全一致；在侧风/侧浪情况下，相关系数起伏周期最短，约为3 s量级，这主要是因为切向分辨率较低，随涌浪在波束之间的运动，在时间上仅能分辨结构大于切向分辨率的涌浪成分；在其它方向上，相关系数起伏周期介于两者之间，约为7 s量级。在文献[33]和文献[49]中，分别分析了Fynmeet雷达和VV极化条件下IPIX雷达海杂波的长时时间相关性，结果表明其相关系数的起伏周期分别为10 s和6.5 s。

在建模方面，短时时间相关性模型可直接通过多普勒谱模型的逆傅里叶变换得到，因此在海杂波仿真或自适应检测器性能分析中，通常采用高斯模型建模。此外，指数衰减模型、幂率模型等也得到了应用[119]。而在长时时间相关性方面，目前更多关注的仍然是特性描述及其在海杂波仿真中的应用[33]，尚不存在有效的模型形式来描述其周期性衰减特性，因此仍需开展进一步研究。

5.2 空间相关性

海杂波空间相关性同样与尺度密切相关，在较小的空间尺度上反映的是散斑分量的空间相关性，其固有的粗糙特性导致不同距离分辨单元上的散斑分量通常是不相关的，而在较大的空间尺度上反映的则是纹理分量的空间相关性，其主要与海表面的涌浪结构有关，且两者的相关距离在同一量级[17]。从严格意义上讲，海杂波空间相关性还同时受时间因素的影响，其中，对于距离向空间相关性，由于测量数据的时间间隔很短，所以可以忽略其时间相关性，而方位向空间相关性则不可忽略，其反映的是时间与空间耦合影响下的总体相关性。

空间相关性对雷达目标检测性能的影响很大，比如，若不能准确估计海杂波相关距离单元个数，将导致CFAR检测器中参考单元数选取的盲目性，从而无法获取最优CFAR增益，引起目标检测性能损失[120]。

在空间相关性理论研究方面，Marier[92], Raghavan[121]以及Lombardo[122]等人的研究较有代表性。在幅度分布满足复合高斯的假定下，利用概率论的基本原理和方法，推导得到海杂波幅度的空间相关系数与纹理分量、散斑分量空间相关系数之间的非线性关系模型。在纹理分量和散斑分量空间相关系数分别已知的情况下，可依据该模型计算海杂波幅度的空间相关系数。然而，该理论关系模型结构复杂，且缺乏实测数据验证，因此仅在海杂波仿真中得到部分应用。

在基于测量数据的研究方面，Watts等人在1987年采用频率捷变雷达的海杂波测量数据对空间相关性开展了研究[123]，并提出了半经验关系模型和指数衰减模型。该雷达距离分辨率为4.2 m，而距离采样间隔为2.6 m(属于过采样情况)，每个序列包含大约250个距离采样点。在计算相关系数时，为消除散斑分量的影响，每个距离单元的数据采用100个连续的脉冲进行平滑，得到平均幅度序列，取平方后得到平均强度序列，并计算其相关系数。最后，采用100个连续的序列对相关系数取平均，得到最终的空间相关系数。Watts模型因结构简单，在后续海杂波仿真、目标检测性能评估与预测等方面得到大量应用[120]。然而，该模型仅适用于小擦地角条件，且与半经验模型关联的影响参数较少，导致其适用性受限。

此外，Armstrong, Siegel, Tough等人也分别对海杂波的空间相关性及其在目标检测、杂波仿真等领域的应用开展了研究[118,124–126]。以Siegel等人的研究为例，其研究结果表明[118]，从C到Ku波段，在逆风/逆浪条件下，海杂波空间相关性与波段和极化均无关，而在顺风/顺浪条件下，空间相关性与极化有关，其中，VV极化时相关长度更长；海尖峰的空间相关性与风向/浪向、波段和极化均无关。

空间相关性方面较为系统性的研究可参考DSTO的技术报告，其利用L, S和X波段海杂波数据，对相参和非相参条件下的距离向/方位向空间相关性开展了研究[17,20–22]，主要研究结果为：①相参条件下海杂波距离向相关长度小于雷达距离分辨率，且I/Q分量在空间上不相关；②非相参条件下，海杂波幅度的距离向/方位向相关长度分别在一个径向/方位向分辨单元之内；③海杂波强度的空间相关函数由两部分组成，第1部分为快变化散斑分量的贡献，在不同距离单元之间不相关，第2部分为慢变化纹理分量的贡献，具有较强的相关性，海杂波强度总的空间相关性主要与纹理分量有关；④在距离向，纹理分量的空间相关性在HH/ VV极化条件下具有几乎相同的周期性起伏特性，在方位向同样如此，但是起伏周期更长，该起伏周期包含了海表面涌浪结构信息；⑤逆风向条件下海杂波纹理分量的距离向相关长度大于侧风向；⑥在频率捷变条件下，距离向空间相关性几乎不受影响，而方位向空间相关性的变化较为显著。

在空间相关建模方面，指数衰减模型和幂率模型是应用较为广泛的模型形式[14,120]，这两类模型均描述了复合高斯模型中纹理分量的距离向空间相关性。在海杂波幅度分布满足K分布模型的假定下，通过理论推导还可以得到与之对应的海杂波强度距离向空间相关模型[25]。该模型可以有效描述空间相关系数在初始阶段表现出的快速下降趋势，但是实测数据的分析结果表明，在快速下降后还会出现一个缓慢的周期性衰减过程，该周期性隐含了径向上观测到的涌浪结构信息[22]。显然，已有模型难以完整描述上述特征。针对该问题，在空间相关性分析的基础上[127]，文献[128]建立了一种三参数空间相关新模型，以两分量线性加权的形式实现了空间相关建模精度的改善。

6 海杂波非平稳性与非线性认知

海杂波特性认知的已有研究大多建立在平稳假设条件下，在该假设下，海杂波相关性分析、多普勒谱估计以及协方差矩阵估计等都可以采用较为简单的方法。然而，随着雷达分辨率的提高和海况等级的增加，平稳性假设条件很难满足，海杂波所表现出的复杂特性已经从非高斯扩展到非平稳和非线性[49,50]，文献[129]将其统称为海杂波的“三非”特性，如图3所示。此时，仅采用常规统计学方法研究海杂波特性时会存在一定的局限性，需要对海杂波特性认知的理论和方法进行扩展和完善，以便于从更加深入的层次上认识和理解海杂波的复杂性及其电磁散射机理。

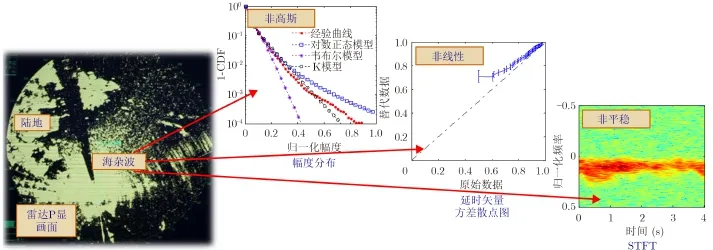
图3 海杂波的“三非”特性Fig. 3 “Tri-non” properties of sea clutter

海杂波的非平稳性主要由海表面状态的时变特性引起。非平稳性分析大多采用信号分解方法[130–132]，如经验模式分解(EMD)，通过分解可以将复杂的海杂波表示为简单的、有限个分量叠加的形式，这些分量即为固有模态函数(IMF)。此外，采用变换域方法研究海杂波非平稳性是另一种常用的思路，其研究对象主要包括动态谱、WVD和Loève谱等[113]。已经建立或应用的非平稳性模型主要包括循环平稳模型、时变自回归(TVAR)模型、突变AR模型等[50,133–135]。此外，相关文献还研究了非平稳海杂波背景下协方差矩阵的估计方法及其对自适应检测算法的性能影响等问题[39,135,136]。

对于非线性特性，从机理上看，其主要与海表面的动态结构密切相关。采用非线性理论研究海杂波特性在一定程度上丰富和发展了已有的统计学研究方法，两种理论方法相互补充，并不矛盾。已有的非线性理论主要包括混沌理论、分形理论、孤立子理论及时间序列的统计非线性理论等。在国内外已有研究中，混沌理论和分形理论在海杂波特性研究中应用较多[137–142]。

在非线性特性研究中，海杂波是否具有混沌特性还存在较大争议，经X波段实测数据证实，短时间内海杂波序列不可采用单分量混沌模型来建模，但不排除海杂波有可能是多个混沌模型复合而成[138,139]，而分形理论的研究较多，且具有一定的机理可解释性[141,142]。对于分形特性，相关研究结果表明，海表面物理结构在一定的尺度范围内具有分形特性，对人造物体等光滑和规则对象的描述是失配的，因此分形特性参数可以直观反映出海杂波单元与目标单元的差异，在目标检测领域具有一定的应用潜力。

波动分析(FA)方法是一种常用的分形特性分析方法，它刻画了时间序列的2阶统计特性。然而，当序列具有非平稳性时，FA往往无法反映出真实的标度特性[142]。针对该问题，Peng等人在研究DNA序列时提出了消除趋势波动分析(DFA)方法，通过局部趋势项的拟合和消除，为非平稳、长程幂率相关时间序列的标度特性分析提供了有效的工具[143]。目前，DFA已经在DNA序列、气象数据以及金融时间序列分析等领域得到普遍应用[144,145]。显然，在海杂波满足非平稳性的前提下，更加适合采用DFA分析其分形标度特性。例如，文献[142]从目标检测的需求出发，采用DFA研究了海杂波在3种数据域的分形标度特性，即幅度、幅度的部分和以及幅度的1阶差分，研究表明前两种数据域的分形特性在海杂波单元与目标单元具有较大差异。文献[146,147]认识到DFA结果中出现的交叉标度现象及其对目标检测的不利影响，通过最优尺度区间选取，并利用该区间内的标度指数和截距组成检验统计量，设计出一种基于联合分形特性的目标检测算法，并对检测性能进行了分析。文献[148]和文献[149]进一步采用DFA分析了波段、极化及海洋环境参数影响下海杂波的分形特性，并以分段标度指数差异为特征量设计了一种目标检测方法。

目前，海杂波分形特性认知研究已经从较为简单的单一分形特性向多角度(如多重分形特性、扩展分形特性等)和多域(如频域、FRFT域等)扩展，并对其主要影响因素进行了分析。在此基础上，通过提取和筛选能够有效区分海杂波单元与目标单元的分形特性参数，设计了一系列基于分形特性的目标检测方法，有效提升了海杂波中的微弱目标检测

性能[150–155]。

7 研究展望

海杂波特性认知既是一个共性技术问题，又是一个基础问题，在过去数十年的研究过程中，积累了很多经验和方法，也得到了大量有价值的研究结论，在目标检测方法研究中发挥了重要价值。然而，仍然存在许多有待于进一步研究和探索的基础问题和应用问题，正如《雷达手册》中海杂波章节最后总结的一样，“目前看来进展并不显著”[4]。具体来讲，可归纳为以下几点。

(1) 海杂波影响因素的深化分析

海杂波影响因素众多，如雷达参数(包括波段、波形、极化、分辨率、带宽、波束宽度、PRF等)、海洋环境参数(包括温度、盐度、介电常数、折射率、浪高、周期、涌浪方向/波长、风速/风向等)、地理几何参数(包括平台高度、擦地角、方位角等)、海域(包括深海、浅海、近海岸等)、平台类型(包括岸基、舰载、机载、弹载等)等。海杂波特性随这些因素之间有着复杂的联系，而且不同因素对海杂波特性的影响往往不是独立的，而是相互耦合的。在给出海杂波特性分析结论或模型时，需要同时明确其对应的参数集合，否则结论或模型将不再适用。例如，方位向空间相关性以PRF换算为时间表示后，Ward, Dong, Chan和Stehwien的分析结果分别为5～10 ms[2], 4 ms[20], 10 ms[46]和8 ms[47]，这种差异性主要源于海杂波测量参数的不同。再如，在中等以上擦地角条件下，占据主导作用的散射机理为粗糙海面的Bragg散射以及少量的白浪散射，而在小擦地角条件下，占据主导作用的散射机理为Bragg散射、白浪散射和镜面散射等，机理层面的差异导致小擦地角条件下的海杂波谱模型不再适用于大擦地角条件[103]。由此可见，海杂波特性认知研究是一项极其复杂的系统工程，有必要进一步开展系统、持续、深入的研究，揭示不同因素影响下的海杂波特性变化趋势，并探索海杂波参数随主要影响因素之间的半经验关系模型。

(2) 海杂波精细化建模与检测器需求的博弈

海杂波特性认知目前从总体上看更趋向于关注精细化建模问题，如精细化幅度分布或短时谱建模等。这些模型在拟合实测数据方面具有很高的精度，但是模型形式通常较为复杂，往往不能给出有效和实用的目标检测器，或者尽管可以给出与之匹配的检测器，但是有限的检测性能提升需要以运算复杂度的大幅增加为代价。事实上，实际雷达目标检测中经常遇到的近区杂波与远区杂波、陆地杂波与海杂波等杂波区域识别问题却很少有深入研究。对于运动平台的雷达，如导航雷达、机载雷达等，陆海交界处的陆地杂波对雷达系统的整体检测性能，尤其是对海岸线附近的目标检测造成了严重的影响；同时，近程海杂波区域大小在不同海况下会发生较大的变化，从而也较大程度地影响海杂波抑制方法的参数设置，而这类问题在海杂波特性认知中较少涉及。因此，精细化建模一方面需要解决理论问题，另一方面也要兼顾检测器的实际需求。同样，在检测器设计时，一方面要有效利用精细化建模的成果，提升算法对复杂海洋环境的适应性，另一方面又要做出合理简化，以使其满足工程应用的需求。两者之间如何折中考虑，是需要进一步探索的问题。

(3) 海杂波与目标差异特性认知

雷达目标检测问题从本质上看是要有效区分“目标+海杂波”与纯海杂波，因此，研究海杂波与目标差异特性认知更能体现雷达目标检测问题的实质。在考虑扰动反馈机理的情况下，目标的存在对海面具有扰动作用，海面对目标也具有反馈作用。为此，在同时考虑目标对海面的扰动作用和海面对目标的反馈作用前提下，可进一步研究目标扰动作用下距离-方位联合维度海杂波特性、海面反馈作用下半空间目标特性，分别形成海杂波模型和目标模型，在此基础上，寻求可稳定反映目标与海杂波差异的特征，并给出相应的参数估计方法。该差异特性认知是一个新的研究课题，可为海杂波中目标检测技术研究提供技术支持，目前该内容已得到国家自然科学基金项目“扰动反馈作用下雷达目标与海杂波差异特性认知研究”(编号为61401495)的资助。

(4) 海杂波特性认知在海面状态测量中的应用

对雷达探测而言，海杂波是不利因素，海杂波特性认知的主要目的在于抑制海杂波、改善信杂比、提升检测性能。然而，在海洋遥感领域，海杂波信号中包含了丰富的海浪信息，通过对实测海杂波视频图像序列进行分析与处理，可以实现海面状态测量的功能，即海态反演。反演得到的海浪参数主要包括有效波高、谱峰频率、频谱宽度、平均周期等。已有海态反演算法对雷达系统和环境参数均有较高要求，例如，雷达为固定平台，HH极化，脉宽小于80 ns，且风速应大于3 m/s等。能否结合海杂波特性认知所得到的精细化信息改善海态反演算法的适用性，是一个值得关注的问题。

[1]Ward K and Watts S. Use of sea clutter models in radar design and development[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 146–157.

[2]Ward K, Tough R, and Watts S. Sea Clutter: Scattering, the K-distribution and Radar Performance, 2nd ed[M]. London: The Institution of Engineering and Technology, 2013.

[3]Long M W. Radar Reflectivity of Land and Sea, 3nd ed[M]. London: Artech House radar library, 2001.

[4]Skolnik M I. Radar Handbook, 3nd ed[M]. New York: The McGraw-Hill Companies Inc., 2008.

[5]Gini F, Farina A, and Greco M. Selected list of references on radar signal processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 329–359.

[6]Daley J C, Ransone J T, Burkett J A, et al.. Sea clutter measurements on four frequencies[R]. Naval Research Laboratory Report 6806, November 1968.

[7]Titi G W and Marshall D F. The ARPA/Navy Mountaintop program: adaptive signal processing for airborne early warning radar[C]. In Proceedings of 1996 IEEE International Conference on Acoustics, Speech, and Signal Processing, 1996: 1165–1168.

[8]Little M O and Berry W P. Real-time multichannel airborne radar measurements[C]. IEEE National Radar Conference, 1997: 138–142.

[9]Charles L R, Eckert E, Siegel A, et al.. X-band lowgrazing-angle ocean backscatter obtained during LOGAN 1993[J]. IEEE Journal of Oceanic Engineering, 1997, 22(1): 18–26.

[10]Drosopoulos A. Description of the OHGR database[R]. Defence Research Establishment Ottawa, Technical Note 94–14, 1994.

[11]Wind H J De, Cilliers J C, and Herselman P L. Sea clutter and small boat radar reflectivity databases[J]. IEEE Signal Processing Magazine, 2010, 32(2): 145–148.

[12]Hair T, Lee T, and Baker C J. Statistical properties of multifrequency high-range-resolution sea reflections[J]. IEE Proceedings-F, 1991, 138(2): 75–79.

[13]Carretero-Moya J, Gismero-Menoyo J, Blanco-del-Campo A, et al.. Statistical analysis of a high-resolution sea-clutter database[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2024–2037.

[14]Antipov I. Simulation of sea clutter returns[R]. Technical Report, DSTO-TR-0679, 1998.

[15]Antipov I. Analysis of sea clutter data[R]. Technical Report, DSTO-TR-0647, 1998.

[16]Choong P L. Modelling airborne L-band radar sea and coastal land clutter[R]. Technical Report, DSTO-TR-0945, 2000.

[17]Antipov I. Statistical analysis of northern Australian coastline sea clutter data[R]. Technical Report, DSTO-TR-1236, 2002.

[18]Dong Y. Clutter spatial distribution and new approaches of parameter estimation for Weibull and K-distributions[R]. Technical Report, DSTO-RR-0274, 2004.

[19]Dong Y. Distribution of X-band high resolution and high grazing angle sea clutter[R]. Technical Report, DSTO-RR-0316, 2006.

[20]Dong Y. High grazing angle and high resolution sea clutter correlation and polarization analyses[R]. Technical Report, DSTO-TR-1972, 2007.

[21]Dong Y and Merrett D. Statistical measures of S-band sea clutter and targets[R]. Technical Report, DSTO-TR-2221, 2008.

[22]Dong Y and Merrett D. Analysis of L-band multi-channel sea clutter[R]. Technical Report, DSTO-TR-2455, 2010.

[23]Bocquet S. Calculation of radar probability of detection in K-distributed sea clutter and noise[R]. Technical Report, DSTO-TN-1000, 2011.

[24]Weinberg G. Investigation of the Pareto distribution as a model for high grazing angle clutter[R]. Technical Report, DSTO-TR-2525, 2011.

[25]Dong Y, Rosenberg L, and Weinberg G. Generating correlated gamma sequences for sea-clutter simulation[R]. Technical Report, DSTO-TR-2688, 2012.

[26]Rosenberg L and Watts S. High grazing angle sea-clutter literature review[R]. Technical Report, DSTO-GD-0736, 2013.

[27]Whitrow J L. A model of low grazing angle sea clutter for coherent radar performance analysis[R]. Technical Report, DSTO-TR-2864, 2013.

[28]Rosenberg L. Sea-spike detection in high grazing angle X-band sea-clutter[R]. Technical Report, DSTO-TR-2820, 2013.

[29]Ward K D, Barker C J, and Watts S. Maritime surveillance radar Part 1: Radar scattering from the ocean surface[J]. IEE Proceedings-F, 1990, 137(2): 51–63.

[30]Greco M, Gini F, and Rangaswamy M. Statistical analysis of measured polarimetric clutter data at different range resolutions[J]. IEE Proceedings-Radar, Sonar and Navigation, 2006, 153(6): 473–481.

[31]Gregers-Hansen V and Mital R. An improved empirical model for radar sea clutter reflectivity[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3512–3524.

[32]Raynal M A and Doerry A W. Doppler characteristics of sea clutter[R]. Technical Report, SAND2010-3828, 2010.

[33]Watts S. Modeling and simulation of coherent sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3303–3317.

[34]Al-Ashwal W A, Woodbridge K, and Griffiths H D. Analysis of bistatic sea clutter—Part I: Average reflectivity[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1283–1292.

[35]Al-Ashwal W A, Woodbridge K, and Griffiths H D. Analysis of bistatic sea clutter—Part II: Amplitude statistics[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1293–1303.

[36]Gini F and Greco M. Texture modelling, estimation and validation using measured sea clutter data[J]. IEE Proceedings-Radar, Sonar and Navigation, 2002, 149(3): 115–124.

[37]Plant W J. Microwave sea return at moderate to high incidence angles[J]. Waves in Random Media, 2003, 13(4): 339–354.

[38]Gotwols B L, Thompson D R, and Chapman R D. Ocean backscatter distribution functions at mid incidence[C]. Proceedings Engineering in Harmony with Ocean, 1993: II/10.

[39]Greco M, Stinco P, and Gini F. Impact of sea clutter nonstationarity on disturbance covariance matrix estimation and CFAR detector performance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 1502–1513.

[40]Lamont-Smith T, Waseda T, and Rheem C K. Measurements of the Doppler spectra of breaking waves[J]. IET Radar, Sonar & Navigation, 2007, 1(2): 149–157.

[41]Trunk G V and George S F. Detection of targets in non-Gaussian sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1970, 6(5): 620–628.

[42]Trunk G V. Radar properties of non-Rayleigh sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1972, 8(2): 196–204.

[43]Trunk G V. Non-Rayleigh sea clutter: Properties and detection of targets[R]. NRL Report, 1976, No. 7986.

[44]Jakeman E and Pusey P N. A model for non-Rayleigh sea echo[J]. IEEE Transactions on Antennas and Propagation, 1976, 24(6): 806–814.

[45]Sangston K J and Gerlach K R. Coherent detection of radar targets in a non-Gaussian background[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(2): 330–340.

[46]Chan H C. Radar sea-clutter at low grazing angles[J]. IEE Proceedings-F, 1990, 137(2): 102–112.

[47]Stehwien W. Statistics and correlation properties of high resolution X-band sea clutter[C]. Proceedings of the 1994 IEEE National Radar Conference, 1994: 36–51.

[48]Conte E, Maio A De, and Galdi C. Statistical analysis of real clutter at different range resolutions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 903–918.

[49]Haykin S, Bakker R, and Currie B W. Uncovering nonlinear dynamics: The case study of sea clutter[J]. Proceedings of the IEEE, 2002, 90(5): 860–881.

[50]Greco M, Bordoni F, and Gini F. X-band sea-clutter nonstationarity: Influence of long waves[J]. IEEE Journal of Ocean Engineering, 2004, 29(2): 269–283.

[51]Watts S and Wicks D C. Empirical models for prediction in K-distribution radar sea clutter[C]. IEEE International Radar Conference, 1990: 189–194.

[52]Ryan J and Johnson M. Radar performance prediction for target detection at sea[C]. IEE Conference Radar-92, 1992: 13–17.

[53]Conte E, Lops M, and Ricci G. Asymptotically optimum radar detection in compound-Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(2): 617–625.

[54]Conte E, Lops M, and Ricci G. Adaptive matched filter detection in spherically invariant noise[J]. IEEE Signal Processing Letters, 1996, 3(8): 248–250.

[55]Conte E and Maio A D. Mitigation techniques for non-Gaussian sea clutter[J]. IEEE Journal of Ocean Engineering, 2004, 29(2): 284–302.

[56]Pulsone N B and Raghavan R S. Analysis of an adaptive CFAR detector in non-Gaussian interference[J]. IEEETransactions on Aerospace and Electronic Systems, 1999, 35(3): 903–916.

[57]Rangaswamy M. Statistical analysis of the nonhomogeneity detector for non-Gaussian interference backgrounds[J]. IEEE Transactions on Signal Processing, 2005, 53(6): 2101–2111.

[58]Farina A, Gini F, Greco M V, et al.. High resolution sea clutter data: Statistical analysis of recorded live data[J]. IEE Proceedings-Radar, Sonar and Navigation, 1997, 144(3): 121–130.

[59]Shnidman D A. Generalized radar clutter model[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 857–865.

[60]Rosenberg L and Bocquet S. Application of the Pareto plus noise distribution to medium grazing angle sea-clutter[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(1): 255–261.

[61]Liu Y, Frasier S J, and Mcintosh R E. Measurement and classification of low-grazing-angle radar sea spikes[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(1): 27–40.

[62]Gutnik V G, Kulemin G P, and Sharapov L. Spike statistics features of the radar sea clutter in the millimeter wave band at extremely small grazing angles[J]. Physics and Engineering of Millimeter and Sub-Millimeter Waves, 2001, 43(3): 426–428.

[63]Melief H W, Greidanus H, and Genderen P. Analysis of sea spikes in radar sea clutter data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(4): 985–993.

[64]Lyzenga D R, Maffett A L, and Shuchman R A. The contribution of wedge scattering to the radar cross section of the ocean surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 1983, 21(4): 502–505.

[65]Keller M R, Gotwols B L, and Chapman R D. Multiple sea spike definitions: Reducing the clutter[C]. Geoscience and Remote Sensing Symposium, 2002: 940–942.

[66]Posner F and Gerlach K. Sea spike demographics at high range resolutions and very low grazing angles[C]. Radar Conference, Proceedings of the 2003 IEEE, 2003: 38–45.

[67]Posner F L. Spiky sea clutter at high range resolutions and very low grazing angles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 58–73.

[68]Greco M, Stinco P, and Gini F. Identification and analysis of sea radar clutter spikes[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 239–250.

[69]Rosenberg L. Sea-spike detection in high grazing angle X-band sea-clutter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(8): 4556–4562.

[70]Middleton D. New physical-statistical methods and models for clutter and reverberation: The KA-distribution and related probability structures[J]. IEEE Journal of Ocean Engineering, 1999, 24(3): 261–283.

[71]Ward K D and Tough R J. Radar detection performance in sea clutter with discrete spikes[C]. International Conference Radar 2002, 2002: 253–257.

[72]Watts S, Ward K D, and Tough R J A. The physics and modelling of discrete spikes in radar sea clutter[C]. Proceedings of International Radar Conference, 2005: 72–77.

[73]Rosenberg L, Crisp D J, and Stacy N J. Analysis of the KK-distribution with medium grazing angle sea-clutter[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 209–222.

[74]Blunt S D, Gerlach K, and Heyer J. HRR detector for slow-moving targets in sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 965–974.

[75]许心瑜, 张玉石, 黎鑫, 等. L波段小擦地角海杂波KK分布建模[J]. 系统工程与电子技术, 2014, 36(7): 1304–1308. Xu X Y, Zhang Y S, Li X, et al.. KK distribution modeling with L band low grazing sea clutter[J]. Systems Engineering and Electronics, 2014, 36(7): 1304–1308.

[76]高彦钊, 占荣辉, 万建伟. KK分布杂波下的距离扩展目标检测算法[J]. 国防科技大学学报, 2015, 37(1): 118–124. Gao Y Z, Zhan R H, and Wan J W. Range-spread target detection in KK-distributed clutter[J]. Journal of National University of Defense Technology, 2015, 37(1): 118–124.

[77]Ding H, Huang Y, Liu N B, et al.. Modeling of sea spike events with generalized extreme value distribution[C]. Proceedings European Radar Conference (EuRAD), 2015: 113–116.

[78]Balleri A, Nehorai A, and Wang J. Maximum likelihood estimation for compound-Gaussian clutter with inverse gamma texture[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 775–780.

[79]Gotwols B L and Thompson D R. Ocean microwave backscatter distributions[J]. Journal of Geophysical Research, 1994, 99(C5): 9741–9750.

[80]Ollila E, Tyler D E, Koivunen V, et al.. Compound-Gaussian clutter modeling with an inverse Gaussian texture distribution[J]. IEEE Signal Processing Letters, 2012, 19(12): 876–879.

[81]Anastassopoulos V, Lampropoulos G A, and Drosopoulos A. High resolution radar clutter statistics[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 43–60.

[82]Fayard P and Field T R. Inference of a generalised texture for a compound-Gaussian clutter[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 187–194.

[83]Gini F, Greco M, Diani M, et al.. Performance analysis of two adaptive radar detectors against non-Gaussian real seaclutter data[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(4): 1429–1439.

[84]Farshchian M and Posner F L. The Pareto distribution for low grazing angle and high resolution X-band sea clutter[C]. IEEE Radar Conference, 2010: 789–793.

[85]Rosenberg L and Bocquet S. The Pareto distribution for high grazing angle sea-clutter[C]. IEEE International Geoscience and Remote Sensing Symposium, 2013: 4209–4212.

[86]Weinberg G V. Assessing Pareto fit to high-resolution high-grazing-angle sea clutter[J]. Electronics Letters, 2011, 47(8): 516–517.

[87]Rosenberg L, Watts S, and Bocquet S. Application of the K+Rayleigh distribution to high grazing angle seaclutter[C]. International Radar Conference, 2014: 1–6.

[88]Fiche A, Angelliaume S, Rosenberg L, et al.. Analysis of XBand SAR sea-clutter distributions at different grazing angles[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4650–4660.

[89]Hu J, Tung W, and Gao J. A new way to model nonstationary sea clutter[J]. IEEE Signal Processing Letters, 2009, 16(2): 129–132.

[90]Tsihrintzis G A and Nikias C L. Evaluation of fractional, lower-order statistics-based detection algorithms on real radar sea-clutter data[J]. IEE Proceedings-Radar, Sonar and Navigation, 1997, 144(1): 29–37.

[91]石志广, 周剑雄, 付强. K分布海杂波参数估计方法研究[J].信号处理, 2007, 23(3): 420–424. Shi Z G, Zhou J X, and Fu Q. Parameter estimation study of K-distributed sea clutter[J]. Signal Processing, 2007, 23(3): 420–424.

[92]Marier L J. Correlated K-distributed clutter generation for radar detection and track[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(2): 568–580.

[93]Davidson G. Simulation of coherent sea clutter[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 168–177.

[94]Pidgeon V W. Doppler dependence of radar sea return[J]. Journal of Geophysical Research, 1968, 73: 1333–1341.

[95]Lee P, Barter J D, Beach K L, et al.. Power spectral lineshapes of microwave radiation backscattered from sea surfaces at small grazing angle[J]. IEE Proceedings-Radar, Sonar and Navigation, 1995, 142(5): 252–258.

[96]Lamont-Smith T. An empirical model of EM scattering from steepening wave profiles derived from numerical computations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(6): 1447–1454.

[97]Lamont-Smith T. Investigation of the variability of Doppler spectra with radar frequency and grazing angle[J]. IEE Proceedings-Radar, Sonar and Navigation, 2004, 151(5): 291–298.

[98]Lamont-Smith T. Azimuth dependence of Doppler spectra of sea clutter at low grazing angle[J]. IET Radar, Sonar & Navigation, 2008, 2(2): 97–103.

[99]Lamont-Smith T, Mitomi M, Kawamura T, et al.. Electromagnetic scattering from wind blown waves and ripples modulated by longer waves under laboratory conditions[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 265–279.

[100]Lee P, Barter J D, and Lake B M. Lineshape analysis of breaking wave Doppler spectra[J]. IEE Proceedings-Radar, Sonar and Navigation, 1998, 145(2): 135–139.

[101]Walker D. Experimentally motivated model for low grazing angle radar Doppler spectra of the sea surface[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000, 147(3): 114–120.

[102]Walker D. Doppler modelling of radar sea clutter[J]. IEE Proceedings-Radar, Sonar and Navigation, 2001, 148(2): 73–80.

[103]Rosenberg L. Characterization of high grazing angle X-band sea-clutter Doppler spectra[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 406–417.

[104]Rosenberg L and Stacy N J. Analysis of medium grazing angle X-band sea-clutter Doppler spectra[C]. Proceedings of the IEEE Radarcon Conference, 2008: 1–6.

[105]Watts S. The effects of covariance matrix mismatch on adaptive CFAR performance[C]. IEEE Radar 2013 International Conference, 2013: 495–499.

[106]Miller R J. Variability in spectra of low-grazing angle sea clutter returns[R]. NATO/RTO Publications, Proceedings of SET Symposium on Low Grazing Angle Clutter: Its Characterisation, Measurement and Application, 2000.

[107]Ritchie M A, Stove A G, Watts S, et al.. Application of a new sea clutter Doppler model[C]. IEEE Radar 2013 International Conference, 2013: 560–565.

[108]Watts S, Rosenberg L, Bocquet S, et al.. Doppler spectra of medium grazing angle sea clutter Part 1: Characterisation[J]. IET Radar, Sonar & Navigation, 2016, 10(1): 24–31.

[109]Watts S, Rosenberg L, Bocquet S, et al.. Doppler spectra of medium grazing angle sea clutter Part 2: Model assessment and simulation[J]. IET Radar, Sonar & Navigation, 2016, 10(1): 32–42.

[110]Baker C J. K-distributed coherent sea clutter[J]. IEE Proceedings-F, 1991, 138(2): 89–92.

[111]Ritchie M A, Woodbridge K, and Stove A G. Analysis of sea clutter distribution variation with Doppler using the compound K-distribution[C]. IEEE Radar 2010 International Conference, 2010: 495–499.

[112]Ding H, Sun Y L, Liu N B, et al.. Bispectrum property analysis of high resolution real sea clutter[C]. IETInternational Radar Conference, 2015: 1–4.

[113]Haykin S and Thomson D J. Signal detection in a nonstationary environment reformulated as an adaptive pattern classification problem[J]. Proceedings of the IEEE, 1998, 86(11): 2325–2344.

[114]Guan J, Zhang J, and Liu N B. Time-frequency entropy of Hilbert-Huang transformation for detecting weak target in the sea clutter[C]. 2009 IEEE Radar Conference, 2009: 1–5.

[115]张建, 黄勇, 关键, 等. 基于局部Hilbert边际谱隶属度的微弱目标检测算法[J]. 信号处理, 2011, 27(9): 1335–1340. Zhang J, Huang Y, Guan J, et al.. Weak target detection based on the membership degree of partial Hilbert marginal spectrum[J]. Signal Processing, 2011, 27(9): 1335–1340.

[116]Chen X L, Guan J, Bao Z H, et al.. Detection and extraction of target with micro-motion in spiky sea clutter via short-time fractional Fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1002–1018.

[117]Rosenberg L. The effect of temporal correlation with K and KK-distributed sea-clutter[C]. IEEE Radarcon Conference, 2012: 0303–0308.

[118]Siegel A, Ochadlick A, Davis Jr J, et al.. Spatial and temporal correlation of LOGAN-1 high-resolution radar sea clutter data[C]. IEEE International Conference on Geoscience and Remote Sensing Symposium, 1994: 818–821.

[119]Farina A, Gini F, Greco M V, et al.. Improvement factor for real sea-clutter Doppler frequency spectra[J]. IEE Proceedings-Radar, Sonar and Navigation, 1996, 143(5): 341–344.

[120]Watts S. Cell-averaging CFAR gain in spatially correlated K-distributed clutter[J]. IEE Proceedings-Radar, Sonar and Navigation, 1996, 143(5): 321–327.

[121]Raghavan R S. A model for spatially correlated radar clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(2): 268–275.

[122]Lombardo P and Oliver C J. Estimating the correlation properties of K-distributed SAR clutter[J]. IEE Proceedings-Radar, Sonar and Navigation, 1995, 142(4): 167–178.

[123]Watts S and Ward K D. Spatial correlation in K-distributed sea clutter[J]. IEE Proceedings F Communications, Radar and Signal Processing, 1987, 134(6): 526–532.

[124]Armstrong B C and Griffiths H D. Modeling spatially correlated K-distributed clutter[J]. Electronics Letters, 1991, 27(15): 1355–1356.

[125]Armstrong B C and Griffiths H D. CFAR detection of fluctuating targets in spatially correlated K-distributed clutter[J]. IEE Proceedings F-Radar and Signal Processing, 1991, 138(2): 139–152.

[126]Tough R J A, Ward K D, and Shepherd P W. The modelling and exploitation of spatial correlation in spiky sea clutter[C]. EMRS DTC 2nd Annual Conference, 2005: A1.

[127]关键, 丁昊, 黄勇, 等. 实测海杂波数据空间相关性研究[J].电波科学学报, 2012, 27(5): 943–954. Guan J, Ding H, Huang Y, et al.. Spatial correlation property with measured sea clutter data[J]. Chinese Journal of Radio Science, 2012, 27(5): 943–954.

[128]Ding H, Guan J, Liu N B, et al.. New spatial correlation models for sea clutter[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(9): 1833–1837.

[129]何友, 黄勇, 关键, 等. 海杂波中的雷达目标检测技术综述[J].现代雷达, 2014, 36(12): 1–9. He Y, Huang Y, Guan J, et al.. An overview on radar target detection in sea clutter[J]. Modern Radar, 2014, 36(12): 1–9.

[130]Stankovic L, Thayaparan T, and Dakovic M. Signal decomposition by using the S-method with application to the analysis of HF radar signals in sea-clutter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4332–4342.

[131]Dong Y H and Crisp D J. The Euler decomposition and its application to sea clutter analysis[C]. IEEE International Conference on Radar, 2008: 133–138.

[132]Huang N E, Shen Z, Long S R, et al.. The empirical mode decomposition and the Hilbert spectrum for nonlinear and Non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 1998, 454(1971). doi: 10.1098/rspa.1998.0193.

[133]Gini F and Greco M. Texture modelling, estimation and validation using measured sea clutter data[J]. IEE Proceedings-Radar, Sonar and Navigation, 2002, 149(3): 115–124.

[134]Gini F, Giannakis G B, Greco M, et al.. Time-averaged subspace methods for radar clutter texture retrieval[J]. IEEE Transactions on Signal Processing, 2001, 49(9): 1886–1898.

[135]Dinesh R and Jeffrey K. Adaptive radar detection in doubly nonstationary autoregressive Doppler spread clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 484–497.

[136]Carretero-Moya J, Gismero-Menoyo J, Asensio-Lopez A, et al.. Small-target detection in high-resolution heterogeneous sea-clutter: an empirical analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 1880–1898.

[137]Leung H and Lo T. Chaotic radar signal processing over the sea[J]. IEEE Journal of Ocean Engineering, 1993,18(3): 287–295.

[138]Unsworth C P, Cowper M R, Mclaughlin S, et al.. Reexamining the nature of radar sea clutter[J]. IEE Proceedings-Radar, Sonar and Navigation, 2002, 149(3): 105–114.

[139]Mcdonald M and Damini A. Limitations of nonlinear chaotic dynamics in predicting sea clutter returns[J]. IEE Proceedings-Radar, Sonar and Navigation, 2004, 151(2): 105–113.

[140]Blu T and Unser M. Self-similarity: Part II—Optimal estimation of fractal processes[J]. IEEE Transactions on Signal Processing, 2007, 55(4): 1364–1378.

[141]Hu J, Tung W W, and Gao J B. Detection of low observable targets within sea clutter by structure function based multifractal analysis[J]. IEEE Transactions on Antenna and Propagation, 2006, 54(1): 136–143.

[142]Hu J, Gao J B, Posner F L, et al.. Target detection within sea clutter: A comparative study by fractal scaling analyses[J]. Fractals, 2006, 14(3): 187–204.

[143]Peng C K, Buldyrev S V, Goldberger A L, et al.. Statistical properties of DNA sequences[J]. Physica A, 1995, 221(1/3): 180–192.

[144]Kantelhardt J W, Koscielny-Bunde E, Rego H H A, et al.. Detecting long range correlations with detrended fluctuation analysis[J]. Physica A, 2001, 295(3/4): 441–454.

[145]Bashan A, Bartsch R, Kantelhardt J W, et al.. Comparison of detrending methods for fluctuation analysis[J]. Physica A, 2008, 387(21): 5080–5090.

[146]Xu X K. Low observable targets detection by joint fractal properties of sea clutter: An experimental study of IPIX OHGR datasets[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(4): 1425–1429.

[147]许小可. 基于非线性分析的海杂波处理与目标检测[D]. [博士论文], 大连海事大学, 2008. Xu X K. Sea clutter processing and target detecting based on nonlinear analysis[D]. [Ph.D. dissertation], Dalian Maritime University, 2008.

[148]丁昊, 关键, 黄勇, 等. 非平稳海杂波的消除趋势波动分析[J].电波科学学报, 2013, 28(1): 116–123. Ding H, Guan J, Huang Y, et al.. Detrended fluctuation analysis of non-stationary sea clutter[J]. Chinese Journal of Radio Science, 2013, 28(1): 116–123.

[149]Ding H, Wang G Q, and Guan J. Analysis of sea clutter fractal property and target detection based on fit error[C]. Asia-Pacific Conference on Antennas and Propagation Conference, 2012.

[150]Guan J, Liu N B, Zhang J, et al.. Multifractal correlation characteristic for radar detecting low-observable target in sea clutter[J]. Signal Processing, 2010, 90(2): 523–535.

[151]Liu N B, Ding H, Xue Y H, et al.. Approximate fractality of sea clutter fractional Fourier transform spectrum[C]. Proceedings European Radar Conference (EuRAD), 2015: 117–120.

[152]Guan J, Liu N B, Huang Y, et al.. Fractal characteristic in frequency domain for target detection within sea clutter[J]. IET Radar, Sonar & Navigation, 2012, 6(5): 293–306.

[153]刘宁波, 关键, 黄勇, 等. 基于海杂波频谱多尺度Hurst指数的目标检测方法[J]. 电子学报, 2013, 41(3): 424–431. Liu N B, Guan J, Huang Y, et al.. Target detection within sea clutter based on multi-scale Hurst exponent in frequency domain[J]. Acta Electronica Sinica, 2013, 41(3): 424–431.

[154]刘宁波, 关键, 王国庆, 等. 基于海杂波FRFT谱多尺度Hurst指数的目标检测方法[J]. 电子学报, 2013, 41(9): 1847–1853. Liu N B, Guan J, Wang G Q, et al.. Target detection within sea clutter based on multi-scale Hurst exponent in FRFT domain[J]. Acta Electronica Sinica, 2013, 41(9): 1847–1853.

[155]刘宁波, 黄勇, 关键, 等. 实测海杂波频域分形特性分析[J].电子与信息学报, 2012, 34(4): 929–935. Liu N B, Huang Y, Guan J, et al.. Fractal analysis of real sea clutter in frequency domain[J]. Journal of Electronics & Information Technology, 2012, 34(4): 929–935.

Overview and Prospects of Research on Sea Clutter Property Cognition

Ding Hao Dong Yunlong Liu Ningbo Wang Guoqing Guan Jian
(Department of Electronic and Information Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)

Sea clutter is one of the main limiting factors influencing the target detection performance of nautical radars. The physical mechanism of sea clutter is complex with an abundance of influencing factors, and the non-Gaussian as well as non-stationarity behavior is significant. Thus, research into sea clutter property cognition is complicated and has to be systematic. Based on research that concentrates on experimental data, this paper reviews and summarizes the research developments in sea clutter property cognition. It concentrates on the properties that are of most interest for target detection algorithms: amplitude distribution, spectra, correlation, and non-stationarity and nonlinearity. The main research results are also concluded. Based on this, four aspects of problems that need further exploration are highlighted and include the following: further analysis of sea clutter influencing factors; the game problem between sea clutter precision modeling and the requirements of detection algorithms; and the property cognition between radar target and sea clutter.

Sea clutter; Property cognition; Non-Gaussian; Non-stationarity; Precision modeling; Target detection

TN959

2095-283X(2016)05-0499-18

10.12000/JR16069

丁昊, 董云龙, 刘宁波, 等. 海杂波特性认知研究进展与展望[J]. 雷达学报, 2016, 5(5): 499–516.

10.12000/JR16069.

Reference format: Ding Hao, Dong Yunlong, Liu Ningbo, et al.. Overview and prospects of research on sea clutter property cognition[J]. Journal of Radars, 2016, 5(5): 499–516. DOI: 10.12000/JR16069.