Aclass of extended ishikawa iterative processes in Banachspaces for nonexpansive mappings
2016-11-30,
,
(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang, 110034, China)
Aclass of extended ishikawa iterative processes in Banachspaces for nonexpansive mappings
CHENGCongdian,GUANHongyan
(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang, 110034, China)
The problem whether a iterative process of nonexpansive mappingTin real Banach Spaces converges to its fixed point(IPNMCFP)has be extensively studied. Particularly, in 2004, Xu H K constructed a kind of extended Mann iterative process for nonexpansive mapping T, and by the so called viscosity approximation methods, he proved that the iterative process converges strongly to a fixed point of Tunder the uniformly smooth Banach Spaces. In 2007, Zhang S S developed the work of Xu H K. This paper further studies the problem IPNMCFP. By replacing constants with operators, the Ishikawa iterative process is generalized as a class of extended Ishikowa iterative process. Under some conditions, the strong convergence of the iterative process is proved in the viscosity approximation methods, using the theory of duality mapping and variational inequality. And in a special case the iterative process converges strongly to a fixed point ofTis also proved. For the introduced iterative process involves many kinds of Mann and Ishikawa iterative processes, the main conclusion of the present work extends and generalizes some recent results of this research area.
nonexpansive mapping; fixed point; sequence; Mann iterative process; Ishikawa iterative process
0 Introduction and preliminaries
Throughout the present work, we always assume thatEis a real Banach space,E*is the duality space of E, 〈·,·〉 is the dual pair betweenEandE*, andJ:E→2E*is the normalized duality mapping defined by
(1)
We also assume thatDis a nonempty closed convex subset ofE,T:D→Dis a mapping, andF(T) denotes the set of all the fixed points ofT. In addition, we useΠDrepresenting all the contractions onD, i.e.ΠD={f|f:D→D, and there existsα∈(0,1) such that ‖f(x)-f(y)‖≤α‖x-y‖ for allx,y∈D}.

The following result is well known (see Goebel and Reich[1]).
Proposition Let E be uniformly smooth. Then the duality mappingJdefined by (1) is single valued, and it is uniformly continuous on the bounded subset ofEwith the norm topologies ofEandE*.
Recall that the sequences
(2)
(3)
(4)
(5)
are respectively called Mann iterative process, Ishikawa iterative process, modified Mann iterative process with error and modified Ishikawa iterative process with error ofT, wherex0,u∈Dandn≥0. The problem for these iterative sequences converging to the fixed point ofTwas studied by lots of authors, e.g., Halpern[2], Reich[3], Zhang and Tian[4], Chidume[5], Liu[6], Liu Q H and Liu Y[7], Zhao and Zhang[8]. In particular, Xu[9]generalized (2) to the iterative process
(6)
Under a certain conditions, he proved that {xn} converges strongly to a fixed point ofTand other related results. In 2007, Zhang[10]extended and improved the work of Xu.
Motivated and inspired by the contributions above, the present work addresses the following iterative process.
(7)
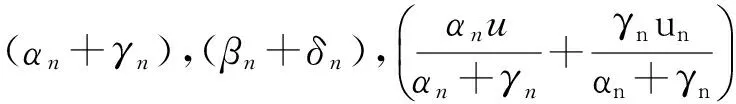
Lemma 1[9]LetXbe a uniformly smooth Banach space,Cbe a closed convex subset ofX,T:C→Cbe a nonexpansive withF(T)≠φ, andf∈ΠC. Then {xt} defined byxt=tf(xt)+(1-t)Txtconverges strongly to a point inF(T). If we defineQ:ΠC→F(T) by
(8)
thenQ(f) solves the variational inequality
In particular, iff=u∈Cis a constant, then (8) is reduced to the sunny nonexpansive retraction of Reich fromContoF(T),

Lemma 2[11]LetXbe a real Banach space andJp:X→2X*,1 Lemma 3[6]Let {an},{bn} and {cn} be three nonnegative real sequences satisfying In this section, we address the strong convergence of the iterative sequence (7). Lemma 4 Letf,fn∈ΠD,tn∈(0,1), letTbe a nonexpansive mapping, and letznbe the unique solution of the equationz=tnfn(z)+(1-tn)Tzfor alln≥0. Thenzn→Q(f)(defined by (8) ) astn→0 (strongly) if {fn(x)} converges uniformly tof(x) onD. This leads to Proof Since ‖Txn-xn‖→0, we can choose {tn} such that ‖Txn-xn‖=o(tn). Letznbe the unique solution of the fixed point of equationz=tnfn(z)+(1-tn)Tz. Then {zn} converges strongly toQ(f) by Lemma 4. Letz=Q(f). Then we have (9) (10) On the other hand, we have (11) (12) (Note:zn→zand {xn} is bounded.) and Substitute in (11) the (12), (13) and (14), we obtain (15) (Note: In terms of Proposition 1,jis uniformly continuous on bounded subset.) Combining (10), (11) and (15), we also obtain This further leads to By Lemma 2,xn+1→z. This completes the proof. Whenβn=1,gn(x)=xandfn(x)=f(x), (7) reduces to (6), and that {fn(x)} converges uniformly tofholds obviously. By Theorem 1, we can immediately obtain the following conclusion, which is the major conclusion of [10, Theorem 1]. In addition,Yao[12]also studied the sequence (16) which can be transformed as Thus, we can easily know the following conclusion holds from Theorem 1, which can be taken as a complementary result of [12, Theorem 3.1]. A class of extended Ishikowa iterative process for a nonexpansive mappingTin real Banach Spaces, which involves many kinds of Mann and Ishikawa iterative processes, is introduced and studied. Under some conditions, the strong convergence of the iterative process is proved by the viscosity approximation methods. And in a special case, the iterative process converges strongly to a fixed point ofTis also proved. The main conclusion of the present work extends and generalizes some recent results of this research area. [ 1 ]GOEBEL K, REICH S. Uniform convexity nonexpansive mappings and hyperbolic geometry [J]. M Dekker, 1984. [ 2 ]HALPERN B. Fixed points of nonexpansive maps[J]. Bull Amer Math Soc, 1967,73(6):957-961. [ 3 ]REICH S. Weak convergence theorems for nonexpansive mappings in Banach spaces[J]. J Math Anal Appl, 1979,67(2):274-276. [ 4 ]ZHANG S S, TIAN Y X. On Halpern’s open question [J]. Acta Mathematica Sinica, Chinese Series, 2005,48(5):979-984. [ 5 ]CHIDUME C E. Approximation of fixed points of strongly pseudocontractive mappings[J]. Proc Amer Math Soc, 1994,120(2):545-551. [ 6 ]LIU L S. Ishikawa and Mann iterative processes with errors for nonlinear strongly Accretive mappings in Banach spaces[J]. J Math Anal Appl, 1995,194(1):114-125. [ 7 ]LIU Q H, LIU Y. Ishikawa iterative sequences for hemi-contractive mappings with error member[J]. Acta Mathematica Sinica, Chinese series, 2006,49(6):1213-1216. [ 8 ]ZHAO L C, ZHANG S S. Strong convergence theorem for asymptotically nonexpansive mappings with errors in Banach spaces[J]. Acta Mathematica Sinica, Chinese Series, 2008,51(1):99-108. [ 9 ]XU H K. Viscosity approximation methods for nonexpansive mappings[J]. J Math Anal Appl, 2004,298(1):279-291. [10]ZHANG S S. Viscosity approximation methods for nonexpansive mappings in Banach spaces[J]. Acta mathematica sinica, Chinese Series, 2007,50(3):485-492. [11]ZHANG S S. Some problems and results in the study of nonlinear analysis[J]. Nonliear Anal TMA, 1997,30(7):4197-4208. [12]YAO Y H, CHEN R D , ZHOU H Y. Iterative algorithms to fixed point of nonexpansive mapping[J]. Acta mathematica sinica, Chinese Series, 2007,50(1):139-144. [13]ZHANG S S, YANG L, LIU J A. Strong convergence theorems for nonexpansive semi-groups in Banach spaces[J]. Applied Mathematics and Mechanics (English Edition), 2007,28(10):1287-1297. [14]ZHANG S S, LI X R, CHEN Z J. On the problem of nearest common fixed point of nonexpansive mappings[J]. Acta mathematica sinica, Chinese Series, 2006,49(6):1297-1302. [15]ZHAO L C, ZHANG S S. A viscosity approximation method for generalized equilibrium problems and fixed point problems[J]. Acta Mathematicae Applicatae Sinica, Chinese Series, 2012,35(2):330-345. 1673-5862(2016)02-0201-05 关于巴拿赫空间中非膨胀映射的一类扩展的石川迭代序列 程丛电, 关洪岩 (沈阳师范大学 数学与系统科学学院, 沈阳 110034) 关于巴拿赫空间中非膨胀映射的迭代序列是否收敛到该映射的不动点问题已有许多研究工作;2004年,徐洪坤建立了一种扩展的曼恩迭代序列,并用黏性逼近方法在一致光滑巴拿赫空间的框架下证明了其收敛到该映射的不动点;2007年,张石生推广与改进了徐洪坤的工作。基于以往有关工作,进一步探讨巴拿赫空间中非膨胀映射的迭代序列的收敛性与非膨胀映射的不动点问题。利用算子替换常数值与向量给出了一类扩展的石川迭代序列;基于对偶映射与变分不等式理论,采用黏性逼近方法,证明了该迭代序列的某种强收敛性及一个有关不动点定理。由于所建立的迭代序列概括了多种类型的曼恩和石川迭代序列,此项工作发展与推广了该领域的许多近期研究成果。 非膨胀映射; 序列; 曼恩(Mann)迭代; 石川(Ishikawa)迭代; 不动点 O177 Document code: A 10.3969/ j.issn.1673-5862.2016.02.016 理论与应用研究
1 Main results



2 Special cases

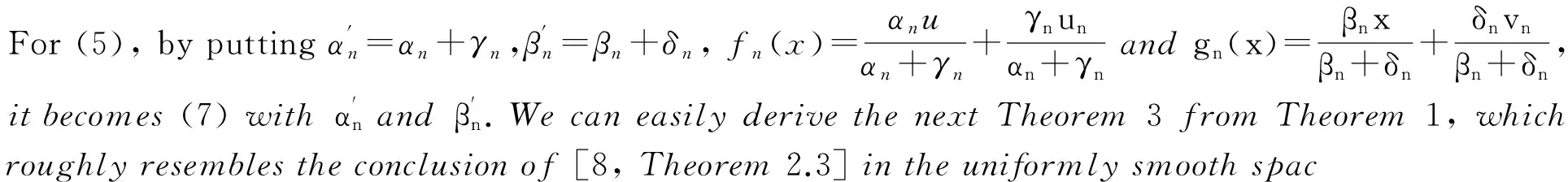

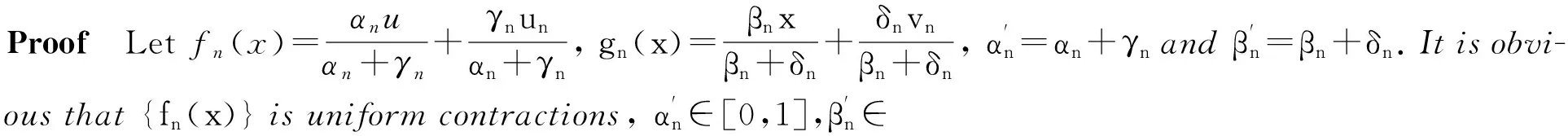


3 Conclusion
