一类非线性泛函积分方程解的存在性*

张 峰

(菏泽学院初等教育系, 山东菏泽 274015)



一类非线性泛函积分方程解的存在性*

张 峰

(菏泽学院初等教育系, 山东菏泽 274015)

应用非紧性测度和 Darbo不动点定理在更弱的条件下研究一类一般化的非线性泛函积分方程解的存在性，推广了一些现有结果.

非线性泛函积分方程；非紧性测度； Darbo不动点定理；存在性

引言

非线性泛函积分方程在解决机械学、物理学、工程技术、生物学等领域频繁出现的问题中有广泛应用[1-4]. 值得提及的是车辆交通理论, 生物和排队理论中出现的一些问题可抽象成非线性积分方程[1]

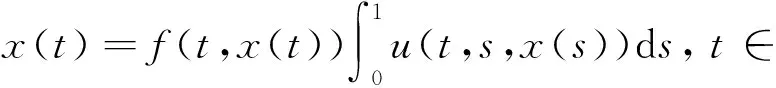
文献[4,5]分别应用非紧性测度和Darbo不动点定理研究了下列非线性积分方程解的存在性，

(1)

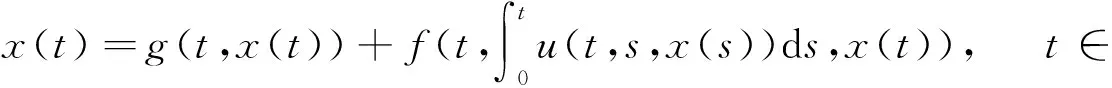
(2)

文献[5]对方程(2)有假设：

(H1)g:[0,a]×R→R和f:[0,a]×R×R→R都是连续函数;

(H2) 存在连续函数a1,a2,a3:[0,a]→[0,a]满足

|g(t,x1)-g(t,x2)|≤a1(t)|x1-x2|, |f(t,y1,x)-f(t,y2,x)|≤a2(t)|y1-y2|,

|f(t,y,x1)-f(t,y,x2)|≤a3(t)|x1-x2|.

受上述文献的启发, 本文考虑一类更一般化的非线性泛函积分方程

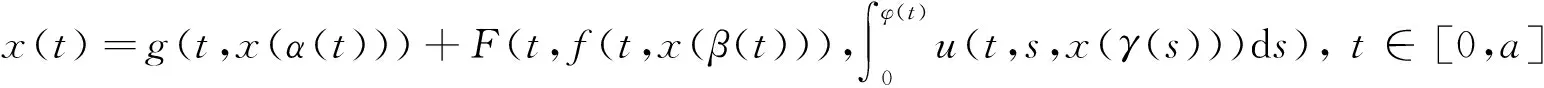
(3)

应用非紧性测度和Darbo不动点定理探讨方程(3)解的存在性.

1 预备知识

设E为实Banach空间, 范数‖·‖及θ为零元素. 记B(x,r)为以x为半径, r为圆心的闭球, Br为球B(θ,r). 记ME为E的所有非空有界集组成的族及NE为ME中所有相对紧集组成的子族. 在主要结果的证明中, 需要下述概念和引理.

定义1.1[6,7]设X∈ME，t∈[0,a]，diamX(t)=sup{|x(t)-y(t)|:x,y∈X}，定义

显然 0≤μ(X)<∞， 称μ(X) 为Kuratowski非紧性测度.

设Ω∈ME, 算子Q:Ω→E连续有界，令μ(X)为E中Kuratowski非紧性测度.若存在常数k∈[0,1)，使得对任意X⊂Ω，都满足 μ(QX)≤kμ(X), 则称Q是Ω上的严格集压缩映射.

引理1.1[6,7](Darbo不动点定理)设Ω为E中非空有界闭凸集，若Q:Ω→Ω是严格集压缩映射,则Q 在Ω中至少有一个不动点.

研究问题的空间为在区间 [0,a] 上所有连续实函数所组成的Banach空间C[0,a]，范数为‖x‖=sup{|x(t)|:t∈[0,a]}. 对于任一固定子集X∈MC[0,a], ε>0 和x∈X，定义

ω(x,ε)=sup{|x(t)-x(s)|:t,s∈[0,a],

|t-s|≤ε},ω(X,ε)=sup{ω(x,ε):x∈X},

(4)

可证明函数ω0(X)是空间C[0,a] 中一Kuratowski 非紧性测度[7].

2 主要结果

作如下假设

(C1) 函数α, β, γ:[0, a]→R,φ:[0, a]→R+连续.

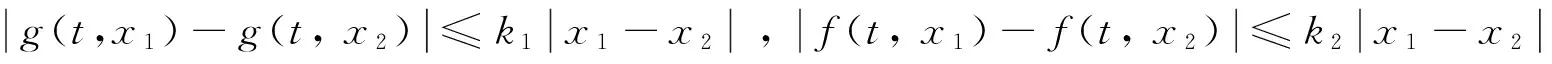
(C3) 函数 u(t, s, x):[0, a]×[0, m]×R→R连续且满足次线性条件, 即对 ∀ t∈[0, a],

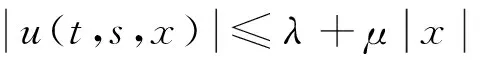
(C4)函数F:[0, a]×R2→R连续且存在常数p, q∈R+,对∀ f1, f2, h1, h2∈R, t∈[0, a]满足

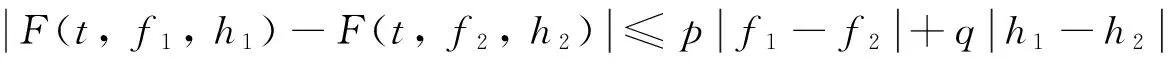
(C5) k1+pk2+qmμ<1.

注： 由条件(C1)知, 存在m∈R+满足φ(t)≤m.

定理2.1 若条件(C1)～(C5)成立, 则积分方程(3)至少有一个解 x∈C[0, a].

证明 首先, 在空间C[0, a]中定义算子Q，

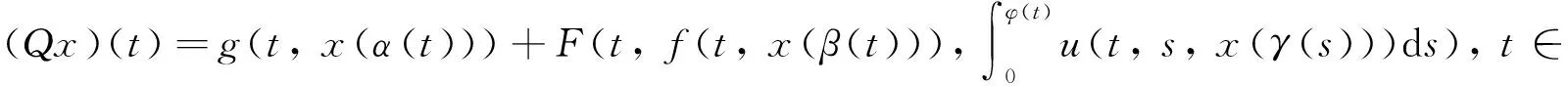
则由条件(C2)和 (C4) 知, 对任意函数x∈C[0, a], 函数Qx在区间 [0, a] 上连续.

其次, 取任意固定x∈C[0, a], 对∀ t∈[0, a] 有

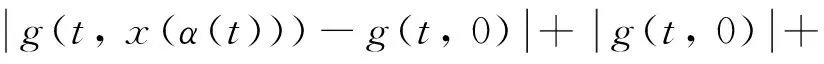
(k1+pk2+qmμ)‖x‖+g0+pf0+qmλ+F0,

(5)

接着,证明算子Q在球Br上连续.对固定的ε>0 及取x, y∈Br, 使得‖x-y‖≤ε, 则对∀t∈[0, a]有

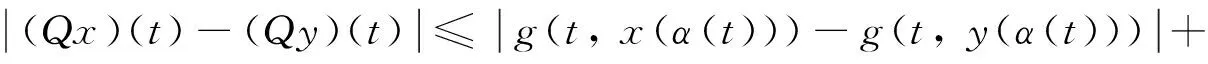
(6)

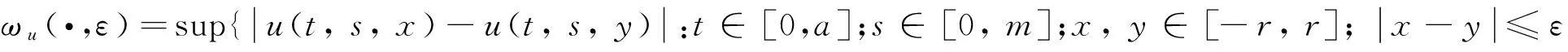
由函数u(t, s, x)在集合 [0,a]×[0, m]×[-r, r]上一致连续知，当ε→0 时, ωu(·,ε)→0. 故由式 (6) 知, 算子Q在球Br上连续.

现在证明算子Q在球Br中相对于式(4)定义的非紧性测度ω0满足Darbo条件.任取Br中非空子集X及x∈X,则对任意固定ε>0及t1, t2∈[0, a],为不失一般性, 设t1≤ t2和 t2-t1≤ε有

|(Qx)(t2)-(Qx)(t1)|≤|g(t2, x(α(t2)))-g(t1, x(α(t1)))| +

|g(t2, x(α(t2)))-g(t1, x(α(t2)))|+|g(t1, x(α(t2)))-g(t1, x(α(t1)))|+

ω(g, ε)+k1|x(α(t2))- x(α(t1))|+pk2|x(β(t2))-x(β(t1))|+pω(f, ε)+

ω(g, ε)+k1ω(x, ω(α,ε))+pk2ω(x,ω(β,ε))+pω(f,ε)+

qmω(u,ε)+qω(φ,ε)(λ+μ|x|) +ω(F, ε)

(7)

式中：

ω(g, ε) =sup{|g(t2, x) - g(t1, x)|: t1, t2∈[0, a]; |t2-t1|≤ε; x∈[-r, r]},

ω(f,ε) = sup{|f(t2, x) - f(t1, x)|: t1, t2∈[0, a]; |t2-t1|≤ε; x∈[-r, r]},

ω(u,ε)=sup{|u(t2, s, x) - u(t1, s, x)|: t1, t2∈[0,a]; s∈[0, m]; |t2-t1|≤ε; x∈[-r, r]},

ω(F, ε) = sup{|F(t2, f, h) - v(t1, f, h)|: t1, t2∈[0, a]; |t2-t1|≤ε;

f∈[- (k2r + f0), k2r + f0]; h∈[- m(λ+μ r), m(λ+μ r)]}.

由式(7)得:

ω(QX,ε)≤ω(g, ε)+(k1+pk2)ω(X, ε) + pω(f, ε) + qmω(u, ε)+

qω(φ, ε)(λ+μ|x|) + ω(F, ε).

(8)

由假设知函数g(t, x), f(t, x)在集合[0, a]×[-r, r],函数u(t, s, x) 在[0, a]×[0, m]×[-r, r]及函数F(t,f,h)在 [0, a]×[-(k2r+f0), k2r+f0]×[-m(λ+μ r),m(λ+μ r)]上一致连续,故由式(8)得:

ω0(QX)≤(k1+pk2)ω0(X)

(9)

由式(9)知算子Q相对于测度ω0在球Br上满足Darbo条件.再由条件(C5)知算子Q相对于测度ω0在球Br上是严格集压缩的. 故应用引理1.1 知算子Q在球Br中至少有一个解. 因此, 方程 (3)在球Br中至少有一个解.

注: 在方程(3)中, 若 φ(t)=t, x=g+F(t, f, h)=fh 即为方程(1).若在方程(3)中α(t)=t,φ(t)=t,f(t, x(β(t))=x(t), x=g+F(t, f, h)=g+F(t, h, x) 即为方程(2) . 再由引言中(H1)和(H2)知, 存在k1, p, q∈R+使得我们的条件(C2)和(C4)成立, 故(C2)和(C4)是较文献[5]中(H1)和(H2)更弱的Lipschitz条件. 故定理 2.1 推广了文 [4,5] 的结果.

3 例子

考虑非线性泛函积分方程

(10)

若记

(11)

则方程(10)为方程(3)的特例. 下面验证方程 (10)满足定理2.1的条件.

首先,由式(11)知

|g(t,x)-g(t, y)|≤k1|x-y|，f(t, x) - f(t, y)|≤k2|x-y|,

|u(t,s, x)|≤λ+μ|x|,

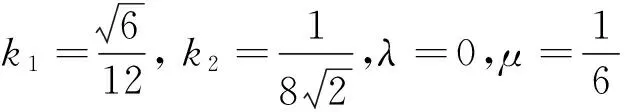
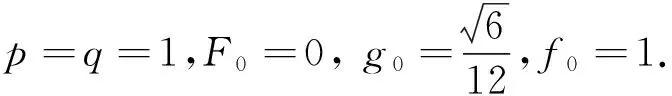
最后, 由定理 2.1 知积分方程 (10) 至少有一个解 x∈C[0, 1].

[1]K.Deimling. Nonlinear Functional Analysis[M]. Berlin: Springer-Verlag, 1985.

[2]M.A.Abdou. On the solution of linear and nonlinear integral equation[J]. Appl.Math.Comput., 2003, 146(2):857-871.

[3]J.Banas, B.Rzepka. On local attractivity and asymptotic stability of solutions of a quadratic Volterra integral equation[J]. Appl.Math.Comput., 2009, 213(1):102-111.

[4]K.Maleknejad, K.Nouri, R.Mollapourasl. Investigation on the existence of solutions for some nonlinear functional integral equations[J]. Nonlinear Anal., 2009, 71(12): e1575-e1578.

[5]K.Maleknejad, K.Nouri, R.Mollapourasl. Existence of solutions for some nonlinear integral equations[J]. Commun.Nonlinear.Sci.Numer.Simulat., 2009, 14(6): 2559-2564.

[6]D.Guo, V.Lakshmikantham, X.Z.Liu. Nonlinear Integral Equations in Abstract Spaces[M]. Kluwer Academic Pub., 1996.

[7]J.Banas, K.Goebel. Measures of Noncompactness in Banach Spaces[M]. New York, Basel:Marcel Dekker, 1980.

Existence of Solutions For a Class of Nonlinear Functional Integral Equations

ZHANG Feng

(Department of Elementary Education, Heze University, Heze Shandong 274015, PRC China)

By using measure of noncompactness and Darbo fixed point theorem, we prove the existence of solutions for a class of more general nonlinear functional integral equations under weaker condition. The result presented in this paper generalizes several ones obtained previously.

nonlinear functional integral equation; measure of noncompactness; Darbo fixed point theorem; existence

1673-2103(2016)05-0024-04

2016-04-20

张峰(1985-)，男，山东曹县人，助教，硕士，研究方向：非线性分析及应用.

O175.5

A