变点方法在多项分布数据中的应用*
2016-11-30白艳丽訾雪旻
白艳丽,訾雪旻
(天津职业技术师范大学理学院,天津 300222)
变点方法在多项分布数据中的应用*
白艳丽,訾雪旻
(天津职业技术师范大学理学院,天津 300222)
利用变点方法,建立了基于多项分布数据这种复杂数据的监控模型,通过数值模拟,验证了检验统计量的优良性,所做变点模型能够准确地找到变点的位置及变点估计值,为更多的实际应用提供有力依据.
多项分布数据;变点方法;渐近正态;同质检验
1 问题描述
当对生产过程进行控制时,需要对产品数据进行收集分析,当统计过程可控时,数据的数值特征就会服从于统计学上某个稳定的分布,如正态分布,二项分布等,相反的,当统计过程失控时,数据分布必然会发生一定的变化,当检测到此变化并报停生产,就可以达到控制产品质量的目的.在统计质量控制中,变点理论有着非常广泛的应用,将变点方法用于不同的数据类型时,对不同的数据特征进行分析,当数据出现异常,其数据分布参数发生相应的变化,这样就可以将变点位置以及变点值估计出来,从而控制质量.本文将变点方法应用于多项分布数据类型,研究得到适合它的变点监控模型.

接下来,需要构造基于多项分布数据的变点模型,假设数据产生的概率发生变化,那么变点模型如下:
(1)
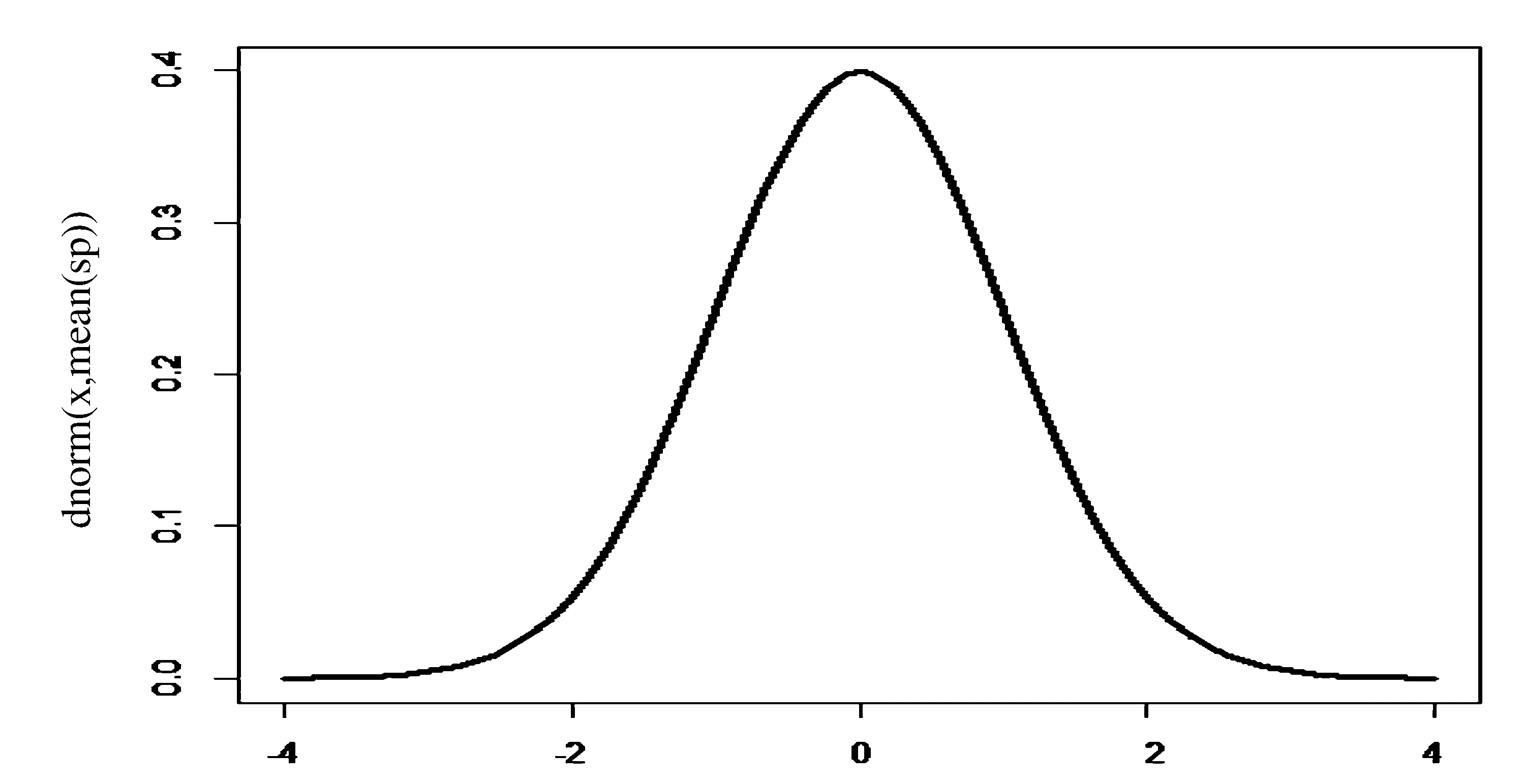
这里τ0>0,很显然,它是两个样本出现差异的分界点,也就是要研究的一个未知的变点,其中qs=(qs1,…,qsp)T,s=0,1.想要检验是否真的存在变点,就相当于在做一个检验问题,将零假设与备择假设记作:H0:τ0=T,H1:τ0 如上所述,变点检验问题与同质检验有相似之处,对于同质检验来说,更有效的方法是二分法和经典的卡方检验的方法,先构造关于两个多项样本Z1τ和Z2τ的同质检验的皮尔森卡方检验统计量,如下: (2) (3) 式(3)中Z1τ,j和Z2τ,j分别是Z1τ和Z2τ的j阶成份,Lτ是从K2中移出来的分量式,这样,所定义的Lτ就可以总是被很好用于研究.另外在检验过程中有可能出现很多的变点,那么为了达到检验目的,应该复查所有可能的变点,因此定义了新的检验统计量Sp, (4) 这里0 对于所构造的统计量Sp的渐近行为,做以下的假设: (A1)当p→∞ 时,max1≤j≤pqoj→0; (A2)当p,N→∞,0 根据假设的成立可以得到以下的结论: (i)假设H0和(A1),(A2)成立时,当p,N→∞时,Sp的期望和方差如下: 这里ΔT=[b(T-1)]-[a(T-1)]+1. (ii)假设(A3)成立,当p,N→∞时 证明如下. 证明(i) 可以将Lτ写成(5)式的形式: (5) 这样,在零假设下将Lτ改写下式(6)的形式: (6) 因此,就可以得到 (7) (8) 在假设(A2)下: 在假设(A1)下,var[Sp,2]/var[Sp,1]→0,最终得到 (9) 证明(ii) (10) 并且存在γ∈(0,∞),使得 (11) 因此可以得到,当p,N→∞时, (12) 我们先来证明(12)式,记El-1(·)=E[·|FN,l-1],有: 因此可以看到: 也就是说γ=1/4, (13) (14) 通常,可以写成如下(15)式形式: (15) 式中: 由假设(A1)和(A2)和一范数的概念可知: 在假设(A3)下,可以得到: 同理B3=o(1).至此(11)式证明完毕. (16) 应用证明(12)式相似的方法在(10)式的证明中,可以得到: 表1 p=1 000,N=1 000,T=100时,数值 根据以上产生的数据,利用统计软件R画出其密度函数图像,如图1所示. X 下面建立常规的控制图,将数据中的变点一一找到,控制图如图2所示: X 从图2可以看出所得到的100个数据中有12个超出了控制线,分别是第33,37,38,55,59,70,76,78,80,85,98,100个.并且返回到变点的估计值分为9 574.480,9 560.900,9 571.593,9 617.917,9 576.615,8 625.516,8 744.992,8 754.763,8 670.260,8 718.625,9 544.144,9 712.753. 本文针对于一种实际生产出现最多但研究却很少的多项分布数据,将变点模型与数据特征值很好的结合起来,构造优良统计量并用统计软件编写相应的统计程序通过数据模拟,验证了该方法的正确性与稳健性. [1]王毓芳,肖诗唐.统计过程控制的策划与实施[M].北京:中国经济出版社,2006:70-71. [2]徐会作.质量控制图经济设计研究[D]. 上海:华东师范大学,2008. [3]吴喜之.复杂数据统计方法-基于R的应用[M].北京:中国人民大学出版社,2012:176-183. [4]肖枝洪,朱强.统计模拟及其R实现[M].武汉:武汉大学出版社,2010:83-88. [5]Shewhart,W.A..The application of statistics as an aid in maintaining Quality of a manufactured production[J].JASA,1925,20:546-548. [6]Robert,S.W..Control Chart Test Based on Geometric Moving Averages[J]. Technometrics,1959,1(3):239-250. [9]谭长春.变点问题的统计推断及其在金融中的应用[D].合肥:中国科学技术大学,2007. [10]朱婴子.统计过程控制在流程化工生产中的应用[D].南京:南京理工大学,2003. [11]Hunter,J.S..The exponentially weighted moving average[J].Joumal of Quality Technology,1986,18:239-250. Application of Change Point Method in the Multinomial Distribution Data BAI Yan-li, ZI Xue-min (School of Science, Tianjin University of Technology and Education,Tianjin 300222, China) This paper uses the change point method to establish the monitoring model of the complex data based on the multinomial distribution data. Through the numerical simulation, it is proved that the test statistic is excellent. The change point model can accurately find the position of the change point and the estimate of the change point, which can provide a strong basis for more practical application. multinomial distribution data; change point method; asymptotic normality; homogeneity test 1673-2103(2016)05-0011-07 2016-04-20 国家自然科学基金面上项目(11271205) 白艳丽(1990-),女,山西晋中人,硕士研究生,研究方向:统计过程控制. 訾雪旻(1977-),女,安徽亳州人,教授,博士,研究方向:统计过程控制. O213.1 A
2 构造检验统计量
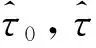
3 统计量的渐近行为
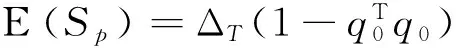
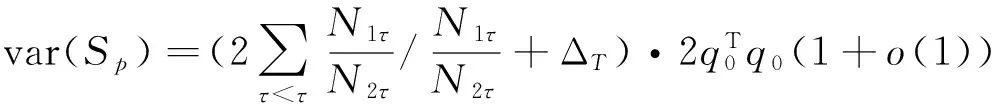

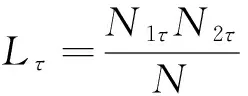
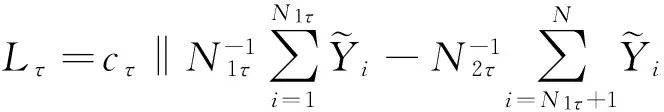

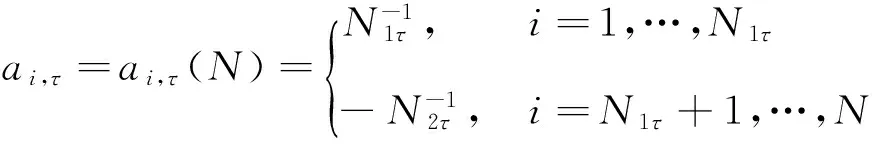

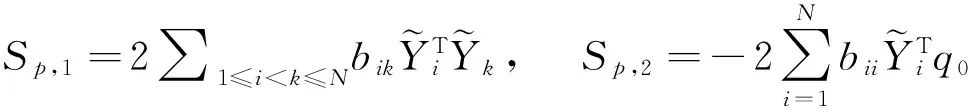

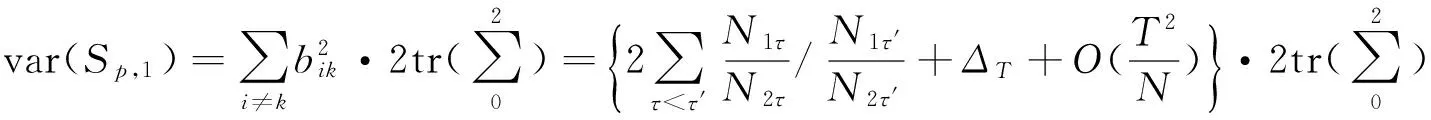

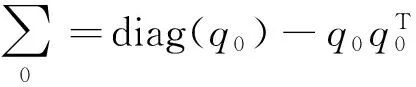

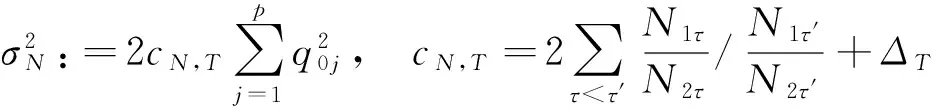

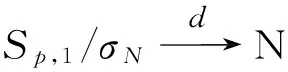

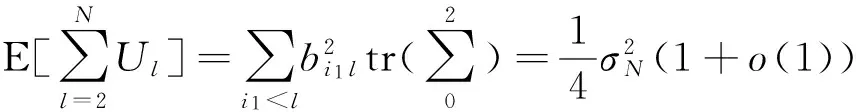

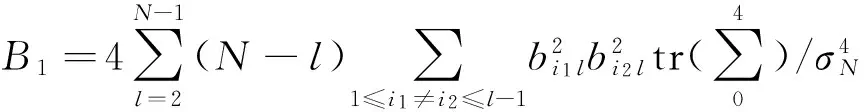
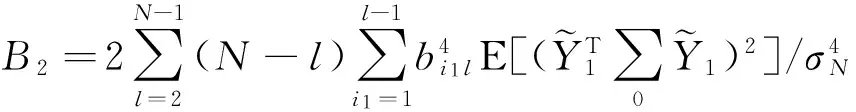

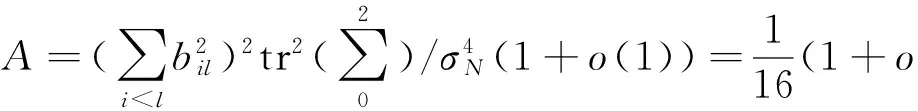


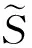
4 数据模拟
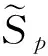
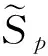


5 结束语
