初中数学变式教学的调查分析及其应用

危 婕，廖小莲

(湖南人文科技学院 数学与金融学院，湖南 娄底 417000)



初中数学变式教学的调查分析及其应用

危 婕，廖小莲

(湖南人文科技学院 数学与金融学院，湖南 娄底 417000)

变式教学的运用由来已久，尤其是新课改下的变式教学，在我国现阶段初中数学教学过程中扮演着十分重要的角色，是每一位初中教师必须掌握的。但是在现实的初中数学教学过程中，不仅学生对变式教学的理解存在误区，而且较多教师也没有理解变式教学的本质，更是无法把握变式教学中的"度"。初中数学变式教学可应用一题多变，激励学生思维的变通性；一题多解，激活学生思维的发散性。

变式教学；初中数学教学；调查研究；变式应用

变式教学是当前中学教学中的一大热潮。变式是通过变更对象的非本质特征，变更观察事物的角度或方法，突出对象的本质特征，突出那些隐蔽的本质要素[1]。而变式教学则是在教师的指导下，把一个个的“问题”当作载体，因此变式教学是通过不同角度、不同侧面、不同情形、不同背景的变式手段使学生有效地加深认识和理解事物对象的本质特征的活动过程[2]。而数学变式教学是在数学对象本质不变的情况下，对数学非本质的特性进行多方面的适当的变形。初中数学变式教学是借助各种有效手段，将数学的定义、定理、题目等在各个方面、各个阶段、各个环境之间进行改变，有针对性地引导学生掌握并分析数学本质，使学生能够从数学知识和习题的表面分析其本质[3]。

一 初中数学变式教学的现状调查

(一)关于初中数学变式教学现状调查的提出

笔者在教育实习期间，发现现实数学教学中普遍存在的一个问题，就是学生在课堂上认真听讲，并积极完成了教师布置的作业，但是遇到题型变换的题目时，大都还是无从下手。教师在上课时讲的习题较多，但都是比较简单的，而且老师还喜欢在课后布置大量的习题，并且难度变化不大，就像是传统的题海战术，学生大部分的时间都花在了完成作业上面，但是考试效果却不怎么好。在教学的实际应用中，有些教师还没有认识到变式教学的本质，更没有在对课本了解透彻的基础上进行适当的变式，大都是带着教材进行笼统粗糙的变式，根本没有达到预计的教学效果。尤其在现今教育改革、全面推进新课改的大环境下，教师们更应该重新认识变式教学，在理解其实质的基础上，通过对教材的深刻理解，再精心进行变式加工，以此来实现对学生的引导。

(二)调查目的

调查主要是为了了解初中数学教师对变式教学的理解以及应用，还有初中学生看待数学的态度以及对变式教学的认知和接受能力。通过对调查数据的统计与分析，反映变式教学在初中数学教学中的现状，并结合教学实例，分析初中数学变式教学的原则以及应该注意的一些问题。

(三)调查对象

此次调查选择在洪江市芙蓉中学、怀化市铁路第一中学、黔阳三中进行，并在这3所中学里各选取了15名初中数学教师进行问卷调查，并有效地回收了45份调查问卷。在这45名教师中，教龄超过5年的有20人，教龄在5年及5年以内的有25人；学生的问卷调查，在洪江市芙蓉中学初中的3个年级各随机选取了20人，共发放了调查问卷60份，并且有效地回收了60份。在这60名学生中，有20名学生的数学成绩在中上，还有20名学生的数学成绩在中等，另外20名学生的数学基础比较差。

(四)调查方式

此次调查所用的工具是调查问卷，分别为教师调查问卷和学生调查问卷。教师调查问卷主要是关于教师对数学变式教学的理解与运用，共有15个问题；而学生调查问卷主要是关于学生对数学的认识及态度，还有学生对数学知识应用的体现以及对教师教学的掌握。

(五)调查结果与分析

1.教师问卷的调查结果与数据分析

通过对教师问卷数据的收集和整理，我们得到下面的结论：这3所中学的教师中有25人的教龄在5年及5年以下，用A5表示教龄在5年及以下的教师；还有20名教师的教龄在5年以上，用B5来表示教龄在5年以上的教师，因此对教师问卷进行数据统计时在5年教龄以上的教师与5年及以下教龄的教师之间进行对比分析。对变式教学的认知，在A5中，有60%的教师认为变式教学是一种教学模式，还有16%的教师说不清变式教学到底是什么；在B5中，有50%的教师认为变式教学是一种教学手段，35%的教师认为变式教学是一种教学模式。无论是A5教师还是B5教师，都没有人认为变式教学是一种教学现象，也没有人对变式教学有多种认知，都是单一地认为变式教学是一种教学模式、教学手段、教学思想，甚至有些教师自己都不知道变式教学到底是什么，从这一点上，我们可以清楚地感受到教师对变式教学认知的盲目。在A5教师中，有44%的教师在自己上中学时偶尔从他们老师那里接触到变式教学，大都是很少接受过甚至没有接受过变式教学；在B5教师中，有15%的教师在自己上中学时经常能从他们老师那里接触到变式教学，也还有55%的教师偶尔才能接触到变式教学，但是从A5教师与B5教师的对比中，我们可以发现变式教学在某一段时期没有被重视。在对变式教学是否能够实现有效教学的问题上，A5教师中有48%的人认为变式教学必不可少，还有36%的教师认为变式教学有部分用途；B5教师中有65%的人认为变式教学必不可少，还有35%的教师认为变式教学有部分用途。从这2组数据看来，无论是A5教师还是B5教师，在他们看来变式教学都是占有重要地位的。

A5教师中有52%的教师偶尔才会将变式教学使用到数学教学中去，只有32%的教师会经常运用变式教学，甚至有12%的教师没有将变式教学融入到自己的数学教学中；B5教师中有60%的教师会经常运用变式教学，还有35%的教师偶尔也会将变式教学运用到数学教学中来。由此可以看出教龄不一样的教师在对变式教学的运用上也有很大的差别，教龄长的B5教师更加注重变式教学在数学教学中的运用。在问及如何使用到变式教学时，A5教师中有32%的教师是课前有意识、有设计的，还有28%的教师是受某些教学问题的启发，由上课得到的灵感、没有刻意设计变式教学的教师在A5教师中占24%；而在B5教师中，有60%的教师是课前有意识地去设计变式教学。由此可以看出教龄更长的B5教师更加注重对变式教学的设计。

在具体教学环节中设计变式教学时，A5教师中选择在创设情境、探究新课中设置变式教学的最多，分别高达88%和68%；B5教师中选择环节最多的也是创设情境和探究新课，分别高达100%和80%。由此可见在设置变式教学时，教师们都喜欢在新课导入中进行变式，从而引导学生进行新课探索，在教学环节变式教学设置的选择上，教师们选择了多个选项，可见变式教学能运用到多个教学环节中去，应该引起广泛重视。对于数学课堂教学中变式的体现，A5教师中选择一题多解和一题多变的最多，分别为64%和40%；而在B5教师中有高达85%的教师选择了一题多变，还有60%的教师选择了一题多解。由此我们可以看出教龄长的教师更加注重一题多变，着重关注问题的变式，大多数教师认为变式教学的主要形式就是变式练习，由此可见大多数教师都很注重多形式的变式教学。

在数学课堂教学上，关于是否引导学生挖掘或引申某一内容中，A5教师里有高达52%的教师表示经常引导学生，有32%的教师表示很少去引导学生挖掘其他内容；而B5教师中有高达75%的教师表示经常引导学生这样做，10%的教师很少会去引导学生。由此我们看出教龄长的B5教师更加注重对学生的引导， 会从学生实际出发，以学生为本，对学生加以引导。在对最关心的课堂教学顺序中，A5教师中分别有40%和48%的教师表示最关心学生的理解顺序和知识的逻辑顺序；而在B5教师中，有40%的教师最关心的是学生理解的顺序，60%的教师更加倾向于关心知识的逻辑顺序。教龄长的教师更加倾向于对基础知识的理解。在对某一知识点中同水平的数学问题反复操练的看法中，A5教师里有56%的教师认为这样做既有助于记忆又能促进理解，还有8%的教师认为只要懂了就不要再反复操练；而B5教师里有45%的教师认同这样做既有助于记忆又能促进理解，还有高达30%的教师认为只要懂了就不要再反复操练，在这一点上教龄不同的教师认知差异较大，教龄短的教师认为熟能生巧，希望能有大量时间进行反复操练。由此可以看出，教龄长的教师更加注重教法，而教龄短的教师则更多希望通过多多练习来熟练。在教材中出现操作性内容时，A5教师里有52%的教师会考虑课容量，如果课容量太大，便不会进行操作，仅仅只有16%的教师会设计操作性内容并结合实际尽量优化；而B5教师里有高达35%的教师会设计操作性内容并结合实际尽量优化。由此可以看出教龄长的教师更有耐心，在变式教学中会花费更多时间去设计教学。

针对教师在变式教学中设计题量和难度的调查问题中，无论是教龄短还是教龄长的教师，都选择会在变式教学中给出大量变式题，在设置变式难度时，近乎一半的教师都选择设置很多常见的简单变式题型，只有极少数的教师选择设置适量的题型，并将难度把握好。只不过教龄长的教师在设置变式教学的题目时，会有更多实际教学经验，显而易见，较多教师对变式教学的量和度仍然把握不好，还需要对变式教学的理论进一步深究，并在自己的教学实践中不断积累经验。

2.学生问卷的调查结果与数据分析

此次调查分别在初一年级、初二年级以及初三年级中抽选了20名学生，对学生问卷调查数据的收集和整理结果：其中有50%的学生对学习数学还是比较感兴趣的，但是在学习数学过程中58.33%的学生偶尔才能有成功的体验，说明尽管有许多学生对数学比较感兴趣，但是在面对数学难点时，很少学生能够感受到学习数学的成功。所以才会有越来越多的学生觉得数学很难，即使花费很多时间也得不到预计的成功，这种畏难心理一旦开始，便会一发不可收拾，学生便对数学开始有抵触心理。在谈到对学习数学的目的时，50%的学生表示是为了升学考试，还有25%的学生表示自己也不清楚，老师教什么他们就跟着学什么，这些都说明在分数的大压力下，学生不得不在题海中与数学作斗争。在学生平常的练习过程中，有41.67%的学生觉得能用一种方法做出来就足够，还有33.33%的学生会在做不出来时放弃，这进一步体现了学生的畏难心理，在遇到难题时没有钻研思考，造成现在较多学生习惯性地抄袭作业，部分学生将作业当成任务，做完之后不会再去思考探索。这些都是当前教育环境下，初中数学变式教学暴露的比较常见的弊端。

调查的学生中有50%的学生对变式教学完全不了解，仅有16.67%的学生对变式教学十分了解，一方面是对学生认知水平的暴露，另一方面显露出教师对学生教育的不足，可见变式教学的开展还存在很多问题。教师既没有将变式教学的理论认知教给学生，也没有将变式教学很好地融入到数学教学中来，正所谓“知其然，不知其所以然”，这使学生在变式教学的理解上存在很大的误区。在平常的解题过程中，有66.66%的学生只是有时能够发现数学变式的存在，这进一步说明学生对变式教学的认知存在很大的不足，暴露了变式教学在数学教学中存在的不足。另外有43.33%的学生表示在上数学复习课时，老师针对学生出错的问题进行相关变式训练的补充，这对他们今后在数学学习上很有帮助，正确运用变式教学能够让学生更加轻松有效地学习数学。还有71.67%的学生觉得数学老师布置的作业太多，因为有部分老师认为只有大量地做题才能提高数学成绩，但是这样很容易陷入题海战术。如果我们做一道题就理解一类题，在原题上进行变式，一点点地加大难度、改变条件和提问，这样就更容易理解数学知识的本质，由此说明变式教学在初中数学教学中是十分重要且必要的。

在老师出题后，有58.33%的学生赞同先审题，想一想，再由自己和其他同学将所能想到的知识、思路、方法都列举出来，想不到的再由大家补充、完善，然后由师生实施各种想法，最后由老师点评、讲解。这说明学生还是希望能先进行自主思考，与同学一起讨论，这一点也特别符合新课改的要求，在大家各抒己见之后由老师来点评这些方法。变式教学中的一题多解就显得格外突出，虽然这个讨论深究的过程加大了课堂容量，但是一题多解就是为了找出更加简便有效的解题方法，从而实现多题一解。有50%的学生表示比较喜欢老师在上课时经常运用变式训练，一方面将实际生活融入到数学教学中来，激发了学生探索数学知识的兴趣；另一方面合理设置不同难度的变式题组，让学生善于思考，勇于探索，不断挖掘数学知识的新大陆，同时能很好地培养学生的数学思维和归纳能力。

在对角平分线性质的表达方式上，有66.68%的学生习惯于直接用两个角相等来表述角平分线的性质，这对学生来说是一种思维定式，总是习惯于某一种自己常用的理论。在对8a+9的判定中，只有6.67%的学生认为它既是运算结果，又是运算过程，41.66%的学生认为它是一种运算过程，33.33%的学生认为它是一种运算结果，这种单一式的认知相当普遍，也可以看出学生数学思维的束缚。在对如何判定一个三角形是否为直角三角形时，有50%的学生习惯于运用勾股定理来判定，只有8.33%的学生会运用三角形一边上的中线等于这条边的一半来判定。这些都能够看出学生的习惯对解题的影响，并且学生的认知水平很大程度上决定了解题的能力。如此一来，变式教学显得尤为重要，让学生不再囚禁在自己的思维定式里，挖掘自身无限的可能。

(六)调查结论

由上面的调查数据和结果分析可以看出，无论是教师还是学生，对变式教学的本质认知和理解仍存在较大不足，因而教师在将变式教学运用到初中数学教学时，由于自身认知的不足，在设计变式教学时有诸多误区，更容易让学生对此产生误解，甚至摸不清头脑，不明白变式教学究竟为何物。虽然现在变式教学运用广泛且频繁，但是很多教师没有抓住教学目标以及教学的重难点，只是空泛地进行表面的变式。还有就是变式量太多，让学生再次陷入题海战术。有些教师没能把握好变式教学的难度，太简单、太复杂的变式训练都达不到预期的教学效果。所以我们还是得先回归到理论的高度上来，从理论上研究透彻到底什么是变式教学，将变式教学应用到初中数学教学中又需要遵循什么样的原则，以及在实际教学案例中的常用变式教学方法和手段。

二 结合教学案例探讨变式教学在初中数学教学中的应用

(一)一题多变，激励学生思维的变通性

“一题多变”是通过题目的引申、变化、发散，提供问题的背景，揭示问题间的逻辑关系。在课堂上进行“一题多变”的适当运用，不仅可以加深学生对所学知识的理解，而且能激发学生的探究精神和学习热情，更能达到拓展数学思维的作用[4]。“一题多变”教学模式变通能力极强，摆脱了传统教学的羁绊，改变了学生的固定思维[5]。

案例1 A、B两地相距1000公里，一列慢车从A地开出，速度为80公里/小时，一特快车从B地开出，速度为120公里/小时。

问题1 快车与慢车同时相向出发，多久两列车能够相遇？

问题2 慢车先出发5小时，随后快车再出发，两列车相向驶出，请问在快车开出多长时间后两列车能够相遇？

问题3 快车跟慢车同时同向出发，此时慢车在快车前面100公里处，请问多长时间快车能够追上慢车？

问题4 慢车先开出1小时，随后两列车再同向开出，慢车在快车的前面，请问在快车驶出后几小时能够追赶上慢车？

案例1分别给出了“两地的距离、慢车的速度和快车的速度”这3个条件，设置了相同的条件，然后在问题上进行改变，还在一些问题中加设了新的条件，虽然有不一样的地方，但是这组变式题的本质都是应用题中的行程问题，均需运用“速度×时间=路程”这个等量关系。在初一学生刚开始学习用一元一次方程解决行程问题的应用题时，相遇问题和追及问题一直是较难突破的重难点，学生对题目的理解还有待加强，尤其是分别遇到多个问题时很容易混淆。

问题1是最基础的运用一元一次方程解行程应用题中的相遇问题，由于两列车同时相向行驶，那么从它们开始出发直到相遇所用的时间是相同的，并且两列车行驶的路程加起来就是两地的距离，可列出等量关系：(慢车速度+快车速度)×两车相遇的时间=两地间的距离。

问题2是在问题1的基础上进行变式，改变一个条件，由原先的两列车同时出发变为慢车先出发，要求的仍然是两列车相遇所用的时间，但有一辆车先出发，所以有等量关系：慢车速度×慢车先出发的时间+(慢车速度+快车速度)×两列车相遇所用时间=两地距离。

问题3是两列车同时同向出发，此时慢车在快车的前面，那么两列车是同时向慢车所在的方向出发的，这里就存在一个追及问题，快车在后面追赶慢车，题目要求的便是快车追上慢车所用的时间，两车所用的时间是一样的，便可以列出等量关系：快车速度×快车追上慢车所用时间=慢车速度×快车追上慢车所用时间+两地距离。

问题4则是在问题3的基础上，由同时出发变式为慢车先出发，题目所求仍为快车追上慢车所用的时间，那么我们在利用路程等量关系列等式时应该注意要在慢车行驶的路程上加上慢车先行驶的路程，则可以列出等量关系：快车速度×在慢车先出发后快车再出发追赶上慢车所用的时间=两地距离+慢车速度×慢车先出发的时间+慢车速度×在慢车先出发后快车再出发追赶上慢车所用的时间。

在案例1这一组变式题组中，将用一元一次方程解行程问题中的相遇和追及问题很形象地表述出来，另外在这个基础上加入同时或不同时出发的干扰条件，让学生在理解原题的基础上，进行进一步的探索。但是有一点没有变，这组题的本质都是运用“速度×时间=路程”来列出每个问题中的等量关系式，最后求出未知数从而得出答案。另外在解决这类行程问题时，教师要引导学生学会画简易的表述题意的路程图，将渗透了数形结合的数学思想渗入课堂教学中。一题多变的变式教学方法，可以通过联想、归纳等方式培养学生思维的变通性。

(二)一题多解，激活学生思维的发散性

一题多解就是从不同的角度、不同的侧面分析同一问题中的已知条件以及题目中所隐含的条件，运用所学知识使条件和结论之间建构为某一数学模型，用不同的解法得到相同结果的思维活动过程[6]。

案例2 某工厂7月生产电视250台，8月生产300台，请问8月比7月增产了百分之几？

这是一道实际生产的应用题，题目要求的是8月比7月增产了多少百分比。这里我们可以有两种思路去分析：一方面可以先求出8月比7月增产的台数，然后再计算8月比7月增产的百分数，即：

另一方面可以先计算8月产量是7月产量的百分之多少，再计算8月比7月增产的百分数，即：

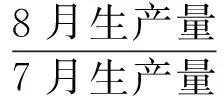
解法1 先求出8月比7月增产的台数，再计算8月比7月增产的百分数，即：

(300-250)÷250=20%.

解法2 先计算8月是7月的百分之几，再计算8月比7月增产的百分数，即：

300÷250-1=1.2-1=20%.

一题多解，一方面是为了拓宽学生的思维视野，另一方面也可以规避题海战术带来的重复和盲目。教师在学生用各自的思考方式得出不同解法后，再一起进行归纳总结，得出最简便的解题方法。学生在以后遇到相同题型时，能够从大脑中迅速搜索出最简便有效的方法。运用一题多解的变式教学方法，可通过多角度思考来培养学生思维的发散性。

[1]孙孜.变式教学应注意的几个问题[J].教育实践与研究：中学版，2009(6)：37-39.

[2]荣平.变式教学初探[J].考试周刊，2015(92)：44-44.

[3]蔡维.初中数学变式教学研究[J].新课程导学，2014(14)：79-79.

[4]向星.变式教学在初中数学中的应用研究[D].长沙：湖南师范大学教育科学学院，2008..

[5]邓朵朵.变式教学在高中数学教学中的应用探究[D].西安：陕西师范大学研究生院，2014.

[6]谢传文.数学教师对变式教学有效性的认识研究[D].曲阜：曲阜师范大学数学科学学院，2013.

(责任编校：杨丽英)

An Analysis of Pedagogy of Variation in Junior Mathematics Teaching and Its Application

WEIJie,LIAOXiao-lia

(School of Mathematics and Finance, Hunan University of Humanities, Science and Technology, Loudi 417000, China)

Pedagogy of variation has long been adopted in classroom teaching.Under the background of curriculum reform, it is now playing a very important role in junior math teaching in China, and every junior high school teacher is supposed to master it.But in reality, not only students have misunderstandings of the pedagogy, many teachers also fail to understand its essence, thus failing to grasp the difficult points and key points in teaching.Math teachers therefore are suggested to employ the method by presenting one problem with many forms to cultivate students′ flexible thinking, and providing multiple solutions to one problem to cultivate their divergent thinking.

pedagogy of variation; junior high mathematics teaching; investigations; application of variation

2016-05-20.

危婕(1994—)，女，湖南怀化人，湖南人文科技学院数学与金融学院2016届本科毕业生；

廖小莲(1970—)，女，湖南新化人，湖南人文科技学院数学与金融学院副教授，本文指导老师，研究方向：基础数学。

O12

A

1673-0712(2016)05-0109-06