多导体传输线的邻近效应和分布参数研究

逯贵祯 郭庆新 曾冬冬

(中国传媒大学信息工程学院,北京100024)



多导体传输线的邻近效应和分布参数研究

逯贵祯 郭庆新 曾冬冬

(中国传媒大学信息工程学院,北京100024)

随着多导体传输线内各导体之间间距的减小,导体之间的近邻效应对传输线的分布参数和传输特性的影响越来越大．为此,我们针对三种典型的传输线结构,分别建立了基于矢势有限元方法分析的多导体传输线的模型,并分析了近邻效应对磁通密度和分布电感的影响．利用提出的方法计算了同轴传输线的单位长度分布电感,并将它与采用解析方法得到的结果进行比较来证明该方法的正确性．计算双线传输线在不同间距时的单位长度电感,与理论分析得到的结果相比较验证了导线间距越小,近邻效应对单位长度电感的影响越大．最后,计算考虑了近邻效应的耦合微带线的电感矩阵,并将它与其他不考虑近邻效应的方法得到的结果相比较,说明近邻效应对传输线电感矩阵的影响．

多导体传输线;近邻效应;电感矩阵;矢势有限元

DOI 10.13443/j.cjors.2015072201

引 言

高速数字电路和集成电路的发展,要求信号互联线之间的间隔不断减小,因此多导体传输线的横向尺寸也在不断减小,由此带来信号线之间的干扰在不断增大．目前研究人员也从不同的角度,例如瞬态分析[1-2]、分布参数等方面,对多导体传输线之间的互扰问题进行研究．实际上多导体传输线之间的互扰问题与传输线之间的电容矩阵、电感矩阵存在密切的联系[3]．研究分析多导体传输线之间的电容矩阵和电感矩阵对于设计和优化高速数据信号的传输具有重要的工程应用意义．为了更加准确地分析和设计信号互联线,精确的多导体传输线电容矩阵和电感矩阵的计算是非常重要的．

多导体传输线电容矩阵和电感矩阵的计算可以采用解析方法也可以采用数值方法进行计算．解析计算方法通常要求传输线的结构具有一定的规则形状,比如柱形或圆柱形界面,且导体周围的介质是均匀的．而数值计算方法没有这个要求,可以适用各种复杂的结构,所以它的适用性很强．在众多的数值计算方法中,有限元方法非常适用于各种横截面的传输线结构和不均匀的复杂介质．研究人员已经利用有限元方法对各种传输线进行研究．如Musa采用有限元方法计算了多导体传输线的电容矩阵和电感矩阵[4]．他的方法首先采用静电场的泊松方程计算多导体传输线的电容矩阵C,然后根据关系式:L=μ0ε0C-1,求出电感矩阵L．这种方法的一个不足之处是不能研究相邻导体的近邻效应．为了研究多导体传输线之间的近邻效应,需要研究导体中电流分布对互感矩阵的影响．基于矢势的有限元方法研究多导体传输线最早应用于电力传输系统．电力系统研究传输线的电流分布主要是研究趋肤效应对传输效率的影响以及场分布对环境的影响．如M.V.K. Chari和Z.J. Csendes[5]采用基于矢势的有限元方法研究了多导体传输线中涡旋电流对导体电流密度分布的影响,特别是趋肤效应的影响．从物理原理看,导电介质中的涡旋电流会影响磁感应强度,进而影响电流密度分布．在该分析过程中,他假定矢势A只有传播方向的分量,而且在传播方向的电流分量中忽略了位移电流的影响．在这个假定下,电场与磁场的相互影响被忽略,与标势函数相联系的电流作为驱动电流源,与矢势A相联系的涡旋电流是矢势A的函数,所得到的微分方程是关于矢势A的扩散方程．该方法针对开放空间和磁性材料边界问题求解了导体中趋肤电流分布问题．J. Weiss[6]改进了上述求解方法,提出了把与电势和电导率有关的电流以及涡旋电流都作为未知量,这样可以一步求解得到导体中的电流分布,并用此方法分析了电力系统三相交流电问题．Hong-Kyu Kim[7]采用三维矢势有限元方法研究了导线的趋肤效应．为了减少未知量数目,对每个导体与标势函数相联系未知变量的源电流用一个等效的比例常数代替,从而减少了未知量数目,而未知常数通过迭代的方法确定．不过该方法需要对迭代参数进行合理的选择,才可能达到收敛的结果．S. Cristina[8]用矢量有限元方法计算了电力传输线的分布参数．K.J. Satsios[9]用基于矢势有限元方法研究非均匀地球表面功率传输线的涡旋电流和磁场分布,分析非均匀地面介质对导线涡旋电流和磁场分布的影响．

在以下研究中,采用基于矢势的有限元方法分析了多导体传输线的分布参数矩阵和磁通密度分布．为了使用基于矢势的有限元方法,首先需要根据传输线的结构来确定传输线的分析模型和矢势的边界条件．我们利用矢势有限元分别研究了封闭结构和开放结构的单位长度电感,给出了相应边界条件的要求,并对数值计算结果与解析方法结果进行了比较,证明数值计算模型的有效性和近邻效应的影响．为了进一步研究近邻效应对传输线电感矩阵的影响,文章分析了双微带线结构．得到的计算结果与文献[4]采用电容矩阵计算的电感矩阵进行了比较．和以前的方法不同的是,在计算电感矩阵时,我们提出的方法没有利用电感、电容和光速之间的关系,而是采用静态电场与静态磁场的方法直接独立提取传输线的电感和电容．

1 理论分析

如果多导体传输线内各个导体均是理想导体,则电磁波沿着导线传播横电磁波．对于非理想导体,导线金属具有有限电导率,因而在传播方向有一定大小的纵向电场分量,该纵向电场分量引起纵向电流．纵向电流可以分为三个部分,一是由电压差引起的传导电流,二是位移电流分量,另一个部分是涡旋电流部分．位移电流和涡旋电流与工作频率有关,影响电流的趋肤深度,进而引起传输功率的损失．为了分析传输线的分布参数,在进行准横电磁波近似时,如果忽略位移电流,麦克斯韦方程组可以写成:

×B=μJ;

(1)

×E=-jωB;

(2)

·B=0;

(3)

·E=0.

(4)

引入矢势A,电场和磁场可以分别表示为:

(5)

(6)

式中φ是标势函数,与静电场有关．忽略位移电流后的电流密度为:

J=Js+Je=-σφ-jωσA.

(7)

式中: σ是导体中的电导率; Je是涡旋电流; Js是导线中外加电压引起的传导电流．在以下研究中,分析多导体传输线的分布电感参数的近邻效应时,忽略了涡旋电流．矢势A的偏微分方程为:

××A=μJ.

(8)

公式(8)对应的有限元泛函公式为:

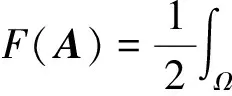
μ∫ΩJ·AdΩ+∫Sn×(×A)·dS.

(9)

对式(9)取变分δF=0可以得到矢势有限元的计算公式．矢势A的第一类边界条件由式(10)确定．

n×A=P.

(10)

式中P是边界上确定的矢势值．

2 多导体传输线的数值计算

多导体传输线中,单位长度电感矩阵L的元素与穿过传输线第k个电路单位长度的总磁通和所有产生该磁通的传输线上的电流关系为:

ψ=L·I.

(11)

用矩阵形式,公式(11)可以表示为:

(12)

在采用基于矢势的有限元方法计算自感矩阵过程中,首先利用有限元方法,求出每个导线施加外部电流后产生的磁场,然后利用电感矩阵的定义公式(12)计算多导体传输线的电感矩阵．为了进行有限元分析,需要给出物理量的边界条件．矢势是计算电磁场问题的一个辅助函数,因此要根据研究问题,将电磁场边界条件转化为矢势的边界条件．以下的分析计算分别针对封闭结构、开放结构和耦合结构的传输线进行研究．

2.1 同轴传输线

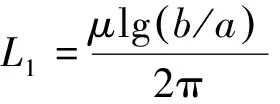
图1 同轴线横截面磁通密度分布

从图1可以看到,磁通密度沿径向是非均匀分布的,特别是在内导体的内部,磁通量是从最小值逐渐增加,在内导体边界附近达到最大值,然后又开始降低．可以预见,随着内导体截面积增加,对同轴线的电感数值的影响也会增加．同轴线的电感数值是通过内外导体之间连线的积分得到的．

图2给出了外导体半径从2.3 mm到3.2 mm变化对同轴线电感的影响．图中分别画出了通过解析法计算得到的电感值与通过此数值方法计算得到的电感值．从图2曲线可以看到,随着外导体半径增加,同轴线的电感在增加．通过解析表达式理论计算得到的电感值与通过此数值方法计算得到的电感值的一致性很好,证明了利用该方法计算电感是有效的．

图2 同轴线外半径不同时的单位长度电感

2.2 平行双线传输线

平行双线传输线是一种典型开放结构的传输线,其电磁能量主要集中在平行双线附近,但是可以延伸到无限大空间．利用有限元对其进行分析时需要对计算空间进行截断,为此我们采用无限元方法作空间截断．这里研究的平行双线的线间距为3 mm,导线半径从0.1 mm到1 mm之间变化．进行有限元分析时,对其中的一个导线施加正向均匀电流密度,另一个导线施加反向均匀电流密度．

磁通的计算是通过两个导体外边界之间的连线进行积分得到的．图3是基于矢势有限元法得到的平行双线的磁通密度分布．

图3 平行双线的横截面磁通密度分布

从图3可以看到,平行双线的横截面磁通密度分布在导线中也不是均匀分布的,在两个导线近端,磁通密度变大;同时,大部分磁通密度集中在双导线附近．

图4给出了传输线导体半径从0.1 mm到1 mm变化对平行双线电感的影响,同样,图中同时画出了通过解析法计算得到的电感值与通过我们提出的数值方法计算得到的电感值,解析法采用的表达式为L2=μarcosh(D/2a)/π,其中D是两根导线之间的间距,a是单根导线的半径[10]．从图4曲线可以看到,两种方法得到的结果有稍微的偏差,但趋势一致,即随着导体半径增加,传输线的电感在减少．同时解析计算的电感值与数值计算的电感值的差值也在增加．产生差值的主要原因是解析公式中假定导体的磁通是均匀分布的．由此说明,当传输线之间距离减少时,近邻效应是必须考虑的一个重要因素．

2.3 耦合微带线

由于存在互感和互电容,两条并行排列的微带线之间会产生串扰．图5给出了一个耦合微带线结构．该微带线结构与文献[4]中的尺寸结构一致,即每个微带线宽度w=500μm,厚度t=17μm,微带线的间隔s=500μm,微带线基板厚度h=635μm,相对介电常数εr=10.8．文献[4]采用有限元静电场公式,首先计算耦合微带线的电容矩阵,然后由电容矩阵和传播速度得到电感矩阵．但是,在该方法中,没有考虑传输线近邻效应的影响．我们采用基于矢势的有限元方法直接计算传输线的电感矩阵,其优点是可以考虑导线近邻效应的影响．图6给出了采用此方法计算得到的耦合微带线的磁通密度分布．从图6可以看到,两个微带线的近邻效应对磁通密度分布产生影响．

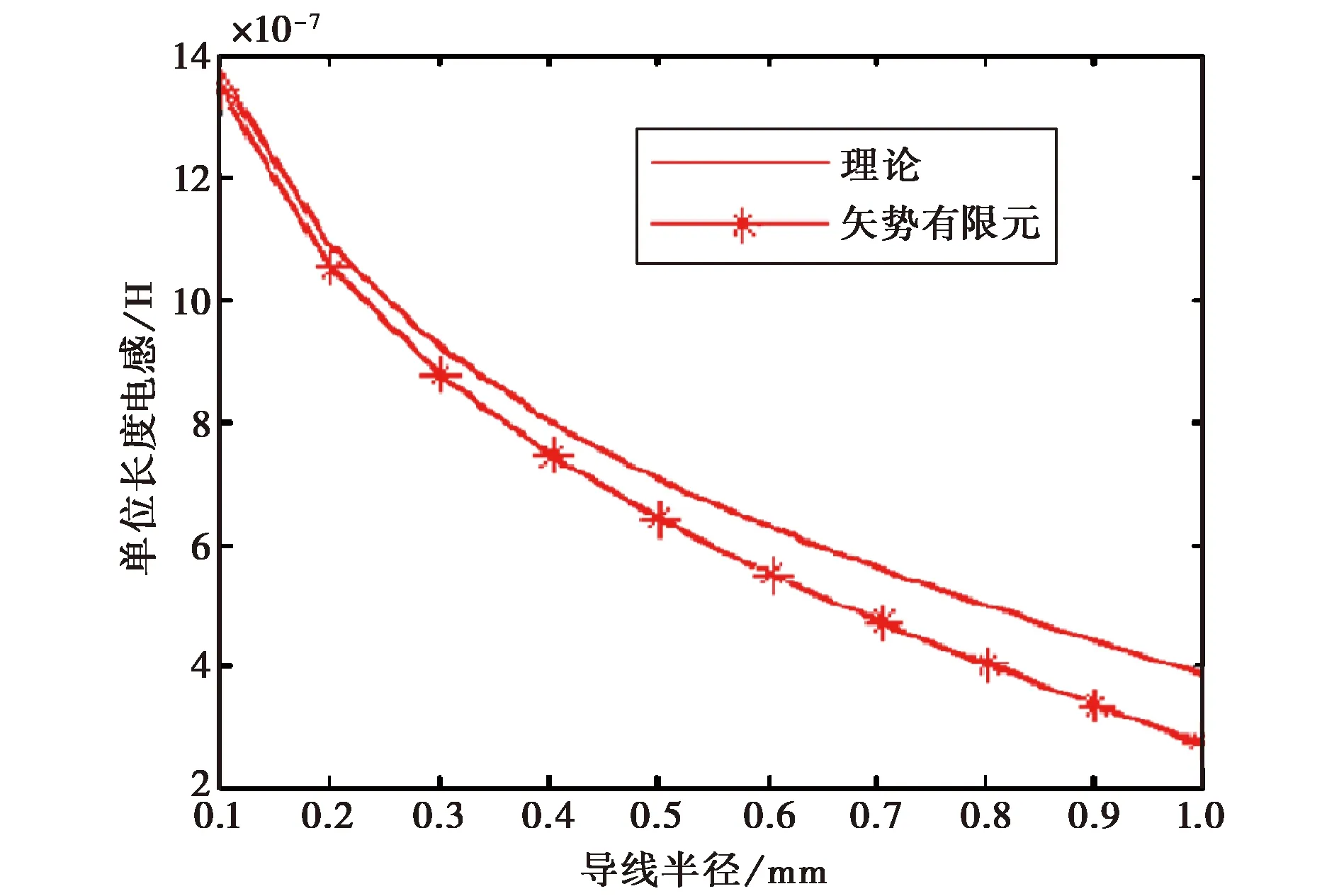
图4 平行双线的电感(两根导线距离3 mm,每根导线半径从0.1 mm变化到1 mm．)

图5 平行耦合微带线的几何结构

图6 耦合微带线的磁通密度分布

根据多导体传输线电感矩阵的定义,耦合微带线的电感矩阵中的自感可以通过计算微带线中心到接地面的磁通和导线的电流得到;而两个微带传输线之间的互感通过计算两条微带线之间边缘连线的磁通得到．由于问题具有对称性,另一条微带线的自感和互感可以同时得到．采用这个方法计算得到的电感矩阵与文献[4]得到的电感矩阵结果列于表1．

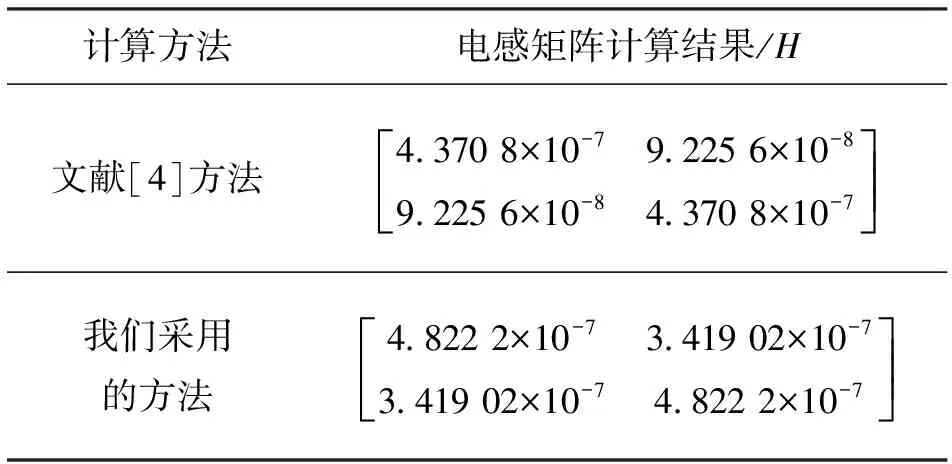
表1 耦合微带线电感矩阵

从表1可以看到,按照我们提出的方法计算得到的电感矩阵要大于文献[4]方法计算的电感矩阵,其主要原因是因为传输线近邻效应使两条微带线之间的磁通密度增加,因此互感会大大增加．互感的增加会进一步增加耦合微带线之间的串扰．

3 结 论

与采用基于静电场标势的有限元方法相比,基于矢势有限元方法可以考虑传输线之间的近邻效应．因此,我们采用基于矢势有限元方法计算多导体传输线的电感参数和磁通分布,研究近邻效应的影响．

我们分别分析计算了三种典型的传输线结构．第一种传输线结构是封闭结构的同轴传输线．在同轴传输线的有限元计算中,外导体边界采用切向矢势为零的边界条件,它等效于理想导体边界条件．计算的传输线单位长度电感与解析表达式得到的电感进行了比较,两种计算结果一致性很好,证明了利用这种方法的可行性．第二种是一种典型的开放式结构——平行双线传输线．由于其磁场延伸到无穷大区域,为了进行有限元计算,我们对这个开放的传输线结构采用无限元单元截断．计算结果显示在双线距离较大的时候与解析结果比较接近．为了研究近邻效应,我们固定双导线之间的中心距离,然后改变传输线导体半径来改变双导线表面间的距离进行分别计算,从而得到了传输线电感与导线半径的关系曲线．通过与平行双线的解析公式得到的结果比较可以看出,随着导线半径的增加,有限元计算和解析公式计算结果的差值在增加,这个差值反映了近邻效应的影响．第三种是一个耦合的微带线结构．采用基于矢势有限元方法计算电感矩阵并与其它文献中没有考虑近邻效应所得到的结果进行比较．比较结果显示,传输线的电感矩阵有较大的差别,这个差别同样反映了传输线近邻效应对电感矩阵的影响．

[1] 张玉廷, 蔡智, 张华. 多导体传输线瞬态响应研究[J]. 电波科学学报, 2014, 29(1): 377-384.

ZHANGYT,CAIZ,ZHANGH.Transientanalysisofmulticonductortransmissionlines[J].Chinesejournalofradioscience, 2014, 29(1): 377-384. (inChinese)

[2] 李莉, 冀维林. 端接非线性负载的不等长传输线瞬态分析[J]. 电波科学学报, 2009, 24(3): 529-532.

LIL,JIWL.Transientanalysisofunequallengthmulticonductortransmissionlinesloadedbynonlineardevices[J].Chinesejournalofradioscience, 2009, 24(3): 529-532. (inChinese)

[3] 李莉, 万里兮, 咸金龙, 等. 多导体传输线互耦试验研究[J]. 电波科学学报, 1999, 14(2):166-171.

LIL,WANLX,XIANJL,etal.Experimentofmutualcouplingofmuticonductortransmissionlines[J].Chinesejournalofradioscience, 1999, 14(2): 166-171. (inChinese)

[4]MUSASM,SADIKUMNO.Calculatingthecapacitanceandinductanceofmulticonductortransmissionlines[J].Thetechnologyinterfaceinternationaljournal, 2008(2): 300-304.

[5]CHARIMVK,CSENDESZJ.Finiteelementanalysisoftheskineffectincurrentcarryingconductors[J].IEEEtransactionsonmagnetics, 1977, 13(5): 1125-1127.

[6]WEISSJ.AOne-stepfiniteelementmethodFormulticonductorskineffectproblems[J].IEEEtransactionsonpowerapparatusandsystems, 1982, 101(10): 3796-3800.

[7]KIMHK,JUNGJK,PARKKY,etal.Efficienttechniquefor3-Dfiniteelementanalysisofskineffectincurrent-carryingconductors[J].IEEEtransactionsonmagnetics, 2004, 40(2): 1326-1329.

[8]CRISTINAS,FELIZIANIM.Afiniteelementtechniqueformulticonductorcableparameterscalculation[J].IEEEtransactionsonmagnetics, 1985, 25(4): 2986-2988.

[9]LABRIDISDP,DOKOPOULOSPS.Finiteelementcomputationoffieldandeddycurrentsofastemconsistingofapowertransmissionlineaboveconductorsburiedinnonhomogeneousearth[J].IEEEtransactionsonpowerdelivery, 1998, 13(3): 876-882.

[10]POZARDM. 微波工程[M]. 张肇仪, 周乐柱, 吴德明, 等, 译. 3版. 北京: 电子工业出版社, 2010: 47.作者简介

逯贵祯 (1957-),男,北京人，中国传媒大学教授,博士生导师,主要研究方向电波传播、电磁散射与逆散射、计算电磁学、天线技术、射频与微波电路、电磁兼容等．

郭庆新 (1974-)，男,中国传媒大学副教授,主要研究方向为天线技术、射频与微波无源器件、射频与微波电路等．

Proximity effect and the distribution parameters of multi-conductor transmission line

LU Guizhen GUO Qingxin ZENG Dongdong

(Information Engineering school, Communication University of China, Beijing 100024, China)

The effects of the proximity effect and the distribution parameters on the reflection and transmission parameters of a multi-conductor transmission line increase significantly when the gap between two adjacent conductors decreases. Considering the proximity effect, we calculate the distribution inductance and the magnetic flux density of three typical multi-conductor transmission lines by applying the vector potential finite element method. The first case is a coax with a closed structure. The proposed numerical results agree well with the analytical results, which verify that the proposed method is effective. The second one is a parallel line with an opened structure, of which the infinite calculation domain has been truncated by the infinite element method during calculation. The comparison implies that the proximity effect influences the per-unit-length inductance of multi-conductor lines. The last instance is a coupled microstrip. The distribution of the magnetic flux density around the coupled lines show that it is affected by the proximity effect. The inductance matrix obtained differs from that of the previous work, in which the proximity effect has not been taken into account. All 3 cases imply that the vector potential finite element method is suitable for calculating the distribution parameters of multi-conductor transmission line with the proximity effect.

multi-conductor transmission line; proximity effect; inductance matrix; the vector potential finite element method

10.13443/j.cjors.2015072201

2015-07-22

TM154

A

1005-0388(2016)03-0611-06

逯贵祯, 郭庆新, 曾冬冬. 多导体传输线的邻近效应和分布参数研究[J]. 电波科学学报,2016,31(3):611-615+622.

LU G Z, GUO Q X, ZENG D D. Proximity effect and the distribution parameters of multi-conductor transmission line [J]. Chinese journal of radio science,2016,31(3):611-615+622. (in Chinese). DOI: 10.13443/j.cjors.2015072201

联系人： 逯贵祯 E-mail： luguizhen@cuc.edu.cn