降雨入渗对坡积土边坡渗流特征及稳定性的影响
2016-11-29康津军
康津军
(湖南省新化公路桥梁建设工程有限公司,湖南娄底 417600)
降雨入渗对坡积土边坡渗流特征及稳定性的影响
康津军
(湖南省新化公路桥梁建设工程有限公司,湖南娄底 417600)
基于非饱和渗流及抗剪强度理论,采用有限元数值模拟方法对降雨条件下边坡渗流特征及安全系数变化规律进行计算。结果表明,降雨开始后,降雨入渗影响区内土体的孔隙水压力、体积含水率逐渐升高,暂态饱和区自坡面往内逐渐扩展,边坡安全系数不断降低;降雨停止后,坡面附近土体的孔隙水压力、体积含水率持续降低,暂态饱和区自坡顶往坡脚附近迅速消散,边坡安全系数缓慢升高;降雨期间,坡面附近土体的孔隙水压力、体积含水率、暂态饱和区面积、边坡安全系数均与降雨强度成正比。
公路;坡积土;孔隙水压力;体积含水率;暂态饱和区;安全系数
降雨是引起边坡失稳的主要外部因素之一,雨水渗入边坡后,一方面,坡面附近土体的基质吸力逐渐丧失,边坡的抗滑力持续降低,坡体的安全储备减小;另一方面,降雨入渗影响区内土体的饱和度持续增大,重度也增大,边坡的下滑力不断增大,坡体的安全储备进一步减小。对于坡积土边坡,由于坡积土土颗粒之间较为松散,土体的孔隙较大,渗透性较好,其稳定性受降雨入渗的影响更为显著。由于降雨入渗是引起坡积土边坡失稳的关键因素,对降雨条件下坡积土边坡渗流特征及稳定性变化规律的研究显得十分紧迫。
目前已有的针对降雨条件下边坡渗流特征的研究大多只分析了降雨过程中边坡孔隙水压力、饱和度的变化,如夏琼等分析了不同降雨模式下边坡孔隙水压力与入渗深度的变化规律,李涛等研究了强降雨对路堤边坡孔隙水压力及体积含水率的影响,但较少对降雨过程中边坡暂态饱和区的形成与消散进行分析;针对降雨条件下边坡稳定性的研究大多只考虑了土体软化及重度变化的影响,如蒋中明等考虑了极端长时间降雨条件下岩体软化对边坡稳定性的影响,夏元友等运用水气两相流-应力耦合计算方法分析了入渗影响区内土体重度变化对边坡稳定性的影响,但鲜有考虑坡体内土体的非饱和抗剪强度。鉴于此,该文基于非饱和渗流理论,对降雨条件下坡积土边坡的孔隙水压力、体积含水率及暂态饱和区的变化规律进行探讨,并结合非饱和抗剪强度理论对降雨过程中坡积土边坡安全系数的变化规律进行研究。
1 非饱和渗流及抗剪强度理论
1.1非饱和渗流理论
降雨入渗条件下路堤内部非饱和区土体中水分的迁移规律与饱和区土体中水分的迁移规律一致,都是自发地从高水势处流向低水势处。因此,路堤内部非饱和区渗流与饱和区渗流一样符合达西定律及其连续性方程:

式中:v为土中水的流速;k(θ)为与体积含水率有关的土的渗透系数;θ为土的体积含水率;H为总水头;W为源汇项;mw为比水容量;ρw为水的密度;t为时间。
非饱和渗流初始条件为:
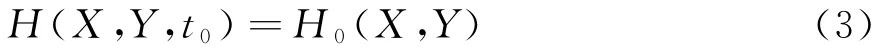
数值计算结合以下边界条件进行:
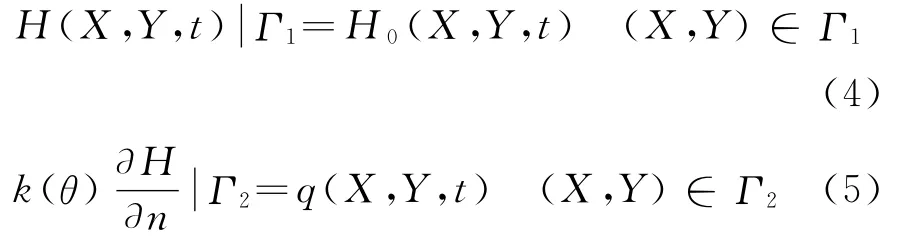
式中:Γ1为水头边界;Γ2为流量边界;q为单位流量;n为边界Γ2所对应的外法线单位向量。
非饱和区土体的渗透系数、体积含水率与基质吸力之间的关系采用Van Genuchten模型进行拟合,模型表达式如下:

式中:θs为饱和体积含水率;θr为残余体积含水率;m、n、α均为Van Genuchten模型拟合参数,m=1 -1/n;ψ为基质吸力;Ks为饱和渗透系数。
1.2非饱和抗剪强度理论
大量边坡失稳现象表明,边坡失稳破坏以剪切破坏为主。库仑最早提出了描述土体抗剪强度的摩尔-库仑破坏准则,该准则虽然反映了土体正应力与抗剪强度之间的关系,但没有体现非饱和土中基质吸力的影响。因此,D.G.Fredlund等于1978年提出了可考虑非饱和土中基质吸力影响的非饱和土抗剪强度计算公式:
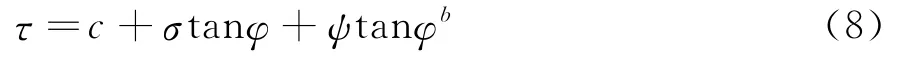
式中:τ为非饱和土抗剪强度;c为粘聚力;σ为正应力;φ为与正应力相关的摩擦角;φb为与基质吸力相关的摩擦角。
2 数值模型与参数
为研究坡积土边坡在降雨条件下的渗流特征及稳定性,以汝郴(汝城—郴州)高速公路某典型坡积土边坡为研究对象,建立图1所示数值模型,并在边坡坡面中点及过中点的水平线上设置一个特征点和一条特征截面。

图1 数值模型网格、特征点及特征截面示意图(单位:m)
(1)渗流边界条件。模型两侧及底部设置为零流量边界,模型顶部设置为单位流量边界。
(2)渗流初始条件。在模型两侧设置总水头为7 m的水头边界,并进行稳态渗流计算,得到初始时刻边坡渗流场(见图2)。

图2 初始时刻边坡渗流场(单位:kPa)
(3)计算参数。在现场取原状坡积土土样进行室内变水头试验,测得坡积土的饱和渗透系数为0.009 35 m/h。同时开展土水特征试验,得到坡积土渗透系数、体积含水率与基质吸力的关系曲线(见图3)。坡积土的力学参数通过三轴抗剪强度试验得到(见表1)。
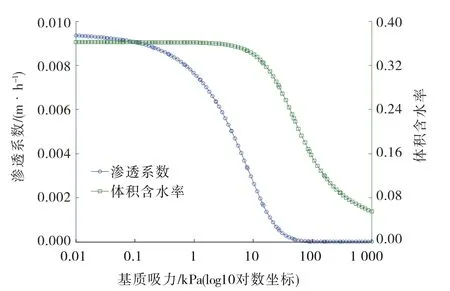
图3 渗透系数与土水特征曲线(单位:m)

表1 坡积土力学参数
(4)分析方案。为了分析降雨强度对坡积土边坡渗流特征及稳定性的影响,设计表2所示3种降雨分析方案。
3 降雨条件下边坡渗流特征与稳定性分析
3.1降雨入渗对边坡孔隙水压力的影响
图4为降雨条件下特征点孔隙水压力随时间的变化。由图4可知:降雨开始后36 h内,不同方案下特征点孔隙水压力均迅速升高,此后(降雨36~96 h内)其升高速率逐渐放缓;降雨停止后,特征点孔隙水压力持续降低。此外,降雨强度越大,同一时刻特征点的孔隙水压力越大。

表2 降雨分析方案

图4 不同方案下特征点孔隙水压力变化规律
图5(a)、(b)分别为降雨条件下特征截面孔隙水压力的三维变化和分布规律示意图。由图5可知:降雨开始后,坡面附近土体的孔隙水压力依次升高,距离坡面越近,其孔隙水压力响应的时间越早,增长幅度也越大;降雨停止后,降雨入渗影响区内土体的孔隙水压力逐渐降低,降雨入渗影响区外一定范围内土体的孔隙水压力则继续增长。此外,降雨过程中,同一时刻特征截面孔隙水压力与降雨强度成正比。
3.2降雨入渗对边坡体积含水率的影响
图6为降雨条件下特征点体积含水率随时间的变化。降雨条件下坡面附近土体的体积含水率很难完全饱和,一般情况下,当土体体积含水率达到饱和体积含水率的85%时,则认为已进入饱和状态。对于坡积土边坡,当体积含水率为0.307 7时即认为已达到饱和状态。由图6可知:降雨开始后36 h内,不同方案下特征点体积含水率均迅速升高,此后(降雨36~96 h内)其升高速率逐渐放缓;降雨停止后,特征点体积含水率持续降低。此外,降雨强度越大,同一时刻特征点的体积含水率越高,达到暂态饱和区所需的时间越短。

图5 不同方案下特征截面孔隙水压力变化规律

图6 不同方案下特征点体积含水率变化规律
图7为降雨条件下特征截面体积含水率的三维变化和分布规律示意图。由图7可知:降雨开始后,坡面附近土体的体积含水率依次升高,距离坡面越近,其体积含水率响应的时间越早,进入暂态饱和区的时间越早,增长幅度越大;降雨停止后,降雨入渗影响区内土体的体积含水率逐渐降低,降雨强度越小,暂态饱和区消散的速率越快,降雨入渗影响区外一定范围内土体的体积含水率则继续增长。此外,降雨过程中,同一时刻特征截面体积含水率及进入暂态饱和区的长度均与降雨强度成正比。

图7 不同方案下特征截面体积含水率变化规律
3.3降雨条件下边坡暂态饱和区变化规律
图8为不同降雨强度下边坡暂态饱和区的变化。由图8可知:降雨开始后,边坡暂态饱和区自坡面往内逐渐扩展,降雨强度越大,边坡暂态饱和区扩展速率越快,所形成的暂态饱和区面积越大;降雨停止后,边坡暂态饱和区自坡顶往坡脚附近迅速消散,降雨强度越大,边坡暂态饱和区消散速率越慢。此外,在降雨强度0.006 61 m/h条件下,由于降雨停止后边坡暂态饱和区内体积含水率较高、面积较大,降雨停止后边坡暂态饱和区面积先小幅度扩展、后迅速消散。
3.4降雨条件下边坡安全系数变化规律
基于非饱和渗流及抗剪强度理论,结合极限平衡法对坡积土边坡在降雨过程中的安全系数进行计算,结果见图9、图10。
由图9可知:降雨开始后,随着雨水的持续入渗,坡面附近土体的基质吸力不断丧失,体积含水率逐渐升高,土体重度增大,边坡安全系数随着降雨过程的持续不断降低;降雨停止后,边坡安全系数随着基质吸力的恢复及雨水的渗出缓慢升高。此外,同一时刻边坡安全系数与降雨强度成正比。
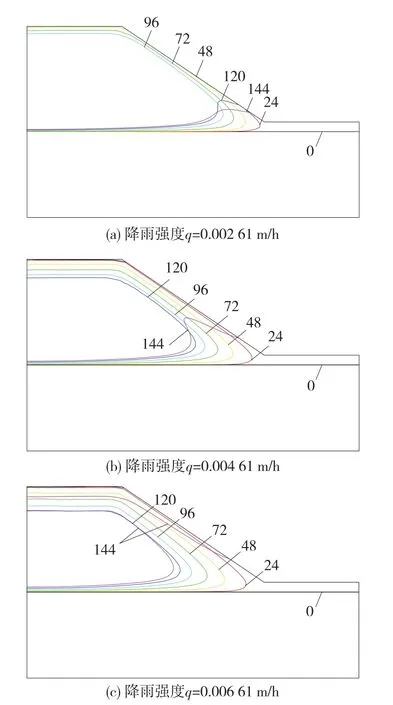
图8 不同降雨强度和时间下边坡暂态饱和区变化规律
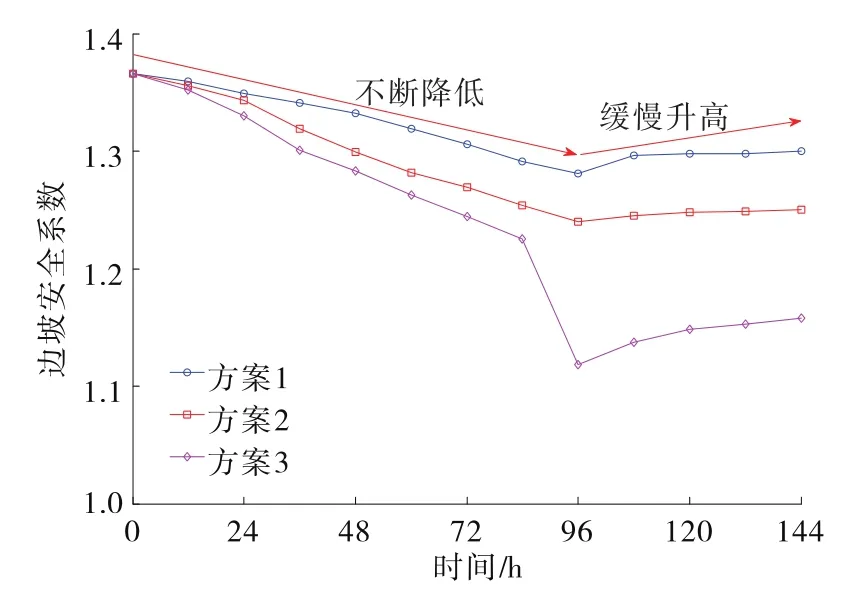
图9 不同方案下边坡安全系数变化规律

图10 降雨96 h后边坡潜在滑动面示意图
由图10可知:降雨强度0.006 61 m/h条件下,降雨96 h时边坡的安全系数仍大于1,其潜在滑动形式为浅层整体滑移。
4 结论
结合非饱和渗流及抗剪强度基本理论,采用数值模拟方法对降雨条件下坡积土边坡孔隙水压力、体积含水率、暂态饱和区及安全系数的变化规律进行分析,得到以下结论:
(1)降雨期间,降雨入渗影响区内土体的孔隙水压力、体积含水率逐渐升高;降雨停止后,坡面附近土体的孔隙水压力、体积含水率持续降低。
(2)降雨条件下,坡面附近土体的孔隙水压力、体积含水率与降雨强度成正比。
(3)降雨开始后,边坡安全系数随着暂态饱和区的扩展不断降低;降雨停止后,边坡安全系数随着暂态饱和区的消散缓慢升高。
(4)降雨过程中,边坡暂态饱和区面积、安全系数均与降雨强度成正比。
[1] 夏琼,窦顺,王旭.不同降雨模式下土质路基边坡渗流场研究[J].铁道工程学报,2014(9).
[2] 李涛,徐伟青,曾铃.强降雨对路堤边坡渗流场及稳定性影响研究[J].公路工程,2013,38(4).
[3] 蒋中明,曾铃,付宏渊,等.极端久雨条件下软岩边坡动态稳定性分析[J].中国公路学报,2014,27(2).
[4] 夏元友,张亮亮.考虑降雨入渗影响的边坡稳定性数值分析[J].公路交通科技,2009,26(10).
[5] 毛昶熙.渗流计算分析与控制[M].第二版.北京:中国水利水电出版社,2003.
[6] 顾慰慈.渗流计算原理及应用[M].北京:中国建材工业出版社,2000.
[7] 蒋中明,唐静,谢刚,等.汝郴高速公路软岩边坡岩体渗透性现场压水试验研究[J].公路与汽运,2010(6).
[8] Papagiannkis A T,Fredlund D G.Asteadystate model for flow insaturated-unsaturatedsoils[J].Canadian Geotechnical Journal,1984,21(3).
U416.1
A
1671-2668(2016)05-0089-05
2016-04-19
