交流伺服进给系统的模型仿真与参数辨识*

王 菲，任 正，罗 忠，柳洪义

(1.东北大学 机械工程与自动化学院，沈阳 110004；2．华晨宝马汽车有限公司，沈阳 110044 )



交流伺服进给系统的模型仿真与参数辨识*

王 菲1，任 正2，罗 忠1，柳洪义1

(1.东北大学 机械工程与自动化学院，沈阳 110004；2．华晨宝马汽车有限公司，沈阳 110044 )

实际生产中各环节的微小变化都将需要伺服系统控制参数的及时调整以保证系统运行的平稳、准确，为便于研究控制参数调整对系统的影响，在分析了交流永磁伺服进给系统一般性组成的基础上，对系统中的机械传动装置、永磁同步电动机及检测反馈器件分别建立了数学模型，并针对市售永磁同步电动机的非开放性进行了基于实测数据的速度控制模型参数辨识，所得到的电动机参数经过验证证明了该辨识方法的可行性。搭建了交流永磁伺服进给系统的整体仿真模型，并进行了仿真实验，仿真实验结果与实测结果吻合，证明了该模型的正确性。

交流伺服进给系统；交流永磁同步电动机；模型仿真；参数辨识

0 引言

随着工业4.0的发展，工厂自动化进程不断加快。与此同时，作为以数控机床、加工中心、工业机器人为制造主体的柔性自动化加工的基础，对交流伺服进给系统的精确控制成为实现柔性自动化加工的关键技术之一[1]。

Chunjie Zhou等研究了基于网络化电子加工服务的交流永磁同步电动机远程控制方法[1]，设计了电动机的改进的自适应模糊控制器，针对网络化制造中存在的负载波动下的不确定惯量和摩擦问题，能够实现基于网络的远程高精度电动机驱动控制，保证了网络化制造设备伺服进给系统的精度。孙军等对工业加工中普遍使用的交流伺服进给系统进行了分析[2-4]，对系统中永磁同步电动机的控制及机-电联合模型的建立等问题进行了研究，并进行了仿真，为提高交流伺服进给系统的控制精度提供了理论依据。

然而通常情况下使用的交流伺服电动机是不完全对用户开放的，电动机驱动器的参数不完全已知，使伺服进给系统的模型不能被准确建立。本文针对电动机驱动器的参数不完全已知的情况，在分析了交流伺服进给系统组成的基础上，建立了系统的数学模型及方框图，提出了在系统中存在封闭的交流永磁同步电动机及其驱动器时的伺服系统速度环控制参数进行辨识的方法，对一定负载下的进给系统进行了仿真实验，验证了所建立模型及参数辨识结果的正确性。

1 交流伺服进给系统模型

不同的交流伺服进给系统通常具有不同的形态，但他们大多可简化为如图1所示的结构[5]。主要由交流永磁同步伺服电动机、功率逆变器、检测及反馈单元、PWM生成电路、电流控制器和速度控制器、机械传动装置等组成[6]，如图2所示。

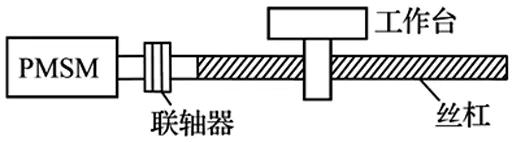
图1 机械传动示意图

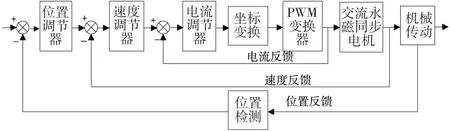
图2 交流伺服进给系统原理图

在图2所示的位置伺服系统中，由光栅尺的位置检测、比较器和位置调节器来构成系统外部的位置环；速度环在伺服电动机驱动器内部闭合，由光电编码器、比较器和速度调节器构成；电流环同样在伺服电动机驱动器内部闭合，由电流传感器、比较器、电流调节调节器和脉宽调制单元组成。

1.1 机械传动装置动力学模型

假设联轴器近似等效为刚性联接，忽略滚珠螺母的质量及非线性摩擦，图1所示的机械传动系统的动力学模型如图3所示[7]。

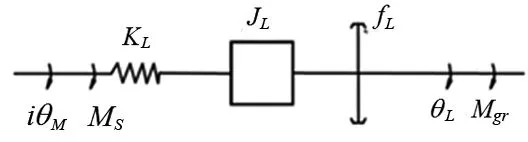
图3 机械传动系统动力学模型

其中， KL、JL、fL、Ms、Mgr为机械传动部件折算在丝杠上的扭转刚度、转动惯量、粘性阻尼系数、总转矩及干扰转矩，i为电动机与丝杠之间的传动比，θM、θL分别为丝杠的输入端和输出端转角。

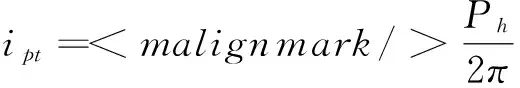
(1)

以电动机的输出角位移为系统的输入，工作台的位移为系统的输出，机械传动装置的框图，如图4所示。

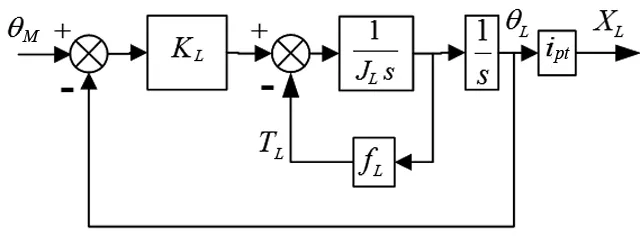
图4 机械传动系统框图

1.2 交流永磁同步电动机数学模型

在d-q坐标系下，定义TL为负载转矩， Be为粘滞摩擦系数，J为电动机与负载的转动惯量之和，pm为转子极对数，ωm为转子机械角速度， Rs为电枢绕组电阻，ψf为转子磁钢在定子绕组上的耦合磁链，d、q轴电感相等为L， ud、uq、id、iq分别为d轴和q轴上的等效电枢电压及电流分量。交流永磁同步电动机的状态方程为[8]：

(2)

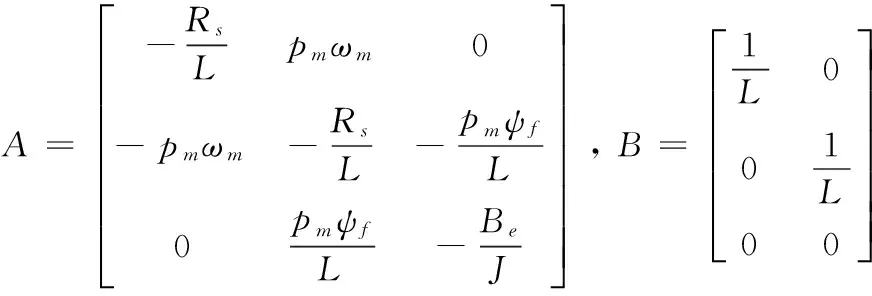
永磁同步电动机通常采用id=0的矢量控制方式，此时的电动机状态方程为[8]：

(3)

此时三相永磁同步电动机的输出转矩为：

Te=pmψfiq=KTiq

(4)

以电压uq、转子角速度ωm分别为系统的输入、输出，电动机系统框图如图5所示。

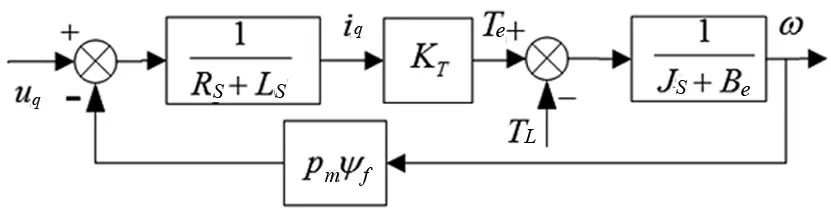
图5 交流永磁同步电动机系统框图

1.3 检测及调节环节的数学模型

位置检测单元、位置调节器、速度检测单元、速度调节器可由式(5)～(8)表示[9]。

PL(t)=KpfXL(t)

(5)

Uc(t)=Kp[PP(t)-PL(t)]

(6)

(7)

UM(t)=Kv[Uc(t)-Ug(t)]

(8)

式中，PL(t)、PP(t)分别为位置反馈和指令脉冲数，XL(t)为工作台位移，Kpf、Kωf为位置、速度反馈增益， Uc(t)、Ug(t)为位置环的指令及反馈电压， Kp、Kv为位置、速度放大器的增益， θM(t)为电动机轴转角， UM(t)为电枢回路输入电压。

综上，建立整个交流永磁伺服进给系统的数学模型，如图6所示。

图6 伺服进给系统的数学模型

2 交流伺服系统的速度控制模型参数辨识

2.1 速度控制模型参数辨识

由图6可知，交流永磁伺服系统速度控制模式的系统闭环传动函数为：

(9)

即我们将交流永磁同步电动机简化成一个二阶的系统。

通常，市售的交流伺服电动机都不具有开放性，只提供电动机的部分参数[10]。以某交流永磁伺服电动机为例，其提供了电动机的转动惯量、电枢电感、定子电阻等参数，但转子磁场等效磁链ψf以及速度环的反馈系数Kωf是未知的。要得到速度控制部分的准确模型需要对电动机的部分参数进行辨识。

对实验电动机的控制模式和控制参数进行必要的设定后，给系统输入转速200rad/s，并进行采样。采样结果如图7所示。

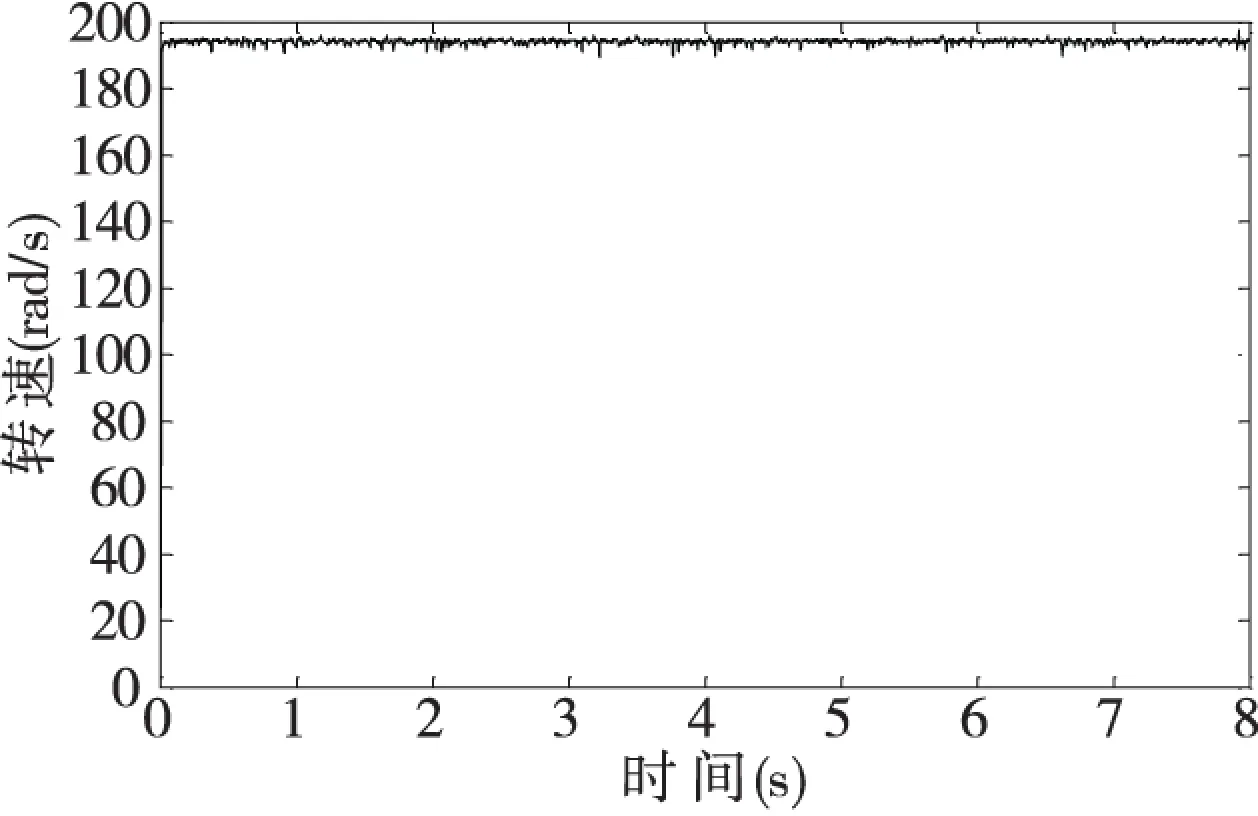
图7 速度信号采样结果

对采样数据作滤波处理后，利用Matlab中的系统辨识工具箱对已假设为二阶系统的交流永磁伺服电动机进行参数辨识。辨识结果为

(10)

结合已提供的电动机的部分参数及式(9)通过待定系数法即可得到该电动机的未知参数。

该例中，经过辨识可得电动机的速度环反馈系数Kωf=0.000629V·s/rad，转子磁场的等效磁链ψf=0.100432Wb，转矩系数KT为KT=pmψf=4×0.100432=0.401728N·m/A。

2.2 速度控制模型仿真验证

根据辨识结果，在Matlab SIMULINK 中建立交流永磁伺服系统速度控制模式的仿真模型，如图8所示，其仿真结果如图9所示。

图8 速度环仿真模型

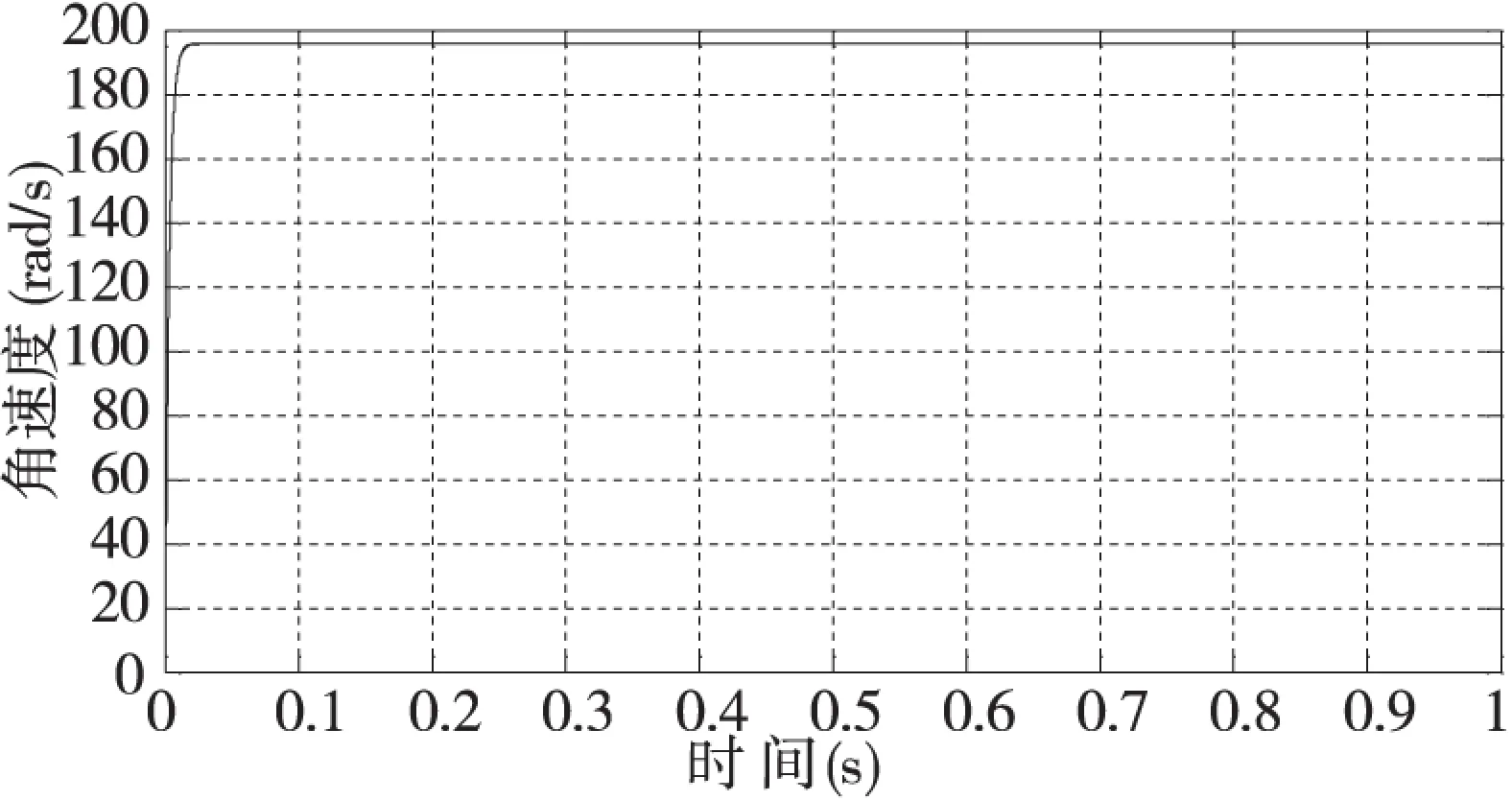
图9 速度环仿真结果

比较图7与图9，可见基于辨识结果的交流伺服系统在0.02s达到了系统的稳态值195.72，系统输出的实测稳态值为192.74，两者相差2.98，相对误差值为1.49%。因此，辨识得到的参数是可行的。

3 交流永磁伺服进给系统模型及仿真

在Matlab SIMULINK里建立系统的仿真模型，如图10所示。给定系统输入为2500脉冲，此时工作台的位置输出应为5mm。模型仿真得到的工作台位置响应和伺服电动机的速度响应如图11和图12所示。

图10 永磁伺服同步电动机进给系统仿真模型

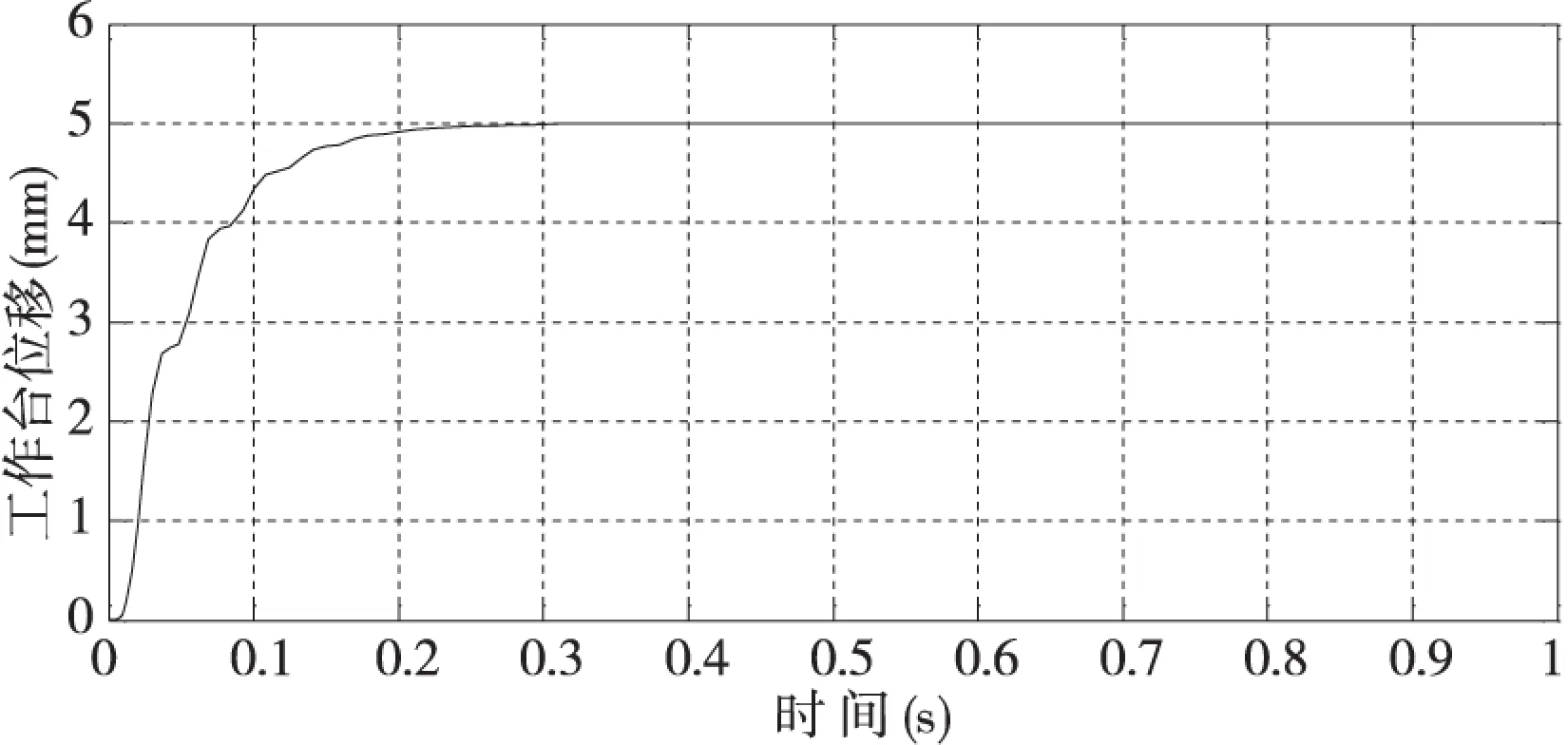
图11 工作台的位置响应

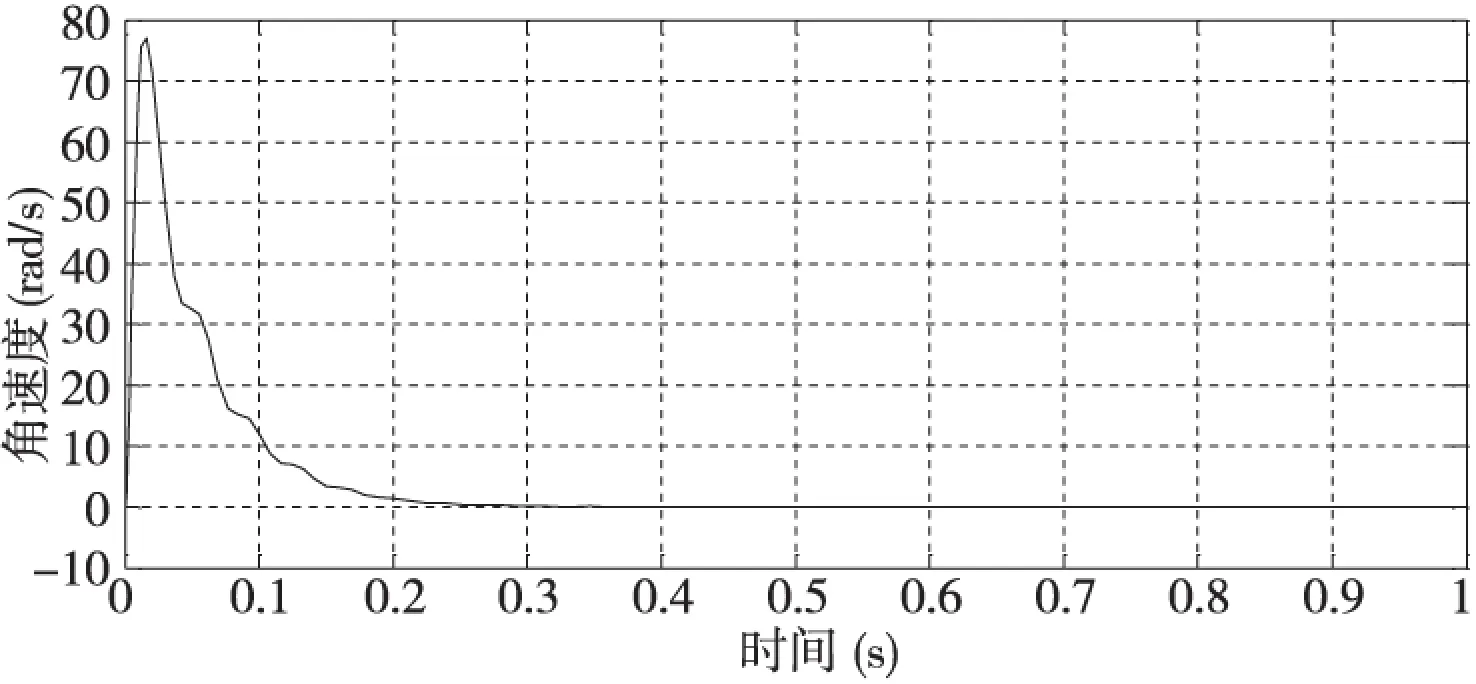
图12 伺服电动机的速度响应

由图11、图12可以看出，系统大约需要0.3s达到稳态值5mm，伺服电动机的峰值约为76.9rad/s，并且在0.3s时电动机的转速下降至0rad/s。与实际交流伺服进给系统的输出吻合，说明仿真模型正确。

4 结论

(1)分析了交流伺服进给系统的基本组成和一般形式，进行了伺服进给系统数学模型的搭建。

(2)在交流永磁同步电动机数学模型的基础上，针对市售的不具有开放性的伺服电动机驱动器，进行了对未知参数的辨识，通过对模型输出和实测数据的对比验证了辨识结果的可行性

(3) 利用MATLAB对所建立的伺服进给系统模型进行仿真实验，实验结果与预期结果相符，证明了模型的正确性。

[1] Chunjie Zhou, Duc-Cuong Quach, Naixue Xiong, et al. An improved direct adaptive fuzzy controller of an uncertain PMSM for web-based e-service systems. IEEE Transactions on Fuzzy systems, 2015 ,23(1): 58-71.

[2] 孙军, 马玲, 张家亮,等. 数控进给系统建模与动态特性分析[J]. 机械与电子, 2016, 34(2): 38-41.

[3] 刘丽伟, 张小杰, 丁圆圆,等. 永磁同步电机的交流伺服控制系统仿真[J]. 计算机仿真, 2015(2): 261-264.

[4] 叶翠青, 汪木兰, 左健民. 基于交流伺服控制系统的数控平台仿真[J]. 组合机床与自动化加工技术, 2013(12): 90-93.

[5] 孙军, 刘伟, 田龙,等. 基于SIMULINK 的伺服进给系统仿真模型与分析[J]. 组合机床与自动化加工技术, 2013(3): 80-83.

[6] 王天宇, 龚邦明. 基于PC运动控制板卡的交流伺服控制系统实验平台设计与实现[J]. 机床与液压, 2013,41(19): 97-99.

[7] 宋玉, 陈国鼎, 马术文. 交流伺服进给系统数学模型研究及其仿真[J]. 机械, 2010,37(7): 33-36.

[8] 寇宝泉, 程树康. 交流伺服电机及其控制[M]. 北京:机械工业出版社, 2008.

[9] 宋玉. 机床伺服控制性能及动态特性研究[D].成都：西南交通大学，2010.

[10] 陈涛. PMSM控制系统参数辩识的建模与仿真[J]. 计算机仿真, 2011,28(2): 240-243.

(编辑 李秀敏)

Modeling & Simulation of AC Servo Feeding System and Parameter Identification

WANG Fei1, REN Zheng2, LUO Zhong1, LIU Hong-yi1

(1.School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China；2.BMW Brilliance Automotive Ltd, Shenyang 110044, China)

To guarantee the smooth and precise operation of an AC servo system, the controller’s parameter should be adjusted in time, while some tiny change happened in the system. For the purpose of facilitating the study on how the adjustion affect the whole system, a model of permanent magnet AC servo feeding system is established in this paper. On the basis of analysis of an AC servo feeding system’s normal structure, the model of each component, including mechanical transmission, PMSM and detection & feedback device, is established respectively. As the incomplete open of the PMSM, an identification method, based on data of actual measurement, for the velocity control loop’s parameter is proposed. Comparing the simulation and actual data, the identification method is proved to be proper. The entire simulation model of the AC Servo feeding system is established. The simulation results well match the actual situation, and verify the validity of the model established in this paper.

AC servo feeding system;PMSM;modeling & simulation;parameter identification

1001-2265(2016)10-0000-00

10.13462/j.cnki.mmtamt.2016.10.000

2016-05-12；

2016-06-17

国家自然科学基金资助项目(11572082)；教育部基本科研业务费专项资金资助项目(N150304004，N140301001)

王菲(1981—)，女，山西晋中人，东北大学硕士研究生，研究方向为机电一体化、工业机器人技术，(E-mail) feiwang@mail.neu.edu.cn。

TH16；TG506

A