蜿蜒河流的数学刻画及其自组织*

汪富泉

（广东石油化工学院继续教育学院，广东茂名525000）

蜿蜒河流的数学刻画及其自组织*

汪富泉

（广东石油化工学院继续教育学院，广东茂名525000）

为探讨蜿蜒河流河床演变中的自组织，应用微分几何方法建立了河道基本单元的数学模型，并通过求解数学模型得到了拐点坐标。根据实测资料和数学模型，绘制了下荆江在近500年间的5次河道轴线变化趋势及拐点分布，观察其变化趋势发现拐点的平面坐标是慢弛豫变量，拐点间距分布具有赫斯特效应，河道平面形态具有分形特征。由此探讨了河床演变中的自组织临界性及河型转换的内外部根源。

蜿蜒河流；下荆江；河床演变；自组织

蜿蜒河流在世界上分布广泛，对人类的生存和发展具有重大影响，关于其演变规律的研究一直受到研究者的高度重视。笔者最近对蜿蜒河流进行了系统研究：计算了蜿蜒河流的量规维数，探讨了它们与河床演变的关系［1］；应用分形方法探讨了河湾之间的相互作用［2］；根据理论和实测资料分析了水动力轴线的非线性变化、流域来水来沙的随机性和河流自身的能量耗散性对我国典型蜿蜒河流下荆江河床演变的影响［3－5］，建立了一个计算蜿蜒河道自仿射性的算法，并由此探讨了下荆江河道的横向摆动特征［6］；在总结前人和自己研究成果的基础上，提出了河流动力系统关联、协同、自适应等6个自组织原理［7］。如何定量描述河床演变的自组织则是一个新的研究课题。本文将运用微分几何方法分析蜿蜒河流局部的数学模型，通过数学模型来计算河流轴线的拐点，并分析拐点坐标的变化特征，然后应用所得理论结果对下荆江500多年来河床演变的自组织进行探讨。

1 蜿蜒河流的数学刻画

蜿蜒河流的中心线（轴线）实际上是一条球面曲线，将其投影到一个固定平面（如海平面）上，得到一条平面曲线C，C的摆布方式则称为蜿蜒河流的平面构象。一般来说，该平面构象比较复杂，通常具有弯曲折叠的几何形状，因此难以写出这条平面曲线的具体方程。如果考虑到它的精细结构（分形结构），那么它的局部也难以用解析式表达。但是，分析平面曲线的局部结构可以发现其规律：它由一系列正反相间的河湾和介于其间的较为顺直的过渡段组成［8］，即两个正反向间的河湾和顺直段是组成平面构象的基本单元。如果我们忽略基本单元的某些细节（如在一定比例尺的地形图上所看到的形状），则可用微分几何［9］方法刻画基本单元的结构。设C的矢量式参数方程为：

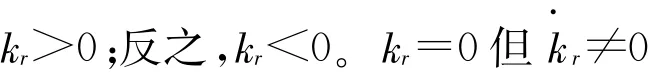
在基本单元上实测4个点，设其坐标为｛（xi，yi）∶i＝0，1，2，3｝，则可得变量为a，b，c，d的四元一次方程组，如下所示：

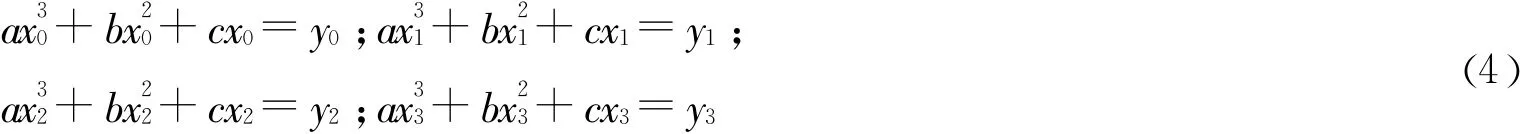
解上述四元一次方程组得a，b，c，d的值，代入（3）得基本单元的数学模型。由微分几何知曲线（3）的相对曲率为：

2 应用示例

位于长江中游的下荆江，其河道中心线（轴线）蜿蜒曲折，是典型的蜿蜒河流。谢鉴衡给出了下荆江近500年的5次河道地形图［8］，笔者用上述数学模型绘制的这5次河道轴线与拐点分布见图1。

通过图1可以发现，1490—1644年下荆江河道轴线上的大部分拐点（见图中标记4～6、10～13、15～17）的平面位置均与其余4个时期的拐点相去甚远。1975年河道轴线的部分拐点（如a，b，c，d，e，f）也有不同程度的偏离。相比之下，在1835—1959年，除河湾蠕动和裁弯增减的拐点外，各轴线的拐点基本上是成团分布的，拐点平面位置的变化很小。拐点附近的河段，即两个旋转方向相反的抛物型河湾间过渡段的位置变化也较小，这说明拐点的平面坐标是慢弛豫变量［10］。它有两层含义：其一，拐点坐标随时间变化较缓慢，如1835—1959年这段时间就是如此；其二，当系统发生突变（即拐点偏离原来位置较远）以后，要恢复到它原来的位置则需要相当长的时间，例如1490—1644年与其它时期相比较，清楚地说明了这点。Hacken［10］在协同学中，根据状态参量在相变（突变）过程中所起的作用，把它们分成两类：快弛豫参量和慢弛豫参量。后者为数极少（往往是一个或几个），但是却主宰着系统的演化和结局，原因在于它们是集体变量，是子系统合作的产物，相变过程的边界条件适合其发展。慢弛豫变量的涨落易得到子系统的响应，从而席卷整个系统，使系统的序或状态发生改变，所以慢弛豫变量也就是序参量。河流系统的序结构是一种自组织结构，Rodriguez Iturbe［11］，Sapozhnikov等［12］都曾从自组织角度研究过河流和地貌的演化，笔者认为他们的论证都有值得商榷的地方。下面笔者通过理论分析和数据计算来检验下荆江河床演变中的自组织特征，并由此推测下荆江河型突变的诱因。

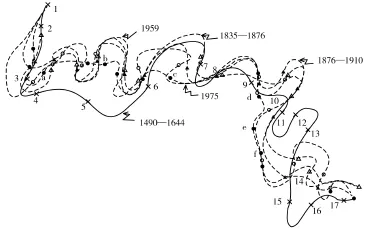
图1 下荆江河道中心线近500年的变化及拐点分布

林一山［13］收集分析了下荆江一千多年的河道资料，认为藕池决口对下荆江蜿蜒河道的形成起决定作用。林承坤等［14］认为围垦堵塞穴口导致河道内流量增加是决定性因素。笔者认为决定性因素是系统内、外部诸要素的非线性相互作用，而外部作用如洞庭湖顶托或人类活动则是导致下荆江河型突变的触发力量［3］。外界的一个扰动使它附近的拐点产生一个偏离，在河流系统内外部因素作用下，这种偏离得到整个河床系统各河湾的响应，使大多数拐点产生了较大的偏离，并促进河湾不断发育，从而导致了河型的转变。一个局部的涨落为什么能够得到整个河段的响应呢？从系统自组织出发可能较好地回答这一问题。河型转变以后，由于河湾个数和形态的变化，不仅拐点的位置发生了变化，相邻拐点的间距也发生了改变，为此，笔者引入了拐点间距进行量化分析。用〈R2i，i＋n〉表示第i和第i＋n个拐点之间距离的平方。当n＝1时，有：

给定一系列d0值，可根据河道地形图的测量结果计算出p（di，i＋1＞d0），在双对数坐标系下做线性回归可得到q值，根据图1的实测资料和式（8）得到的q值如表1所示。

另一方面，蜿蜒河道的平面形态可看成一个物理粒子在正方形点阵上作自回避随机行走（SARW）得到的轨迹。SARW与普通随机行走的区别是粒子有记忆性，走过的路不再重复，因此其轨迹是一条无圈的蜿蜒曲线，蜿蜒河流的轴线正是这样的曲线。描述SARW的数理模型是分数布朗运动，其特征是赫斯特（Hurst）指数H（0＜H＜1）［15］。H＝0.5时，序列相互独立；H＞0.5时，序列具有持续性，H越大，持续性越强；H＜0.5时，序列具有反持续性，H越小，反持续性越强。H和q的关系如下：H＝1/q，此外H与河道平面形态的分形维数df的关系如下：df＝2－H［16］。下荆江河道中心线拐点分布计算结果如表1所示。

表1 下荆江河道中心线拐点分布特征

下荆江是由许多单元组成的复杂系统。在表1中，均有H＞1/2，这说明下荆江河湾之间关系密切，具有复杂的内部非线性相互作用和长程相关性，与笔者最近的研究结果［2］一致。1975年，河道轴线拐点分布的非均匀系数最大，H指数最小，这说明河湾之间的长程关联不如其它时期密切，但非线性相互作用更强烈，这可能与下荆江河道在70年代发生的人工和自然裁弯有关［4］。1490—1644年，河道轴线的γ值较大且H值远大于1/2，河湾之间同时存在较强的长程关联和较强的非线性相互作用［2］。这样就不难理解为什么河道在该时期的变化较大，且和其它时期的平面形态相比具有明显的界限。此外，河流与水系具有分形特征［1－2，6］，这里的Hurst效应和分形特征揭示了河道各河湾相互作用所形成的自组织。

3 结果与讨论

归纳起来，本文得到如下结果：（1）拐点的位置（坐标）是慢弛豫变量，这种随时间缓慢变化的特性实质上等价于负幂律分布，其频谱分布则具有1/f噪声的特征。（2）赫斯特（Hurst）指数H与分形维数有关，这说明河道平面形态具有空间分形结构。（3）以d0为尺度，相邻拐点间距分布满足式（8）。因此，在河湾的形成和发展中，总是大河湾数量少，小河湾数量多。由这三点和Bak等人［17］提出的自组织临界性理论知，下荆江河床作为一个系统处于自组织临界状态。水流动力轴线的非线性特征对河床起着调制作用［3］，流域因素和水力输沙条件的随机性对系统起着扰动作用［4］。此外，系统外部对系统的干扰如洞庭湖顶托及人类活动等也不可忽略。对于自组织临界系统而言，扰动是系统突变的触发力量。一个局部的扰动可使整个系统得到响应，产生多米洛骨牌倒塌那样的连锁反应。因此，洞庭湖顶托和人类围垸堵穴等对河床自组织临界状态的扰动，是下荆江河型转变的诱因。当它们对河床产生扰动时，不同尺度的河湾都可能形成，各个部分之间的协同作用相当于一种正反馈，促使河床形态逐渐由微弯型向蜿蜒型发展。由此可见，外界的干扰是扰动河床系统的一种随机力，是一种直接诱因（外因），而内在原因是河流系统处于自组织临界状态，两者缺一不可。这样能更好地理解为什么上、下荆江河型原来均为微弯型，水力输沙条件、河床物质组成基本相同，而自明清以后，下荆江经过突变而转换为蜿蜒型河道这一段疑难问题。

［1］汪富泉.蜿蜒河流的量规维数与河床演变［J］.水利水电科技进展，2014，34（3）：12－15.

［2］汪富泉.河湾相互作用的分形法研究［J］.水动力学研究与进展，2014，29（2）：205－211.

［3］汪富泉.下荆江蜿蜒河道分形弯曲的物理机制探讨——Ⅰ.非线性机制［J］.广东石油化工学院学报，2014，24（1）：67－71.

［4］汪富泉.下荆江蜿蜒河道分形弯曲的物理机制探讨——Ⅱ.随机性［J］.广东石油化工学院学报，2014，24（4）：51－54，59.

［5］汪富泉.能量耗散对蜿蜒河流分形结构的影响［J］.广东石油化工学院学报，2015，25（1）：63－66.

［6］汪富泉.自仿射曲线分形标度指数的算法及其应用［J］.工程数学学报，2014，31（5）：728－732.

［7］汪富泉.河流动力系统的自组织原理及机制探讨［J］.水利水电科技进展，2014，34（4）：1－4.

［8］谢鉴衡，丁君松.河床演变及整治［M］.北京：水利电力出版社，1990.

［9］梅向明.微分几何［M］.北京：高等教育出版社，1981.

［10］Hacken H.Advanced Synergetics，An Introdunction［M］.2nd ed.Berlin：Springer，1987.

［11］Rodriguez I，Marnani IM，Rigon R，et al.Self－organized River Basin Landscapes：Fractal andMultifractal Characteristics［J］.Water Recources Res，1994，30（12）：3531－3539.

［12］Sapozhnikov V B，Foufoula G E.Do the Current Landscape EvolutionModels Show Self－organized Criticality？［J］.Water Recources Res，1996，32（4）：1109－1112.

［13］林一山.荆江河道的演变规律［J］.人民长江，1978（2）：2－10.

［14］林承坤，陈钦鉴.下荆江自由河曲形成与演变的探讨［J］.地理学报，1959，25（2）：156－168.

［15］刘新有，何大明.怒江流域悬移质输沙时空分布特征及变化趋势［J］.地理学报，2013，68（3）：365－371.

［16］汪富泉，李后强.分形——大自然的艺术结构［M］.济南：山东教育出版社，1996.

［17］Bak P，Tang C，Wiesenfeld K.Self－organized criticality［J］.Phys.Rev.A.，1988，38（1）：364－374.

Mathematical Characterization of Winding River and Its Self－organization

WANG Fuquan
（College of Continuing Education，Guangdong University of Petrochemical Engineering，Maoming 525000，China）

To explore self－organization in bed evolution of winding rivers，differential geometrymethod is applied to establish themathematicalmodel of basic unit，solvingmathematicalmodel to get inflection point coordinates.The Lower reach of Jingjiang in nearly 500 years with five axis change trend and inflection point distribution is drawn according to themathematicalmodel and themeasured data.Observing its change trend，the author finds out that plane coordinate of the turning point is slow relaxation variables，inflection point distribution shows the Hurst effect，and channel planemorphology has fractal characteristics.Thus the author discusses the self－organized criticality of riverbed evolution and river pattern conversion of internal and external causes.

Winding river；Lower Jingjiang；Fluvial process；Self－organizations

TV147

A

2095－2562（2016）01－0065－04

（责任编辑：梁晓道）

2015－08－15；

2015－11－02

国家重点基础研究发展计划（973计划）（2013cB036401）；国家自然科学基金（51179110）

汪富泉（1955—），男，四川南充人，博士，教授，主要从事水文学及河流动力学研究。