粒子群优化小波神经网络的齿轮箱故障诊断

杨柳 李志农

(武汉工程大学机电工程学院)(南昌航空大学无损检测技术教育部重点实验室)

粒子群优化小波神经网络的齿轮箱故障诊断

杨柳*李志农

(武汉工程大学机电工程学院)(南昌航空大学无损检测技术教育部重点实验室)

针对传统的小波神经网络容易陷入局部极小、收敛速度慢和运行效率低等不足，将粒子群优化引入小波神经网络中，提出了一种粒子群优化小波神经网络学习算法。该方法利用粒子群算法优化小波神经网络中的权值(即尺度因子)和阈值(即平移因子)，从而可以自适应地选择小波神经网络的参数，提高算法的收敛性和快速性，克服传统的小波神经网络容易陷入局部极小、收敛速度慢和运行效率低等不足。实验结果表明，提出的方法是有效的，优于传统的小波神经网络学习算法，能够准确地识别齿轮裂纹的损坏程度。

粒子群 故障诊断 小波神经网络 齿轮箱 齿轮裂纹

0 引言

小波神经网络是基于小波变换而构成的神经网络模型，即用非线性小波基取代通常的神经元非线性激励函数(如Sigmoid函数)，相应的输入层到隐含层的权值及隐含层的阈值分别用小波函数的尺度伸缩因子和时间平移因子来代替，把小波变换与神经网络有机地结合起来，既继承神经网络的自学习、自适应、容错性、鲁棒性和推广能力，同时又具有小波变换特有的变焦特性和时频局部特性。基于小波神经网络的独特优势，小波神经网络在机械故障中获得了成功的应用[1]。然而，随着问题的研究深入，传统的小波神经网络在故障诊断的应用中存在的不足也充分暴露出来。当特征维数增加时，网络输入维数随之增加，这必然造成网络训练的样本呈指数增长，网络结构也随之变得庞大，使得网络的收敛速度大大下降。另外，在传统的小波神经网络中，小波网络中初始化参数也是一个大的问题，若尺度参数(即权值)和平移参数(即阈值)初始化不合适，将导致整个网络学习过程的不收敛，容易造成运算量大、收敛速度慢、陷入局部极小的缺点。因此，针对传统小波神经网络存在的问题，有必要寻求新的有效的方法来改进传统的小波神经网络学习算法，以增强该网络的灵活性和自适应性[2]。

粒子群优化算法（particle swarm optimization, PSO)是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。该优化算法具有很强的通用性，优化函数时，不需要计算函数的梯度信息，也不要求目标函数和约束的连续性、可导、凸性、可行域联通，甚至有无解析表达式，只需要依据适应度函数，通过粒子的位置和速度更新公式进行更新来优化函数。粒子算法本身需要调整的参数少，策略简单，因而便于操作、易于实现，相对于传统的梯度递减优化算法表现出很大的优势。基于粒子群优化算法的独特优势，在此将该算法引入到传统的小波神经网络中，提出了一种粒子群优化的小波神经网络算法，并应用到齿轮箱的齿轮裂纹故障诊断中。同时，与传统的小波神经网络方法进行了对比分析。本文的研究为整个齿轮传动系统的检修方案提供了一种有效的方法，具有重要的参考价值[3]。

1 小波神经网络

小波神经网络由三层神经网络组成，即输入层、隐含层和输出层，每一层神经元的数目不同，它采用非线性小波基函数作为隐含层的激活函数。本文将Morlet小波作为隐含层，Sigmoid函数作为输出层的激活函数。小波神经网络结合了小波分析和神经网络的优点，在模式识别、故障诊断和信号处理等领域中广泛应用[4]。Morlet小波和Sigmoid函数分别如式（1）和式（2）所示：

小波神经网络模型如图1所示。图1中，x1，x2，x3，…，xi为输入层，y1，y2，y3，…，yn为经过网络训练后的输出向量，I，J，N分别是输入层，隐含层，输出层的节点数，wij为输入层和隐含层的连接权值，wjn为隐含层和输出层的连接权值。

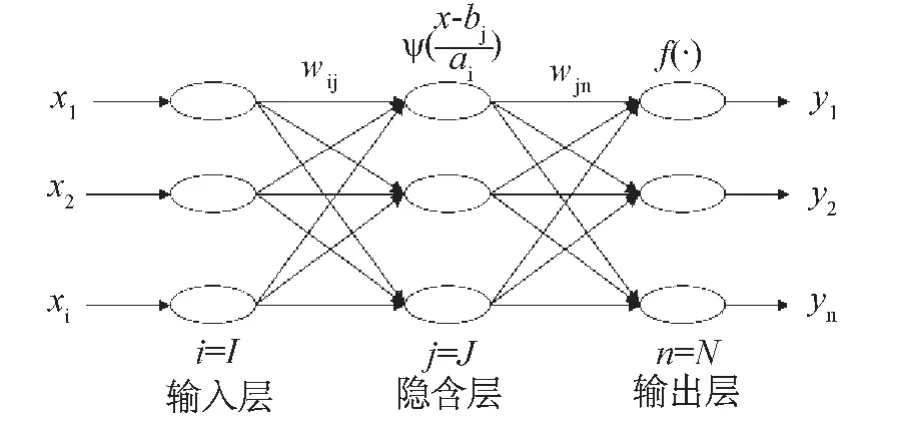
图1 小波神经网络

2 粒子群优化小波神经网络

2.1 基本粒子群优化算法

粒子群算法初始化一群随机粒子，也称之为随机解。在一个D维的目标搜索空间之中，有M个粒子组成一群落X，X表示为X=(X1，X2，X3，…，XM)。将第i个粒子的当前位置表示为Xi=（Xi1，Xi2，Xi3，…，XiD），第i个粒子的速度Vi= (Vi1，Vi2，Vi3，…，ViD)，其中i=1，2，3，…，M。根据Xi的目标函数可以得出适应值，由所得到的适应值可以确定第i个粒子当前的优劣。第i个粒子的个体极值计为Pi=(Pi1，Pi2，Pi3，…，PiD)，整个粒子群搜索到的种群全局极值为Pg=(Pg1，Pg2，Pg3，…，PgD)[4]。基本粒子群优化算法的更新公式如下：

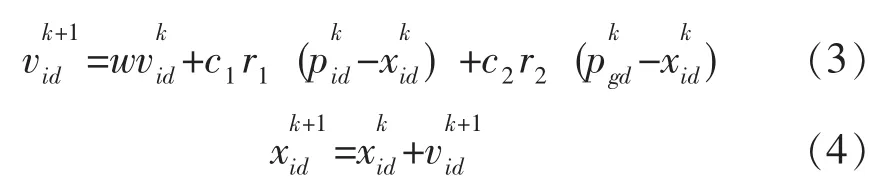
式中k——迭代次数，i=1，2，3，…，M；

d=1，2，3，…，D；

c1、c2——加速度常数，c1是调节粒子向自己的最佳位置移动的学习因子，c2是调节粒子向全局最佳位置移动的学习因子；

r1、r2——[0，1]之间的相互独立的随机数；

w——惯性权重因子；

wmax、wmin——分别为w的最大值和最小值；

Iter、MaxIter——当前迭代数和最大迭代数。

粒子在每一维的飞行速度不能超过设定的最大速度Vmax。当Vmax设置为较大时，粒子群的全局搜索能力很强；当Vmax较小时，粒子群的优化算法局部能力较强。达到了最大迭代次数或粒子群搜索的最优位置满足最小适应阈值设定值时，迭代终止。

2.2 粒子群优化小波神经网络学习算法流程

定义粒子群的位置向量X的元素为小波神经网络各层间连接权值以及伸缩平移参数a和b，适应值函数为小波神经网络的均方误差函数为:

式中N——输出的节点数；

Di——第i个输出节点的目标值；

Yi——第i个输出节点的实际值[5]。

粒子群优化小波神经网络算法流程如下：

（1）设置小波网络参数的初始值，伸缩因子a，平行因子b，其余网络权值初始值设为（0，1）间的随机数。

（2）初始化粒子群的各个参数：粒子数设为m，适应阈值ε，w的最大值、最小值设定为wmax、wmin；加速因子设为c1、c2，最大允许迭代步数MaxIter；粒子的速度V，位置X，初始化为（0，1）之间随机数。

（3）粒子个数m，随机生成粒子群矩阵。

（4）利用粒子群算法中的式(3)、式(4)对每个粒子的位置X和速度V迭代更新，记录每个粒子的历史最优位置Pid和迄今搜索到的最优位置Pgd，利用式(5)计算适应度值，并记录对应于Pid、Pgd的适应度值FitPid和FitPgd。

(5）判断适应度值是否达到设定值，若FitPgd≤设定值或迭代步数达到了最大设定迭代步数，那么迭代完毕，否则转至步骤（3）。

(6）将Pgd的值代入小波神经网络中伸缩因子a、平移因子b和各个权值之中，计算网络输出[6]。

3 齿轮箱故障诊断实验与分析

实验中所选取的齿轮箱振动信号采集设备系统如图2所示，其中包含水平和垂直方向上的352C67PCB型加速传感器，一台进行数据采集的电脑和一台DSP Siglab型信号分析器。其主要过程是将齿轮箱连接Spectra Quest型动态模拟器对其振动信号进行采集，然后利用信号分析器分析实验采集的信号。

实验中齿轮系统的故障设置为齿轮裂纹：F1为齿轮正常工作状态；F2为25%的裂纹等级故障齿轮；F3为50%的裂纹等级故障齿轮；F4为75%的裂纹等级故障齿轮。在实验过程中，电机的转速为800 r/min，载荷为100%，分别采集F1、F2、F3、F4这4种状态下的各组振动信号数据，每次的采集数据点为8192。将这8192个数据点分为相等的8小段，每段为1024个数据点。对振动信号数据进行相应的变换后提取故障特征参数，分别为均值、标准差、有效值、峰值指标、裕度指标、脉冲指标、峭度指标和波形指标。将采集的数据信号进行归一化，如表1所示。

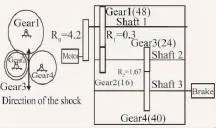
图2 齿轮箱信号采集与分析系统

经过多次实验比较后，选择小波神经网络结构为8-14-4；粒子群的个数为20，加速因子c1=c2= 2，惯性因子w的最大值、最小值分别为wmax=1.5、wmin=0.1，适应阈值ε=0.01，粒子群最大飞行速度为Vmax=1；最大迭代步数MaxIter=5000。

图3 BP算法的误差演化曲线

将表1中的8组训练样本通过粒子群优化小波神经网络进行训练。图3、图4分别为用传统BP算法和PSO算法训练小波神经网络的误差演化曲线，其中横坐标为迭代次数，纵坐标为误差精度。由图3可见，BP算法训练小波神经网络在经过5000次迭代后平均误差还为2.97，说明陷入局部极值。由图4可见，PSO算法训练小波神经网络在经过1536次迭代后，达到设置的误差精度0.01而收敛；在经过600次迭代时，误差精度值为0.86，显然收敛的速度也更快。

表1 齿轮箱振动信号部分特征参数

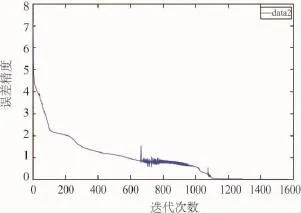
图4 PSO算法的误差演化曲线

把一组检验样本输入训练后的粒子群优化小波神经网络，诊断结果如表2所示。

由表2可知，不论是无裂纹，还是有裂纹，以及裂纹的不同损坏程度，提出的方法都能有效地辨识齿轮裂纹的状态，再次验证了该方法的有效性。

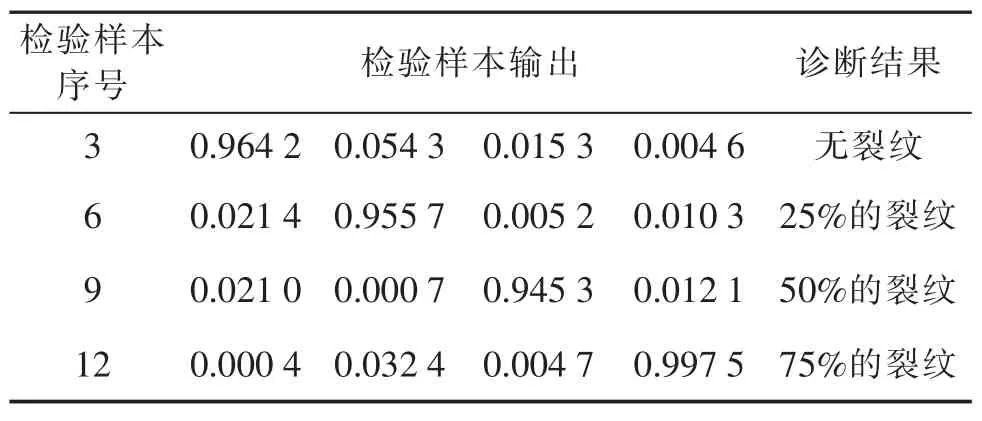
表2 检验样本输出及诊断结果

4 结论

本文将粒子群优化算法训练小波神经网络的方法应用于齿轮箱齿轮裂纹故障诊断。实验结果表明，粒子群优化的小波神经网络能够准确快速地识别出裂纹的损坏程度。粒子群优化算法与传统的梯度递减法相比，减少了迭代次数，提高了误差精度。该方法能够较早发现齿轮裂纹的损坏情况，为整个齿轮传动系统的检修提供很好的指导和参考，也验证了本文提出的粒子群优化小波神经网络对齿轮裂纹故障诊断的有效性。

[1]丁宇新，沈雪勤.基于能量密度的小波神经网络[J].计算机学报，1997，20(9)：832-838.

[2]Chen Hanxin,Lu Yanjun,Tu Ling.Fault identification of gearboxdegradationwithoptimizedwaveletneural network[J].Shock and Vibration,2012:1-16.

[3]张炎.基于粒子群算法和小波理论的机械故障诊断[D].武汉：武汉工程大学，2013.

[4]Kennedy J，Eberhart R C.Particle swarm optimization [C]//Proceeding of the IEEE International Conference on Neural Networks.Ⅳ.Perth:IEEE Press,1995:1942－1948.

[5]Kennedy J.The particle swarm：Social adaptation of knowledge[C]//Proc IEEE Int Conf Evol Comput.1997: 303-308.

[6]王岁花，冯乃勤，李爱国.基于粒子群优化的BP网络学习算法[J].计算机应用与软件，2003，6（8）：74-76.

Fault Diagnosis of Gearbox of Wavelet Neural Network with Particle Swarm Optimization

Yang LiuLi Zhinong

Since the traditional wavelet neural network has the defects of the local minimum,the slow convergence speed and the low operation efficiency,the particle swarm optimization is introduced into the wavelet neural network and the network learning algorithm is proposed.The weight values and the threshold values of the wavelet neural network are optimized through the particle swarm algorithm so that the suitable parameters can be selected,meanwhile,the convergence and rapidity of the algorithm are improved,overcoming the defects of the traditional wavelet neural network.The experimental results show that the proposed method,which can accurately identify the damage of the gear crack,is effective and superior to the traditional wavelet neural network learning algorithm.

Particle swarm;Fault diagnosis;Wavelet neural network;Gearbox;Gear crack

TQ 050.7

10.16759/j.cnki.issn.1007-7251.2016.08.008

2015-11-19）

*杨柳，男，1988年生，硕士，工程师。武汉市，430000。