惯性平台自标定中惯性仪表安装误差可观测性分析*

丁智坚，蔡 洪，张文杰

(国防科技大学 航天科学与工程学院， 湖南 长沙 410073)



惯性平台自标定中惯性仪表安装误差可观测性分析*

丁智坚，蔡 洪，张文杰

(国防科技大学 航天科学与工程学院， 湖南 长沙 410073)

针对惯性平台自标定中惯性仪表安装误差可观测性问题，深入研究了系统模型与平台坐标系对惯性仪表安装误差可观测性的影响。根据不同系统动力学模型和观测量构建四种系统模型。从可观测性定义出发，分析与判断惯性仪表安装误差在不同系统模型和不同平台坐标系下的可观测性。理论分析和仿真结果均表明惯性仪表安装误差在以下两种情况完全可观：观测量为平台框架角和加速度计输出，系统动力学模型为框架角模型，平台坐标系以平台六面体为基准定义；观测量为加速度输出，系统动力学模型为姿态角或失准角模型，平台坐标系以加速度计敏感轴为基准定义。

可观测性；安装误差；自标定；惯性平台

惯性仪表安装误差是高精度惯性平台主要误差源之一，故使用前需对其进行标定与补偿。然而传统的惯性平台多位置自标定[1-2]或多位置静漂[3-4]等方法均无法有效地标定惯性仪表安装误差。

惯性平台连续翻滚自标定技术[5-10]是一种高精度惯性平台自标定方法。通过框架系统控制平台在1g重力场内连续翻滚，利用Kalman滤波技术完成平台姿态角(或失准角)、惯性仪表安装误差以及仪表自身误差等众多误差项的标定与补偿，提高惯性平台使用精度。相对于多位置自标定和多位置静漂自标定方法，连续翻滚自标定技术能够有效地分离出惯性器件安装误差，且标定精度较高，故引起了广泛的研究兴趣。

然而，不同文献[4-11]对惯性平台连续翻滚自标定问题建立了不同的系统模型。其中系统动力学模型有平台失准角模型[5-7]、框架角模型[11]和姿态角模型等多种模型，观测模型存在加速度计输出模型[5-10]和框架角模型[4,11]等不同模型。由不同的动力学模型和观测模型可以构建多种系统模型。而模型的不一致，会造成仪表安装误差的可观性不同。不合适的系统模型会降低仪表安装误差的可观度，甚至导致其不可观。此外，上述文献关于平台坐标系存在两种不同定义：一种以平台六面体为基准定义[11]；另一种以石英加速度计输入轴为基准定义[5]。不同的平台坐标系定义会导致惯性仪表(加速度计和陀螺仪)安装误差矩阵不同，例如加速度计安装误差矩阵，在前者定义方式下存在六项安装误差角，而后者只有三项安装误差角。进而会影响惯性仪表安装误差的可观性。

针对上述两个问题，以惯性平台连续翻滚自标定问题为研究对象，根据不同的系统动力学模型和观测模型建立了四种可行的系统模型。从可观性定义角度出发，以系统唯一解的存在与否为判据，分别分析了惯性仪表安装误差在各个系统模型和不同平台坐标系定义下的可观性。通过仿真对理论分析结果进行了验证。最后，给出了满足仪表安装误差可观的条件。

1 惯性平台自标定模型

1.1 相应坐标系定义

假设惯性平台为三轴平台，其三个单自由度积分陀螺仪和三个石英加速度计以平台六面体为基准安装于惯性平台之上。为了分析问题简便，定义下述坐标系：

1)导航系(n系)：以当地地理系作为导航坐标系，即北-天-东坐标系。

(1)

其中，C表示坐标系之间转移矩阵，I为3阶单位矩阵。

3)以平台六面体为基准定义的平台坐标系(ps系)：以平台六面体三个正交轴为基准，建立平台坐标系。不考虑框架安装误差，当框架均处于零位时，ps系的三个轴与平台三个框架轴平行。

4)以石英加速度计输入轴为基准定义平台坐标系(pa系)：取平台几何中心O为原点；OXpa轴与X石英加速度计敏感轴平行；OYpa轴平行于X和Y石英加速度计敏感轴所确定的平面，并与OXpa轴垂直；OZpa轴与OXpa轴以及OYpa轴构成右手坐标系。

5)加速度计敏感轴坐标系(sa系):该坐标系是非正交坐标系，坐标轴与三个石英加速度计敏感轴平行。

6)陀螺仪敏感轴坐标系(sg系):与加速度计坐标系定义类似，定义sg系三个坐标轴分别与三个陀螺仪敏感轴方向平行。

7)计算平台坐标系(c系)：定义计算机建立的数学平台坐标系为计算平台坐标系，其与平台坐标系之间存在失准角ψ，则c系到p系的坐标转移矩阵为：

(2)

1.2 惯性仪表安装误差矩阵

根据上述定义可以看出，从惯性仪表敏感轴坐标系(sa系与sg系)转到平台坐标系(ps系或pa系)需要经历两个过程：“扶正”和“转动”。其中“扶正”是指将非正交的敏感轴坐标系正交化的过程。定义正交化后的坐标系满足X轴与惯性器件的X敏感轴平行，Y敏感轴与正交化坐标系的XY平面平行。假设所有非正交角均满足小角度假设，根据定义，加速度计和陀螺仪“扶正”矩阵Ta与Tg可表示为：

(3)

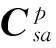
(4)

其中θaC与θgC表示从正交系到平台坐标系的误差角矢量。根据平台坐标系的不同定义，式(4)中的矩阵C(θaC)与C(θgC)有不同的表达式，进而引起仪表安装误差存在不同形式。

1.2.1 平台坐标系(p系)为ps系

当ps系为平台坐标系时，矩阵C(θaC)与C(θgC)为：

(5)

将式(3)、式(4)代入式(5)且忽略小角度乘积，有

(6)

从式(6)中可以看出，当以六面体为基准定义平台坐标系时，加速度计和陀螺仪组件各存在6项安装误差角。

1.2.2 平台坐标系(p系)为pa系

当选择pa系作为平台坐标系时，根据相关定义，C(θaC)与C(θgC)可写为：

(7)

其中上标*用于区分在pa系下和ps系下陀螺仪的非正交安装误差角矢量θgC。

将式(3)和式(4)代入式(7)，忽略小量乘积，有：

(8)

从式(8)中可以看出，当以石英加速度计输入轴为基准定义平台坐标系时，加速度计有3项安装误差，陀螺仪有6项安装误差角。

此外，根据pa系定义和式(5)，有

(9)

忽略小量乘积，有

(10)

式(6)与式(8)反映了惯性仪表安装误差矩阵与平台坐标系定义之间的关系。从中可以看出，平台坐标系定义不同会导致惯性仪表安装误差角个数的不同，进而引起仪表安装误差矩阵的差别。特别地，当pa系为平台坐标系时，加速度计安装误差角个数可从6项降为3项。

1.3 系统模型

由于系统观测量选取不同以及平台坐标系定义不同，惯性平台连续翻滚自标定存在不同系统模型，其中系统动力学模型有失准角、框架角和姿态角等模型，观测模型有框架角、加速度计等模型。

为了简化分析，假设惯性仪表自身误差已由多位置等标定方案标定并已予补偿。

1.3.1 系统运动学方程

惯性平台失准角运动学方程[5]可写为：

(11)

平台框架角运动学方程[11]为：

(12)

考虑到平台基座安装误差角，基座角速度可表示为：

(13)

若式(12)中α，β和γ为平台坐标系姿态角，则式(12)可以改写为：

(14)

1.3.2 系统观测方程

惯性平台自标定中，采用的观测量有平台框架角和加速度计输出等。其中框架角观测方程可写为：

(15)

不考虑加速度计自身误差时，加速度计输出可写为：

(16)

由上述系统方程和观测方程可构建不同的系统模型。

1)系统模型一。选择平台失准角运动方程和加速度计输出方程作为系统模型，即：

(17)

为了反映观测量与平台失准角之间联系，可采用加速度计输出误差为观测量，即：

(18)

(19)

故系统模型一可表示为：

(20)

2)系统模型二。选择平台框架角运动方程和框架角观测方程以及加速度计输出方程作为系统模型，即：

(21)

3)系统模型三。选择平台框架角运动方程和加速度计输出方程作为系统模型，即：

(22)

4)系统模型四

选择平台姿态角运动方程和加速度计输出方程作为系统模型，即：

(23)

综上所述，在惯性平台自标定中，根据不同的系统动力学模型和观测模型共可构建四种系统模型，而每种模型中惯性仪表安装误差矩阵形式与惯性平台坐标系的定义息息相关。

2 惯性仪表安装误差可观测性分析

针对上述四种模型在不同平台坐标系定义下惯性仪表安装误差的可观测性展开分析。

2.1 模型一可观测性分析

2.1.1 pa系为平台坐标系

(24)

由式(24)易知，模型一属于线性时变系统，其中单个时间段内系统可观测性矩阵Qj为：

(25)

当ωc存在多个非共线值时，即可保证系统满秩。根据PWCS理论[12]，模型一在pa系定义下，系统是完全可观的。

2.1.2 ps系为平台坐标系

(26)

考虑到式(10)，式(26)可改写为：

(27)

(28)

式(28)表明，模型一在ps系的定义下，无法区分平台失准角ψ与加速度计部分安装误差角θaC。而θaC的错误估计会影响θgC以及ψ的估计，因此系统中ψ，θgC和θaC不可观，仅θaT和θgT可观。

综上所述，当系统采用平台失准角模型和加速度计输出构建系统模型时，平台坐标系必须以pa系为定义，否则系统不完全可观。

2.2 模型二可观测性分析

根据惯性平台工作原理，平台指令角速度信号由陀螺仪传递至平台各框架轴的力矩电机，驱动平台按照指令旋转。实际上，陀螺仪与平台框架均以平台六面体为基准进行安装，故平台框架角运动学方程中平台坐标系必须以平台六面体为基准进行定义，即模型为：

(29)

假设ωc远大于地球自转角速度ωie，当θA已知时，有：

(30)

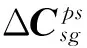
(31)

综上所述，当系统模型以框架角运动学方程和框架角以及加速度计输出观测方程建模时，必须以平台六面体为基准定义平台坐标系，此时加速度计6项安装误差、陀螺仪6项安装误差和2项平台基座安装误差可观，1项平台基座安装误差不可观。

2.3 模型三可观测性分析

2.3.1 pa系为平台坐标系

(32)

(33)

(34)

两边同时对时间求导并化简，有：

(35)

由系统运动学方程(32)得：

(36)

(37)

将式(37)和式(34)代入式(35)，有：

(38)

当ωc为恒值时，有：

(39)

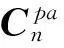
综上所述，模型三中仪表安装误差可观，而基座安装误差角不可观。

2.3.2 ps系为平台坐标系

(40)

式(40)可改写为：

(41)

假设平台上存在两个六面体，由其确定的平台坐标系为ps1和ps2两个坐标系，系统模型(41)在上述两个坐标系下可分别写为：

(42)

和

(43)

因为六面体与平台固连，故：

2.4 模型四可观测性分析

2.4.1 pa系为平台坐标系

(44)

由于系统模型中利用姿态角代替框架角构建系统动力学模型，故模型中不包含基座安装误差。由2.3节中的结论可知，此时系统完全可观。

2.4.2 ps系为平台坐标系

(45)

由2.3节中的结论，系统模型四在六面体定义下不可观。

综上所述，当系统模型以姿态角模型和加速度计输出模型建立时，为保证系统完全可观，平台坐标系必须以pa系定义，此时，系统不包含基座安装误差，加速度计3项安装误差和陀螺仪6项安装误差完全可观。

3 仿真

3.1 仿真参数

将惯性仪表安装误差设置为：

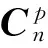
(46)

平台连续翻滚路径与文献[5]一致，即初始对准导航系，平台按照绕南旋转180°，绕东旋转90°，绕南旋转180°，绕东旋转90°顺序转动，其中转速为0.1°/s；测量噪声为1×10-6g；陀螺仪测量噪声为0.1°/h；框架角测量噪声为10″。

滤波器初值为0，滤波周期为1s，其余参数根据系统进行设置，采用4阶龙格库塔积分算法。

3.2 仿真结果

图1～28为加速度计和陀螺仪安装误差角在不同模型不同平台坐标系定义下的仿真结果，其中所有图中y轴单位为°。

3.2.1 模型一仿真结果

图1～3为模型一以pa系定义平台坐标系时滤波结果示意图。从图中可以看出，加速度计3项安装误差、陀螺仪6项安装误差滤波曲线收敛较好，估计误差较小，系统完全可观。

图4～7为模型一以ps系为平台坐标系时滤波结果示意图。从图中可以看出，θgC和θaC滤波曲线收敛至错误值，θaT和θgT滤波曲线收敛较好，估计误差较小，因此θgC和θaC不可观，θaT和θgT可观，该结论与理论分析结果一致。

综上所述，当采用失准角和加速度计输出构建系统模型时，必须以加速度计敏感轴坐标系定义平台坐标系，否则系统不可观。

3.2.2 模型二仿真结果

图8～12为模型二在ps系为平台坐标系定义方式下的仿真结果图。从图中可以看出加速度计6项安装误差和陀螺仪6项安装误差角估计效果较好，收敛精度高。对于基座安装误差λ，由于λy没有激励，其估值一直为零。因此，除了λy以外，系统各项误差系数滤波效果较好。仿真结果与2.2节理论分析结果一致。

3.2.3 模型三仿真结果

图13～16为模型三在pa系为平台坐标系定义方式下仿真结果图。从图中可以看出，仪表安装误差滤波效果较好，均可观。但基座安装误差滤波曲线收敛至错误值，即不可观。图17～21为模型三在ps系为平台坐标系定义方式下的仿真结果图。从图中可以看出，除部分误差系数收敛至真值以外，大多数误差系数收敛至错误值甚至不收敛，即系统不可观。

图1 模型一在pa系下滤波曲线Fig.1 Flitting curve of with model 1 and pa coordinate frame

图2 模型一在pa系下θgT滤波曲线Fig.2 Flitting curve of θgT with model 1 and pa coordinate frame

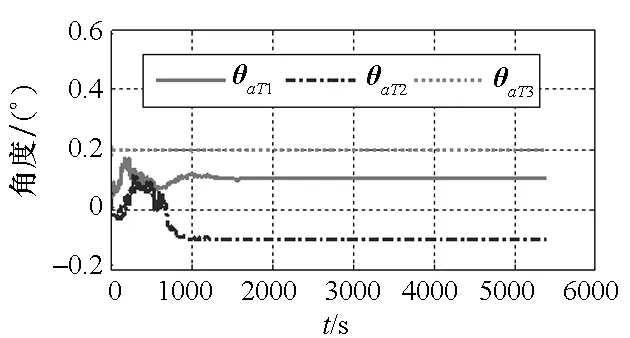
图3 模型一在pa系下θaT滤波曲线Fig.3 Flitting curve of θaT with model 1 and pa coordinate frame

图4 模型一在ps系下θgC滤波曲线Fig.4 Flitting curve of θgC with model 1 and ps coordinate frame

图5 模型一在ps系下θgT滤波曲线Fig.5 Flitting curve of θgT with model 1 and ps coordinate frame

图6 模型一在ps系下θaC滤波曲线Fig.6 Flitting curve of θaC with model 1 and ps coordinate frame

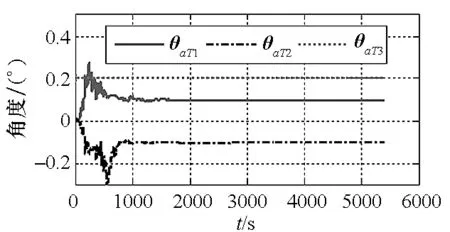
图7 模型一在ps系下θaT滤波曲线Fig.7 Flitting curve of θaT with model 1 and ps coordinate frame

图8 模型二在ps系下θgC滤波曲线Fig.8 Flitting curve of θgC with model 2 and ps coordinate frame

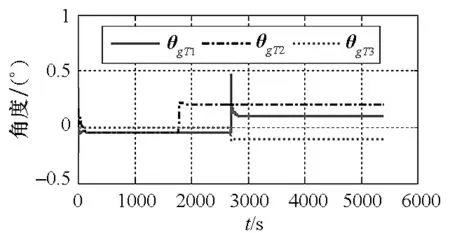
图9 模型二在ps系下θgT滤波曲线Fig.9 Flitting curve of θgT with model 2 and ps coordinate frame

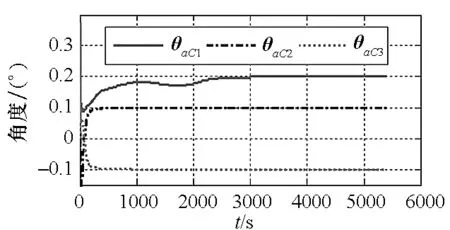
图10 模型二在ps系下θaC滤波曲线Fig.10 Flitting curve of θaC with model 2 and ps coordinate frame

图11 模型二在ps系下θaT滤波曲线Fig.11 Flitting curve of θaT with model 2 and ps coordinate frame

图12 模型二在ps系下λ滤波曲线Fig.12 Flitting curve of λ with model 2 and ps coordinate frame

图13 模型三在pa系下滤波曲线Fig.13 Flitting curve of with model 3 and pa coordinate frame

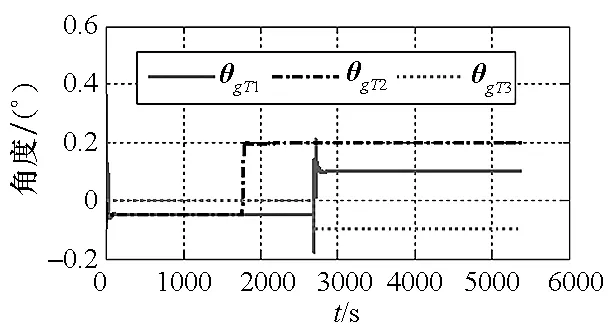
图14 模型三在pa系下θgT滤波曲线Fig.14 Flitting curve of θgT with model 3 and pa coordinate frame

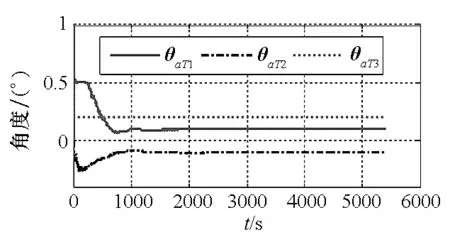
图15 模型三在pa系下θaT滤波曲线Fig.15 Flitting curve of θaT with model 3 and pa coordinate frame

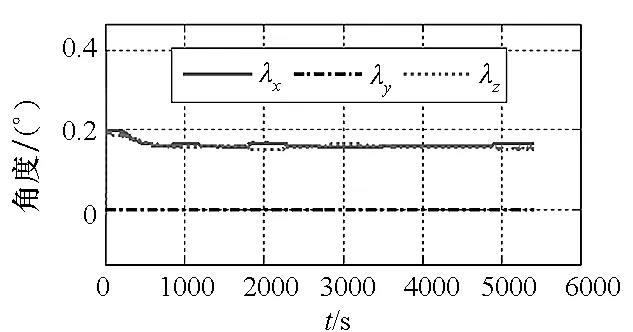
图16 模型三在pa系下λ滤波曲线Fig.16 Flitting curve of λ with model 3 and pa coordinate frame

图17 模型三在ps系下θgC滤波曲线Fig.17 Flitting curve of θgC with model 3 and ps coordinate frame

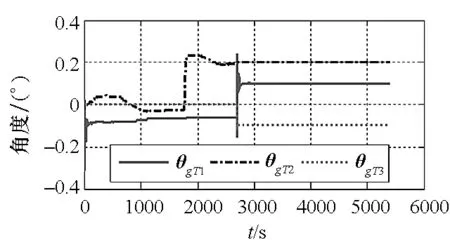
图18 模型三在ps系下θgT滤波曲线Fig.18 Flitting curve of θgT with model 3 and ps coordinate frame

图19 模型三在ps系下θaC滤波曲线Fig.19 Flitting curve of θaC with model 3 and ps coordinate frame

图20 模型三在ps系下θaT滤波曲线Fig.20 Flitting curve of θaT with model 3 and ps coordinate frame

图21 模型三在ps系下λ滤波曲线Fig.21 Flitting curve of λ with model 3 and ps coordinate frame

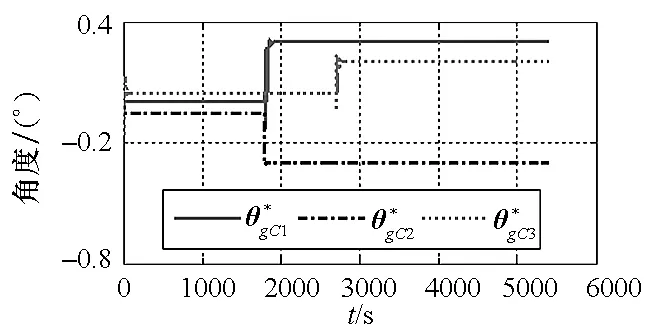
图22 模型四在pa系下滤波曲线Fig.22 Flitting curve of with model 4 and pa coordinate frame

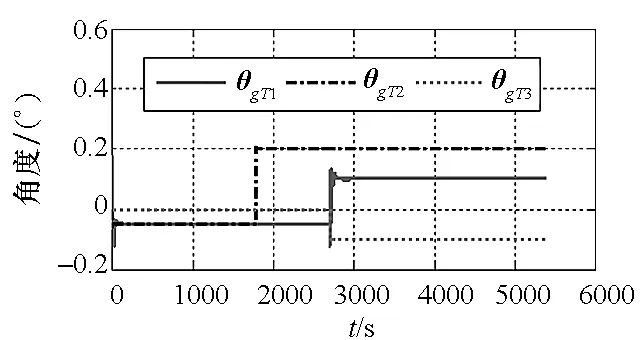
图23 模型四在pa系下θgC滤波曲线Fig.23 Flitting curve of θgC with model 4 and pa coordinate frame

图24 模型四在pa系下θgC滤波曲线Fig.24 Flitting curve of θgC with model 4 and pa coordinate frame

图25 模型四在ps系下θgC滤波曲线Fig.25 Flitting curve of θgC with model 4 and ps coordinate frame

图26 模型四在ps系下θgT滤波曲线Fig.26 Flitting curve of θgT with model 4 and ps coordinate frame

图27 模型四在ps系下θaC滤波曲线Fig.27 Flitting curve of θaC with model 4 and ps coordinate frame

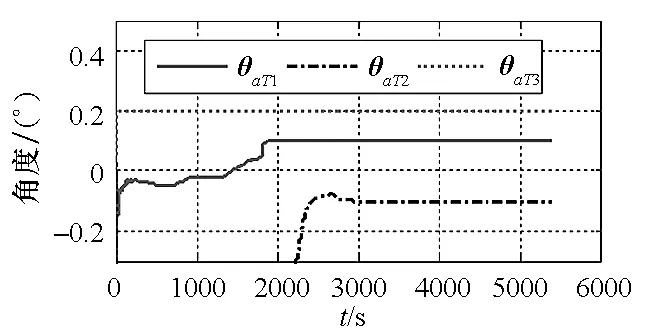
图28 模型四在ps系下θaT滤波曲线Fig.28 Flitting curve of θaT with model 4 and ps coordinate frame

上述仿真结果验证了2.3节中理论分析结果。

4)模型四仿真结果

图22～24为模型四在pa系为平台坐标系定义方式下的仿真结果图。从图中可以看出，各项惯性仪表安装误差滤波曲线收敛较快，收敛精度高，此时系统完全可观。

图25～28为模型四在ps系为平台坐标系定义方式下的仿真结果图。从图中可以看出，除部分误差系数收敛至真值以外，大多数误差系数收敛至错误值甚至不收敛，此时系统不可观。

上述仿真结果与前一节中理论分析结果一致，充分验证了理论分析结果的正确性，也直观地反映了系统模型和平台坐标系定义方式对惯性仪表安装误差可观测性的影响。

4 结论

针对惯性平台自标定中惯性仪表安装误差可观测性问题，研究了系统模型、平台坐标系定义方式和惯性仪表安装误差可观测性之间的关系。通过理论推导与分析，可以得到以下结论：

1)当观测量仅为加速度计输出时，为保证系统完全可观，系统动力学模型可选择失准角模型或姿态角模型，但平台坐标系以pa系为其定义，此时系统包含加速度计3项安装误差，陀螺仪6项安装误差，不需考虑基座安装误差。

2)当观测模型中包含平台框架角时，系统动力学模型必须选择框架角模型，平台坐标系必须按照ps系定义。此时，系统模型中包含加速度计6项安装误差、陀螺仪6项安装误差和3项基座安装误差。各仪表安装误差可观，但仅有2项基座安装误差角可观。

上述结论为惯性平台连续翻滚自标定方案中系统模型的建立和平台坐标系的选择提供了理论支撑，并可用于后续平台旋转路径设计中，具有重要意义。

References)

[1] 包为民， 申功勋， 李华滨. 惯性平台在系统中多位置翻滚自标定方法[J]. 北京航空航天大学学报, 2011, 37(4): 462-465.

BAO Weimin, SHEN Gongxun, LI Huabin.Investigation on inertial platform multi-position rolling self-calibration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(4): 462-465. (in Chinese)

[2] 杨华波, 蔡洪, 张士峰. 高精度惯性平台误差自标定方法[J]. 上海航天, 2006, 23(2): 33-36.

YANG Huabo, CAI Hong, ZHANG Shifeng.Calibration for the errors of a high accurate inertial platform [J]. Aerospace Shanghai, 2006, 23(2): 33-36. (in Chinese)

[3] 唐江河, 付振宪, 邓正隆. 基于灵敏度分析的惯导平台参数分步辨识方法[J]. 宇航学报, 2008, 29(6): 1845-1851.

TANG Jianghe, FU Zhenxian, DENG Zhenglong. The sub-step identification of inertial platform drift error coefficients based on sensitivity analysis [J]. Journal of Astronautics, 2008, 29(6): 1845-1851. (in Chinese)

[4] 付振宪, 邓正隆. 灵敏度分析在惯导平台误差参数辨识中的应用[J]. 系统工程与电子技术, 2001, 23(7): 55-57. FU Zhenxian, DENG Zhenglong. Application of sensitivity analysis in inertial platform error parameters identification [J]. Systems Engineering and Electronics, 2001, 23(7): 55-57. (in Chinese)

[5] Andrew D J. Continuous calibration and alignment techniques for an all-attitude inertial platform [C]//Proceedings of AIAA Guidance and Control Conference, 1973: 20-22.

[6] Fitzgerald W J, Shapanka M J. An azimuth verification technique for an advanced inertial reference sphere[C]//Proceedings of Eighth Guidance and Control Conference, 1977.

[7] 杨华波, 蔡洪, 张士峰, 等. 高精度惯性平台连续自标定自对准技术[J]. 宇航学报, 2006, 27(4): 600-604.

YANG Huabo, CAI Hong, ZHANG Shifeng, et al. Continuous calibration and alignment techniques for a high precision inertial platform [J]. Journal of Astronautics, 2006, 27(4): 600-604. (in Chinese)

[8] 曹渊, 张士峰, 杨华波, 等. 惯导平台误差快速自标定方法研究[J]. 宇航学报, 2011, 32(6): 1281-1287.

CAO Yuan, ZHANG Shifeng, YANG Huabo, et al. Research on rapid self-calibration method for inertial platform [J]. Journal of Astronautics, 2011, 32(6): 1281-1287. (in Chinese)

[9] 曹渊, 张士峰, 杨华波, 等. 一种新的惯性平台快速连续旋转自对准方法[J]. 兵工学报, 2011, 32(12): 1468-1473.

CAO Yuan, ZHANG Shifeng, YANG Huabo, et al.Fast self-alignment method for inertial platform through continuous rotation [J]. Acta Armamentarii, 2011, 32(12): 1468-1473. (in Chinese)

[10] Cao Y, Cai H, Zhang S F, et al. A new continuous self-calibration scheme for a gimbaled inertial measurement unit [J]. Measurement science and technology, 2012, 23(1): 385-394.

[11] Hellings F J. Application of extended Kalman filtering to a dynamic laboratory calibration of an inertial navigation system[R]. AD 763718: 77-118.

[12] Goshen-Meskin D, Bar-Itzhack I Y. Observability analysis of piece-wise constant systems-part I: theory [J]. IEEE Transaction on Aerospace and Electronic Systems, 1992, 28(4): 1056-1067.

[13] Ding Z J, Cai H, Yu C M, et al.Novel low cost calibration methods for MEMS inertial/magnetic integrated sensors[C]//Proceedings of IEEE Chinese Guidance, Navigation and Control Conference, 2014: 505-511.

[14] Wu Y X, Zhang H L, Wu M P, et al.Observability of strapdown INS alignment: a global perspective [J]. IEEE Transation on aerospace and electronic systems, 2012, 48(1): 78-102.

Observability analysis for misalignments of inertial sensors in inertial platform self-calibration

DING Zhijian, CAI Hong, ZHANG Wenjie

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

For the observability of inertial sensor misalignments in inertial platform self-calibration problem, the effects of the system model and platform coordinate frame on observability were analyzed. Based on different system dynamic models and measurement vectors, four system models were built. The observability of inertial sensors misalignments in different models with different definitions of platform coordinate frame was investigated. The theory conclusions and simulation results show that the system is observable only in two conditions: the system measurement models are built up with platform angles and accelerometer triad outputs, the system dynamic model is built up with platform angles and the platform coordinate frame should be defined with the benchmark hexahedron of platform; the system measurement models are built up only with accelerometers triad outputs, the system dynamic models are built up with platform attitude or misalignment models and the platform coordinate frame should be defined with the accelerometer sensor axes.

observability; misalignment; self-calibration; inertial platform

10.11887/j.cn.201605020

http://journal.nudt.edu.cn

2015-05-18

航天科技创新基金资助项目(CASC201105)

丁智坚(1988—)，男，新疆乌鲁木齐人，博士研究生，E-mail：dzjqe@126.com；蔡洪(通信作者)，男，教授，博士，博士生导师，E-mail：hcai@nudt.edu.com

V448. 12

A

1001-2486(2016)05-127-10