火星稀薄大气动态误差对制动降轨的影响*

方宝东，吴美平，张 伟

(1.国防科技大学 机电工程与自动化学院， 湖南 长沙 410073； 2.上海卫星工程研究所， 上海 200240；3.上海市深空探测技术重点实验室， 上海 200240)



火星稀薄大气动态误差对制动降轨的影响*

方宝东1,2,3，吴美平1，张 伟2,3

(1.国防科技大学 机电工程与自动化学院， 湖南 长沙 410073； 2.上海卫星工程研究所， 上海 200240；3.上海市深空探测技术重点实验室， 上海 200240)

针对火星大气制动降轨过程中稀薄流区大气受季节和昼夜等因素影响而存在较大动态误差的问题，建立气动力作用下的轨道动力学方程，研究探测器稀薄流气动参数计算方法，分析大气参数动态误差对气动力及制动降轨效果的影响。结合火星探测应用，仿真分析火星大气制动过程中的探测器气动特性以及轨道变化特性。为保证探测器制动过程中的安全和持续时间要求，给出了理想的大气制动降轨走廊范围及导航精度需求，具有一定的工程参考价值。

火星探测；大气模型；大气制动；动态误差

火星探测是当前国内外深空探测的热点之一。对于火星探测任务，大速度增量需求导致的发射质量及携带燃料的局限是制约任务的重要因素。大气制动降轨方法是使探测器既节省推进燃料又快速准确地到达目标轨道的有效手段。这一技术能最大限度地降低所需燃料的质量，探测器也能承载更多的有效载荷，完成更多的科学探测任务；在有效载荷质量不变的情况下减轻探测器总质量，降低对火箭运载能力的要求，节省发射成本。

目前，在深空探测任务中已成功实施4次大气制动降轨[1-3]，具体参数见表1。

表1 大气制动降轨技术典型应用

可见，大气制动技术在行星探测任务中发挥着重要的作用，该技术目前仅美国成功应用[4-6]，在我国刚刚起步，暂无工程实际应用，值得深入研究。

在大气制动过程中，探测器在近火点处于火星高层大气稀薄流区，探测器需要保持稳定的姿态，并经受与火星高层大气摩擦产生的过载和气动热。制动的高度与任务时间和任务安全性密切相关：太高则任务时间太长，影响科学探测任务的执行；太低则存在坠毁的风险[7-10]。火星高层大气易受季节和昼夜变化影响，大气密度、温度等参数动态误差变化大[11-13]。本文从探测器本体和太阳帆板能够承受的过载和热流以及探测任务执行时间等实际工程约束条件出发，研究火星大气动态误差对制动降轨的影响，确定合适的制动走廊范围，进而提出对探测器导航定轨的精度要求。

1 大气制动降轨基本原理

火星大气制动降轨方法利用火星上层大气的阻力作用来改变探测器的速度，从而使探测器达到预定轨道[14-16]。探测器进入环火大椭圆轨道后，通过改变近火点的高度，使轨道近火点处于火星上层大气中。当探测器经过近火点附近时利用大气与探测器的摩擦阻力来减缓运行速度，从而降低远火点的高度。通过一系列这样的制动过程后，再将近火点高度提高到火星大气层外，最终实现探测器减速至预定轨道运行，整个大气制动过程如图1所示。

图1 火星大气制动降轨原理图Fig.1 Schematic diagram of aerobraking in Mars

大气制动降轨初期，由于近火点速度较大，气动阻力较大，可使远火点高度降低得较快；大气制动末期，随着远火点高度的降低，近火点速度减小，气动阻力减小，远火点高度降低变慢，直至降低至要求高度。

2 数学建模

2.1 动力学方程

探测器在大气层外时，在火星惯性坐标系下描述探测器的运动状态。当轨道高度低于125 km时，大气密度大于2×10-8kg/m3，气动力大于引力的1/105，认为探测器进入火星大气。探测器进入火星大气后，在火星固连坐标系下描述探测器的运动状态。气动力和力矩的计算是在探测器本体坐标系下进行的，应用时需要转换到火星固连坐标系下[17-19]。

在大气层内，火星固连坐标系下轨道动力学方程为：

(1)

(2)

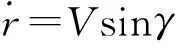
(3)

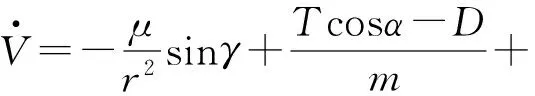
Ω2rcosλ(sinγcosλ-cosγsinχsinλ)

(5)

(6)

其中：δ为经度，λ为纬度，r为探测器到火心的距离，V为探测器的速度，γ为轨迹倾角，χ为航向角，T为推力，D为气动阻力，L为气动升力，Ω为火星自转角速度，α为攻角，σ为滚转角，m为探测器质量。

在大气层外，惯性系下探测器的运动可描述为：

(7)

(8)

(9)

(10)

(11)

(12)

其中：δ*为赤经，λ*为赤纬，r*为探测器到火心的距离，V*为探测器的速度，γ*为轨迹倾角，χ*为航向角，T为推力。

2.2 气动参数计算

火星大气制动处于火星高层大气，气动参数计算需考虑稀薄气体效应，一般的气体动力学理论都是以连续介质假设为前提的，当流动中分子的平均自由程与物体特征尺度相当时，气体分子间断效应就会显现出来，连续介质假设不再成立[20-22]。因此，针对火星大气制动气动参数计算问题，需要研究稀薄气体条件下气动参数的计算方法。

设来流分子数密度为n∞，来流温度为T∞，分子速度分量为Vx，Vy，Vz，来流速度为V∞。入射分子的速度分布函数为：

(13)

其中，k是Boltzmann常数，u′，v′，w′是分子热运动速度的3个分量。

(14)

根据分布函数，通过计算入射分子(Vx>0的为入射分子)带来动量和反射分子(Vx<0的为反射分子)带走的动量的统计平均值就可以得到物体表面的压力和剪切应力。

(15)

(16)

其中：Q，R，N的表达式分别为：

(17)

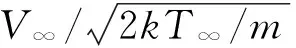
从式(15)～(17)可以看到，决定物体表面的压力p和剪切力τ的参数有：来流条件ρ∞，V∞，T∞，壁面温度和来流温度比Tw/T∞，来流和物面的夹角θ，物体表面动量适应系数σ′，σ，分子质量m。

有了壁面压力和剪切应力的表达式，就可以根据给定的物体表面几何形状，积分得到作用于物体上的轴向力、法向力和俯仰力矩，从而得到轴向力系数CA、法向力系数CN和偏航力矩系数Cmz。

根数气动力系数可以得到轴向和法向气动力的大小为：

(18)

(19)

阻力D、升力L和轴向力A、法向力N之间的转换关系为：

D=Acosα+Nsinα

(20)

L=-Asinα+Ncosα

(21)

2.3 大气模型

火星大气按照成分、温度、气体同位素特征以及大气气体的物理性质，一般分为上、中、下三层。200 km以上为上层大气，45～200 km为中层大气，45 km以下为下层大气[23-25]。

火星的大气密度不仅与高度有关，而且具有明显的季节性变化特点[26-28]。由于火星大气参数动态误差的存在使得不同探测任务测量到的火星大气参数差异较大，如图2所示。

图2 MGS，MRO，ODY测量的大气密度Fig.2 Atmosphere density measured by MGS/MRO/ODY

火星大气模型有指数模型、大气平均变化性质模型、Mars-GRAM大气模型等[29-31]。以Mars-GRAM大气模型为例，其温度、声速、压强、密度随高度变化的曲线如图3所示。

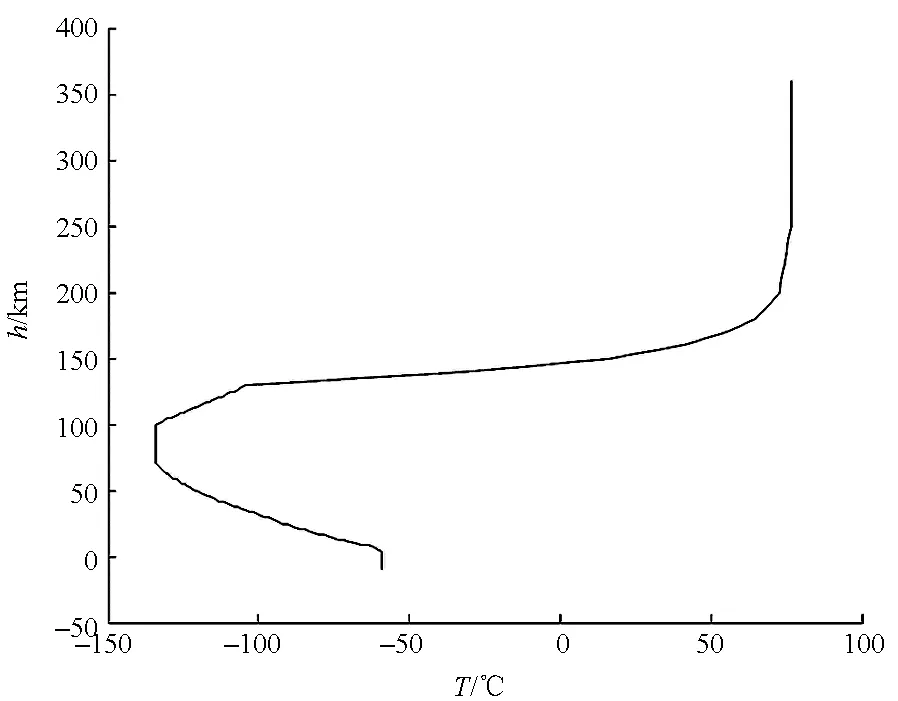
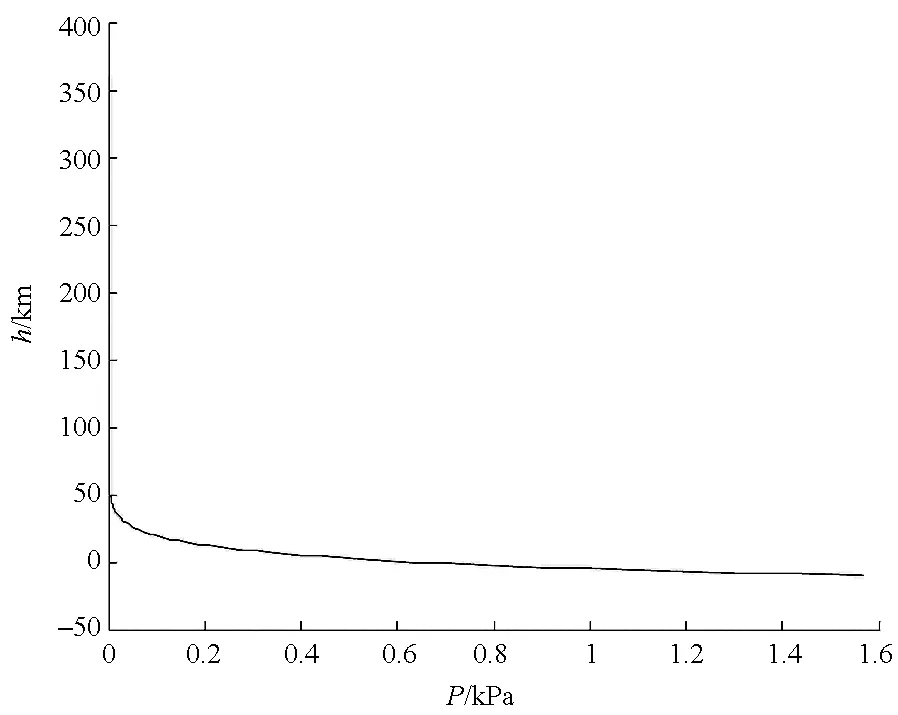
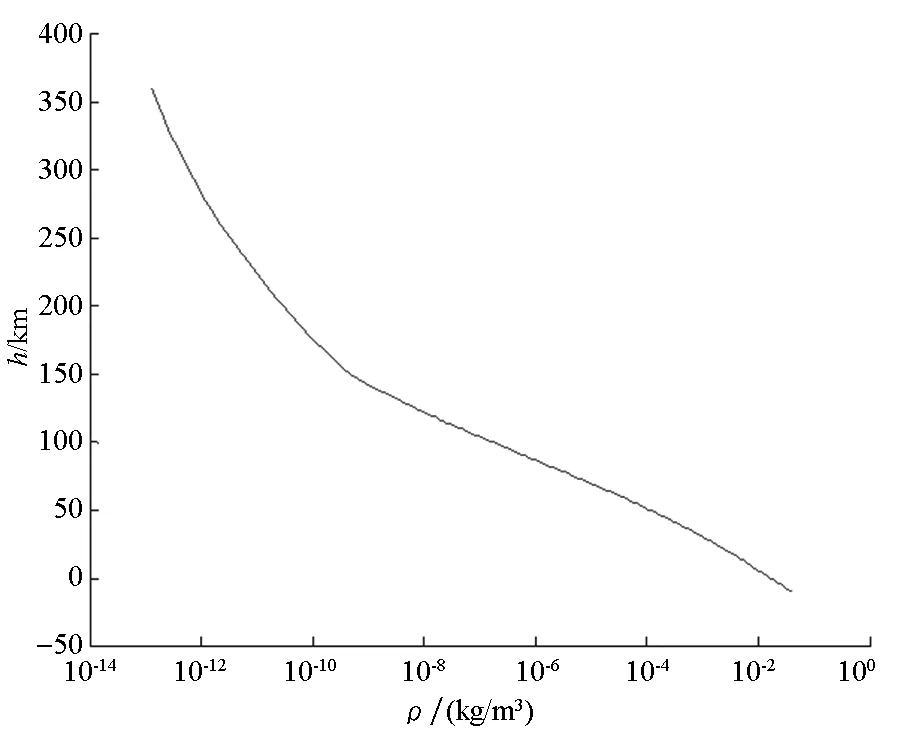
图3 Mars-GRAM大气模型参数变化曲线Fig.3 Curve of Mars-GRAM parameters

不同的大气密度模型建模的机理不同，其数值也迥异，如表2所示为三种大气模型参数对比。

大气平均变化性质模型的有效使用范围通常在30 km以下，其计算所得的大气密度数据与Mars-GRAM提供的数据在30 km以下符合得较好。指数大气模型在50 km以上时与Mars-GRAM模型差距较大，在高度达到125 km时，其比值达到5 ∶1。

表2 不同大气模型数据对比

因此，在火星大气制动降轨任务中，采用任何一种大气模型都不能准确表示火星大气密度状态，必须考虑火星稀薄大气动态误差的影响。

3 仿真分析

为了分析大气参数误差对制动降轨的影响，本节在给出基本设计约束条件后，对大气制动近火点高度进行了选取，对大气参数误差对轨道的影响进行了计算。

3.1 基本设计约束

面向应用需求，对火星探测器实际模型进行简化处理，图4给出了大气制动期间探测器简化模型图，其中太阳帆板是主要的制动面(即迎风面)。

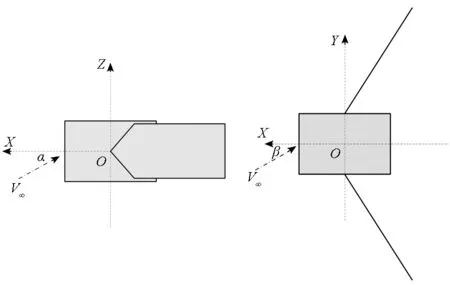
图4 大气制动过程制动面与来流夹角Fig.4 Angle between brake surface and incoming flow during aerobraking

本算例采用了如下计算条件：火星探测器制动捕获后进入近火点高度为110 km，远火点高度为80 000 km的环火大椭圆轨道；太阳帆板面积为12 m2，与Y轴方向的夹角为30°；火星大气来流速度取4800 m/s；流动特征长度取7.3 m；流场计算区域为X方向(-10 m，10 m)，Y方向(-20 m，20 m)，Z方向(-3 m，3 m)。火星大气模型以Mars-GRAM2005给出的高度间隔1 km大气模型参数进行插值计算得出，插值方法采用分段三次Hermite插值。

来流气体温度、密度、压强及其对应的努森数、雷诺数见表3。

表3 火星大气高度-密度-努森数对应表

3.2 大气制动近火点高度分析

获取合适的大气阻力是进行大气制动降轨的关键环节。大气制动降轨过程中，若气动力偏小就无法达到快速减小环火轨道半长轴的目的；若气动偏大，可能会导致探测器的关键结构被破坏。

大气制动过程中，设计确定合适的气动力需要综合考虑多方面要素，包括了近火点处飞行速度、近火点高度、探测器构型等。因此，精确地对探测器在大气制动过程中所遇到的气动力状态进行模拟计算是非常重要的。

为了分析大气制动模型的稀薄气体动力学特性，根据轨道特点计算探测器的阻力系数变化情况如图5所示，气动阻力系数随大气密度的增加而降低。偏航力矩系数变化如图6所示，偏航力矩系数的符号与侧滑角相反，故探测器在制动过程中为姿态稳定状态。

图5 阻力系数随来流密度的变化曲线Fig.5 Relation between drag coefficient and coming flow density

图6 偏航力矩系数变化曲线Fig.6 Variational curve of yaw moment coefficient

动压和气动阻力的变化曲线如图7、图8所示，动压随高度的降低呈指数形式地增加，阻力的变化与其是一致的。

图7 动压随高度的变化曲线Fig.7 Relation between dynamic pressure and altitude

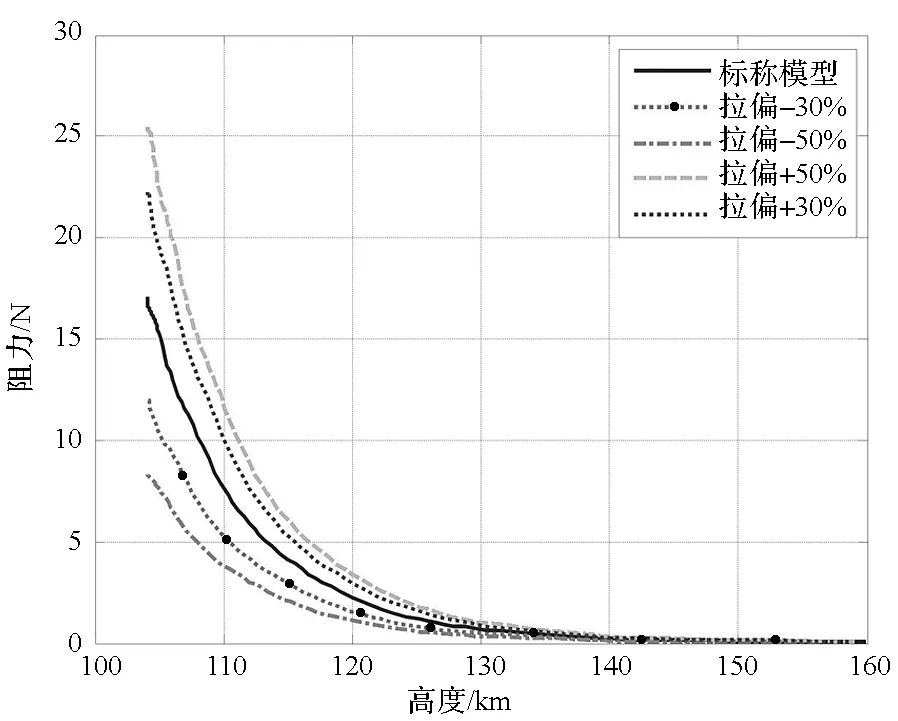
图8 阻力随高度的变化曲线Fig.8 Relation between drag force and altitude

在实际的大气制动过程中，为了获取合适的大气阻力进行大气制动，而又不至于破坏探测器的关键结构，需要根据实际的飞行状况和探测器的材料特性来给定一个制动范围，即将探测器表面的热流密度和表面压力的上下极限值控制在一定的区域内。若低于这个高度，探测器所承受的最大压力将超过预定边界，有可能对探测器的结构造成破坏，必须避免。由仿真结果可以得出两个结论：一是近火点附近动压随高度的变化敏感，以标称模型曲线为例，在高度100 km附近，高度每变化1 km，动压变化20%左右；二是大气模型偏差对动压的影响很大，若大气模型有±50%的偏差，则对应的动压最大值将是最小值的3倍。因此，大气制动的近火点偏差对探测器的过载和热流影响很大，需要精确控制大气制动时近火点的高度。结合工程经验，取大气制动近火点高度为110 km。

3.3 大气参数误差对轨道的影响

根据探测器大气制动过程中受力分析可知，探测器在大气制动过程中，主要受火星引力和气动阻力作用。依据轨道动力学方程可以计算出探测器的速度变化△V、高度变化△H，继而获得整个大气制动过程中轨道的变化情况。

在大气制动过程中，通过轨道仿真可根据探测器能允许的制动区域及制动需求来调整探测器的姿态以获取最优的轨道变化量，并最终达到最优的大气制动轨道。大气制动轨道仿真框图如图9所示。

图9 大气制动轨道仿真框图Fig.9 Aerobraking orbit simulation block diagram

根据上节的基本设计参数，目标轨道选取1000 km×1500 km的环火轨道，大气制动降轨期间探测器姿态维持在零攻角附近，其仿真结果如图10所示。

图10 大气制动过程仿真结果Fig.10 Aerobraking process simulation result

图11 大气制动过程轨道半长轴变化情况Fig.11 Semimajor axis variation during aerobraking

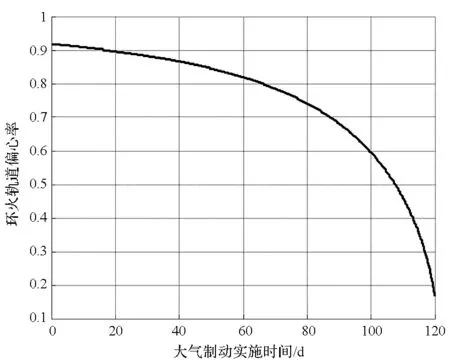
图12 大气制动过程轨道偏心率变化情况Fig.12 Eccentricity variation during aerobraking process

从图11、图12可见，采用大气制动降轨方法使环火轨道远火点高度从80 000 km降低至1500 km将耗时约120 d。整个过程中探测器的轨道远火点的高度不断降低，制动效果明显。大气制动过程使探测器近火点速度减小了1060 m/s，可节约440 kg燃料。

在大气制动初期，探测器在近火点处速度较大，每轨大气制动产生的速度增量较大，半长轴衰减明显。当大气制动末期，每轨大气制动产生的速度增量逐渐减小。整个过程中轨道周期同时持续减小，因此半长轴衰减近似呈线性趋势。

考虑到目前火星大气模型存在较大的误差，且由于季节变化，大气模型参数存在周期性波动，为保证工程应用过程中的可靠性，对大气模型进行±30%，±50%的拉偏进行对比仿真，如图13所示。

图13 大气参数拉偏后的制动效果Fig.13 Aerobraking effect deviating from nominal model

结果显示，当大气模型存在30%以上的偏差时，远火点可能降低至安全高度以下，存在撞击火星的危险。特别是在大气制动末期，由于轨道周期的减小，环火轨道远火点高度呈加速衰减趋势，每天的衰减速率大致为500 km。

火星大气密度随高度变化，且呈近似指数变化的特点，轨道高度越低密度变化越显著。因此在近火点处高度的差异对制动降轨的影响巨大。如图14所示，若近火点高度大于115 km，完成上述的大气制动降轨任务将耗时223 d。这对于实际的工程任务而言，往往是难以接受的。而另一方面，近火点高度的下降将导致气动力呈指数增大。在制动末期，若轨道近火点高度低于105 km，大气密度偏差大于30%，将导致每天远火点高度额外衰减500 km以上，存在坠入火星大气的危险。

面向深空探测任务中的应用需求，考虑火星大气模型存在30%偏差，综合探测器对气动力的承受能力及大气制动降轨过程持续时间等约束，大气制动降轨轨道近火点选取为110 km±5 km是较为理想的大气制动降轨走廊范围。在目标轨道高度在1000 km附近的火星大气制动降轨任务中，根据所选取的标称走廊范围，探测器在近火点高度110 km实施大气制动降轨需要具备导航精度优于5 km的导航能力，以保证探测器能及时抬高近火点轨道高度，确保安全进入工作轨道。

图14 不同近火点高度的制动降轨时间Fig.14 Aerobraking durations of different perigee altitudes

4 结论

火星大气受季节、昼夜等因素复杂多变，大气模型参数存在较大的动态误差，是在火星大气制动降轨任务中必须考虑的因素。通过对大气制动过程轨道动力学方程、气动力计算方程及火星大气模型的建模与仿真，研究了火星大气制动降轨过程中火星大气动态误差对制动降轨动压、阻力和时间的影响。仿真结果表明，大气参数动态误差对制动降轨影响巨大，甚至导致探测器存在撞击火星的危险。综合探测器对气动力的承受能力及大气制动降轨过程持续时间等约束，轨道近火点选取为110 km±5 km是理想的大气制动降轨走廊范围。本文的研究结果具有一定的工程应用价值。在下一步的研究过程中将综合考虑姿态控制误差、气动力气动热的耦合作用等因素的影响。

References)

[1] Takashima N, Wilmoth R. Aerodynamics of Mars odyssey[C]// Proceedings of AIAA Atmospheric Flight Mechanics Conference and Exhibit, AIAA 2002-0809, 2002.

[2] Jah M K, Lisano M E, Born G H, et al. Mars aerobraking spacecraft state estimation by processing inertial measurement unit data[J]. Journal of Guidance Control & Dynamics, 2015, 31(6): 1802-1812.

[3] Prince J L H, Chavis Z Q, Wilmoth R G. Modeling reaction-control system effects on Mars odyssey[J]. Journal of Spacecraft and Rockets, 2005, 42(3): 444-449.

[4] Justus C G. Mars global reference atmospheric model for mission planning and analysis[J]. Journal of Spacecraft & Rockets, 1991, 28(2): 216-221.

[5] Johnson W, Longuski J, Lyons D.High-fidelity modeling of semi-autonomous attitude control during aerobraking [C]//Proceedings of AIAA/AAS Astrodynamics Specialist Conference and Exhibit, AIAA 2002-4909, 2002.

[6] Finchenko V, Ivankov A,Shmatov S. Aerobraking and aerocapture:aerodynamic and aerothermal study, applicability of inflatable structures[C]//Proceedings of 16th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2001-2057, 2001.

[7] Hanna J, Tolson R, Cianciolo A D, et al.Autonomous aerobraking at Mars[C]//Proceedings of 5th International ESA Conference on Guidance Navigation and Control Systems and Actuator and Sensor Product Exhibition, 2002.

[8] Hall J L, Noca M A, Bailey R W.Cost-benefit analysis of the aerocapture mission set [J].Journal of Spacecraft and Rockets, 2005, 42(2): 309-320.

[9] Tolson R H, Keating G M, Zurek R W, et al. Application of acclerometer data to atmospheric modeling during Mars aerobraking operations[J]. Journal of Spacecraft & Rockets, 2007, 44(6): 1172-1179.

[10] Prince J L, Dec J A, Tolson R H. Autonomous aerobraking using thermal response surface analysis[J]. Journal of Spacecraft & Rockets, 2009, 46(2): 292-298.

[11] Kumar M, Tewari A. Trajectory and attitude simulation for aerocapture and aerobraking[J]. Journal of Spacecraft & Rockets, 2005, 42(4): 684-693.

[12] Johnson W R, Longuski J M, Lyons D T. Pitch control during autonomous aerobraking for near-term mars exploration[J]. Journal of Spacecraft & Rockets, 2003, 40(3): 371-379.

[13] Tolson R H, Bemis E, Zaleski K, et al. Atmospheric modeling using accelerometer data during Mars reconnaissance orbiter aerobraking operations[J]. Journal of Spacecraft & Rockets, 2008, 45(3): 511-518.

[14] Dec J. Probabilistic thermal analysis during Mars reconnaissance orbiter aerobraking[C]//Proceedings of 45th AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2007-1214, 2007.

[15] Smith J C, Bell J L. 2001 Mars odyssey aerobraking[J]. Journal of Spacecraft & Rockets, 2005, 42(3): 406-415.

[16] Prince J L, Striepe S A. NASA langley simulation capabilities for the Mars reconnaissance orbiter[R]. American Astronautical Society, 2005.

[17] Graf J E, Zurek R W, Eisen H J, et al. The Mars reconnaissance orbiter mission[C]//Proceedings of Aerospace Conference, 2005.

[18] Tolson R H, Dwyer A M, Hanna J L, et al. Application of accelerometer data to Mars odyssey aerobraking and atmospheric modeling[J]. Journal of Spacecraft & Rockets, 2015, 42(3): 435-443.

[19] Lyons D. Aerobraking automation options[J]. Advances in the Astronautical Sciences, 2001， 109(2): 1231-1246.

[20] Justus C, Johnson D. Mars global reference atmospheric model 2001 version (Mars-GRAM 2001): users guide[R].NASA TM-2001-210961, 2001.

[21] Johnson W R, Longuski J M, Lyons D T. Nondimensional analysis of reaction-wheel control for aerobraking[J]. Journal of Guidance Control & Dynamics, 2003, 26(6): 861-868.

[22] Hanna J L, Tolson R H. Approaches to autonomous aerobraking at Mars[J]. Journal of the Astronautical Sciences, 2002, 50(2): 173-189.

[23] Dec J, Gasbarre J, George B. Thermal analysis and correlation of the mars odyssey spacecraft′s solar array during aerobraking operations[C]//Proceedings of Astrodynamics Specialist Conference, Monterey, AIAA 2002-4536, 2002.

[24] Johnson M A, Willcockson W H. Mars odyssey aerobraking: the first step towards autonomous aerobraking operations[C]//Proceedings of IEEE Aerospace Conference, 2003.

[25] Coustenis A, Salama A, Schulz B, et al. Titan’s atmosphere from ISO mid-infrared spectroscopy[J]. Icarus, 2003, 161(2): 383-403.

[26] Mueller-Wodarg I C F.The application of general circulation models to the atmospheres of terrestrial-type moons of the giant planets[C]// Proceedings of Atmospheres in the Solar System: Comparative Aeronomy, 2002: 307.

[27] Justus C G, Duvall A, Johnson D L. Mars-GRAM validation with Mars global surveyor data[J]. Advances in Space Research, 2004, 34(8): 1673-1676.

[28] Justus C G, James B F, Bougher S W, et al. Mars-GRAM 2000: a Mars atmospheric model for engineering applications[J]. Advances in Space Research, 2002, 29(2): 193-202.

[29] Lockwood M K. Titan aerocapture systems analysis[C]//Proceedings of AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA 2003-4799, 2003.

[30] Lockwood M K. Neptune aerocapture systems analysis[C]//Proceedings of AIAA Atmospheric Flight Mechanics Conference and Exhibit, AIAA 2004-4951, 2004.

[31] Prince J L H, Powell R W, Dan M. Autonomous aerobraking: a design, development, and feasibility study[R]. NASA Langley Research Center, 2011.

Effect of Mars rarefied atmospheric dynamic error during aerobraking

FANG Baodong1,2,3, WU Meiping1, ZHANG Wei2,3

(1. College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China;2. Shanghai Institute of Satellite Engineer, Shanghai 200240, China;3. Shanghai Key Laboratory of Deep Space Exploration Technology, Shanghai 200240, China)

Aimed at the problem which Mars can rarefy atmospheric dynamic errors that caused by seasonal variations and diurnal changes during Mars areobraking, the orbital dynamic equation including aerodynamic force was established. Through the research of aerodynamic parameter calculation method applied to rarefied flow, the effect of dynamic errors on aerodynamic force and aerobrake result was analyzed. In consideration of the application in Mars exploration, the characteristics of aerodynamic and orbit during Mars aerobraking were simulated under the condition that the atmospheric dynamic errors exist. To assure the safety of spacecraft and the aerobraking duration, the corridor of aerobraking and the requirement of navigation were proposed. The result can be a reference for the aerobraking implementation of future Chinese Mars exploration.

Mars exploration; aerodynamic model; aerobraking; dynamic error

10.11887/j.cn.201605011

http://journal.nudt.edu.cn

2015-05-02

国家重点基础研究发展计划资助项目(2014CB744200)；上海市深空探测技术重点实验室资助项目(13dz2260100)

方宝东(1978—)，男，上海人，博士研究生，E-mail：fangbd@126.com；吴美平(通信作者)，男，教授，博士，博士生导师，E-mail：wumeiping@nudt.edu.cn

V488

A

1001-2486(2016)05-064-08